严寒地区铁路路基冻融沉降数值模拟研究

2013-01-16李东升

铁道标准设计 2013年12期

赵欢,李东升

(1.陕西铁路工程职业技术学院,陕西渭南 714000； 2.石家庄铁道大学土木工程学院, 石家庄 050043)

1 概况

某铁路客运专线地处我国严寒地区，年平均气温-12.4～10.9 ℃，极端最高温度39.8 ℃，极端最低气温达-40 ℃，最大积雪厚度30 cm，最大季节冻土深度达205 cm，冬季寒冷而漫长，每年从10月底开始冻结，翌年5～6月全部融化，沿线穿越软土、季节性冻土等地区，地质情况复杂。在高速车辆冲击荷载以及季节性冻土热融沉降和冻胀变形的长期作用下，路基的沉降变形是不可避免的，故建立路基冻融循环和列车动荷载耦合作用下的路基沉降模型，对路基沉降进行长期预测，具有重要的工程意义。

2 模型的建立

本文在线路上选取DK503+580路基典型断面进行数值模拟研究，模型建立如下。

(1)断面情况，见表1。

(2)轨道板，0.3 m厚；路基填筑材料层：①上层级配碎石和中粗砂，0.6 m厚；②下层非冻胀土和A、B组填料2.4 m厚。为了方便计算，这里把路基填筑部分的材料简化为填土3 m一层材料。

(3)地基土可分为2层：①上层为粉黏土，厚度在3 m左右；②下层为砂土，厚度大于20 m。

表1 某客运专线DK503+580路基断面情况

(4)可影响范围：纵向从天然地表向下延伸20 m，横向从路堤边界向左右各延伸10 m。

(5)网格划分：沿铁路纵向取50 m做为分析单元，50 m内共分成20份网格。

建立的模型见图1。

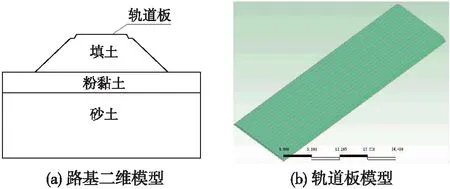
图1 路基模型

3 介质参数的选取

根据工程实况，可以把一个冻融循环下的路基冻融状态划分为如下几个阶段：

(1)冻结时间设定为11月15日至12月15日，该过程按变温冻结过程计算，温度变化范围-5～6 ℃；

(2)从12月15日至次年3月15日，该过程按恒温-4℃冻结过程计算；

(3)从次年3月15日至次年4月15日，该过程按变温融化过程计算，温度变化范围-4～12 ℃；

(4)从次年4月15日至次年5月15日，该过程按恒温12℃融化过程计算；

(5)从次年5月15日至次年11月15日，认为土体处于未冻结状态。

实际上路基土体的物理力学性质随温度的变化而变化，这里为了计算方便，作如下假设。

(1)在一个冻融循环内，每个阶段内的路基土体物理力学性质是不变的，即变温冻结、恒温冻结、变温融化、恒温融化和未冻结5个阶段各对应不同的土体物理力学性质不变，这是基于每个阶段温度的变化不是太大，故对土体力学性质的影响不太明显的基础上作出的假设。

(2)根据实际工程路基地温的监测数据[3]，在地基土体中，由于监测数据表明冻深不超过3 m，故受冻融影响的主要是地基粉黏土部分，从而可以认为砂土的材料参数在模拟过程中保持恒定，见表2。

(3)路堤部分简化为一种材料即填土。填土和地基粉黏土都受冻融的影响，根据前面对一个冻融循阶段的划分可知，两种土体在每个冻融循环过程中都要经历5个阶段，这5个阶段分别为：变温冻结、温恒冻结、变温融化、恒温融化和未冻结。在不同的阶段土体的力学参数是不一样的，故每一个冻融循环下土体力学参数也是不一样的，从而地基土体的力学参数要依据每个阶段每个冻融循环来确定，具体过程如下。

表2 砂土的力学参数

①首先确定初始冻融循环每个阶段的材料力学参数。根据相关试验数据[1]，初始冻融循环的不同阶段填土和粉黏土的力学参数见表3和表4。

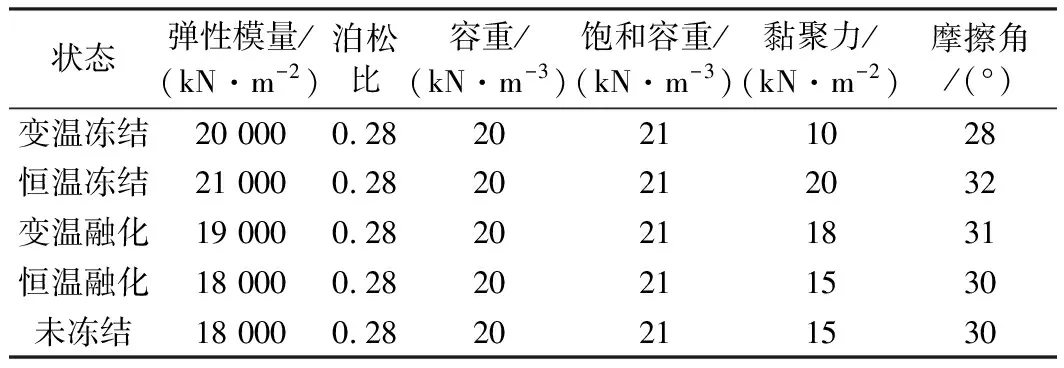
表3 初始冻融循环填土的力学参数特征值

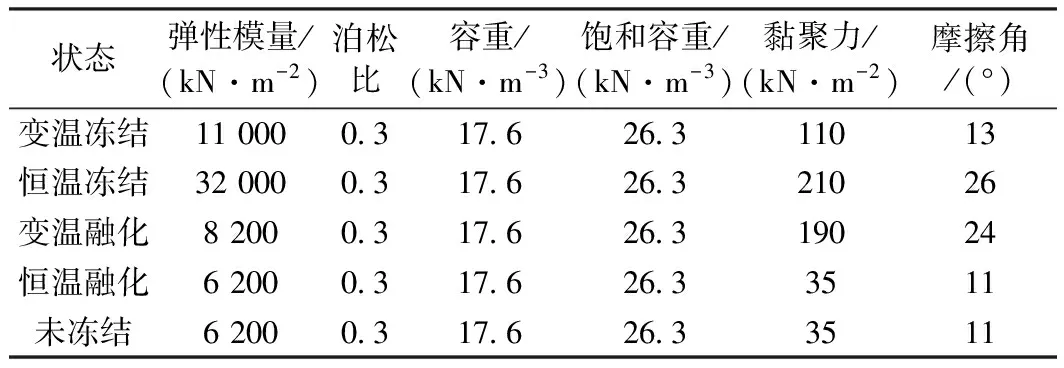
表4 初始冻融循环粉黏土的力学参数特征值

②在数值计算过程所输入的参数按照冻融循环中每个阶段来确定，即以第1个阶段(变温冻结)的数值计算结果作为第2个阶段计算的材料特征值，依次类推就能得出填土和粉黏土在各个冻融期间的材料特征值。

在模型定义的约束条件下有

(1)

式中σi——第i阶段的初始轴向应力值；

εi——第i阶段地基土初始轴向应变；

λi、ζ——受围压、含水量影响参数，分别取1.4和0.3；

A1、B1——含水量影响参数，分别取1.85和1.97。

如果不考虑蒸发因素，则土体中含水量在路基的沉降过程中不发生变化，故式(1)中的参数ζ，A1，B1在模拟中取定值，但λi是变化的，因为围压不固定，故第i+1阶段的λi+1可由式(2)变形得到

(2)

式中，σi+1为第i+1阶段初始轴向应力；εi+1为第i+1阶段初始轴向应变。它们分别为第i阶段末的应力应变值，从数值模拟中得出。

各种材料特征值确定的具体过程如下。

①泊松比、容重和饱和容重在冻融循环中取定值，分别为0.3、17.6 kN/m和26.3 kN/m；

②变形模量的确定：根据式(1)和式(2)得出每个阶段的初始应力、应变值，然后利用公式E=σ/ε就可以计算出变形模量。

③内摩擦角和黏聚力的确定：在式(1)中，将σ看作主应力差，在每个阶段中选取3个应变值，其中2个应变值分别为该阶段的初始应变和结束应变，另外一个应变值处于两者之间的任意一个值，把3个应变值代入到式(1)中就可以计算出相对应的主应力差，有了3个主应力差值就可以绘制出摩尔库仑圆，通过摩尔库仑圆的包络线就能得到该阶段土体的内摩擦角和黏聚力。

因为Midas软件只接受离散点的材料特征参数，对函数形式的材料特征值尚无相应的输入程序，故本次模拟中对参数特征值按阶段逐步进行输入。

4 沉降量的计算分析

4.1 列车动荷载下的竖向位移

根据文献[2]，高速铁路动荷载可按下式计算

Pd=Ps(1+0.003ν)(3)

式中Ps——活载，取为1 100 kN；

ν——列车速度，取线路设计速度350 km/h。

所以高速铁路动载为

Pd=1 100×(1+0.003×350)=2 255 kN(4)

假定动荷载在基础板上均匀分布，路基板宽度3.5 m，荷载纵向作用深度为10 m，扩散系数取0.96，则作用在路基面上的动应力为

qd=0.96×2 255/35=61.6 kPa(5)

故列车动荷载值取为61.8 kPa，根据Y225K型旅客列车的各轴间距(同节列车轴间距18 m，相邻两节列车轴间距7.5 m)，列车运行速度按设计值350 km/h计算，得到列车平均轴频率为28 Hz。

根据文献[2]，振动波型模型见公式

σd=40[1-cos(2π×20)t](6)

根据上述的材料参数、荷载输入以及阻尼，利用Midas计算出列车经过一次对应的Z方向(竖向)位移，分析结果见图2～图7。

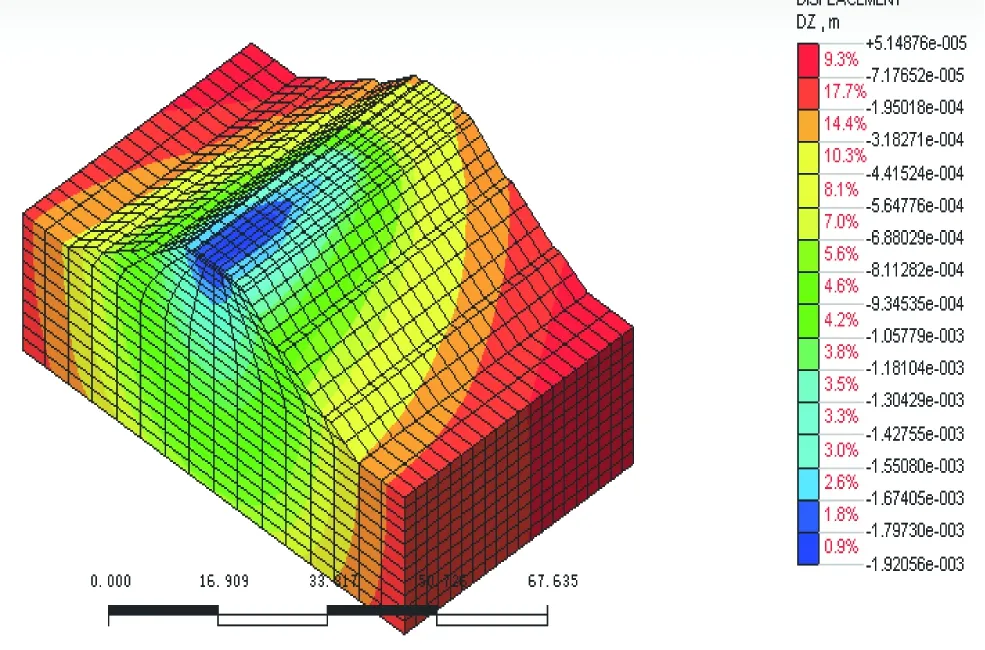
图2 列车进入0.7 s时的Z方向位移

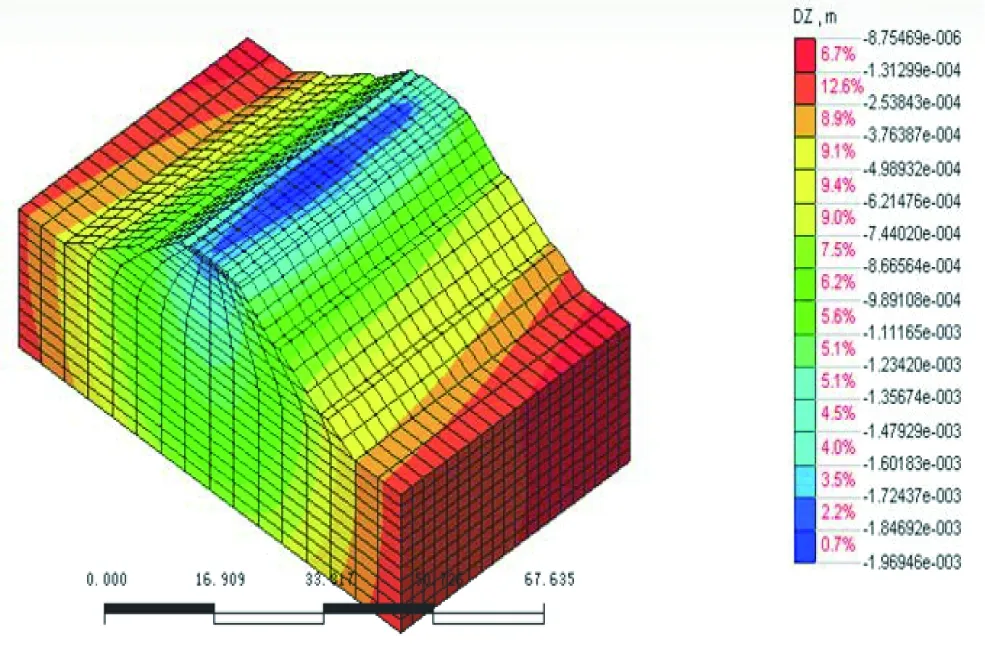
图3 列车进入1.0 s时的Z方向位移

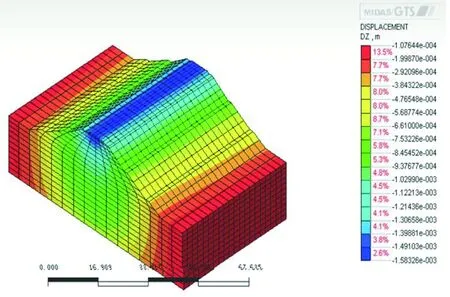
图4 列车进入1.7 s时的Z方向位移

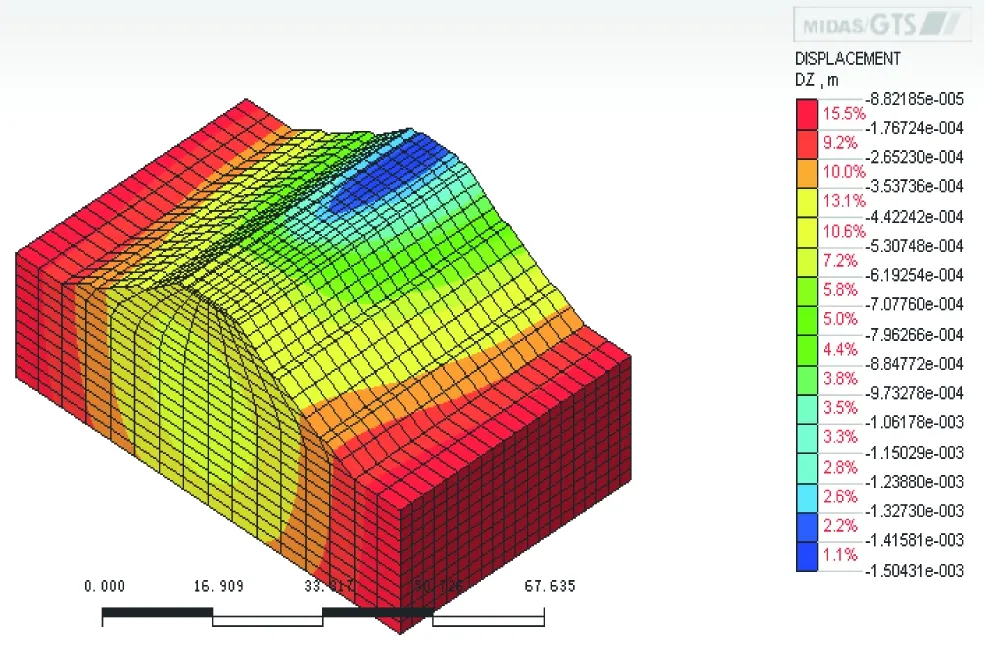
图5 列车进入2.4 s时的Z方向位移

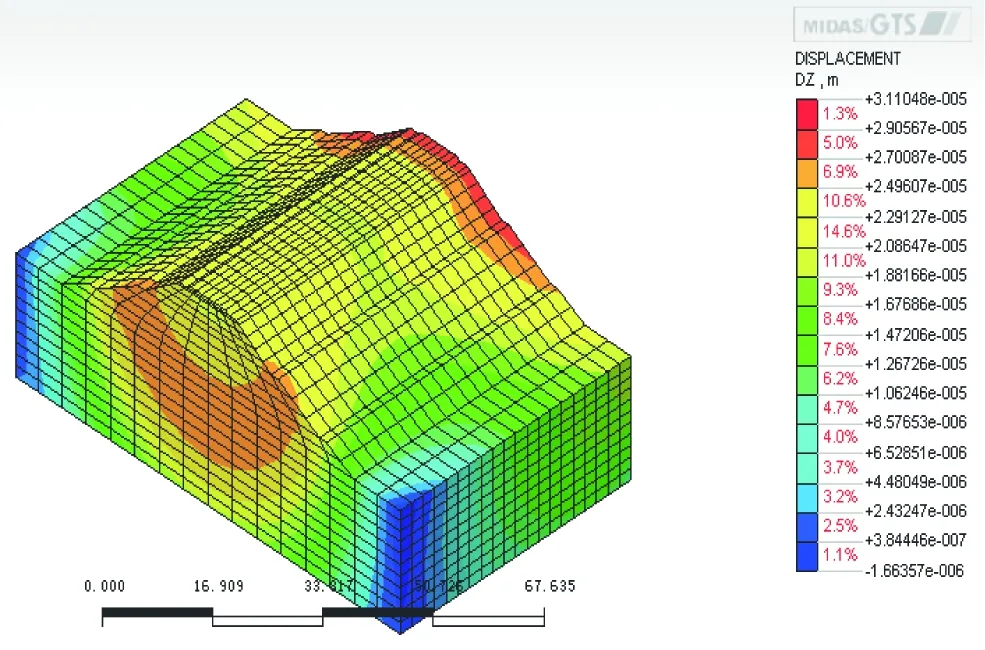
图6 列车进入3.5 s时的Z方向位移

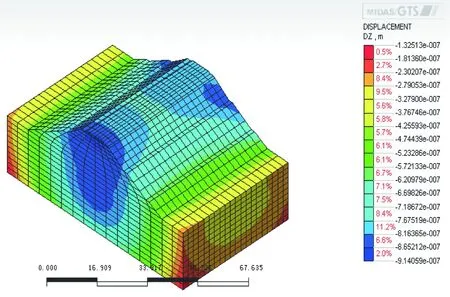
图7 列车进入5.0 s时的Z方向位移

4.2 沉降量计算

根据计算模型设定长度(50 m)及Y225K型旅客列车轴间距(同节列车轴间距18 m，相邻两节列车轴间距7.5 m，共25.5 m)可以将上述计算结果看作是由2次振动产生，据此，按如下步骤计算动载与冻融循环耦合下地基沉降量。

(1)将一个冻融循环过程按变温冻结、恒温冻结、变温融化、恒温融化和未冻结划分为5个阶段，根据前面温度变化时间设定，各阶段对应的时间为：

①变温冻结阶段历时30 d；

②恒温冻结阶段历时90 d；

③变温融化阶段历时30 d；

④恒温融化阶段历时30 d；

⑤未冻结阶段历时为185 d。

假设每天通车10次，结合列车的轴频率28 Hz，则可以确定振次为280次/d，每个阶段中以10 d为一个计算周期，则每个计算周期的振次为2 800次。根据实验室里动三轴试验结果可以知道[5]：当围压较大时，可以认为轴向应变值与振动次数成正比。故每个计算周期中的累积沉降量为该周期中第一次振动所产生的残余位移值与周期内振动次数的乘积。

(2)根据第i个计算阶段的累积沉降量来计算第i+1个计算阶段的材料力学参数特征值。本文具体列出模拟5次冻融循环，其相对应的具体材料力学参数特征值见表5、表6。

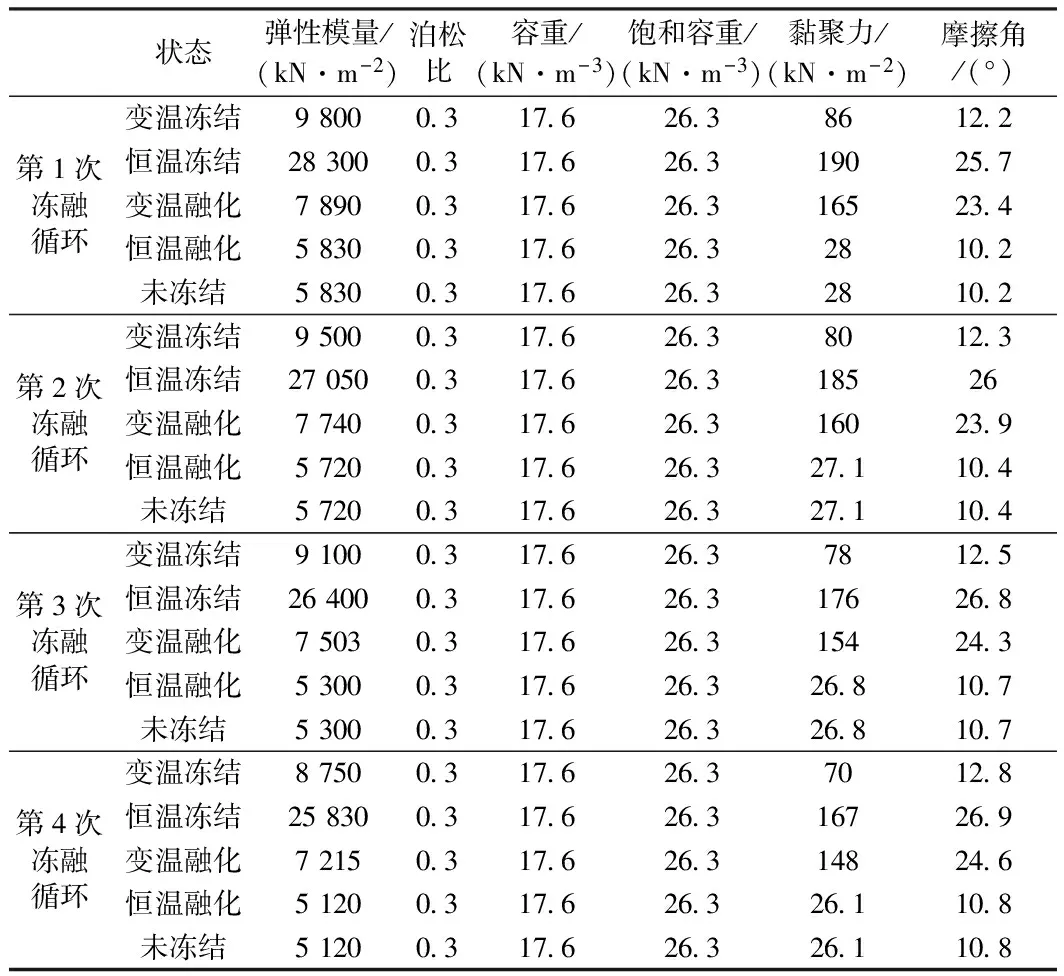
表5 粉黏土的力学参数特征值

从上面的材料力学参数可以看出，路堤填土的防冻性能较好，冻结期和融化期内的力学性质变化很小；地基粉黏土容易受冻融作用的影响，冻结状态和融化状态的力学性质相差很大，须采取一定的地基加固措施。在冻融循环的影响下，可以发现材料的变形模量和黏聚力是减小的，但摩擦角是增大的。

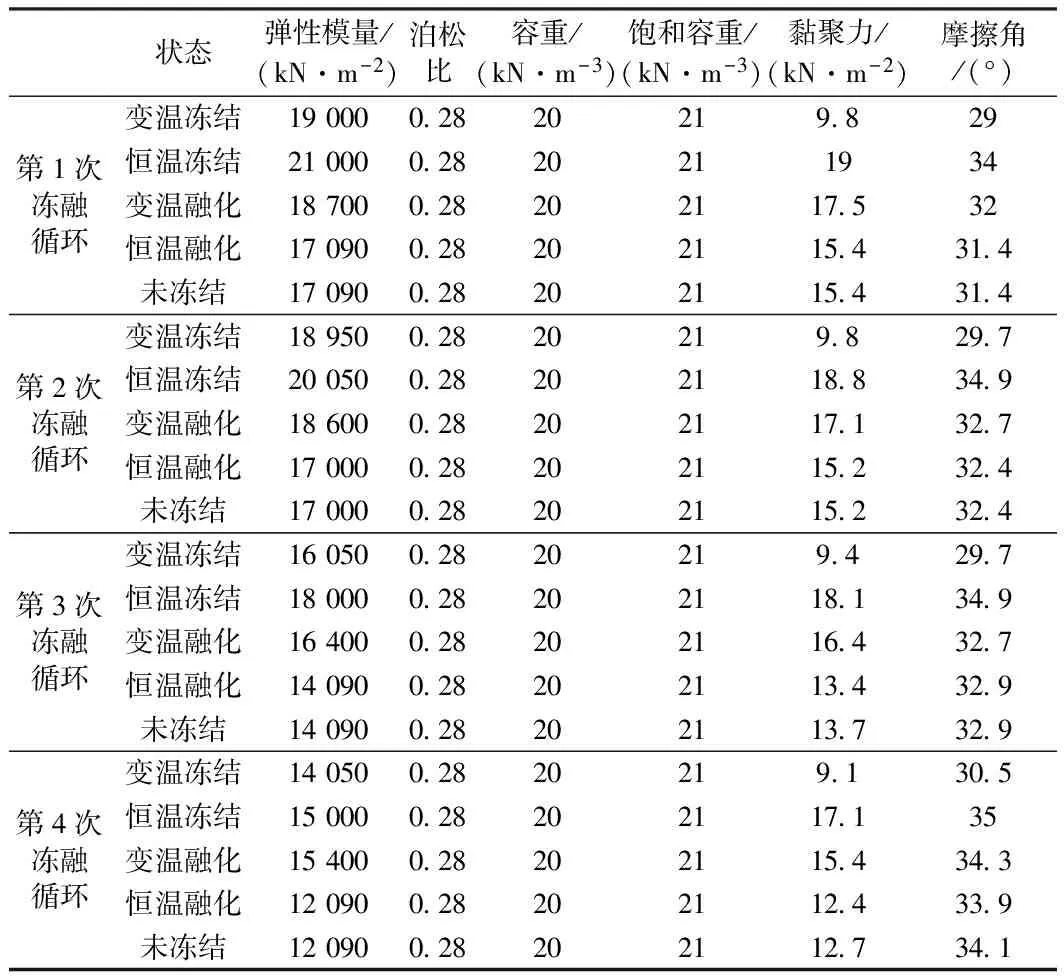
表6 填土的力学参数特征值

(3)根据确定的材料力学参数特征值，利用Midas计算第i+1计算周期中第1次振动所产生的沉降量。然后利用其残余沉降值乘以这个周期的振次，就得到了这个周期的沉降量，进而可以得到该阶段沉降量和这个冻融循环的沉降量。

(4)重复(2)～(3)步可计算出多次冻融循环下高速铁路地基的沉降量。

根据上述计算步骤，10次冻融循环作用下路基累积沉降值的计算结果如图8所示。

图8 10次冻融循环作用下路基累积沉降曲线

从模拟计算结果中可以看出，在前3个冻融循环过程中，路基沉降量增长缓慢，累积沉降值为2.08 mm，这说明所选用的材料已经消除了冻融所造成的竖向位移，其增长的数值源于粉黏土在动荷载作用下不可避免的沉降性，须采取一定工程措施。当超过3个冻融循环时，路基沉降量明显增长，原因在于冻融造成的直接变形虽然已经被消除，但冻融作用的强烈风化作用却依然存在，随着冻融循环次数的增加，填筑材料的风化效果逐渐显现，导致结构发生变化，结构强度降低，路基沉降量明显增长，到达第5个冻融循环结束时，累积沉降值已经达到7.6 mm。为了避免出现或推迟该现象的出现，应该做好路基的防水准备，随着时间的推移，累积沉降值逐渐趋于一稳定状态。