导航卫星仿真信号控制精度测试与评定

刘 岩，姚志成，范志良，管洪杰，张 辉

(西安灞桥高科技研究所卫星导航实验室，陕西西安710025)

0 引言

随着卫星导航仿真技术的成熟，卫星导航仿真不仅仅用于卫星导航接收机的研发与测试，一些科研机构开始研究通过构建卫星/惯性组合导航、制导控制系统的闭环半实物仿真系统，以验证无人飞行器、舰船等所搭载控制系统的实际工作性能，其基本原理为:以仿真计算机为控制中心，根据导航/制导计算机中的信息和相应物理模型，实时仿真计算控制系统载体的位置、速率等质心运动参数，而后产生2路信号:① 送给实物/数字平台模拟运动状态产生惯性导航信号;②传递给卫星导航仿真器来模拟产生载体运动过程中的卫星信号并由卫星导航接收机接收该信号，惯性装置的测量数据和接收机数据共同传递给导航/制导计算机产生相应制导信息，再传递给仿真计算机，为下一轨迹点的计算做好准备，从而形成一个闭环系统。

无论是弹载接收机性能的全面评估，还是组合导航系统闭环仿真验证，都需要高性能GNSS信号仿真器。由此可见，对仿真器信号指标的测试与评定技术研究是不可缺少的。

1 仿真器信号控制精度相关指标

卫星导航仿真精度包括2部分:①数学仿真精度［1］，主要指数学模型构建准确度、数值计算等;②仿真信号控制精度［2］，主要指数学仿真后信号生成的控制精度。由于对实际物理模型构建各式各样，而且不同的模型对处理实际问题的侧重点不一致，很难从一个统一的方向对其进行分析。

因此，仅研究仿真信号控制精度指标的测试，主要包括以下2个方面:

①仿真器信号合成精度测试。仿真器信号合成精度测试用来标定卫星导航仿真器的真实动态分辨率、精度和能够准确仿真的动态范围。动态分辨率和精度测试通常根据仿真器理论分析和实际需求，选取若干组动态参数控制信号合成，进行动态参数标定。而动态范围测试通常根据给出的仿真动态范围计算得到相应的延时与延时变化率的动态范围，然后设置仿真延时以相应延时和延时变化率的极值进行匀状态变化。在进行高阶动态特征测试时，为了保证对高阶动态特征积分的低阶动态特征不超过相应的动态范围，需要以一定时间间隔切换延时变化的方向。

②仿真器的闭环延时测试。仿真器闭环延时测试用于标定在控制系统闭环仿真中，从仿真器接收到数据开始，经过仿真计算，到信号合成输出该数据对应的仿真信号所需要的时间。若仿真器的延时超出或者不确定，造成导航系统信息与惯导信息的关系不匹配或不确定，这将导致控制系统综合得到的控制命令错误或不可预测，从而无法分析控制系统的组合效能。在控制系统闭环仿真过程中，获取每个闭环周期或者一部分闭环延时参数，通过统计分析出闭环延时的特性，为控制系统闭环仿真提供参数依据。

2 信号处理方法对比

2.1 仿真信号与卫星信号完好性测试的不同

卫星信号从外太空发射到地面，所经过的环境复杂多变，其信号的质量对最终的导航终端定位结果有相当的影响［3］，因此在地面对实际卫星信号质量监测十分重要，其主要目的是为了保证系统所有卫星连续可靠的工作，保障用户工作的安全性、完备性［4］。卫星信号质量的测试主要侧重在信号的品质上，如对导航信号的地面接收功率(带内功率)、频率(频谱、带宽等)等实时监测，也可对典型通信信号参数如功率谱密度、眼图、星座图和信号调制参数等进行实时监测、信号通路测试和群延时等。

相比较而言，仿真器输出信号一般通过屏蔽电缆直接输出至被测接收终端，或者通过广播天线近场发射，因此仿真的信号受外界影响很小。在仿真器中是需要通过对实际卫星信号的传播途径进行建模，转换为相应的控制量来产生接收机前端的卫星信号，因此对仿真器信号的测试应该侧重于信号产生的控制精度。

2.2 仿真信号与接收机信号处理方法的不同

仿真信号的指标测试必然需要对仿真信号的伪距、多普勒频移和载波相位等参数进行估计，虽然仿真卫星导航信号的组成、调制仿真与实际卫星导航信号相同，但是仿真卫星导航信号与实际卫星导航信号也有所区别，主要表现为:

①实时性要求。接收机对信号处理［5-7］要对卫星导航信号进行实时跟踪，提取有用信息，并解算出定位结果;而仿真器信号测试在于对仿真信号产生过程中的各个状态量给出一个准确的量值或统计值，不需要实时解算出定位信息，可以进行离线处理。因此，仿真信号测试中可以使用这些无法满足接收机/导航终端实时性要求的方法/算法。

②对象功率。接收机捕获的信号来自与卫星发送的信号，终端接收的信号功率很弱，一般在-150 dBW左右［8］，其有用信号湮没在噪声中。在对该信号处理过程中，必须通过相对长时间的相干累加，才能将从噪声中分离出有用信号。

在仿真卫星导航信号测试过程中，仿真信号一般通过射频电缆直接与测试采集设备连接。仿真卫星导航信号中的噪声主要来源于3个方面［9］:有意仿真的噪声，根据相应的噪声模型和产生方法，人为添加到仿真信号中，用于调整仿真信号的信噪比(另一种做法是调整仿真信号的功率);数字信号合成方法本身所引入的噪声，主要来源于相位截短和幅度截短引入的量化噪声;仿真信号模拟和射频电路的热噪声，包括数模转换器、本振电路、混频电路、衰减电路和滤波电路的综合噪声，可以根据电路的热噪声温度，利用波尔兹曼常数计算得到。

③导航数据调制导航信号捕获算法和跟踪算法中，观测数据块中导航数据位的状态翻转会使相关运算结果与非Costa环路鉴别器输出，相对于无翻转时衰减kc倍(如下式所示，T为相关或相干累加序列时间长度，tDT为相对序列起始时刻的导航数据位翻转时刻)［10］。

当导航数据翻转时刻越接近相干积分时间段中值时，相干积分结果的衰减越大。

通道导航数据调制的开关一般作为仿真器的一项基本功能，而且易于实现。在仿真信号精度测试时，可以关闭导航数据调制(等效为调制的导航数据位全部相同)。测距码整周模糊度可以用仿真器输出的同步时标来确定，无需导航数据流辅助，从而避免了导航数据位翻转引起的相干累加。因此，对导航数据位翻转敏感的卫星导航信号处理方法可以用在仿真信号精度测试中。

④时基同步性。在仿真卫星导航信号测试中，卫星导航仿真器与测试采集设备可以共用同一基准时钟，可以保证仿真信号精度分析中，仿真和测试采集时基差异所导致的误差最小。此时，仿真和测试采集的时基差异主要为2路时钟传递通路的不一致性:其中确定部分来源于2通路长度的差异，可以通过仿真器输出的同步时标剥离这部分误差的影响;随机部分来源于2通路上不同的热噪声，一般将2通路上热噪声之差视为采集噪声的一部分，在算法误差分析中给出时钟通路噪声与其他噪声的综合估计。

3 总体设计方案

通过研究仿真信号动态与闭环延时指标测试技术，提出一套完整的测试方法，总体工作思路如图1所示。

图1 总体工作思路

3.1 高阶鉴频器模型

在导航终端信号处理中，为了提高载波频率估计分辨率，需要利用估计的测距码初相产生的本地测距码序列，对观测信号中的测距码序列进行解调，然后通过鉴频器进行若干次频率牵引，获得较为准确的频率估计结果。通常所用的鉴频器有叉积型(Cross)、符号判别叉积型(Sign Cross)和反正切(Atan2)型3种，鉴频特性如图2所示。

图2 常用鉴频器的鉴别特性

Atan2鉴频器是一个4像限反正切鉴别器，在高信噪比和低信噪比时均是频率偏差的最大似然估计，且斜率与信号幅度无关［11］。从图2中也可以看出在一个相关周期内(1 ms)，输出和输入基本呈线性关系，因此以Atan2鉴频器为基础，构建高阶鉴频器模型。

Atan2鉴频器算法为:

式中，IPS1，QPS1为本地复现载波正交2路信号;IPS2，QPS2为接收的载波正交2路信号;t2-t1为载波信号采样时间间隔。为了在一个周期内构建高阶模型，将每个周期分成3段，每段时间间隔为T。设选取码延时和多普勒频移的零阶、一阶、二阶量作为系统状态量，记为:

rp为码速率;fRF为射频频率。对上式进行离散化，若采样周期为T，可得

3.2 模型分析方法的选择

卡尔曼滤波器是一种线性无偏差递推滤波器，作为一种最优估计，被广泛应用于各种动态数据处理中，设计方法也简单易行。它有以下几个显著的特点［12］:① 用状态空间来描述数学公式;②具有递归结构的有限维线性离散时间系统，很适合用数字计算机实现，而且可以不加修改地应用到平稳和非平稳环境;③从随机状态空间导出的线性动态系统状态的最小均方估计。状态的每次更新估计都是由前一次估计和新的输入数据计算得到，所以只需要存储前一次的估计。因此卡尔曼滤波算法在计算上比直接根据滤波过程中每一步所有过去数据进行估值的方法更有效。

模型误差的统计性质是时变的，噪声是相关的。若量测噪声和状态噪声的统计性质不够了解，一方面会导致滤波结果不精确或者把偏差加到状态估计里面去;另一方面将导致滤波发散［13］。

3.3 状态量估计算法

状态量估计算法原理框图如图3示。

图3 状态量估计算法原理

第1步，将采集信号和高阶信号合成器产生的本地信号同时输入相关积分器，获取I、Q之路信息;

第2步，IQ两路信号输入信号状态估计器组，对信号进行处理，获取信号的状态粗估计量;

第3步，状态粗估计量输入到滤波器得到信号状态的最优估计值;

第4步，通过信号的状态最优估计值合成本地信号用于下一步的信号相关。

4 实验方案

在研究过程中，研究方案采用系统建模→理论计算→数字仿真→测试系统搭建→数据采集分析4个步骤进行，对结果进行有效验证。

4.1 仿真器信号合成精度测试实验方案

通过仿真器控制软件，设置仿真器工作在单一通道输出模式，分别设置仿真伪距变化率、伪距二阶变化率、伪距三阶变化率为+0.01m/s、+0.01m/s2、+0.01m/s3运行一段时间;利用高精度示波器对仿真信号进行依次采样并存储。使用本文提出的方法，对采样的数据进行处理，获取仿真器动态分辨率和精度。多次重复以上实验，得出该指标的统计信息。

4.2 闭环延时测试实验方案

实验以运载闭环控制系统为实验平台，如图4所示。

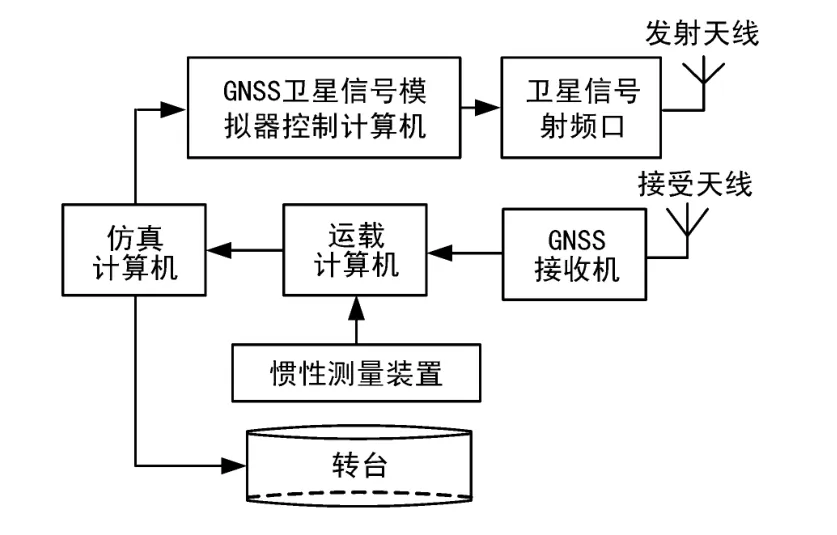
图4 闭环延时测试实验原理

以仿真计算机为控制中心，根据计算机中的信息，实时模拟计算用户的轨迹点，产生2路信号:一路信号控制三轴转台的转动控制惯性装置模拟运动状态;另一路传递给GNSS卫星信号仿真器来模拟产生载体运动过程中的卫星信号并通过天线发射出去，然后由GNSS接收机接收该信号。惯性装置的测量数据和GNSS接收机的数据共同传递给运载计算机，最终由运载计算机将其信息传递给仿真计算机，为下一轨迹点计算做准备，这样形成了一个闭环。

5 结束语

论文成果可应用到GNSS仿真器的指标测试，为运载控制系统半实物仿真和运载接收机测试评估提供相应的指标依据。更重要的是为运载接收机的动态功能测试提供了可行性，对运载接收机的性能给出一个全面、量化和可靠的评估依据，从而提高系统的可靠性和精度;另一方面，降低了载体运动过程的高动态导航卫星信号获取时的人力、物力上的消耗，并且保证了每次实验条件完全一致，有利于通过重复试验来定位所设计组合导航系统中存在的问题。

［1］ 赵军祥.高动态智能GPS卫星信号仿真器软件数学模型研究［D］.北京:北京航空航天大学博士学位论文，2003:11-14

［2］ 朱宇虹.高动态GPS卫星信号仿真器的研究与设计［D］.北京:北京航空航天大学博士学位论文，2004:8-13.

［3］ PHELTS R E，AKOS D M，ENGE P.Robust Signal Quality Monitoring and Detection of Evil Waveforms［C］∥Proceedings of the Institute of Navigation ION GPS.Salt Lake City:UT，2000:1 180-1 190.

［4］ CHRISTIE J R I，BENTLEY P B.GPS Signal Quality Monitoring System［C］∥ION GNSS 17th International Technical Meeting of the Satellite Division 2004.USA:SunDiego，2004(9):21-24.

［5］ 寇艳红.GNSS软件接收机与信号模拟系统研究［D］.北京:北京航空航天大学博士学位论文，2006:6-12.

［6］ HURD W J.High Dynamic Global Position System Receiver［P］.US:4578678，1986.

［7］ HINEDI S，STATMAN J I.High-Dynamic GPS Tracking［J］.NASA Publication，1988(5):89-113.

［8］ Navstar GPS Joint Program Office.Navstar GPS Space Segment/Navigation User Interfaces［R］.IS-GPS-200D，US Air Force:Rev D，2006(3):11-14.

［9］ DONG Lei.IF GPS Signal Simulator Development and Verification［D］.A Thesis of Master of Science，University of Calgary，Alberta，Canada，2003(11):25-29.

［10］ XU Guo-chang.GPS:Theory，Algorithms and Applications［M］.Berlin Germany:Spriner Verlag，2003:261-289.

［11］ KAPLAN E D，HEGARTY C J.Understanding GPS Principles and Applications 2nd Edition［M］.Boston/London:Artech House Inc，2006:1-9.

［12］宋迎春.动态定位中的卡尔曼滤波研究［D］.湖南:中南大学博士学位论文，2006:11-18.

［13］ TODA N F，SCHLEE F H，OBSHARSKY P.Regions of Kalman Filter Convergence for Several Autonomous Navigation modes［J］.AIAA Guidance，Control and Flight Dynamics Conf，Huntsville，1967(8):617-623.