裂缝影响下碾压混凝土拱坝整体安全度评价

(1.河海大学 水文水资源与水利工程科学国家重点实验室，江苏 南京，210098；2.河海大学 水资源高效利用与工程安全国家工程研究中心，江苏 南京，210098；3.河海大学 水利水电学院，江苏 南京，210098)

碾压混凝土坝综合了混凝土坝的安全性和土石坝的高效施工特性，但全断面通仓薄层碾压、连续快速上升的施工工艺，导致混凝土的水化热来不及散发，坝体在浇筑后一段时间内会达到很高的温度，坝体从施工期冷却到稳定温度场的过程中会产生较大的温度应力，碾压混凝土拱坝温度裂缝问题十分突出[1]。另外由于外荷载、地基不均匀沉降等造成的坝体裂缝也不容忽视[2]。拱坝作为一种经济且独有超载能力和应力自调节的坝型，坝体中裂缝的存在不仅使其外观变差，形成集中渗漏通道，更会破坏拱坝−地基系统的整体受力结构，改变系统原有的应力场和位移场，特别是径向贯穿性裂缝的存在，将直接减弱拱的作用，破坏拱坝的受力工作特点，裂缝进水后使得混凝土发生化学侵蚀，严重时将缩短拱坝健康服役寿命。刘耀儒等[3]结合小湾拱坝出现的拱向裂缝，研究了拱向裂缝对拱坝受力和稳定的影响，并得出小湾坝体拱向裂缝对坝体应力和整体稳定影响不大的结果；傅少君等[4]对小湾拱坝诱导底缝进行了研究，并且表明此缝对拱坝整体安全性影响较小。然而目前关于裂缝对拱坝整体安全性影响的研究还不够成熟，特别是径向贯穿性裂缝对拱坝整体安全性的影响研究则更少。因此，本文根据某碾压混凝土拱坝拱冠梁处径向贯穿性裂缝的实际情况，结合拱坝失稳破坏机理和整体安全度评价方法，建立三维数值仿真分析模型并进行非线性分析，研究有无裂缝情况下坝体的变位和应力状态，以及超载情况下拱坝−地基系统各部位的屈服情况，综合评价裂缝对该拱坝整体安全度的影响。

1 拱坝整体安全度分析方法

1.1 拱坝失稳破坏机理

拱坝−地基系统研究对象主要包括坝体、坝基岩体以及两者之间的接触面(建基面)，已有的研究成果表明[5−8]，其主要破坏机理有：(1) 坝肩岩体失稳破坏，如法国Malpasset拱坝；(2) 水库库岸滑坡，以意大利Vajont拱坝库岸大滑坡为典型代表；(3) 拱坝沿建基面的滑移；(4) 坝体强度破坏，地震、地基不均匀沉降等导致坝体局部应力超过混凝土的极限承载力；(5) 上滑失稳，以我国福建梅花拱坝溃决失事为代表，拱坝沿建基面或周边缝向上游滑动，致使拱圈的拱脚张开，拱坝中部或其他部分断裂导致突然破坏。

1.2 拱坝整体安全度评价

拱坝的破坏往往是上述多种不利因素共同作用的结果，其三向固定的空间高次超静定结构特点以及依靠两岸坝肩岩体维持稳定的受力工作特点，使得拱坝安全评价方法极为复杂。拱坝应力状态以受压为主，充分发挥了混凝土抗压能力强的特点，坝体的承载能力是相当大的。拱坝结构特点使其具有自动调整荷载分配的能力，坝体局部破坏不能代表整体的破坏，而是导致坝体及地基的应力重分配，系统安全状况也将随之会发生变化；另一方面，目前用于拱坝安全分析的坝体强度分析及拱座稳定分析方法，两者监控指标不一致导致对应的安全度必然不协调，而人们更加关心的是拱坝的整体安全度，特别是裂缝等造成坝体结构损伤的情况下，因此需对拱坝−地基系统进行整体安全度评价。

目前国内研究拱坝及地基系统整体安全度大多都是基于稳定性理论[7]，并取得了大量有意义的成果[9−12]。结合拱坝的受力工作原理，稳定性理论将拱坝的整体破坏归结为稳定性问题，并将拱坝的安全度作为衡量拱坝稳定安全性的指标。目前研究拱坝整体安全度的方法主要有超载法、强度储备法以及综合法[13]，通过超载或者降低材料强度，并利用收敛性判据或突变性判据[7]，判断拱坝-地基系统失稳时的极限平衡状态，此时超载的倍数或者材料降低的倍数即为拱坝−地基系统的整体安全度。超载法及强度储备法是建立在仿真分析的基础上，其应力场和位移场通过有限元求解所得，并且稳定分析过程中不需要事先假定屈服滑移面，而是通过变形的大小来自动搜索，比较符合实际情况。

2 仿真分析模型

某碾压混凝土双曲拱坝，最大坝高94.5 m，坝顶长252.3 m，坝顶宽6.0 m，坝底厚20.0 m。由于各种原因，该拱坝竣工前在拱冠梁剖面附近上下游面各发现1条裂缝，从建基面向上延伸48 m，且经过检测后确定该裂缝为上下游径向贯穿性裂缝。

根据实际情况模拟坝体结构、主要断层及裂缝等，建立有无裂缝2种三维有限元模型，运用非线性有限元分析方法，计算多组水位、温度等荷载作用下坝体应力及位移，结合超载情况，对比分析有无裂缝2种情况下，拱坝的应力及位移分布情况、结构屈服情况及超载能力，综合评价裂缝对该碾压混凝土拱坝整体安全性的影响。

2.1 计算模型的建立

三维非线性有限元计算范围的确定：以拱冠梁剖面为参考，坝体上游取1倍坝高，坝体下游取2倍坝高；以左右岸坝肩最突出处为参考，左右岸岩体各取1倍坝高；竖直方向在河床建基面以下取1倍坝高。根据地质资料，计算范围内包含F4和F5 2条断层，断层单元建模厚度为10 cm。模型以八结点六面体单元为主，局部采用六结点五面体单元，整体结点数及单元数分别为8 228和7 585，坝体的节点数和单元数分别为3 835和2 860；整体三维模型及结构面网格如图1所示。模型底面为三向固定约束，4个侧边界均为法向约束。

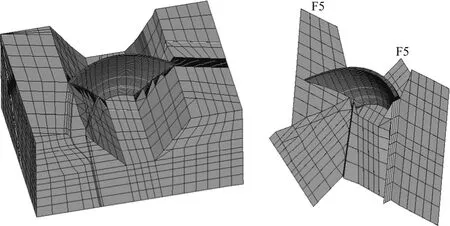
图1 整体三维模型及结构面Fig.1 Integral 3D model and main structural planes

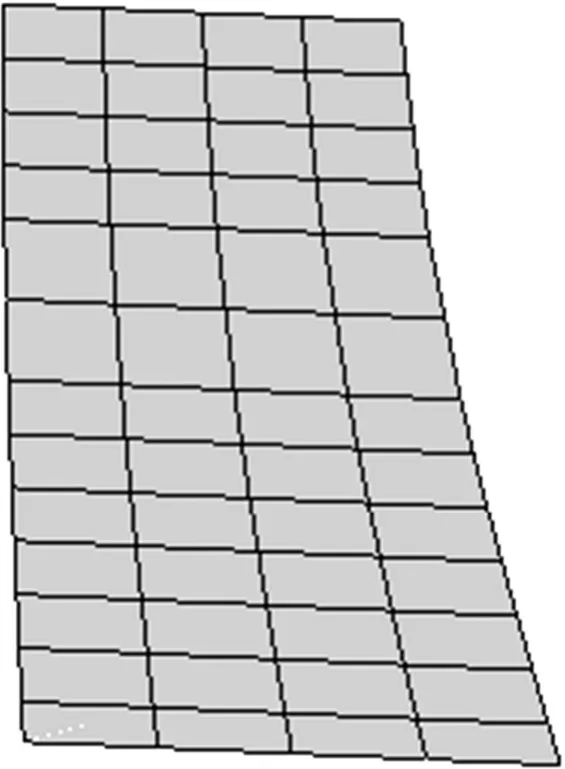
图2 裂缝单元网格Fig.2 Crack element meshes

坝体裂缝采用薄层单元模拟，并假定薄层单元可以100%的承受和传递压应力。裂缝单元建模厚度为1 cm，裂缝网格如图2所示。

2.2 材料参数

坝体混凝土、岩体及主要结构面物理力学性能见表 1。有限元分析时，裂缝单元的弹性模量取一较小值，以避免弹模为零时整体刚度奇异，本文中取裂缝单元的弹性模量为混凝土弹性模量的10%。

2.3 材料本构方程

非线性有限元分析通常认为岩体一般是非线性材料，简化分析时主要考虑构造软弱带的非线性影响，对坝体以及新鲜基岩仍按弹性体看待[14]。本文分析裂缝对坝体应力位移影响时，全部材料按线弹性分析；对整体超载安全度影响分析时分2种计算方法：第一种为将坝体采用线弹性，坝基岩体及断层采用基于Drucker-Prage屈服准则的弹塑性本构模型；另一种计算方法为坝体及坝基岩体全部采用基于Drucker-Prage屈服准则的弹塑性本构模型，研究超载时裂缝对坝体屈服情况的影响，分析该贯穿性裂缝加速坝体失稳的可能性。Drucker-Prage屈服准则用函数表示如下[15]：

表1 坝体及地基的物理力学性能Table 1 Physico-mechanical properties of dam and foundation

式中：I1和J2分别为应力张量的第一不变量和应力偏张量的第二不变量；α和K均为与材料的黏聚力c和内摩擦角φ有关的参数，且有

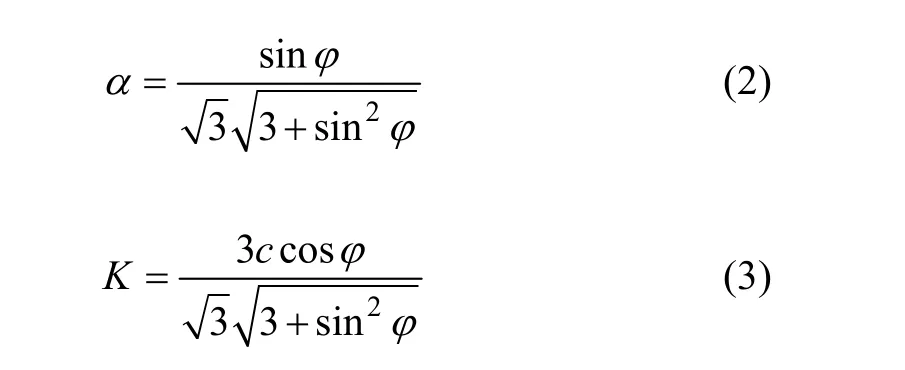
2.4 计算工况

根据该拱坝设计资料，计算工况及相应的荷载组合见表2，对于每种工况，分别计算有无裂缝2种模型下坝体的应力、位移及超载能力，对比分析裂缝的影响。

表2 计算工况及荷载组合Table 2 Calculating conditions and combination

3 计算成果分析

3.1 各工况应力位移分析

3种计算工况下，2种仿真模型各自坝体上下游面最大应力见表 3，坝体应力和位移分布规律总结如下：

(1) 无缝整体模型时，上下游面拱向应力和竖向应力基本呈对称分布，上游面拱向应力基本为压应力，最大压应力出现在坝体中部，坝体中下部建基面附近有拉应力分布，下游面拱向应力分布情况与上游面相反，最大拱向压应力出现在两岸坝肩，拉应力主要分布在坝址部位；上游面竖向应力也基本为压应力，最大压应力出现在坝体中部，建基面附近为拉应力分布区，下游面中上部大部分竖向应力为0 MPa，坝面下部及岸坡处为压应力分布区，最大压应力出现在坝址处。

(2) 仿真模拟裂缝情况下，坝体各部位应力分布情况与未开裂情况下基本相同，不同之处仅在于裂缝的存在使得裂缝端部附近出现了应力集中现象，进而导致裂缝附近局部应力增大。由于篇幅限制，仅列出了工况1坝体上游面应力分布情况，如图3和4所示。

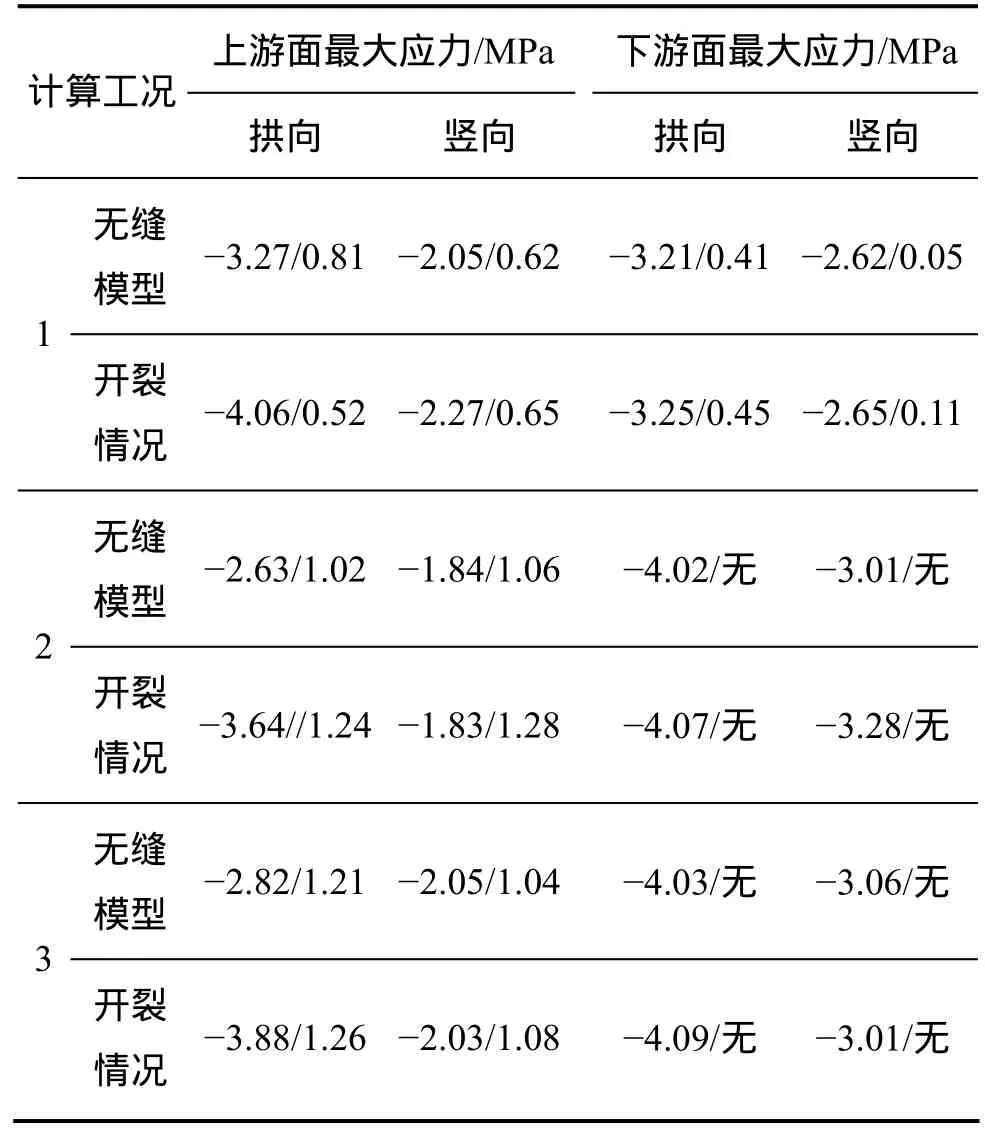
表3 拱坝上下游面最大应力Table 3 Maximum stresses of arch dam on upstream and downstream surface

(3) 该碾压混凝土坝贯穿性裂缝所在部位为拱冠梁剖面中部以下，有限元仿真分析结果表明：裂缝对拱坝位移场几乎没有影响，图5给出了工况1坝体下游面径向位移分布情况，其他工况规律类似。

有限元仿真分析结果表明，开裂情况下坝体位移和应力的分布规律及数值大小与无缝整体模型时基本相同，仅裂缝周边的应力分布规律和数值大小有一定的变化，因此可以初步判断该裂缝整体上对坝体结构影响较小。

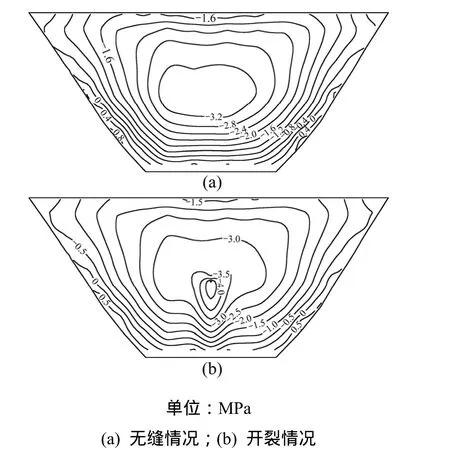
图3 工况1坝体上游面拱向应力Fig.3 Stress in arch direction on upstream surface in case 1

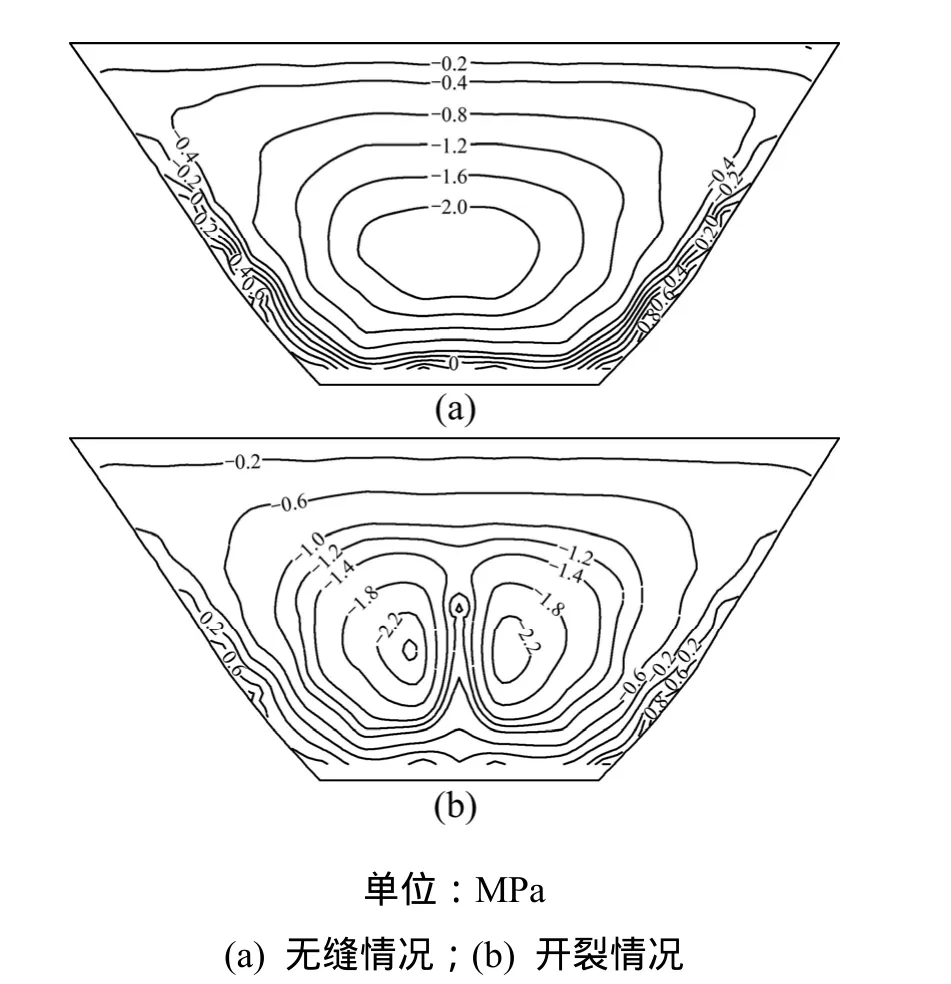
图4 工况1坝体上游面竖向应力Fig.4 Stress in arch direction of downstream surface in case 1

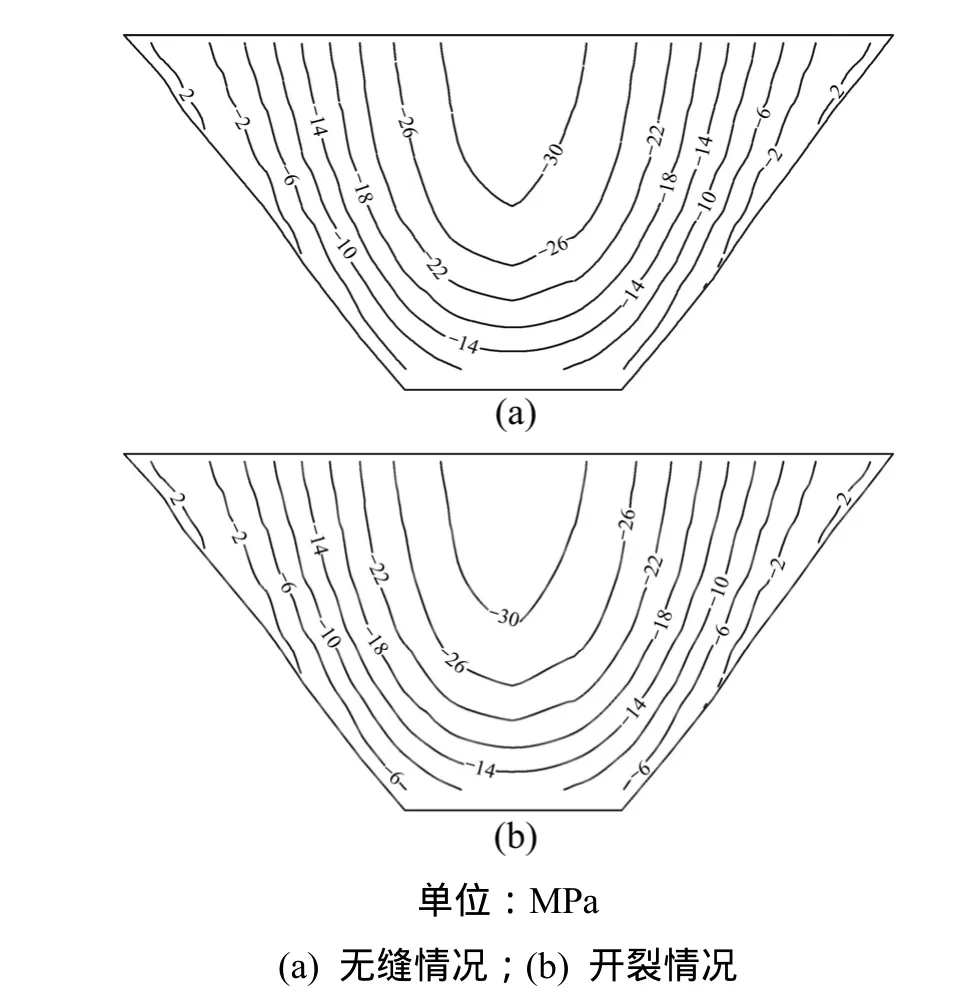
图5 工况1坝体下游面径向位移Fig.5 Radial-displacement of downstream surface in case1

3.2 整体安全度分析

结合该坝施工期出现裂缝的实际情况，整体安全度分析时，选用水溶重超载法分析裂缝对拱坝−地基系统整体安全度的影响。水溶重超载法是将水的容重提高为原来的Kp倍后(正常荷载时，Kp=1)，计算坝体和地基的应力场和位移场，观察坝体和建基面上某些关键点的位移、应力等变化情况，综合收敛性、位移突变及塑性屈服贯通情况，确定系统的整体安全度。

各工况应力位移分析结果已表明裂缝对该坝整体影响较小，因此，整体安全度分析时仅以工况1为例，在正常荷载作用后以 0.5倍的水溶重为间隔，开始超载上游水压直到计算结果不收敛，从模型的塑性屈服区分布和关键点的位移突变情况综合评价裂缝对拱坝整体安全度的影响。塑性屈服区判据认为在持续超载的情况下，坝体屈服区出现并不断扩展，进而出现屈服区的贯通，大坝形成机构运动，最后丧失承载能力。超载过程中，其他荷载保持不变。坝体位移典型点如图6所示，其中6号点位于拱冠梁剖面上游侧中部。

3.2.1 坝体线弹性分析结果

坝体采用线弹性，坝基材料采用基于 Drucker-Prage屈服准则的弹塑性本构模型。在超载系数由1.0，按照0.5倍的增量开始增大的过程中，当超载系数增大到12.5时，无缝整体模型的迭代计算不收敛；当超载系数增大到11.0时，开裂模型的迭代计算不收敛。从迭代计算的收敛性讲，裂缝对该拱坝−地基系统的整体安全度有一定影响，但影响不是特别显著。

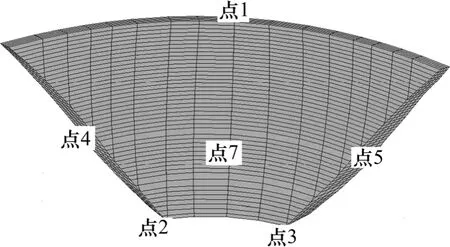
图6 位移典型点示意图Fig.6 Location of displacement typical points

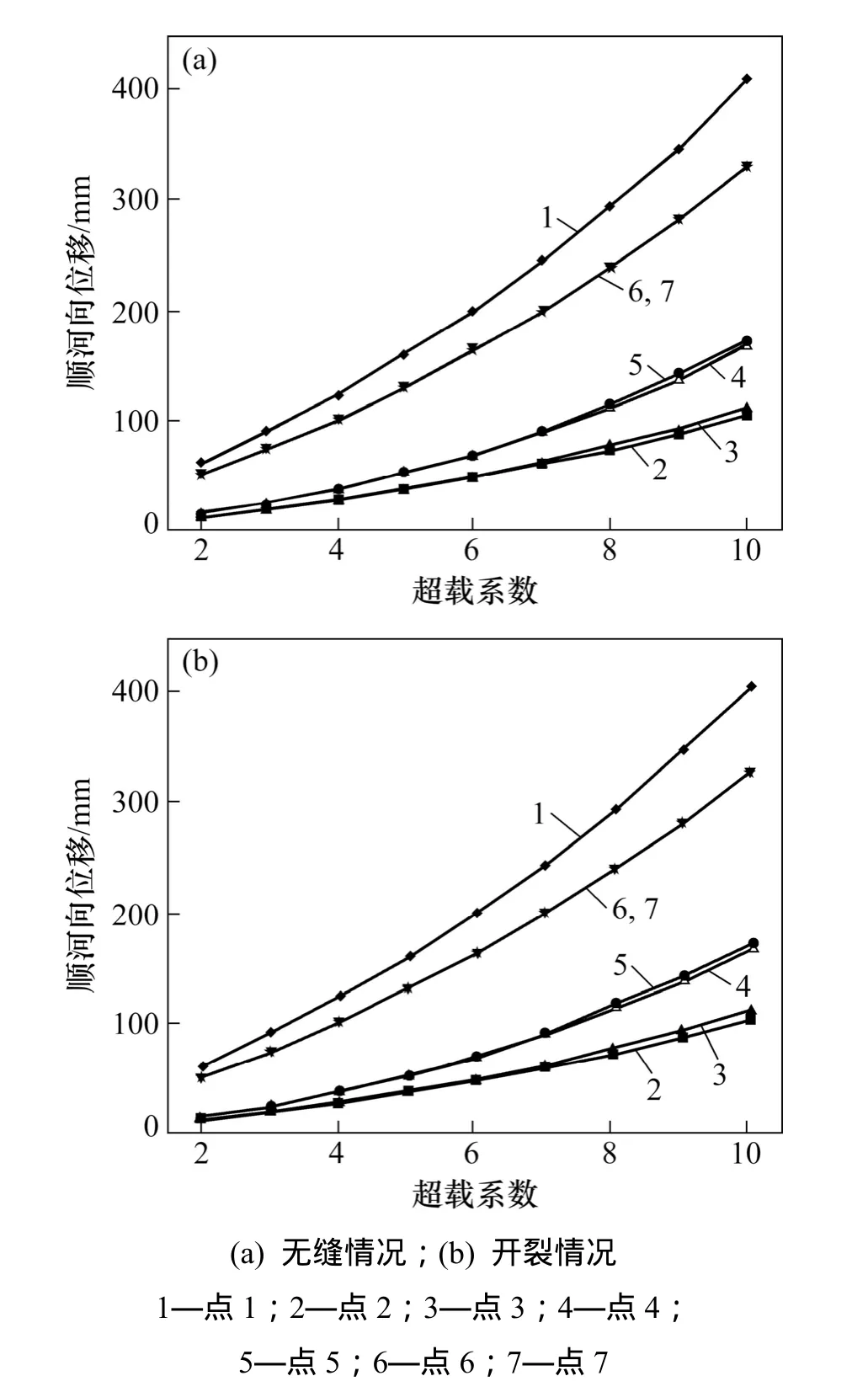
图7 坝体开裂情况下典型点顺河向位移与超载系数关系Fig.7 Relationships between displacement along river of typical points and overloading coefficient

超载分析时，无缝整体模型和开裂模型在相同超载系数下，2种模型计算出的坝体典型点位移几乎没有差别，且各点位移随超载系数的变化过程线比较平稳，没有出现明显的突变点，图7(a)和(b)分别为无缝整体模型和开裂模型的典型点位移与超载系数的关系。两者比较可反映出裂缝对该拱坝超载整体安全度影响甚微。对于该拱坝的整体安全度，则根据超载过程中坝体和坝基塑性应变的发展过程，采用塑性屈服区贯通准则进行判断。

超载过程中，无缝整体模型和开裂模塑性变形情况也基本相同，均为F4和F5两断层附近首先开始屈服，但随着超载系数的增大，两断层附近的塑性变形区没有急剧扩展的趋势，而坝体建基面的塑性变形开展较快，当Kp=6.0时，建基面出现塑性屈服区贯通现象。从两断层的走向及与坝体的相对位置分析可知：F4和F5断层对坝体抗滑稳定性影响较小，因此该坝主要根据建基面的屈服情况来评价整体安全度。

图8(a)和(b)分别为无缝整体模型和开裂模型的建基面屈服情况，从图8可以看出：2种计算模型下，建基面屈服情况一致，均为当Kp=5.0时，塑性区开展面积较大，Kp=6.0时建基面出现塑性屈服区贯通现象，因此按塑性区贯通准则可判断该拱坝-地基系统整体安全度为6.0左右，且裂缝对整体安全度无显著影响。

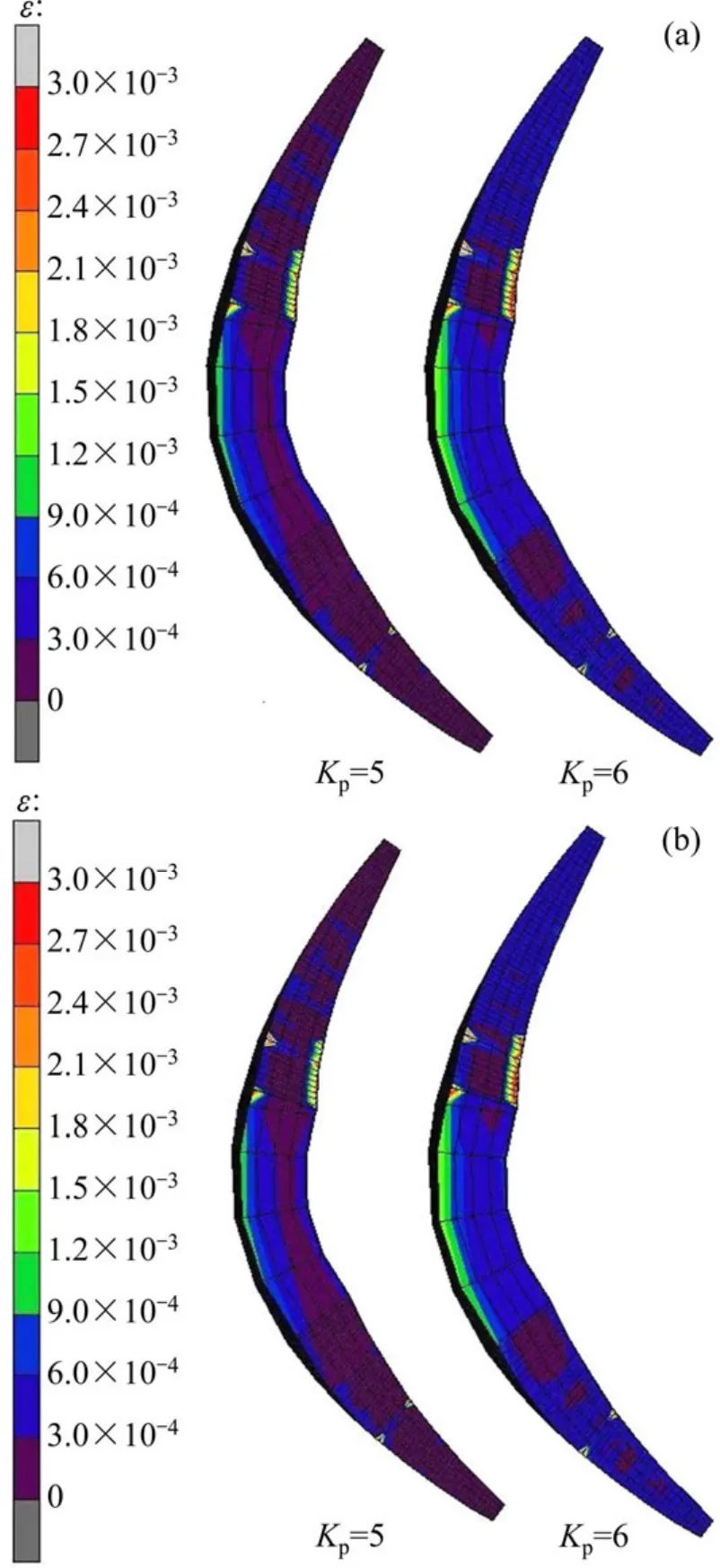
图8 建基面塑性区分布Fig.8 Sketch of plastic zone distribution on dam foundation

3.2.2 坝体弹塑性模型分析结果

坝体和坝基均采用基于 Drucker-Prage屈服准则的弹塑性本构模型。在超载系数由1.0按照0.5倍增量开始增大的过程中，当超载系数达到5.0时，无缝模型和开裂模型均出现迭代计算不收敛的情况。典型点位移随超载系数的变化规律如图9所示。

图9 坝体典型点顺河向位移与超载系数关系Fig.9 Relationship between displacement along river of typical points and overloading coefficient

超载过程中，2种计算模型的塑性变形发展情况基本相同，且裂缝不会加速坝体的屈服。坝体上游面塑性应变随超载系数的增大而增大，塑性区也逐渐增大，但是塑性区主要集中在坝体底部和坝体两侧靠近坝肩处；坝体下游面塑性区主要集中在坝体底部两侧以及拱冠梁顶部区域；Kp=2.0时，仅在建基面上游处出现塑性区坝体及建基面，Kp=4.0时，建基面两侧坝肩处塑性屈服区贯通，因此全部材料弹塑性分析时，该拱坝地基系统的整体安全度为4.0，同样裂缝对其整体安全度无显著影响。2种计算模型超载失稳时(Kp=4.0)坝体及建基面屈服情况如图10所示。

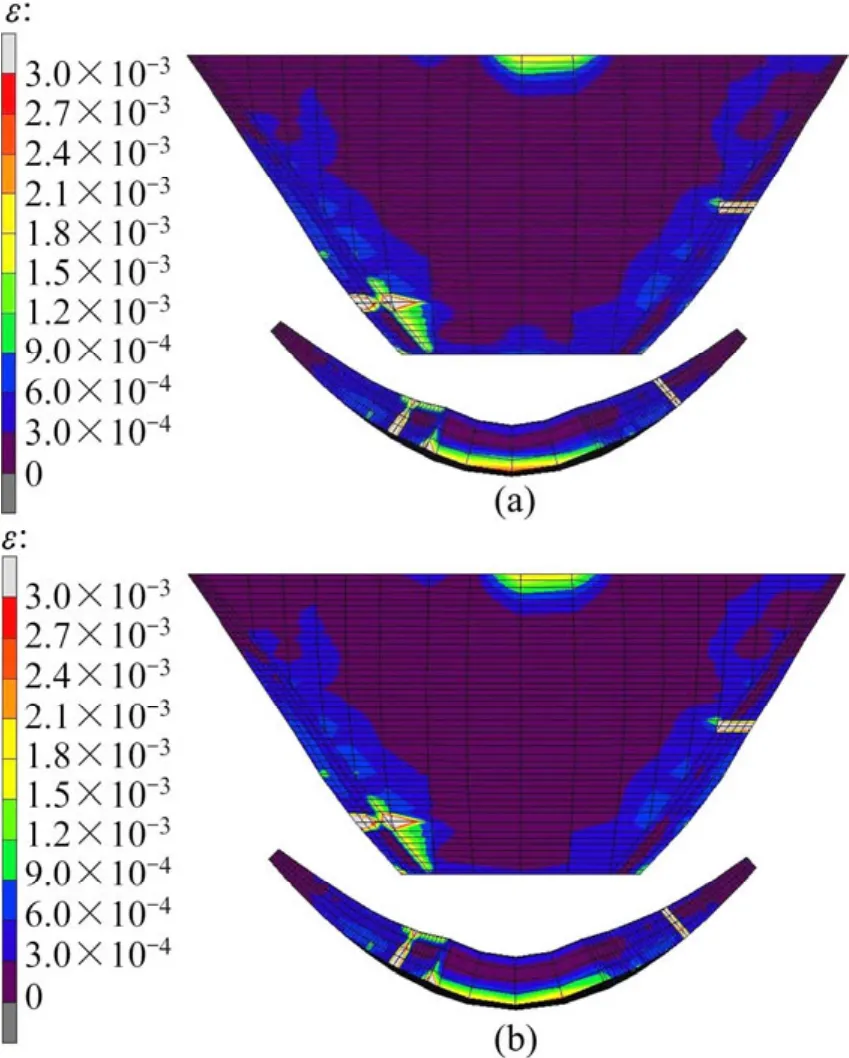
图10 坝体及建基面塑性区分布Fig.10 Sketch of plastic zone distribution on dam and foundation

综合收敛性、位移突变及塑性区贯通3种判据，分析结果表明此径向贯穿性裂缝对该拱坝−地基系统整体超载安全度无显著影响。坝体材料线弹性分析情况下拱坝−地基系统整体超载安全度为6.0，全部材料弹塑性分析情况下为4.0。

4 结语

(1) 仿真分析结果表明，该径向贯穿性裂缝对坝体应力位移分布规律影响较小，仅裂缝端部出现了应力集中现象，今后裂缝处理主要针对防渗工作以及防止裂缝进一步扩展而进行。

(2) 拱坝−地基系统超载整体安全度分析结果表明，裂缝对其整体安全度无显著影响，有无裂缝时系统各部位屈服发展规律基本一致，且裂缝不会加速坝体失稳，坝体材料线弹性分析时超载整体安全度为6.0左右，弹塑性时为4.0左右。参照国内其他拱坝计算结果，径向贯穿性裂缝影响下该拱坝整体安全度基本满足要求。

(3) 有限元分析时，材料本构模型的选择对整体安全度的评价影响较大。该碾压混凝土坝2种坝体材料本构模型计算结果表明，坝体材料线弹性计算所得整体安全度偏高，坝体材料弹塑性分析结果比较符合实际情况。

(4) 整体安全度评价目前多基于收敛性判据和突变性判据，然而2种判据评价结果相差较大，缺乏统一性，因此整体安全度评价准则的优化仍是今后需要解决的问题。

[1] 韦天琴, 刘海成, 宋加国.碾压混凝土坝开裂研究的进展[J].水力发电, 2005, 31(3): 37−38.WEI Tianqin, LIU Haicheng, SONG Jiaguo.Study advance on the cracking of RCC arch dams[J].Water Power, 2005, 31(3):37−38.

[2] 朱耀台, 詹树林.混凝土裂缝成因与防治措施研究[J].材料科学与工程学报, 2003, 21(5): 727−730.ZHU Yaotai, ZHAN Shulin.Study on reasons and prevention measures of cracking in concrete structure[J].Journal of Materials Science & Engineering, 2003, 21(5): 727−730.

[3] 刘耀儒, 王峻, 杨强, 等.小湾拱坝坝体裂缝对拱坝受力和稳定的影响研究[J].岩石力学与工程学报, 2010, 29(6):1132−1139.LIU Yaoru, WANG Jun, YANG Qiang, et al.Research on influences of cracking of Xiaowan arch dam on its stress and stability[J].Chinese Journal of Rock Mechanics and Engineering,2010, 29(6): 1132−1139.

[4] 傅少君, 陈胜宏, 邹丽春.小湾拱坝诱导底缝的三维有限元分析[J].水利学报, 2006, 37(1): 96−103.FU Shaojun, CHEN Shenhong, ZOU lichun.Analysis of bottom induced joint in arch dam of Xiaowan project by using 3-D FEM[J].journal of Hydtaulic Engineering, 2006, 37(1): 96−103.

[5] 夏雨.碾压混凝土高拱坝安全度评价研究[D].南宁: 广西大学土木建筑工程学院, 2010: 4−5.XIA Yu.Study of safety analysis on RCC dam[D].Nanning:Gang Xi University.School of Civil Engineering, 2010: 4−5.

[6] 张波, 徐兰玉.拱坝安全性研究[J].中国农村水利水电,2006(10): 107−109.ZHANG Bo, XU Lanyu.Safety analysis of arch dams[J].China Rural Water and Hydropower, 2006(10): 107−109.

[7] 任青文, 强向东, 赵引, 等.高拱坝沿建基面抗滑稳定性的分析方法研究[J].水利学报, 2002(2): 1−7.REN Qingwen, QIAN Xiangdong, ZHAO Yin, et al.Method for analyzing sliding resistance stability along the base surface of high arch dam[J].Journal of Hydtaulic Engineering, 2002(2):1−7.

[8] 徐福卫, 陈海玉.高拱坝沿建基面的上滑稳定性分析[J].水力发电, 2008, 34(3): 44−46.XU Fuwei, CHAN Haiyu.Study of stability against sliding along contact face between foundation and arch dam[J].Water Power,2008, 34(3): 44−46.

[9] 段庆伟, 耿克勤, 吴永平, 等.小湾拱坝变形承载力及整体安全度评价与分析[J].岩土力学, 2008, 29(增刊): 15−20.DUAN Qingwei, GENG Keqin, WU Yongping, et al.Evaluation of global safety degree of Xiaowan arch dam[J].Rock and Soil Mechanics, 2008, 29(Suppl): 15−20.

[10] 常晓林, 杨海云, 周伟, 等.重力坝沿建基面失稳破坏的真实安全度研究[J].岩土力学, 2008, 29(9): 2365−2372.CHANG Xiaolin, YANG Haiyun, ZHOU Wei, et al.Study of true degree of failure along foundation surface of gravity dam[J].Rock and Soil Mechanics, 2008, 29(9): 2365−2372.

[11] 余天堂, 任青文.锦屏高拱坝整体安全度评估[J].岩石力学与工程学报, 2007, 26(4): 787−794.YU Tiantang, REN Qingwen.Evaluation of global degree of Jingping high arch dam[J].Chinese Journal of Rock Mechanics and Engineering, 2007, 26(4): 787−794.

[12] 宁宇, 徐卫亚, 郑文棠, 等.白鹤滩水电站拱坝及坝肩加固效果分析及整体安全度评价[J].岩石力学与工程学报, 2008,27(9): 1890−1898.NING Yu, XU Weiya, ZHENG Wentang, et al.Reinforcement effect analysis and global safety evaluation of arch dam and abutment of Baihetan hydropower station[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(9): 1890−1898.

[13] 陈在铁, 任青文.高拱坝安全度评价研究[J].南京理工大学学报, 2005, 29(5): 623−626.CHEN Zaitie, REN Qingwen.High arch dam safety evaluation[J].Journal of Nanjing University of Science and Technology, 2005, 29(5): 623−626.

[14] 张仲卿.碾压混凝土拱坝[M].北京: 中国水利水电出版社,2001: 126−129.ZHANG Zhongqin.RCC arch dams[M].Beijing: China Water Power Press, 2001: 126−129.

[15] 娄一青, 顾冲时, 李君.基于突变理论的有限元强度折减法边坡失稳判据探讨[J].西安建筑科技大学学报: 自然科学版,2008, 40(3): 361−367.LOU Yiqing, GU Chongshi, LI Jun.Study on the slope failure criterion in the strength reduction finite element method based on catastrophe theory[J].Journal of Xi’an University of Architecture & Technology: Natural Science Edition, 2008,40(3): 361−367.