融合PPI和基因表达数据的关键蛋白质识别方法

(中南大学 信息科学与工程学院，湖南 长沙，410083)

关键蛋白质是细胞生命活动中所必需的蛋白质，利用基因剔除式突变将其移除会造成有关蛋白质复合体功能丧失，甚至导致生物体无法生存[1]，因此，识别关键蛋白质对于研究细胞的生长调控过程具有重要意义。同时，研究表明：致病基因往往表现为关键蛋白质[2]，关键蛋白质的识别对于病原生物学的研究以及药物设计也具有重要的意义。在生物学领域，一般利用基因敲除、RNA干扰等实验方法，通过观察生物体生存情况来辨别蛋白质的关键性。依靠生物实验识别关键蛋白质的方法虽然准确有效，但是代价高且效率低。近年来，随着酵母双杂交、串联亲和纯化、质谱分析等高通量的蛋白质组技术的发展[3]，可获得的蛋白质相互作用数据越来越多，使得在网络水平上预测关键蛋白质成为可能。已有研究表明，蛋白质的关键性与它在生物网络中所对应节点的拓扑特性密切相关[4]，因此，出现了一系列利用节点的中心性测度参数识别关键蛋白质的方法。最常用的一个中心性测度是度中心性(degree centrality)[5]，网络中某个给定节点的度中心性表示为与其直接相连的邻居节点的个数。Jeong等[5]提出“中心性−致死性”法则(centralitylethality rule)，该法则显示一个蛋白质参与的相互作用越多，这个蛋白质对细胞的生存也就越重要。除了最常用的度中心性以外，还有介数中心性[6]、接近度中心性[7]、子图中心性[8]、特征向量中心性[9]、信息中心性[10]、局部平均联通性[11]和边聚集系数之和[12]。其中：节点的介数中心性(betweenness centrality, BC)表示网络中所有最短路径中经过该节点的数目占所有最短路径数的比例；节点的接近度中心性(closeness centrality,CC)为反比于该节点到网络中其他所有节点的最短路径之和；节点的子图中心性(subgraph centrality, SC)是该节点参与网络闭合回路的总数；节点的特征向量中心性(eigenvector centrality, EC)被定义为网络邻接矩阵的主特征向量该节点的分量；节点的信息中心性(information centrality, IC)是测量以该节点为端点的路径的调和平均长度；节点的局部平均联通性(local average connectivity，LAC)是指该节点的邻居节点彼此之间公共邻居节点的个数之和除以该节点的邻居节点的个数；节点的边聚集系数之和(sum of edge clustering coefficient，SoECC)是指该节点所有连接边的聚集系数之和。这8种中心性测度都已被用于生物网络中关键蛋白质的预测，且被证实比较有效。然而，中心性测度如果仅仅依靠PPI数据识别关键蛋白质，预测的准确度比较依赖网络本身的可靠性。因此，本文作者提出一种新的中心性测度参数PeC，在PPI网络的基础上融合基因共表达数据信息，降低预测方法对蛋白质相互作用网络本身可靠性的依赖程度，并将提出的关键蛋白质预测方法PeC应用于酵母蛋白质相互作用网络。

1 融合基因表达的中心性测度PeC

考虑到高度的节点倾向于成为关键蛋白质，而关键蛋白质节点往往又成簇出现，并且具有较高的共表达特性[13]，所以，提出一种融合基因表达信息的新的中心性测度PeC。PPI网络可以表示成为1个无向图G(V,E)，每个节点表示1个蛋白质，每条边表示1种相互作用，其中V表示节点的集合，E表示边的集合。基因表达数据是生物学家通过生物实验得到，它表达了蛋白质生命运动的过程，在不同的时刻蛋白质X的基因表达值不同，可以表示为X(g1,g2, …,gk)，其中，gk表示蛋白质节点X在时刻k的基因表达值。为了清楚地描述中心性测度PeC，本文首先给出相关定义。

1.1 边聚集系数(ECC)

聚集系数最早由Watts和Strogatz提出，用于刻画网络中某个节点与其邻居之间的亲疏程度，是复杂网络中最重要的拓扑特征之一，已被广泛应用于蛋白质相互作用网络等较复杂网络的拓扑分析[14]。近年来，聚集系数的定义已由节点扩展到边，本文选用文献[15]中给出的边聚集系数(edge clustering coefficient,ECC)的定义。给定 PPI网络中的 1条边E(X,Y)，用N(X)和N(Y)分别表示节点X和节点Y的邻居节点的集合，则边E(X,Y)的边聚集系数被定义为

边聚集系数ECC(X,Y)是一个局部变量，刻画了边E(X,Y)的2个节点X和Y的亲疏程度。E(X,Y)的取值范围为[0,1]，其取值越大，表明节点X和节点Y属于同一个簇的可能性越大。

1.2 基因表达的皮尔逊相关系数(PCC)

基因表达数据是用来表示蛋白质生命运动的过程的一组数据，将其进行建模，并引入皮尔逊相关系数(pearson correlation coefficient, PCC)来度量相互作用蛋白质的基因共表达强弱程度，蛋白质X和Y的PCC定义为

其中：k为样本数，表示基因表达数据中的时刻数；Exp(X,i)和Exp(Y,i)分别为蛋白质X和Y的在i时刻的表达值；Exp(X)和Exp(Y)为蛋白质X和Y在所有时刻下的平均表达值；σ(X)和σ(Y)表示蛋白质X和Y在所有时刻表达值的标准方差。PCC(X,Y)的取值范围为[−1,1]，PCC(X,Y)＜0说明基因X和Y表现出负相关，PCC(X,Y)＞0说明基因X和Y表现出正相关，PCC(X,Y)=0说明基因X和Y不存在相关性。

1.3 中心性测度PeC

虽然“中心性−致死性”法则显示 1个蛋白质参与的相互作用越多，这个蛋白质越倾向于成为关键蛋白质，但研究表明，仍然存在一部分蛋白质具有较高的度，但不是关键蛋白质。通过实验发现，这类蛋白质参与的相互作用往往具有较低的边聚集系数，且基因共表达程度较低。例如，如图1所示非关键蛋白质YGR254W有67个邻居节点，但是它与邻居节点的边聚集系数的平均值仅为0.054，与邻居节点的共表达的皮尔逊系数PCC的平均值仅为0.003。

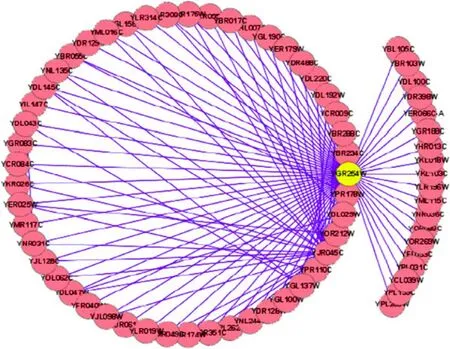
图1 非关键蛋白质YGR254W与邻居节点的关系图Fig.1 Relationship figure for non-essential protein YGR254W and its neighbors

基于对高度的非关键蛋白质的分析，以及关键蛋白质节点往往成簇出现且倾向于共表达的事实，利用边聚集系数(ECC)和皮尔逊相关系数(PCC)计算出边E(X,Y)属于同一簇的概率PC(X,Y)，定义如下：

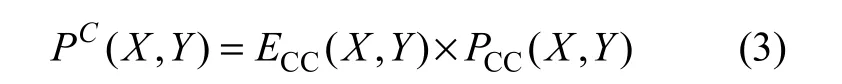
PC(X,Y)不但考虑了边E(X,Y)的节点X和Y在网络的拓扑特性的聚集程度，而且增加了节点X和Y基因共表达程度对于关键性的影响。考虑到高度的节点倾向于成为关键蛋白质，将PC(X,Y)看作边E(X,Y)的权值，则节点X的中心性测度PeC(X)即是X的连接边得权值之和：

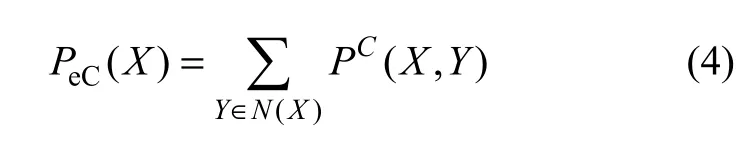
PeC综合考虑了边聚集系数和基因表达数据，构造边E(X,Y)加权度，可以将一部分度中心性较高但并不是关键蛋白质的节点排除，因此，具有较高的准确度。

2 实验数据及评估方法

2.1 实验数据

在所有物种中，酵母的蛋白质相互作用数据最为完备。因此，选择酵母蛋白质相互作用网络作为研究对象。实验所用的数据集来源于 MIPS[16]数据集，包含4 546个节点和12 319条相互作用。关键蛋白质数据是通过整合 MIPS[16]，SGD[17]，DEG[18]，SGDP[19]4个数据库中的数据得来，包含1 285个关键蛋白质。实验所用的基因表达数据来自于文献[20]，其中包含了6 777个基因在36个样本时刻下的基因表达值，有4 858个基因与酵母蛋白质相互作用网络相关联。通过比对整合的关键蛋白质集合，MIPS数据集包含1 016个关键蛋白质，3 195个非关键蛋白质和335个关键性未知的蛋白质。

2.2 评估方法

根据“排序−筛选”原则对PeC和8种中心性测度的预测结果进行比较。具体做法是：对于PeC和8种中心性测度参数按照从大到小的顺序排序，选出序列中前1%，5%，10%，15%，20%和25%的蛋白质作为候选关键蛋白质，通过与已知关键蛋白质数据集匹配，得到每种测度识别正确的关键蛋白质的数量并相互比较。除此之外，还引入敏感度(SN)，特异性(SP)，F-测度(F-measure)，正确率(ACC)这几个医学检验中的指标对PeC进行评估并与其他8种中心性测度结果比较。这几个评价指标的定义如下：

敏感度SN为关键蛋白质被正确地预测的比例。

特异性SP为非关键蛋白质被正确地排除的比例。

式中：PT表示测度参数识别的关键蛋白质与已知关键蛋白质匹配的数量；PF表示被算法误识别为关键蛋白质的非关键蛋白质的数量；NT表示非关键蛋白质被识别为非关键蛋白质的个数；NF表示测度参数没有识别出的关键蛋白质的数量。

F-测度Fmeasure为敏感度和特异性的调和平均值。

正确率ACC为

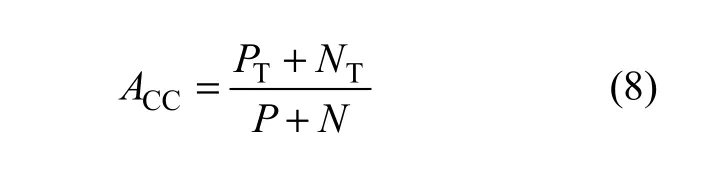
阳性预测值(PPV)VPP为选出的蛋白质中被正确地预测为关键蛋白质的比例。

阴性预测值(NPV)VNP为排除的蛋白质中被正确预测为非关键蛋白质的比例。

3 实验结果分析

每种测度参数识别正确的关键蛋白质数如图 2所示。

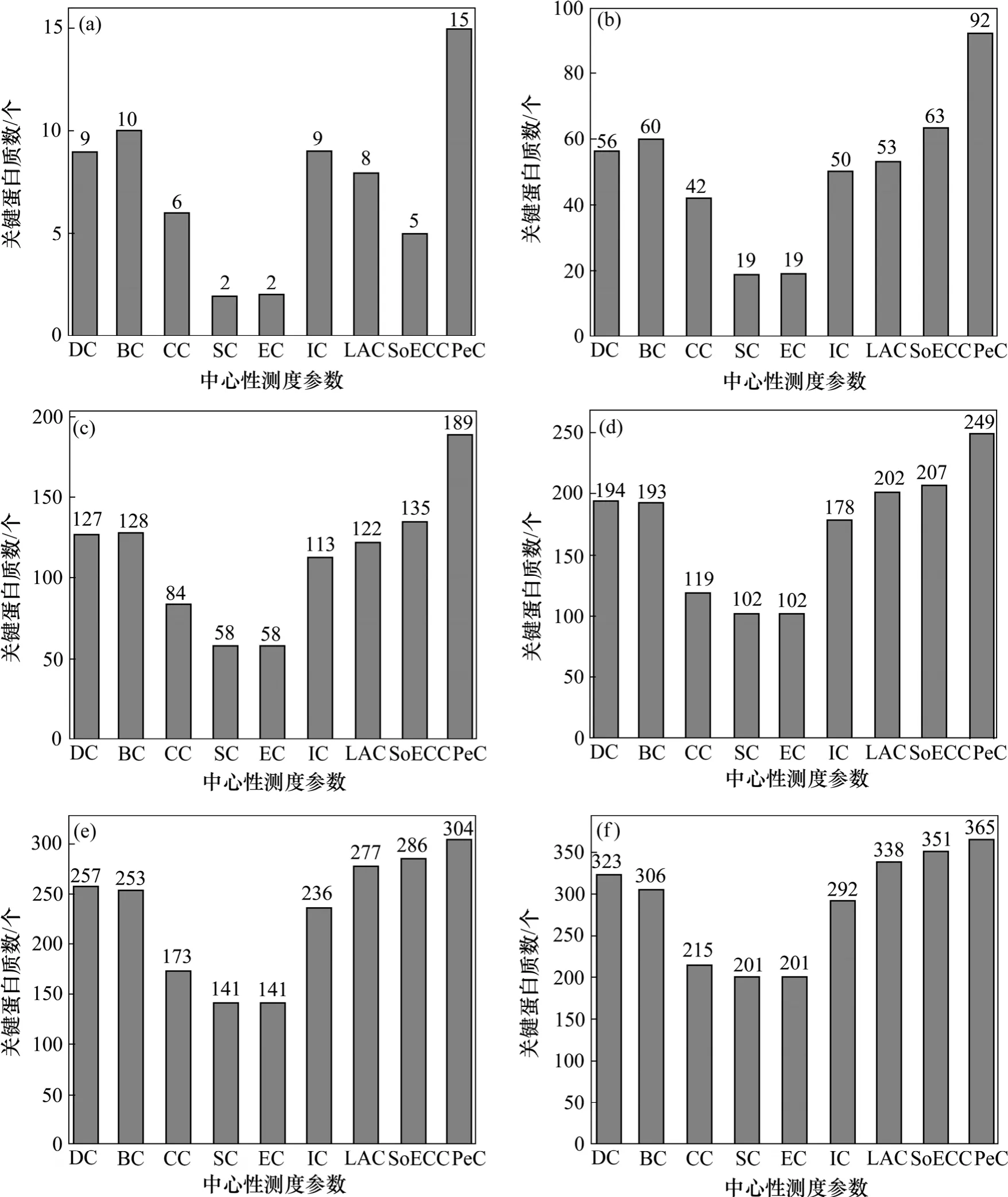
图2 根据PeC和其他8种中心性测度预测正确的关键蛋白质数Fig.2 Number of essential proteins by Pec and eight other centrality measures

从图2可以看出：根据PeC预测正确的关键蛋白质数量普遍高于8种中心性测度预测正确的关键蛋白质数。在任一样本水平，PeC比CC，SC和EC这3个测度参数的预测命中率高13%以上；在前1%，5%，10%样本水平，PeC比CC，SC和EC这3个测度参数的预测命中率高20%以上。

同时，为了更细致地比较PeC和其他8种中心性测度在预测不同数量的关键蛋白质时的准确性，比较了它们的Jackknife，实验结果如图3所示。从图3可以看出：PeC中心性测度在任一累积数量的蛋白质中识别的关键蛋白质都比其他8种中心性测度识别的多。

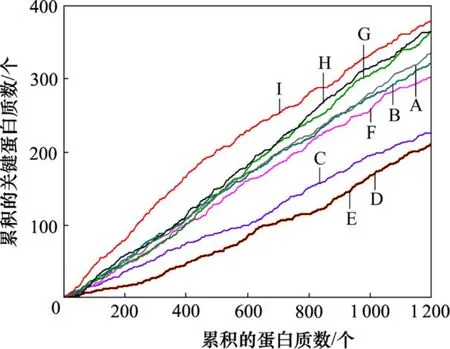
图3 PeC和其他8种中心性测度的JackknifeFig.3 Jackknife of PeC and eight other centrality measures

另外，引入敏感度(SN)、特异性(SP)、F测度(F-measure)、正确率(ACC)、阳性预测值(PPV)和阴性预测值(NPV)这几个评估指标对PeC和其他8种中心性测度结果进行评估比较，实验结果如表1所示。从表1可以看出：在任一指标(SN，SP，F-measure，ACC，PPV，NPV)下，PeC都具有最好的结果。

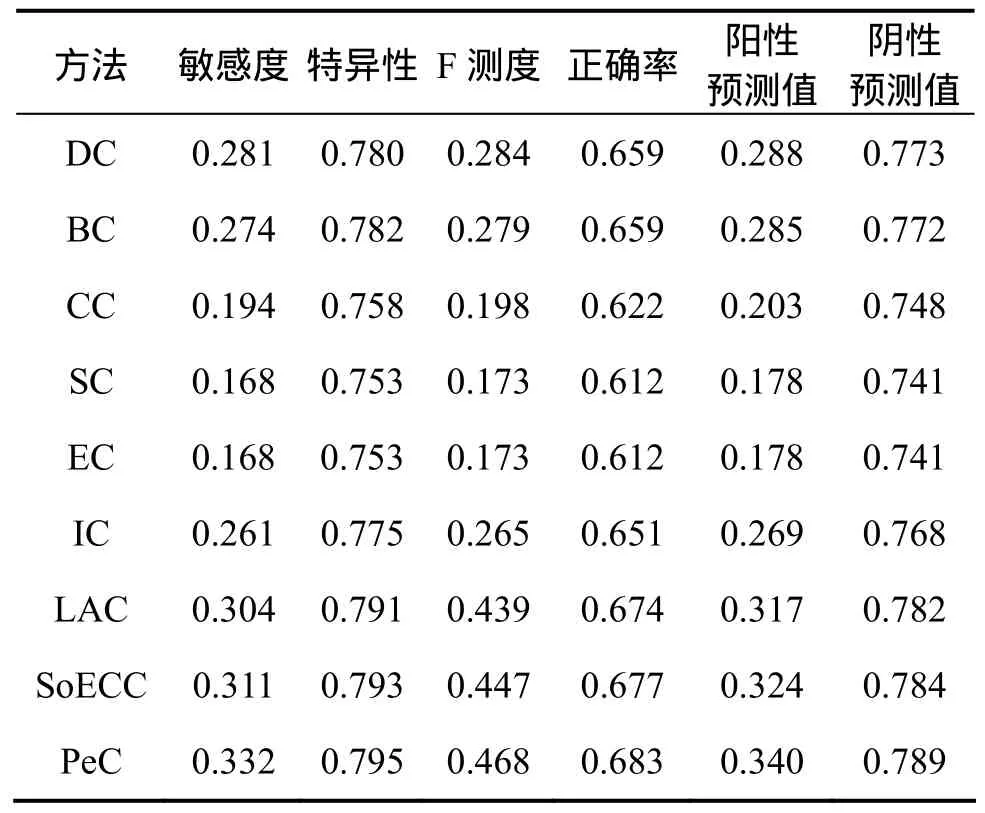
表1 PeC和其他8种中心性测度的各个评价指标的比较Table 1 Comparison of Evaluation Indicator by PeC and other eight centrality measures

4 结论

(1) 提出了一种新的融合了 PPI和基因表达数据的中心性测度(PeC)。

(2) 该中心性测度PeC在蛋白质相互作用网络拓扑特性的基础上融合了基因表达数据，降低了对蛋白质相互作用网络本身可靠性的依赖，提高了预测的准确性。与8种节点中心性测度参数对比，PeC能够预测出更多的关键蛋白质，且预测准确度更高。其中，在 MIPS数据集前 1%，5%，10%的样本水平，PeC比CC，SC和EC的预测准确度均提高了20%以上。

[1] Winzeler E A, Shoemaker D D, Astromoff A, et al.Functional characterization of the S.cerevisiae genome by gene deletion and parallel analysis[J].Science, 1999, 285: 901−906.

[2] Jeong H, Oltvai Z, Barabási A L.Prediction of protein essentiality based on genomic data [J].ComPlexUs, 2003, 1(1):19−28.

[3] Mering C, Krause R, Sne B, et al.Comparative assessment of large-scale data sets of protein–protein interactions[J].Nature,2002, 417: 399−403.

[4] Barabási AL., Oltvai ZN.Network biology: Understanding the cell’s functional organization[J].Nat Rev Genet, 2004, 5(2):101−113.

[5] Jeong H, Mason S, Barabási A L, et al.Lethality and centrality in protein networks[J].Nature, 2001, 411: 41−42.

[6] Joy M P, Brock A, Ingber D E, et al.High-betweenness proteins in the yeast protein interaction network[J].Journal of Biomedicine and Biotechnology, 2005(2): 96−103.

[7] Wuchty S, Stadler P F.Centers of complex networks[J].Journal of Theoretical Biology, 2003, 223(1): 45−53.

[8] Estrada E, Rodríguez-Velázquez J A.Subgraph centrality in complex networks[J].Phys Rev E, 2005, 71(5): 056103.

[9] Bonacich P F.Power and centrality: A family of measures[J].American Journal of Sociology, 1987, 92(5): 1170−1182.

[10] Stevenson K, Zelen M.Rethinking centrality: Methods and examples[J].Social Networks, 1989, 11(1): 1−37.

[11] LI Min, WANG Jianxin, CHEN Xiang, et al.A local average connectivity-based method for identifying essential proteins from the network level[J].Computational Biology and Chemistry,2011, 35: 143−150.

[12] WANG Huan, Li Min, Wang Jinxin, et al.New method for identifying essential proteins based on edge clustering coefficient[C]//7th International Symposium on Bioinformatics Research and Applications.Heidelberg: Springer-Verlag, 2011,6674: 87−98.

[13] PANG Kaifang, SHENG Huanye, MA Xiaotu.Understanding gene essentiality by finely characterizing hubs in the yeast protein interaction network[J].Biochemical and Biophysical Research Communications.2010, 401(1): 112−116.

[14] 李敏.蛋白质相互作用网络中复合物和功能模块挖掘算法研究[D].长沙: 中南大学信息科学与工程学院, 2008: 72−73.LI Min.Identifying protein complexes and functional modules in protein interaction networks[D].Changsha: Central South University.School of Information Science and Engineering,2008: 72−73.

[15] Watts D J, Strogatz S H.Collective dynamics of “small-world”networks[J].Nature, 1998, 393: 440−442

[16] Mewes H W, Frishman D, Mayer K F, et al.MIPS: analysis and annotation of proteins from whole genomes in 2005[J].Nucleic Acid Research, 2006, 34(1): 169−172.

[17] Cherry J M, Adler C, Ball C, et al.SGD: Saccharomyces genome database[J].Nucleic Acid Research, 1998, 26(1): 73−79.

[18] ZHANG Ren, LIN Yan.DEG 5.0: A database of essential genes in both prokaryotes and eukaryotes[J].Nucleic Acid Research,2009, 37(1): 455−458.

[19] Bruno A, Jef B, Carla C, et al.SGDP: Saccharomyces Genome Deletion Project [EB/OL].[2007−12−30] http://www-sequence.stanford.edu/group/yeast_deletion_project/deletions3.html.

[20] Tu B P, Kudlicki A, Rowicka M, et al.Logicof the yeast metabolic cycle: Temporal compartmentalization of cellular processes[J].Science, 2005, 310: 1152−1158.