基于遗传算法优化带有密闭气罩造纸机干燥部送风温度

汤 伟 周 阳 苏亚洲

(陕西科技大学电气与信息工程学院，陕西西安，710021)

在纸张的抄造过程中，纸张进入干燥部后，烘缸内通入蒸汽的热量通过烘缸表面传递给纸张，纸张中水分由于吸收热量而蒸发成水蒸气。对于带有密闭气罩的造纸机干燥部，此时通入密闭气罩的热风与水蒸气结合，形成湿热空气，通过密闭气罩顶部排风机排出气罩外［1］;而通入密闭气罩的热风是由空气经热回收系统回收的蒸汽冷凝水、二次蒸汽以及新鲜蒸汽加热所得，因此送风温度对干燥部的蒸汽消耗量有一定的影响。虽然干燥部的脱水量仅为纸张抄造全过程脱水总量的1%～2%，但干部脱水费用却为湿部脱水费用的9～70倍，干燥部消耗的蒸汽量占制浆造纸生产过程蒸汽消耗总量的65%以上［2-3］，所以对送风温度的优化是降低干燥部蒸汽消耗量的一个有效手段。

随着造纸机幅宽的增加、车速的提高，生产过程蒸汽用量的加大使各造纸企业在经济效益上有一定的损失。因此，各造纸企业除了对造纸机干燥部硬件基础设施上进行有效的改造外，优化送风温度对降低造纸机干燥部蒸汽消耗量具有重要的意义。本文在分析干燥部送风温度对蒸汽消耗量影响的基础上，提出了利用遗传算法对干燥部送风温度优化的一种方法，并对该方法进行了仿真验证。

1 送风温度对蒸汽消耗量的影响分析

在分析送风温度对蒸汽消耗量影响前，首先要根据干燥部能量守恒定律得出关系式(1)，即进干燥部热量等于出干燥部热量。纸机干燥部热能示意图如图1所示，其中:I4为送入热风带入的热量，I5为渗入风带入的热量，Q1为蒸汽通过烘缸向纸张提供的热量，I2为湿纸幅进入干燥部时带入的热量，Qr为热损失，I6为气罩排风带出的热量，I3为纸幅出干燥部带出的热量［4］。

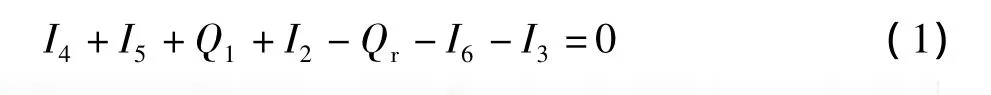
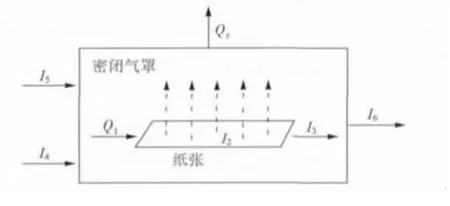
图1 纸机干燥部热能示意图

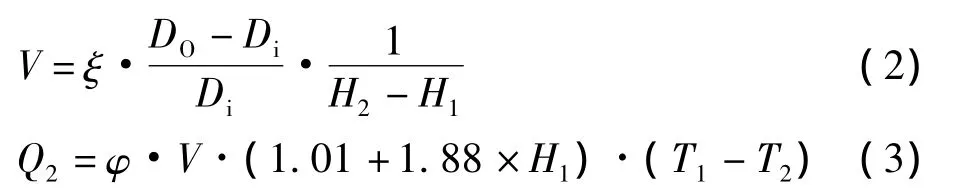
在式 (2)中，Di为进纸干度，DO为出纸干度，ξ为系数，取值为1000;式 (3)中，φ为气罩平衡系数，一般为0.75～0.85;H1为进风湿度，H2为排风湿度，T1为进风温度，T2排风露点温度。通入烘缸蒸汽释放的热量Q1可通过式 (1)、式 (3)求出。

在造纸机其他参数稳定的前提下，由式 (3)可知，蒸汽提供给加热器所释放的热量越低，送风温度越低，但是过低的干燥部送风温度会引起过低的袋区混合空气温度，容易导致蒸发效率降低。因为纸幅中水分从纸幅内部转移到纸幅表面时容易形成冷凝水，袋区混合气体温度过低会导致袋区相对湿度上升，湿空气中的水分较容易冷凝，冷凝水容易导致纸病的形成，因此干燥部送风温度不宜过低。然而，造纸机干燥部送风温度上升，烘缸供热可下降，但总的蒸汽消耗量将上升。原因是用于加热的送风蒸汽温度在130℃左右或更高，其蒸汽冷凝水温度略高于送风温度 (95～110℃，常用送风温度值设计范围)，若烘缸通入的新鲜蒸汽与用于送风加热的蒸汽量相同，但是其冷凝水温度可降至90℃［5］，所以，干燥部送风温度不宜过高。目前，各造纸企业送风温度值都是根

在抄纸过程中，对于吨纸而言，纸机干燥部通入送风量取决于湿纸幅水蒸气蒸发量、气罩性能、送风温湿度和排风温湿度等参数。吨纸蒸汽消耗量由两部分组成，一部分用于通过烘缸给纸张提供热量，另一部分用于加热器来加热送入的冷风。生产吨纸所消耗的干空气量V可由式 (2)求出，进而可以求出蒸汽提供给加热器的热量Q2，计算公式如式 (3)所示。据人工经验设置在95℃左右，缺乏科学性，同时是否对蒸汽消耗量造成了一定的浪费，也无法得知。根据表1中造纸机的参数［1］，造纸机干燥部送风温度选择在95～110℃变化时，得到送风温度对加热送风蒸汽消耗量的影响 (见图2)。从图2可看出，随着送风温度的上升，加热送风蒸汽消耗量也随之上升。根据上述分析，蒸汽消耗量为用于加热送风蒸汽量与通入烘缸蒸汽量之和，所以必然存在一个最优的送风温度值使得吨纸蒸汽消耗量最少。

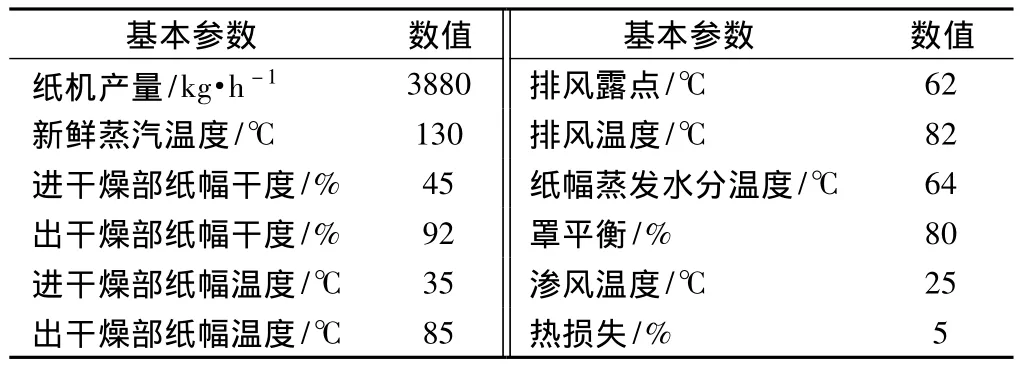
表1 带有密闭气罩造纸机基本参数

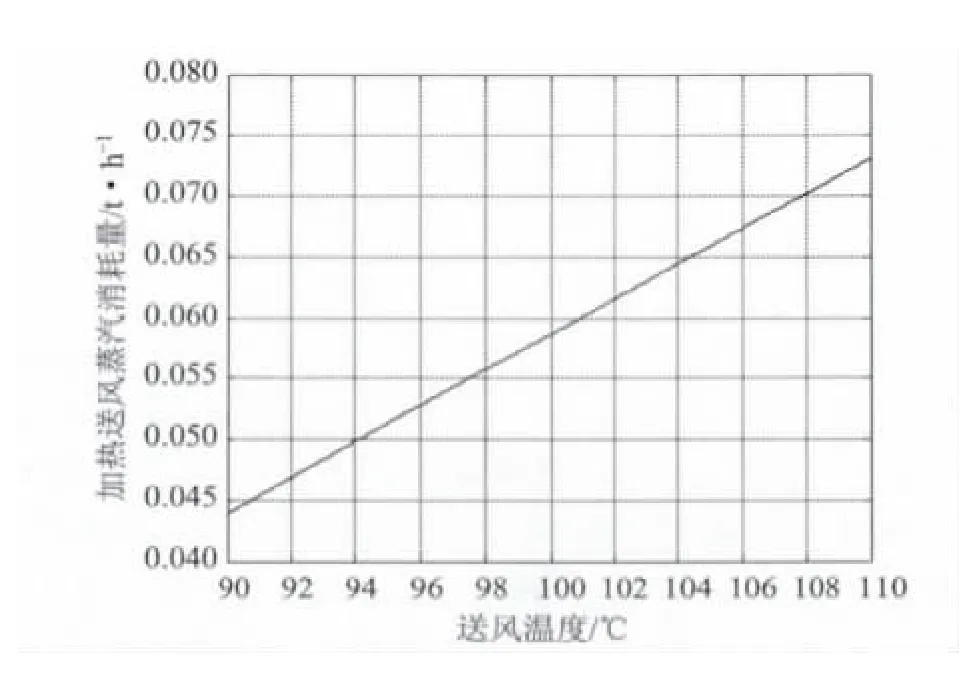
图2 加热送风蒸汽消耗量仿真图

2 遗传算法优化送风温度

求解优化问题有单纯形法、梯度法、牛顿法等多种方法，这些方法虽然都具有良好的寻优特性，但其缺陷却不容忽视。单纯形法和梯度法对初始值有一定的要求，容易导致局部寻优;牛顿法则要求计算目标函数Hesse矩阵，计算量大。遗传算法 (Genetic Algorithms)是模拟自然界遗传机制和生物进化论而成的一种并行随机搜索最优方法。上述各方法相比，遗传算法能够最大程度地实现全局最优，而且很适合求解多变量、单目标的约束优化问题，计算量相对较小，是一种高效的优化方法，同时由于纸机干燥部模型较复杂，并对优化后输出温度值精度有一定要求，因此，本研究利用遗传算法对送风温度进行优化，利用遗传算法随机搜索最优的特点，对送风温度值进行预测，从而使得吨纸蒸汽消耗量减少，达到节能环保的目的。遗传算法主要包括以下几部分:创建种群、设置自适应度函数、通过选择、交叉、变异算子寻找最优送风温度。

(1)在利用遗传算法对送风温度优化时，由于送风温度范围较广 (90～120℃)，为了提高优化精度、缩短个体串长，即个体的每个基因值用某一范围内的浮点数来表示。优点是不必进行数制转换，可直接进行遗传操作。编码后所得到的分布范围即设定为初始群体。

(2)适应度函数也称为评价函数，是根据目标函数确定的用于区分群体中个体好坏的标准，适应度较高的个体遗传到下一代的概率就较大。为了满足优化温度的准确性、优化范围的全局性，若令个体适应度值为F(f(x))，则设置自适应函数如式 (4)所示，其中cmax为一个适当的相对比较大的数，是目标函数蒸汽消耗量f(x)的最大值估计，也可以是一个合适的输入值［6］。该适应度函数克服了利用目标函数直接转化成为适应度函数所产生的选择概率为负和不能体现种群平均性能的缺陷。

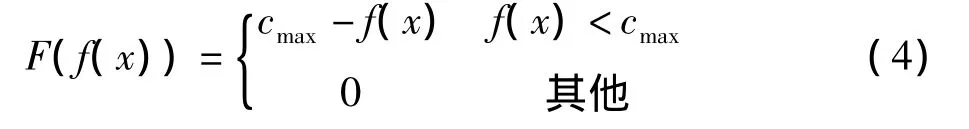
(3)通过选择、交叉、变异算法来选择出最优适应度值对应的送风温度。本研究采用的选择算子是比例选择方式，一种回放式的随机采样方法，利用各个个体适应度所占比例的大小决定其遗传的可能性，这种特征保证了优化温度过程是在全局范围内寻优，并且方法简单，计算量小。如令每个个体的选择概率为Pi，见式 (5)，式中Fi为个体i对应的适应度值，n为种群个体数。

由于个体编码采用的是实数编码，在遗传算法中针对实数编码的交叉算子一般选择实数交叉法产生新的个体，若第r个个体ar与第s个个体as在j位交叉，实数交叉法如式 (6)与式 (7)所示，式 (6)与式 (7)中，arj、asj为产生的新个体，c是 ［0，1］之间的随机数［7］。

变异是一种产生新个体的辅助方法，但其却决定了遗传算法的局部寻优能力，为了改善遗传算法的局部寻优能力，提高对送风温度优化值的准确性，变异算子要求能在某一重点区域内进行局部寻优。非均匀变异则是一种满足实数编码的理想变异算子。非均匀变异算子如式 (8)、式 (9)所示，令aij为第i个个体的第j个基因进行变异。式中，t为当前迭代次数，T为最大进化次数，amax、amin分别为基因aij的上下限，random(0，1)表示随机在0和1中取一个值，b是决定对迭代次数依赖程度的系统参数，本研究中b取值为2，r为 ［0，1］范围内符合均匀分布的随机数［8］。非均匀变异算子初始阶段在整个空间内搜索 (当t很小的时候)，随着t的逐渐增大，搜索主要集中于若干个局部范围精确搜索。

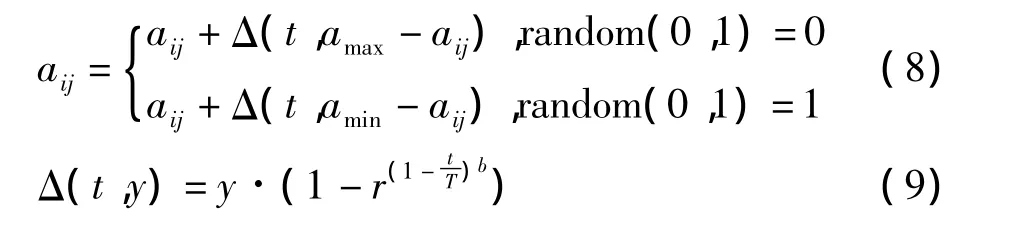
以造纸机干燥部送风温度为优化变量，根据能量守恒定律，将吨纸的蒸汽消耗量作为目标函数，利用遗传算法对送风温度进行优化，遗传算法优化送风温度流程如图3所示。从图3看出，将送风温度优化取值范围设为90～120℃，利用编码原理对其编码，产生n个种群，根据目标函数的特点，设置相应的适应度函数并计算出适应值，利用选择、交叉、变异遗传算子进行遗传运算，若运算后，得到的温度值满足精度要求，输出优化后温度值，程序结束。否则，返回至“设置适应度函数并计算适应值”步骤，循环运算，直到满足截止条件。

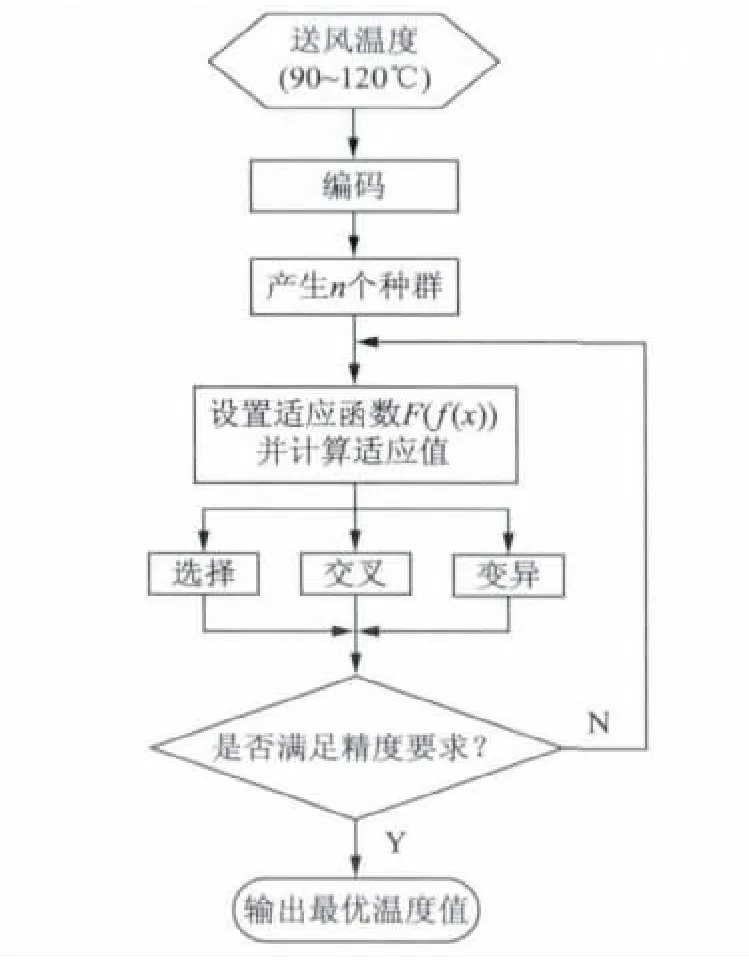
图3 遗传算法优化送风温度流程图

3 仿真与分析

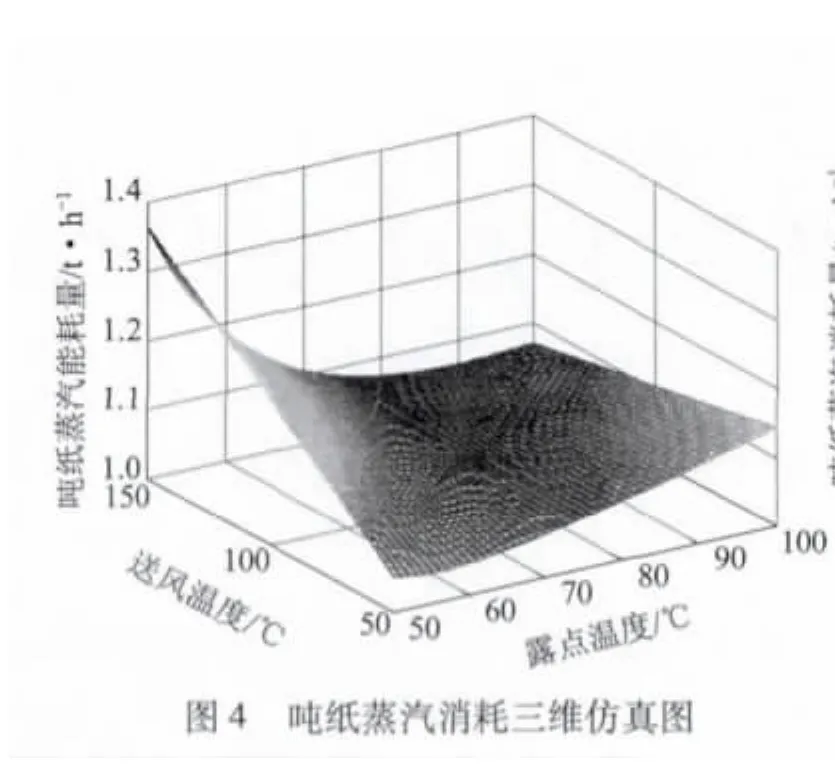
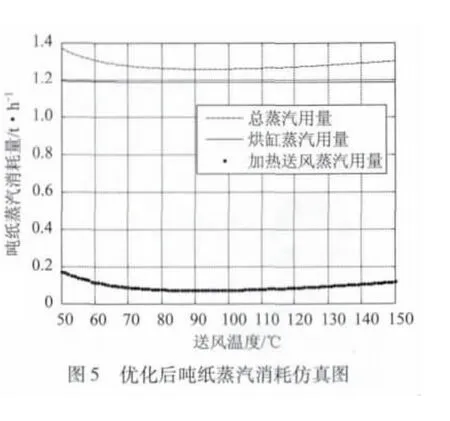
本仿真采用的带有密闭气罩造纸机基本参数如表1所示。以蒸汽消耗量、送风温度以及露点温度为坐标轴，仿真结果如图4所示，可知最少蒸汽消耗量的送风温度值存在。利用遗传算法对干燥部送风温度优化后，输出的最优温度值为96.61℃，吨纸蒸汽消耗量最少，为1.259 t。仿真结果如图5所示。从图5可以看出，随着送风温度的上升，吨纸的蒸汽能耗量出现先下降后上升的趋势，在送风温度在96℃左右变化时，吨纸蒸汽消耗量最少。吨纸蒸汽消耗量为通入烘缸消耗量W1与通入加热器的蒸汽消耗量W2之和，在实际生产中通常利用式 (10)计算。

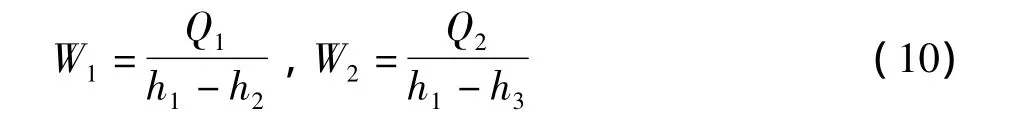
式中，Q1为蒸汽通过烘缸所提供热量，Q2为蒸汽通过加热器所提供热量，h1为蒸汽焓值，h2为烘缸排出冷凝水焓值，h3为加热器排出冷凝水焓值，可根据式 (1)、式 (3)知Q1、Q2，进而得到吨纸平均蒸汽消耗量约为1.55 t。经优化后吨纸蒸汽量可以节约0.27 t。对于造纸企业，若每天生产时间按照23 h计算，1年可节约5万t左右蒸汽 (0.291 t蒸汽/吨纸×20 t纸/h×23 h/d×360 d/a)，每吨蒸汽按照100元计算，1年可节约500万元，对于造纸企业是一种提高经济效益的有效手段。

4 结语

针对影响吨纸蒸汽消耗量的因素进风温度，以带有密闭气罩造纸机干燥部进风温度优化为例，进行切实有效分析。利用能量守恒定律对造纸机干燥部进风温度对干燥部蒸汽消耗量的影响做了分析，并利用遗传算法对送风温度进行优化。实验仿真结果表明，经优化后，吨纸蒸汽消耗量有一定的降低。对造纸机干燥部控制系统设计以及实际生产具有一定的参考价值。

［1］ Mardon J，Vyse R，Ely D．Paper machine efficiency:the most important parameter，how to get it and how to keep it［J］．Pulp ＆ Paper Canada，1992，92(12):285．

［2］ Zhou L C．The closed hood of paper machine and its design highlights［J］．China Pulp ＆ Paper Industry，2006，27(10):54．周乐才．纸机封闭式气罩及其设计要点［J］．中华纸业，2006，27(10):54．

［3］ Shixian paper mill．Knowledge of ventilation heat recovery system for high-speed paper machine-9#paper machine production practice of Shixian paper mill［C］//Nanjing，China Paper Association Ninth Annual Conference Proceedings，1999．石岘造纸厂．对高速纸机通风热回收系统的认识——石岘造纸厂9#纸机的生产实践［C］//中国造纸学会第九届学术年会论文集，南京，1999．

［4］ GONG Zhen-xiang，LIU Zhen-yi，LI Shen-xian，et al．Heat balance of drying section and its computer aided calculation［J］．China Pulp＆ Paper，1993，(3):31．宫振祥，刘振义，李生谦，等．纸机干燥部热平衡及其计算机辅助计算［J］．中国造纸，1993，3:31．

［5］ Yao X Y．Energy-saving control of hot air changing system in paper machine dryer section［D］．Nanjing，Nanjing Forestry University，2010．姚新跃．造纸机干燥部热风交换系统节能控制的研究［D］．南京:南京林业大学，2010．

［6］ Lei Y J，Zhang W S，Li X W，et al．MATLAB genetic algorithm toolbox and application［M］．Beijing，Xi'an University of Electronic Science and Technology Press，2005．雷英杰，张善文，李续武，等．MATLAB遗传算法工具箱及应用［M］．北京:西安电子科技大学出版社，2005．

［7］ Ren X H，Xu W D，Liu L X，et al．Thermal error compensation on cnc machine tools based on ga-bp neural network［J］．Manufacturing Automation，2011，33(5):41．任小洪，徐卫东，刘立新，等．基于遗传算法优化BP神经网络的数控机床热误差补偿［J］．制造业自动化，2011，33(5):41．

［8］ Zhao X C．Convergence analysis of evolutionary algorithm based on non-uniform mutation for multi-dimensional and multimodal functions［J］．Journal of Systems Science and Mathematical Sciences，2010，30(2):218．赵新超．基于非均匀变异的进化算法对高维多峰函数的收敛性分析［J］．统系科学与数学，2010，30(2):218．