无限长杆自由纵振动的傅氏解

屈军 徐华锋 崔执凤

(安徽师范大学物理系 安徽 芜湖 241000)

目前的数学物理方程教科书中指明[1,2]：对于无限长杆的自由纵振动，或者电阻、电漏等无限长传输线上电流、电压的变化，都可归结为以下的初值问题.

(1)

教科书采用的基本是达朗贝尔解法[1,2]，达朗贝尔解法先求出通解，然后从中挑出特解.虽然该方法不是数理方程常用的方法，但是思路容易理解，且物理概念清晰，解答过程简单明了.在实际的教学过程中，不失一般性，该类问题也可从傅氏积分的方法入手，灵活运用狄拉克函数的特性，得到相同形式的解.具体过程如下：

对u(x,t)进行分离变量，代到泛定方程中

(2)

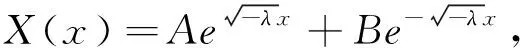
B(μ)sinμxcosaμt+C(μ)cosμxsinaμt+

D(μ)sinμxsinaμt]dμ

(3)

结合初值条件

u(x,0)=φ(x)=

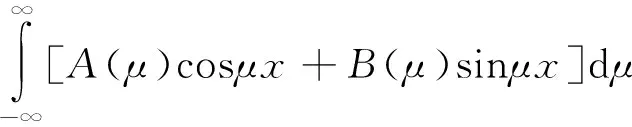
ut(x,0)=ψ(x)=

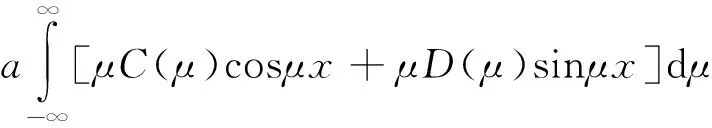
(4)

相应系数为

(5)

因此，方程的解可写为

(6)

积分一共四项，第一、二项和为

δ(ξ-x-at)]dξ=

(7)

第三、四项和为

sinμ(ξ-x-at)]dμ=

sinμ(ξ-x-at)]dμ

(8)

讨论

(1)当ξ>x+at，

ξ-x-at>x+at-x-at=0；

ξ-x+at>x+at-x+at=2at>0；

(2)当ξ

ξ-x+at

ξ-x-at

(2)当x-at<ξ

ξ-x+at>x-at-x+at=0→ξ-x+at>0，

ξ-x-at

(9)

利用公式[2]

(10)

从式(8)得到

sinμ(ξ-x-at)]dμ=

sinμ(ξ-x-at)]dμ+

sinμ(ξ-x-at)]dμ+

sinμ(ξ-x-at)]dμ=

(11)

故原初值问题解为

(12)

结果与达朗贝尔解法的结果完全一致[1,2].该方法简单明了，对更好地理解偏微分方程解的一般性有一定的帮助作用.

参考文献

1 梁昆淼.数学物理方法(第3版).北京:高等教育出版社,1998. 170

2 四川大学数学系.高等数学第四册(第3版).北京:高等教育出版社, 2009.121,230