钢管混凝土拱均匀温差设计取值研究

陈津凯， 陈宝春， 刘振宇， 余新盟

(1. 福州大学 土木工程学院， 福建 福州 350108； 2. 华侨大学 土木工程学院， 福建 厦门 361021)

钢管混凝土拱桥的主拱多为超静定结构，截面平均温度变化会在拱中产生附加内力，称为温度次内力。由于钢管混凝土拱肋是由钢和混凝土两种材料组成，且钢管与管内混凝土的施工又不是同步进行，所以，它与其他类型桥梁的温度作用有所不同。我国现行的《公路桥涵设计通用规范》[1](以下简称通规)没有对其温度计算做出明确规定，因此，国内学者已对这个问题开展了深入的研究。文献[2]提出“计算合龙温度”的概念，文献[3，4]以单圆管截面、文献[5，6]以哑铃形截面为研究对象开展了研究，文献[7]对一座钢管混凝土桁式拱桥进行实桥观测，分析了桁拱温度场的分布规律。在上述研究的基础上，以福建省为应用地区，福建省地方建设标准DBJ/T13-136-2011《钢管混凝土拱桥技术规程》[8](以下简称DBJ/T13-136-2011)提出了钢管混凝土拱均匀温度作用的设计取值方法。

2011年3月，《钢管混凝土拱桥技术规范》列入国家工程建设标准(以下简称国标)的制定任务。编制时，为了探讨如何将DBJ/T13-136-2011中钢管混凝土拱均匀温度作用设计取值方法推广应用至全国范围，需开展相应的研究。根据文献[9]分析可知，在环境温度和弦管管径相同的情况下，实肋拱和桁肋拱的计算合龙温度取值仅相差0.25℃；最高、最低有效温度取值相同。因此，在不失一般性的前提下，本文以一座钢管混凝土桁拱为研究对象，采用有限元软件ANSYS，应用从我国三个不同地区采集到的环境温度资料进行分析，讨论DBJ/T13-136-2011中计算合龙温度取值方法精度及温度次内力与有限元理论值(以下简称理论值)的差异；对钢管混凝土拱截面平均温度进行计算分析，以提出适合于全国钢管混凝土拱桥设计的有效温度取值方法。

1 DBJ/T13-136-2011均匀温差设计取值简介

1.1 计算合龙温度

研究表明[2]，钢管混凝土拱计算合龙温度是环境温度与管内混凝土水化热综合作用的结果，最主要的影响因素是管内混凝土浇筑后28 d内的平均气温和弦管管径。DBJ/T13-136-2011推荐的钢管混凝土拱桥计算合龙温度公式为：

(1)

式中：T28为钢管内混凝土浇注后28 d内的平均气温(℃)；D为钢管外径(m)；T0为考虑管内混凝土水化热作用的附加升温值，为3.0℃～5.0℃，冬季取小值，夏季取大值，混凝土强度等级低于C40时，在此基础上减1.0℃。

T28可视为当地的月平均气温，它是一个相对稳定的值。设计人员根据管内混凝土浇筑的日期，可以从当地历史气象资料得到月平均气温，代入式(1)计算。

1.2 有效温度

有效温度用于计算结构在均匀温度场作用下，结构相对于基准温度的温度变形与内力，分为最高有效温度和最低有效温度。钢管混凝土拱截面有效温度的最主要影响因素是环境温度和弦管管径。根据福建省各地的气候条件，将全省分为三个地区进行分析，根据分析结果，DBJ/T13-136-2011推荐有效温度按表1取用。

表1 福建省最高、最低有效温度标准值

注：钢管外径D<0.75 m时，最低有效温度取括号内的值。

2 研究方法

2.1 研究对象

以一座钢管混凝土桁拱为研究对象。该桥主跨跨径为150 m，矢跨比为1/5，拱轴线为空间悬链线。主拱肋为四肢钢管桁架式断面，拱肋高3.65 m，拱肋宽2.1 m。标准段拱肋上下弦管为Ф850 mm×14 mm(拱脚段为Ф850 mm×16 mm)的钢管，腹杆采用Ф350 mm×10 mm无缝钢管。拱肋上下弦管内填50号微膨胀混凝土(图1)。该桥的具体资料见文献[10]。

图1 拱肋横截面/mm

2.2 计算方法

本研究对钢管混凝土拱截面的温度场和温度次内力计算均采用有限元分析方法，应用ANSYS通用程序进行分析。钢管混凝土拱日照下的温度场是一个非线性的、瞬态的传热问题。假定全拱沿拱轴方向各截面温度场相同，可将三维温度场问题简化为平面问题进行分析。对于复杂的热交换边界条件是将太阳辐射、热辐射和对流三种热流，用对流来等效代替施加，将综合换热系数h、综合气温T赋给边界上的节点。对于钢管混凝土拱的温度次内力分析就是在温度荷载作用下的结构分析，ANSYS许多结构静力分析单元都具有温度荷载分析功能。

钢管混凝土拱截面有效温度的有限元计算就是求解截面在日照和环境温度共同作用下的温度场变化过程中的极值。采用PLANE55单元对截面进行划分，将每个单元的温度按面积作为权重求得截面每个时刻的平均温度，进而得到截面极值温度。

计算合龙温度的有限元计算方法是：先计算拱肋弦管截面温度场，采用增量法，以1 h为单位时段计算从混凝土浇筑完成至此后的28 d内，钢管混凝土拱在水化热和日照、环境温度共同作用下的温度场变化过程，然后求出每时刻截面的平均温度，进而得到每个时段内拱的平均温度增量ΔTi和28 d时的截面平均温度t28。将不同时刻(每小时)截面温度荷载ΔTi施加在拱的结构模型上，连续计算28 d并将每个时段内的温度内力累加，最终得到28 d后的温度内力。以此内力和t28，反算截面内力为0时的温度值，该值即为拱的计算合龙温度。

实际工程中，桁拱各弦管在不同时间完成管内混凝土浇注的，各弦管平均温度不同，但由于处于同一时期，因此不会相差太大。研究表明[11]，差值不会超过1.4℃，对于拱结构总内力的影响极小。因此，为简化计算，可以假设各弦管混凝土是同时灌注完成的，初始温度取浇筑时的环境温度。在施工阶段，拱肋表面涂层为红色漆，而成桥后涂层为银白色漆。由于确定钢管混凝土拱的计算合龙温度需要对施工过程的温度场进行分析，而有效温度主要考虑成桥后相当长服务时间内的影响，因此在计算该拱的计算合龙温度和有效温度时，钢管表面对太阳辐射的吸收系数α分别取为0.7和0.55[12,13]。

2.3 材料特性

由于混凝土刚度是逐渐形成的，28 d内大气温度周期性变化在混凝土内积累了应力；水化热使管内混凝土升温，随后慢慢降温，在混凝土内积累了应力。因此该过程中每个时段的计算应采用对应的结构刚度。混凝土水化热模型根据文献[14]采用复合指数式，弹性模量增长规律参考文献[15]，按式(2)确定：

E(t)=Ec(1-β×e-0.09t)

(2)

式中，Ec为混凝土最终弹性模量；E(t)为龄期为t的弹性模量；系数β=1。

对于本文算例，混凝土最终弹性模量为3.5×104MPa，代入式(2)可以确定该混凝土弹性模量增长曲线。

2.4 有限元模型

采用大型通用软件ANSYS进行建模分析。截面温度场计算采用PLANE55热单元进行单元划分，全截面共划分成340个单元。对于温度次内力的计算，将拱肋简化为杆系结构，采用BEAM188 梁单元模拟，共计471个节点，906个单元。模型经实桥在日照作用下实测温度场验证，见文献[7]。

2.5 分析参数

钢管混凝土拱的温度场与环境温度、太阳辐射、水化热、钢管管径、混凝土入仓温度和空钢管合龙温度等因素有关。研究表明[2]，在计算合龙温度中，影响最大的是环境温度与管内混凝土水化热；在有效温度中，最主要的影响因素是环境温度和弦管管径。为此，本文取各地的环境温度和弦管管径的大小为主要分析参数。

为了对比，本文分析时，桥梁对象相同，通过将其置于福建省漳州市(华东温热地区)、四川省雅安市(西南寒冷地区)和河南省南阳市(华中寒冷地区)三个不同区域实测环境温度下，通过有限元模型计算，来分析不同气温条件对计算合龙温度与有效温度的影响。对于超静定拱来说，当基准温度取值较高，有效温度取值较低时的温降对结构更为不利。因此，分析时，选取夏季实测温度计算合龙温度，式(1)中T0取5.0℃。

在我国已建的钢管混凝土拱桥中，弦管的管径D一般为550～1500 mm[16]。为了研究管径变化对均匀温差设计取值的影响，选择了D1=550 mm、D2=850 mm、D3=1200 mm和D4=1500 mm，共4种管径尺寸进行计算分析。需要指出的是，一般情况下，管径随着桥梁跨径的增大而增大，但本文主要分析截面均匀温差设计值，为在相同条件下比较截面均匀温差及其产生的内力，本文进行参数分析时只改变管径而不改变桥梁跨径。

3 计算结果分析

3.1 计算合龙温度

通过有限元计算和式(1)得到不同环境温度下的计算合龙温度。为讨论简洁，将研究对象置于福建省漳州市环境温度下称为算例1；置于四川省雅安市环境温度下称为算例2；置于河南省南阳市环境温度下称为算例3。

图2为不同算例的计算合龙温度公式值和理论值。从图中可以看出，计算合龙温度公式值和理论值有一定的误差，其原因在于式(1)忽略了不同区域环境温度变化幅度、太阳辐射和风速等次要因素对计算合龙温度的影响。不过，最大误差仅为1.0℃。

图2 不同环境温度下计算合龙温度公式值与理论值对比

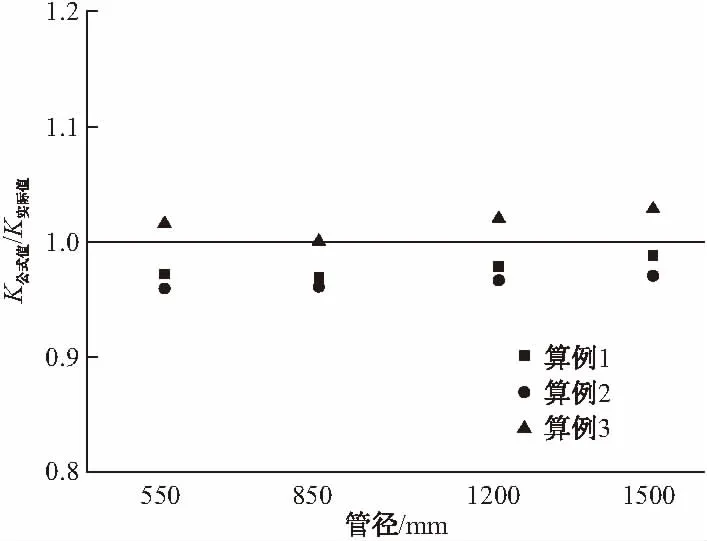
图3 合龙温度计算精度

对公式进行精度分析，计算结果见图3。图中横坐标为管径，纵坐标T公式值/T理论值表示计算合龙温度公式值与理论值的比值。可以看出，两者相比的差值均小于5%，比值的平均值为0.986，均方差为0.024。从下文3.3节的讨论可知，误差对温度次内力的影响也很小。这说明，管内混凝土浇筑后28 d的平均气温能很好反映环境温度在管内混凝土达到设计强度过程中对合龙温度的影响程度。因此，式(1)对于不同温度环境具有相当好的适应性。换句话说，式(1)可用于全国各地的钢管混凝土拱桥的计算合龙温度的计算。

3.2 有效温度

有效温度主要考虑大桥建成后相当长的运营期间内拱肋截面的平均温度值，其影响最主要的因素是当地环境温度，次主要的因素是管径大小和太阳辐射。

3.2.1最高有效温度

最高有效温度分析时，从各个区域实测8月份气象资料中，选择持续高温的最不利天气情况进行计算，计算结果见图4。可以看出，不同地区气温变化、太阳辐射和风速的差异对最高有效温度有一定的影响，但总体上截面最高有效温度均接近当地最高温度，而与日平均气温相差较大。

现行通规[1]是按钢桥面板钢桥、混凝土桥面板钢桥、混凝土和石桥三个分类，分别给出在严寒地区、寒冷地区和温热地区的有效温度标准值。三个气温分区最高有效温度均取相同，分别为按钢桥面板钢桥为46℃、混凝土桥面板钢桥为39℃、混凝土和石桥为34℃。从图4可知，对于算例1和3，最高有效温度按照混凝土桥面板钢桥取值相对接近理论值；对于算例2，最高有效温度按照混凝土、石桥取值相对接近理论值，因此无法按照通规的同一分类取值。

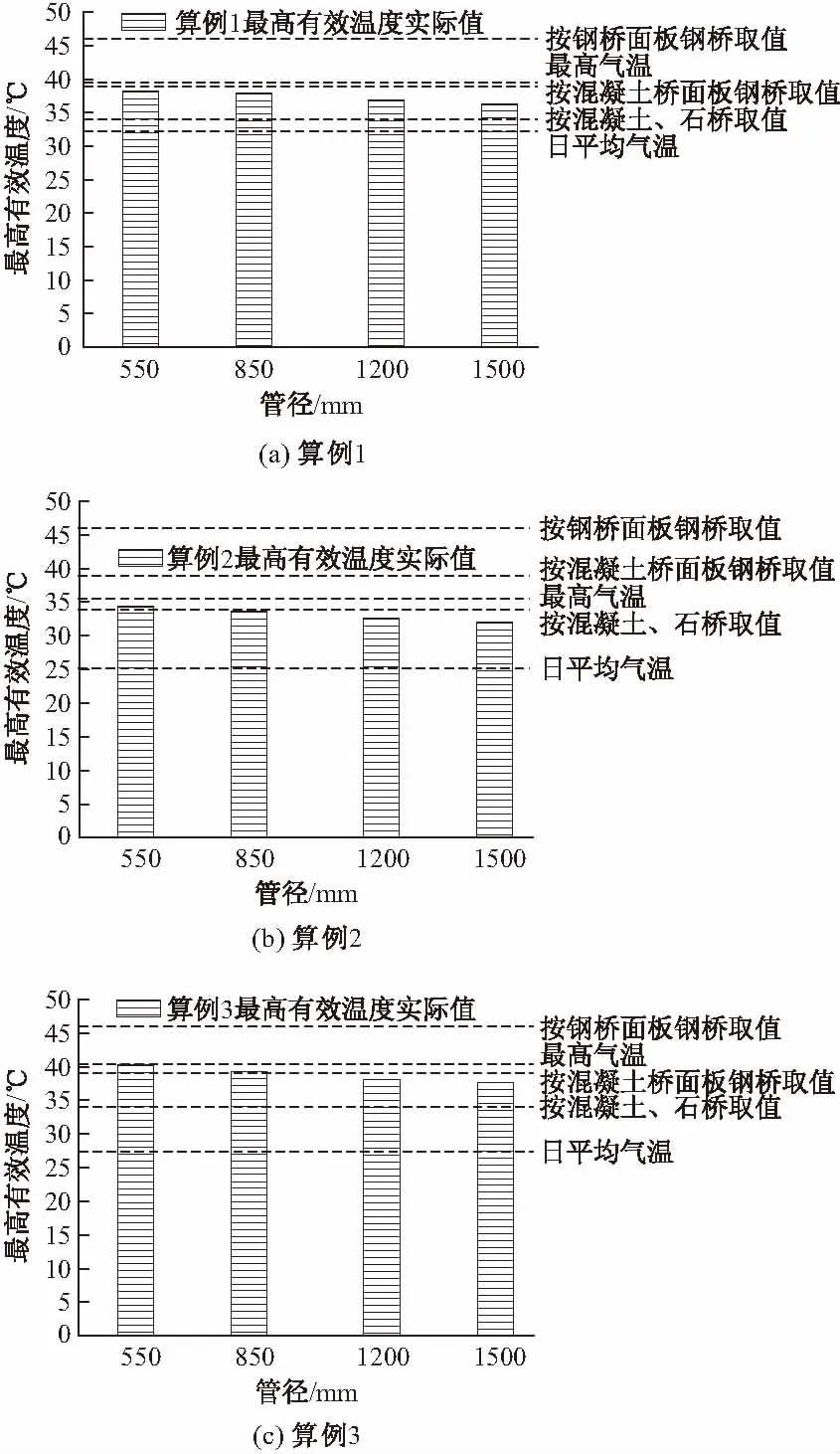
图4 不同环境温度下最高有效温度与最高气温、日平均气温及通规取值对比

最高有效温度均低于当地最高温度，对最高有效温度与当地最高温度差值Δt进行精度分析，结果见表2。可以看出，算例1中管径为1500 mm时两者差值Δt最大，为3.13℃，其原因在于：有效温度的主要影响因素之一是管径的大小，当管径较大时，混凝土所占比例越大，对环境温度的反映越缓慢，越接近钢筋混凝土结构的效应。该差值对温度次内力的影响将在3.3小节进行讨论。

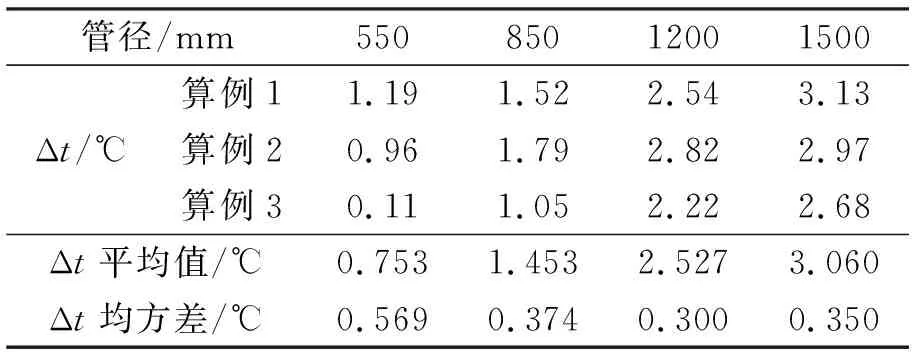
表2 最高有效温度取值精度

注：表中Δt=t2-t1，t1为最高有效温度，t2为当地最高气温。

3.2.2最低有效温度

最低有效温度分析时，从各个区域实测1月份气象资料中，选择持续低温的最不利的天气情况进行计算，计算结果见图5。可以看出，在不同地区，截面有效温度均较接近日平均气温，与最低气温及通规取值均相差较大。

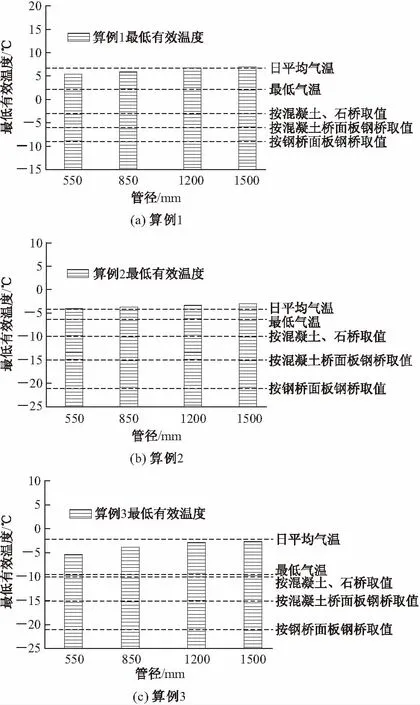
图5 不同环境温度下最低有效温度与最低气温、日平均气温及桥规取值对比

最低有效温度在日平均气温线上下浮动，对最低有效温度与日平均气温差值Δt的绝对值进行精度分析，结果见表3。可以看出，算例3中管径为550 mm时Δt最大，为3.14℃，其原因在于：算例3的气温变化较为剧烈，温差大，当管径较小时，截面越小，对环境温度的反映越迅速，截面温度场滞后相对不明显，越接近钢结构的效应。该差值对温度次内力的影响将在下节进行讨论。

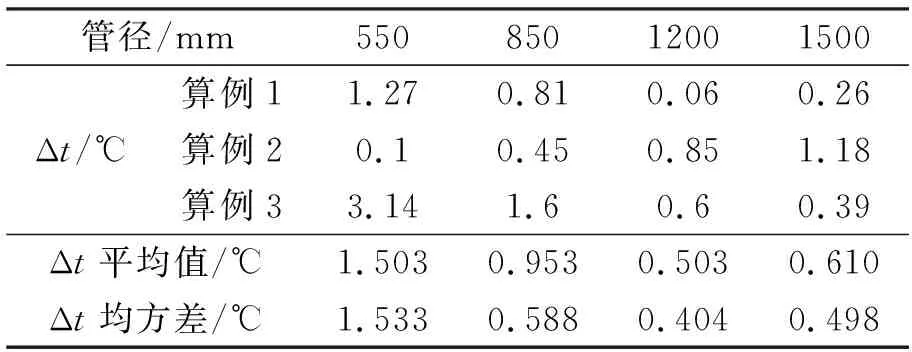
表3 最低有效温度取值精度

注：表中Δt=|t2-t1|，t1为最低有效温度，t2为日平均气温。

3.3 温度次内力比较

钢管混凝土拱桥主拱肋多为超静定结构，随着结构均匀温度的变化，由于多余约束的存在而产生温度次内力。由于我国地域辽阔，气候差异性大，影响气温的因素众多，因此气温波动大，截面温度难以准确计算。钢管混凝土拱截面均匀温差设计值取值考虑了环境温度和管径这两个最主要因素，因此设计值与计算值存在一定的误差。本小节将对均匀温差设计值误差产生的温度次内力进行比较以对取值的合理性进行讨论。

对实桥进行有限元计算可知，拱截面平均温度上升1℃产生的温度次内力见表4。由于是均匀温度变化，因此温度下降1℃的次内力绝对值与温升相同，只是两者的符号相反。

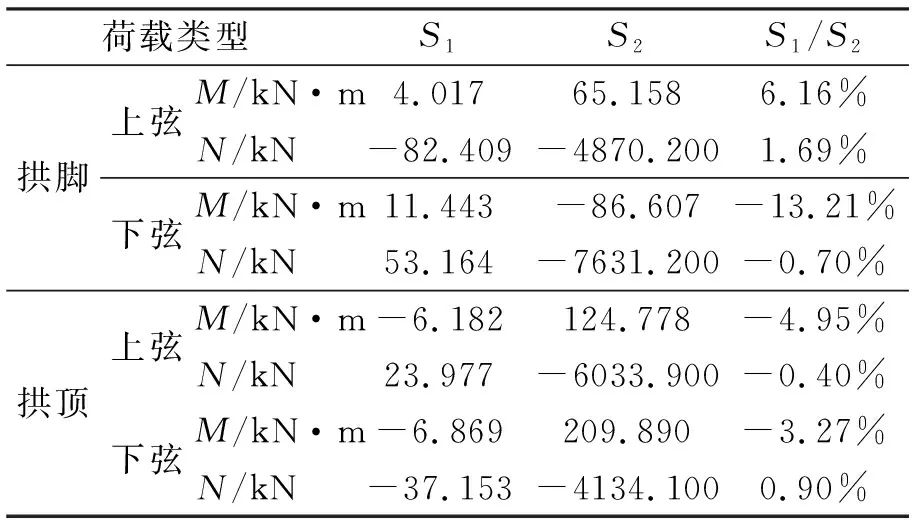
表4 结构温升1℃的次内力与桥梁自重内力的比较

注：表中S1为结构温升1℃的次内力，S2为桥梁自重内力。

拱桥是以受压为主的结构，因此主要讨论其轴力的大小。从表4可以看出，升温1℃以拱脚上弦温度次内力占桥梁自重内力的比重最高，为1.69%，在下文的分析中，将温差乘以该比值就可以得到温差产生的温度次内力占桥梁自重内力的比重，以此说明截面均匀温差设计取值误差对桥梁内力的影响。

3.3.1计算合龙温度

拱桥均匀温度作用常以温降为控制，因此在分析计算合龙温度取值中以降温产生的温度次内力作为分析对象。

对三个地区计算合龙温度取值差值产生的温度次内力占桥梁自重内力的比重进行计算，结果见表5。可以看出，按照式(1)进行取值的误差产生的温度次内力占桥梁自重内力的比重均在2%以内。由前文分析可知，计算合龙温度公式值和理论值最大误差为1.0℃，误差平均值为0.37℃；而如果按照3.2节有效温度取值方法，其最大误差为3.14℃，误差平均值为1.41℃。计算合龙温度的取值精度远高于有效温度。桥梁设计中结构受到的(均匀)温度作用是通过最高和最低有效温度与结构的位移受到约束时的温度(基准温度)之差计算的，由计算合龙温度和有效温度共同决定。因此，建议将其作为计算合龙温度设计值，而对有效温度进行保守取值。

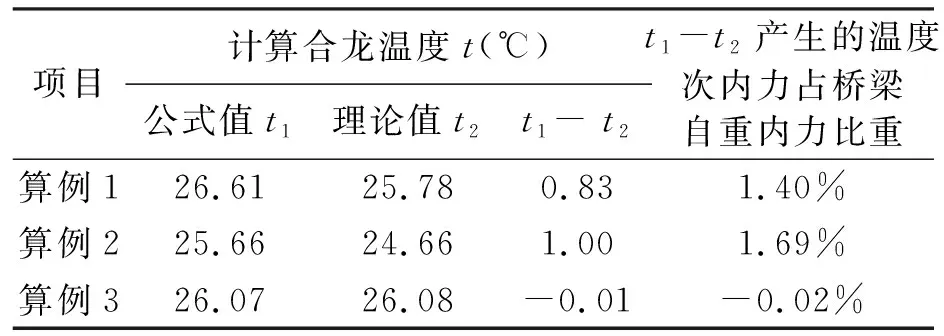
表5 计算合龙温度取值对比

3.3.2最高有效温度

为了研究最高有效温度取值方法，表6分别按照最高气温、最高日平均气温和通规中的相关规定进行最高有效温度取值，计算合龙温度采用理论值，计算并比较不同取值的温度次内力占桥梁自重内力比重。从表中可以看出，如果按通规的规定取值，算例1和3按照混凝土桥面板钢桥取值与实际值较为接近；算例2按照混凝土、石桥取值与理论值较为接近。如果按照最高气温取值，温度次内力占桥梁自重内力比重与理论值的差值均在5%以内，且偏于保守。

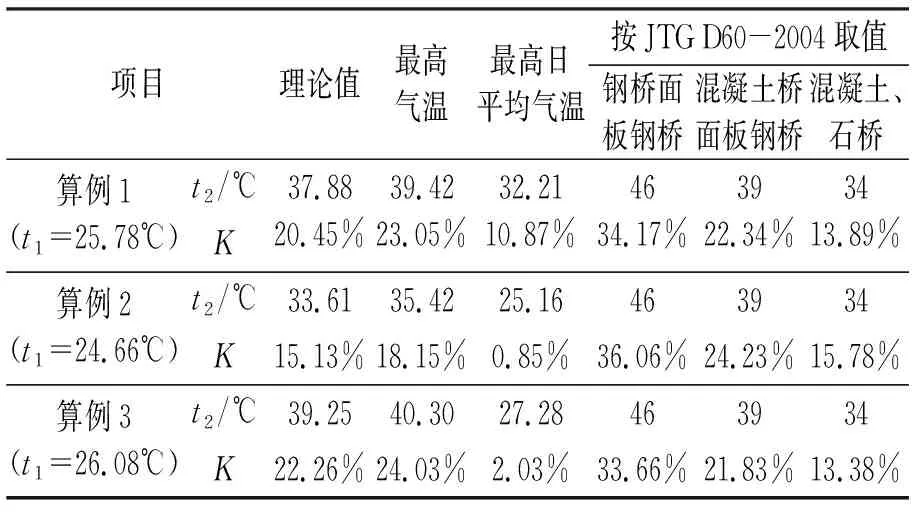
表6 最高有效温度取值对比

注：表中K为温度次内力占桥梁自重内力比重，t1为计算合龙温度，t2为最高有效温度。

由于在本文气象观测期内并未出现历史极端气温，因此查询了中央气象局不同地区极端气温资料(时间跨度：1951年01月01日～2008年12月31日)，相关数据见表7。可以看出，三个地区历史最高气温与本文观测值相差小于3℃，温度次内力占桥梁自重内力比重小于5.07%。因此基于本文观测的最高温度数据分析结果具有代表性，最高有效温度建议取当地最高气温。

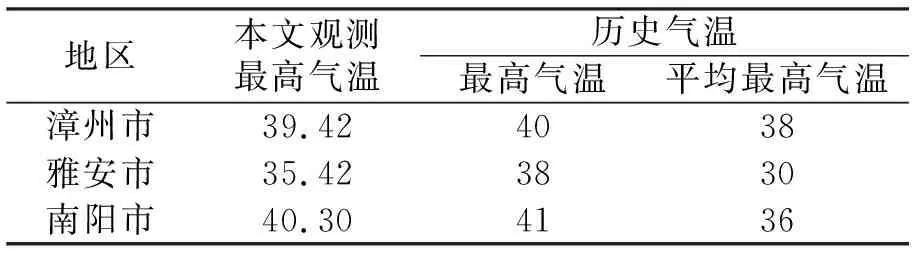
表7 最高气温对比 ℃

3.3.3最低有效温度

采用与最高有效温度同样的研究方法分析最低有效温度取值。表8分别按照最低气温、最低日平均气温和通规进行最低有效温度取值，且通规中的最低有效温度根据不同地区所属的气温分区取值。从表中可以看出，如果按通规取值，温度次内力与理论值相差较大。如果按照日平均气温取值，温度次内力占桥梁自重内力比重与理论值的差值均在5%以内。

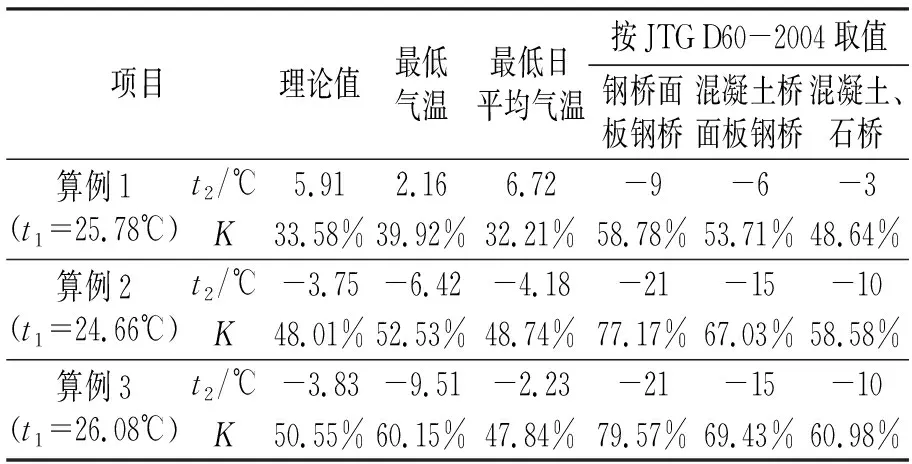
表8 最低有效温度取值对比

注：表中K为温度次内力占桥梁自重内力比重，t1为计算合龙温度，t2为最高有效温度。

查询中央气象局不同地区历史极端气温资料，相关数据见表9。可以看出，雅安、漳州地区历史极端最低气温与本文观测值相差小于5℃，且其历史平均最低气温均高于本文观测到的最低气温，由前文关于钢管混凝土截面温度场特性可知，其截面温度差值小于5℃，温度次内力占桥梁自重内力比重小于8.45%。对于南阳地区，历史极端最低气温(出现在1955年)与本文观测值相差12℃，但是其历史平均最低气温只有-5℃，可以认为该极端气温只是短暂出现，并且根据钢管混凝土截面滞后特性及通规对可变作用乘以1.4分项系数的规定，因此基于本文观测数据的分析结果具有代表性。建议取日平均气温作为最低有效温度。考虑到一般设计人员不易得到最低日平均气温，因此偏保守考虑，可以取当地最低气温作为最低有效温度。

表9 最低气温对比 ℃

4 结 语

以一座钢管混凝土桁拱为研究对象，采用有限元软件ANSYS，进行了钢管混凝土拱截面均匀温差设计值取值研究，得到以下结论：

(1)应用从我国三个不同地区采集到的环境温度资料进行计算分析，讨论了DBJ/T13-136-2011中计算合龙温度取值方法精度及其温度次内力与理论值的差异。结果表明，公式取值精度较高，最大差值为1℃，产生的温度次内力占桥梁自重内力的比重为1.69%，建议将其作为计算合龙温度设计值，DBJ/T13-136-2011中计算合龙温度取值方法可以推广到全国范围。

(2)根据极端气温、日平均气温和JTG D60-2004中的相关规定进行有效温度取值，计算并比较误差产生的温度次内力占桥梁自重内力的比重。分析表明，对于最高有效温度，按照最高气温取值，温度次内力占桥梁自重内力比重与理论值的差值均在5%以内，且偏于保守。建议取当地最高气温作为最高有效温度。对于最低有效温度，按照最低日平均气温取值，温度次内力占桥梁自重内力比重与理论值的差值均在5%以内。建议取日平均气温作为最低有效温度。考虑到一般设计人员不易得到最低日平均气温，因此偏保守考虑，也可以取当地最低气温作为最低有效温度。

[1] JTG D60-2004，公路桥涵设计通用规范[S].

[2] 陈宝春, 徐爱民, 孙 潮. 钢管混凝土拱桥温度内力计算时温差取值分析[J]. 中国公路学报, 2000, 13 (2): 52-56.

[3] 林春姣．钢管混凝土拱计算合拢温度研究[D]. 广西: 广西大学, 2007.

[4] 范丙臣．中承式钢管混凝土拱桥的温度评价及试验研究[D]. 哈尔滨: 哈尔滨工业大学，2001.

[5] 彭友松, 强士中, 李 松. 哑铃形钢管混凝土拱日照温度分布研究[J]. 中国铁道科学, 2006, 27 (5): 71-75.

[6] 柯婷娴, 陈宝春, 刘振宇. 日照下钢管混凝土哑铃形拱肋截面的温度场有限元计算[J]. 长沙交通学院学报, 2008, 24 (4): 12-17.

[7] 陈宝春, 刘振宇. 日照作用下钢管混凝土桁拱温度场实测研究[J]. 中国公路学报, 2011, 24 (3): 72-79.

[8] DBJ/T13-136-2011，钢管混凝土拱桥技术规程[S].

[9] 黄福云, 陈宝春, 柯婷娴. 钢管混凝土哑铃形拱的计算温度取值研究[J]. 福州大学学报(自然科学版), 2011, 39 (2): 266-275.

[10]Tang S, Cai W, Chen B. A Half-through Rigid-frame Tied CFST Arch Bridge with Two Cantilever Concrete Deck Arches——Xiyangping Bridge in Zhangzhou. China[C]//Proceedings of the Fifth International Conference on Arch Bridge. 2007: 12-14.

[11]刘振宇, 陈宝春. 钢管混凝土桁拱热脱粘及温度应力分析[J]. 公路交通科技, 2011, 28 (7): 67-72.

[12]马庆芳, 方荣生, 项立成. 实用热物理性质手册[M]. 北京: 中国农业机械出版社, 1986.

[13]西格尔R, 豪厄尔J R. 热辐射传热[M]. 曹玉璋, 黄素逸, 陆大有, 等译. 北京: 科学出版社, 1990.

[14]刘振宇, 陈宝春. 钢管混凝土拱肋施工过程截面温度特性分析[J]. 公路交通科技, 2006, 23 (5): 52-55.

[15]王铁梦. 工程结构裂缝控制[M]. 北京: 中国建筑工业出版社, 1997.

[16]陈宝春. 钢管混凝土拱桥(第2版)[M]. 北京：人民交通出版社, 2007.