弹塑性海床上海底管道的稳定性分析

(北京建筑工程学院 理学院，北京 100044)

波浪引起的水动力载荷是作用在海底管道上的最主要的动力荷载，而海床土壤提供给管道的侧向阻力是管道得以稳定的主要因素。海底管道的稳定是一个波浪、管道和海床之间动力耦合作用的复杂问题，研究管土相互作用，正确评价土体对管道阻力的作用，对于确保管道的稳定性、安全性和经济型，对于完善有关设计规范都有着重要的意义。

20世纪80年代以来，国外许多科研机构采用机械式反复加载的方式深入研究了裸置管道的管土相互作用，并提出了管土相互作用模型。这些结论已归结到“美国天然气协会”和“挪威船级社”所制订的海底管线的稳定性设计规范中[1-5]。许多学者在数值模拟方面做了许多研究工作[6-7]。本文采用有限元计算软件对管土系统进行数值模拟。

1 土体本构模型

由于管道是设置在海洋环境中，波浪引起的载荷性质为动态的。因此，采用Ramberg-Osgood弹塑性模型作为土体的本构关系。土性参数见表1。应力-应变关系的骨干曲线为

(1)

式中：E——弹性模量；

ε——应变；

σ——应力；

σ0——屈服应力；

n——非线性项的硬化参数；

α——屈服偏移量。

表1 土性参数

2 有限元模型

在数值计算中，将管道视为线弹性材料，其弹性模量、泊松比分别为E=210 GPa，v=0.3。管道用8节点单元，海床用4节点单元，考虑到管线周围的应力集中，在管线及其附近采用了局部加密网格。有限元模型见图1。

2.1 管-土接触效应

在海床-管线的相互作用分析中，当有荷载作用时，海床土体与管线交界面上可能产生剪切滑移，因此需要设置接触面单元。在ABAQUS的接触模拟中，采用了约束函数接触算法。在计算时，为真实地模拟实际接触面上的相互作用效应，选择管线外表面为主接触面，与管线相接触的海床土体为从属接触面，两者形成一个接触对。根据Coulomb 摩擦理论计算海床-管线间的摩擦切应力管-土接触效应见图2。

图1 有限元模型示意

τ=μpc

(2)

式中：μ——摩擦因数，本文取μ=0.7；

Pc——两接触面上的接触压力。

图2 管-土接触效应示意

2.2 载荷的施加和边界条件

管土模型受到的主要荷载有管道的自重和波浪产生的动荷载。将所受的渗流力简化成一对正弦变换的面荷载施加在海床模型两侧，以模拟波浪对海床和管道的作用，并忽略模型上表面的剪切力。

在结构-地基动力相互作用问题的动力数值模拟中，不可能将整个地基都包括，计算时只能截取一定的范围，只考虑截断边界以内的部分。通过对比计算，海床的计算范围水平方向为管径的20倍，垂直方向为管径的10倍。为了保证运动波能够通过截断边界而不被反射，需要在截断边界施加人工边界条件。管线-海床的相互作用问题可看作是结构-地基动力相互作用问题的一类。边界条件为：远离管道的边界上，海床的左右两侧及底部为固定边界，而海床的上边界为自由边界，无约束。

2.3 有限元模型验证

为了验证模型的合理性，将多孔模型孔隙水压力的计算结果与文献的试验结果进行比较。图3为管周8个节点处的孔隙水压力最大值的绝对值|p|与海床面波压幅值p0的比值结果。

该试验用土为匀质土，分别为粗砂和细砂。由图3可看出，本文计算结果与文献结果吻合，验证了本文计算模型的适用性。

3 结果分析

为探讨管线周围由于波浪载荷作用所引起的位移分布，针对各种影响因素，分别变动管径、管重、环境载荷等参数进行对比计算，采用半动态分析计算方法。

3.1 位移场的影响

当管道外径D=1.0 m,管道水下重为Ws=11.8 kN/m时，通过数值计算绘出管道的水平位移等值线图、垂直位移等值线图，见图4、5。

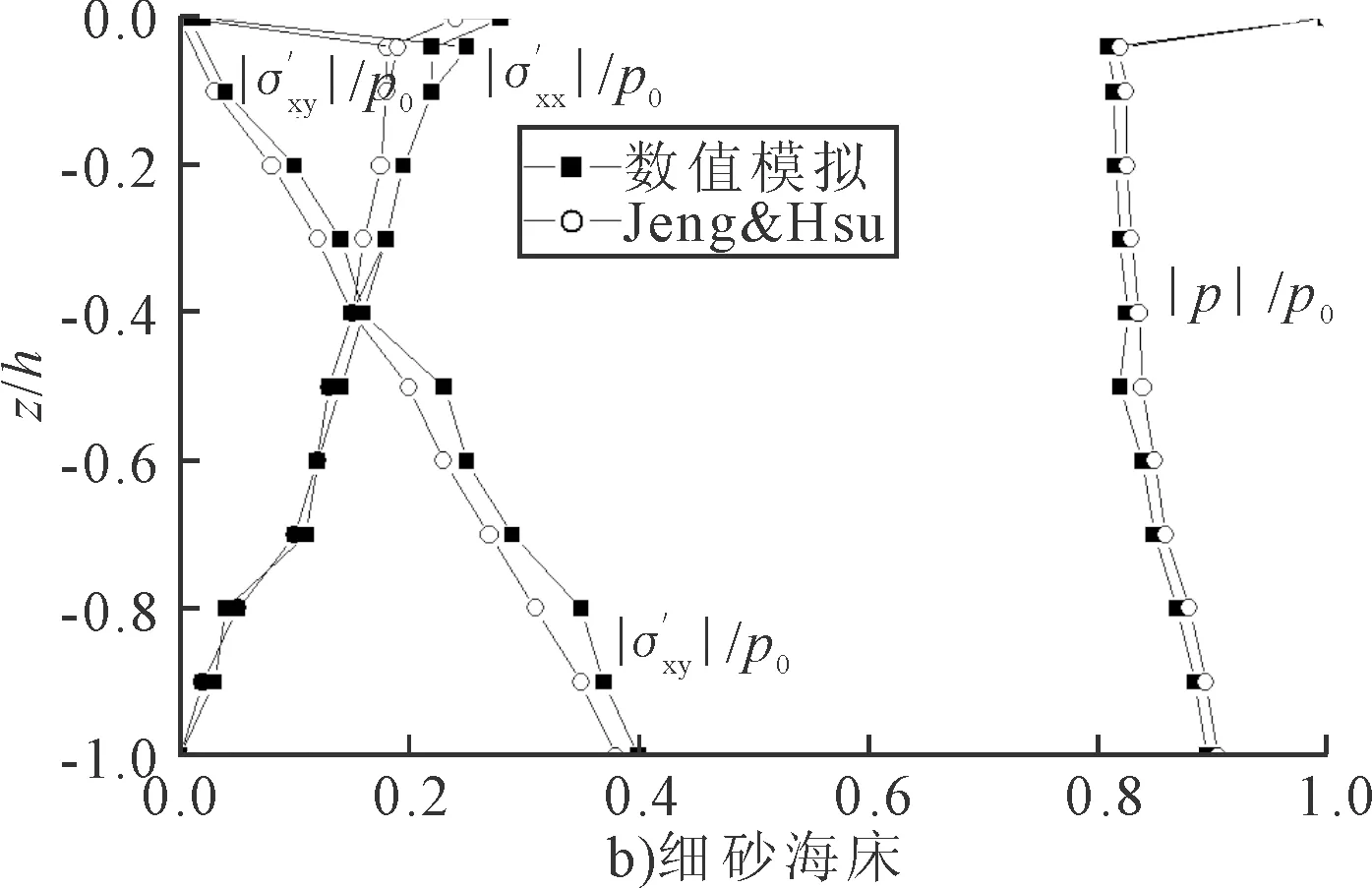
图3 孔隙水压力和有效应力

图中：z/h为所求应力点处的深度与海床深度的比值。

图4 管土系统水平位移等值线示意

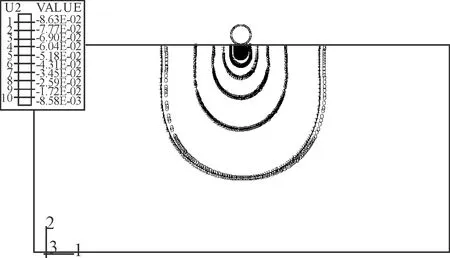
图5 管土系统垂直位移等值线示意

从图4、5可以发现，靠近管道处，土体的垂直位移较大，随着海床深度和宽度的增加，垂直位移逐渐减小，最后变为零。而水平位移等值线图的位移等值线并不只是集中在靠近管道处，而是有一部分等直线已经扩展到了海床的边缘附近。由此可见，远离管道的土体受外载荷的影响较小。

3.2 管重的影响

保持环境参数不变，当管径为0.4、1.0 m时，可以得到管道的沉降量、接触面的摩擦力与管道水下重间的关系如见图6～10。

图6 管道水下重力对沉降量的影响

图7 总沉降量与管道水下重力间的关系

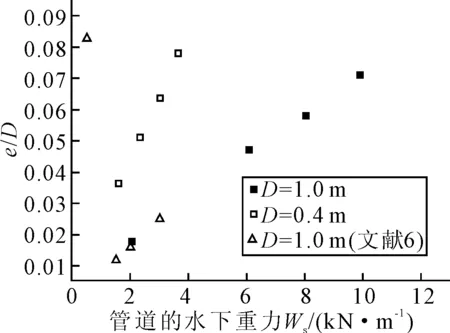
图8 管道沉降量与试验的比较

图9 摩擦力与管重的关系

由图6知，管道自沉降随管重力的增加而增加，而附加沉降随管重力的增加而减小，但总的沉降量随管重力的增加而增加，见图7。原因是随管道水下重力的增加，自沉降增加，导致作用在管道上的环境载荷减小，土体中附加应力很小，管土系统趋于稳定状态，则附加沉降不会增加。由图8知，管道沉降量的计算结果与试验结果[8]相比吻合。由图9知，管道所受的摩擦力随着管重的增加呈现减小的趋势，这是因为随着管重的增加，管道的沉降量在增加，土体的侧向阻力在增大，则相应的摩擦力就减小。图10表明，水平位移开始随着管重的增加而减小，但是当管重增加到一定数值，在8.305 kN/m时，却随着管重的增加而增加，这是因为随着管重的增加，土体中的附加应力(3.8×104Pa)增大，超过屈服应力(3.0×104Pa)，因此土体中的单元会发生破坏，从而管道的水平位移增加。

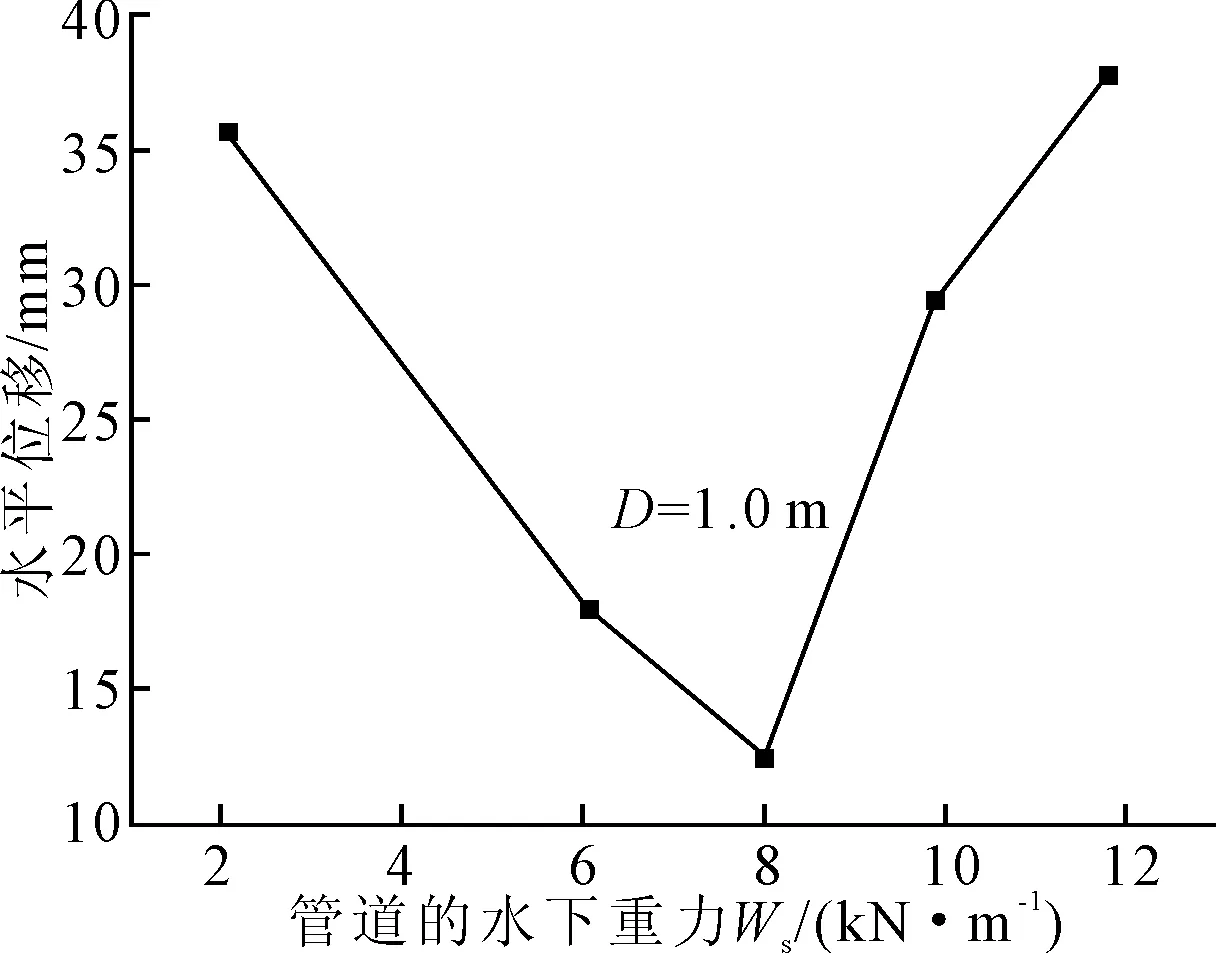
图10 水平位移与管重间的关系

3.3 环境载荷的影响

保持管道水下重不变，改变环境参数进行计算，所得结果见图11～13。

图11 沉降量与环境载荷的关系

图12 水平位移与环境载荷间的相对关系

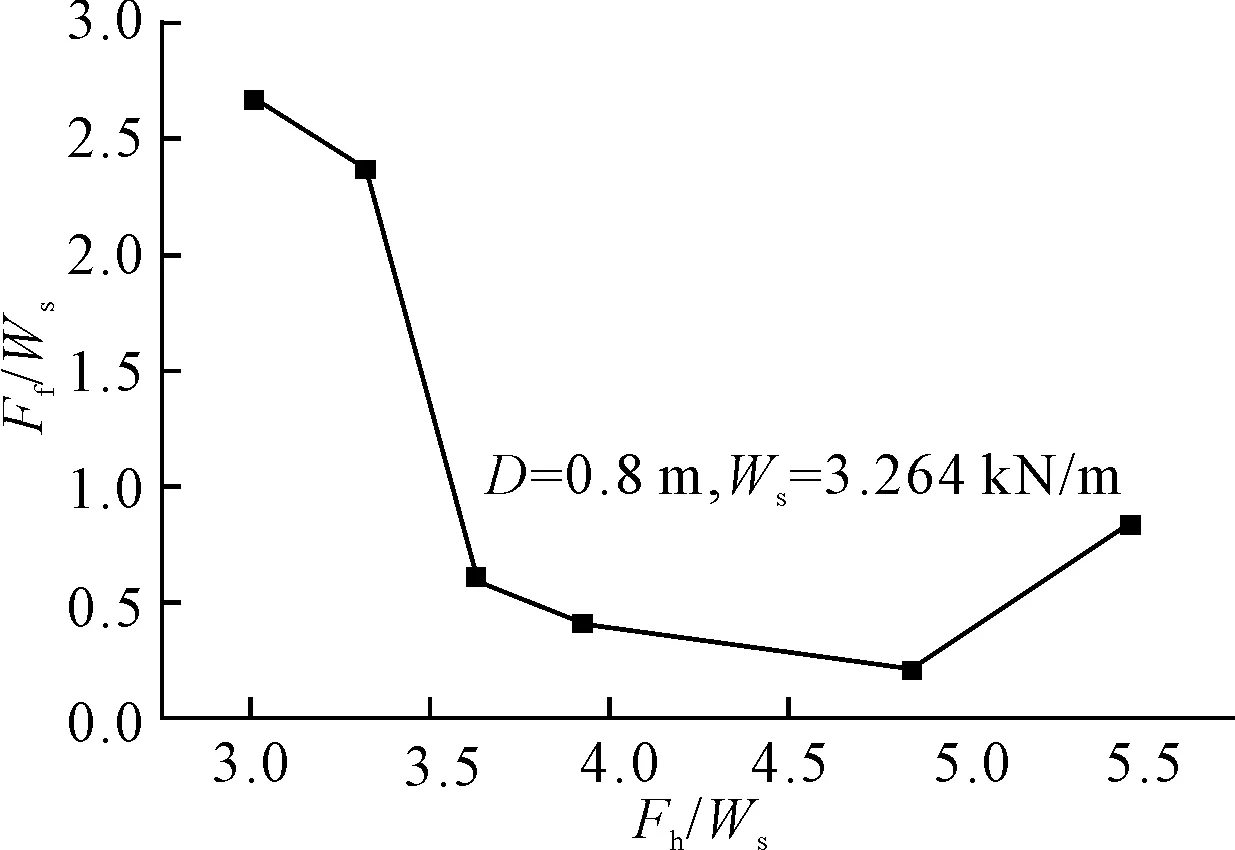
图13 摩擦力与环境载荷间的相对关系

图中：Fh/Ws——环境载荷与管重的比值；

Ff/Ws——摩擦力与管重的比值；

z/D——沉降量与管径的比值；

H/D——水平位移与管径的比值。

由图11、12知，随着作用在管道上的环境载荷的增大，土体中的附加应力增大，因此管道的最终沉降量在增大，水平位移也在增加。从图13知，摩擦力与管重的比值随环境载荷的增加而减小，这是由于流体动力载荷的增大，管道的沉降量在增加，则土体施加给管道的侧向阻力增大，相应接触面上的摩擦力则减小。

3.4 管径的影响

保持管道的水下重不变，即Ws=3 kN，环境条件不变，改变管径进行计算，结果见图14～16。

由图14～16可见，随着管径的增加，管道的沉降量，水平位移，摩擦力都在增加。

图14 沉降量与管径的关系

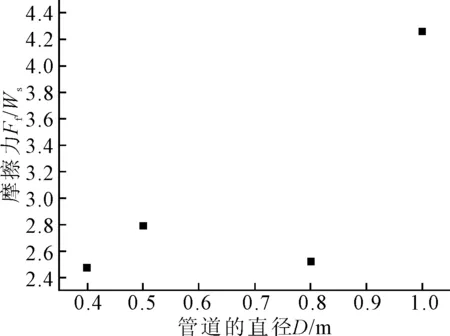
图15 摩擦力与管径的关系

图16 水平位移与管径的关系

3.5 屈服应力的影响

对于塑性模型，只要土体单元的应力超过了屈服应力，则土体就会进入屈服状态，从而引起破坏。因此在数值模拟时，研究了屈服应力对管道的沉降量的影响，所得结果见图17。

图17 沉降量与屈服应力的关系

由图17可见，随着屈服应力的减小，管道的沉降量在增大。这是由于屈服应力越小，土体中某些单元的应力就会越容易达到屈服点，从而导致土体的某个部分发生破坏，因此造成管道的沉降量增大。

3.6 管道的侧向阻力

保持管道的水下重不变，改变其环境条件，从而得到管道上的总的极限阻力随沉降量的变化情况。同时，观察管道与土体之间的接触面的变化情况，得到摩擦力、侧向阻力和阻力系数随管道的沉降量的变化情况，其结果见图18～20。

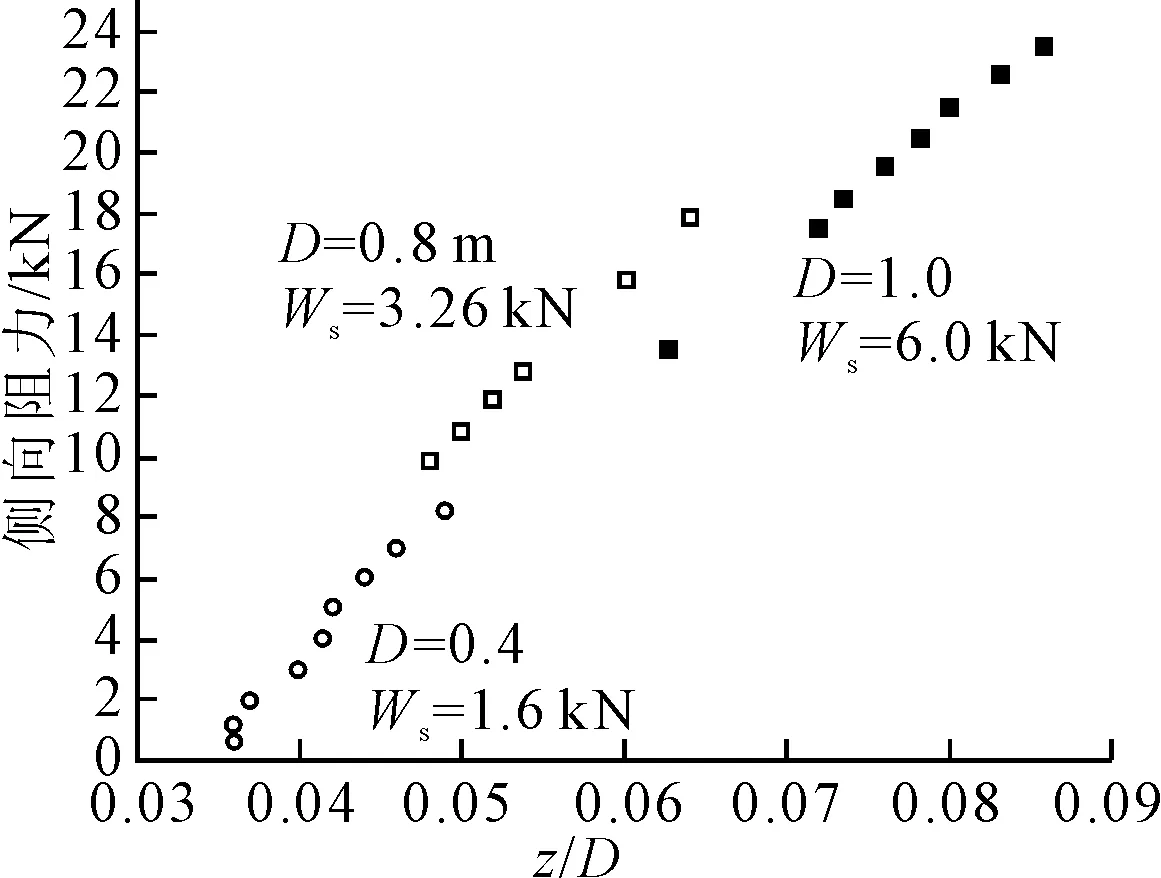
图18 极限阻力与沉降量间的关系

由图18可见，管道的水下重，管道的直径以及管道的沉降量等几个因素影响管道的极限水平阻力，并且可以看出，随着管道相对沉降量的增加，极限阻力也在增大。由图19可见，随着作用在管道上环境载荷的增加，管道的沉降量在增大，所引起土体的侧向阻力增大，因此管道和土体之间的接触面上的水平方向的摩擦力在减小。由图20可见，阻力系数随管道的相对沉降量的增加而增加，这是因为作用在管道上土体的阻力在增大。

图19 摩擦力与沉降量间的关系

图20 阻力系数与沉降量间的关系

4 结论

1)由于实际海床土体是一种弹塑性材料，受力后既有弹性变形，又有塑性变形；加之所受的外载荷为动态的，因此采用Ramberg-Osgood弹塑性模型作为土体的本构关系进行计算。

2)用有限元方法进行管道沉降量的计算是可行的，同时也表明管道水下重、环境载荷、管径、

屈服应力等对管道的沉降量、摩擦力、极限阻力、阻力系数均有不同程度的影响。

[1] H BRENNODDEN,O SVEGGEN.Full-scale pipe/soil interaction tests[C]∥ Proceedings of Eighteenth Annual Offshore Technology Conference,Ganada,Saint John City： OTC Paper 5338,1986:433-440.

[2] D A WANGER,J D MURFF,H BRENNODDEN.Pipe-Soil Interaction model[C]∥ Proceedings of Nineteenth Annual Offshore Technology Conference,Houston: OTC paper 5504,1987:181-190.

[3] A C PALMER.Lateral Resistance of Marine Pipelines on Sand[C]∥ Proceedings of 20th Annual Offshore Technology Conference,Houston: OTC Paper 5853,1988:399-408.

[4] D W ALLEN,W F LAMMERT.Submarine Pipeline On-Bottom Stability:Recent AGA Research[C]∥ Proceedings of 21st Annual Offshore Technology Conference,Houston: OTC Paper 6055,1989:121-132.

[5] J R HALE,W F LAMMERT.Pipeline On-bottom Stability Calculations:Comparison of two state-of-the art methods and pipe-soil Verification[C]∥ Proceedings of 23rdAnnual Offshore Technology Conference,Houston: OTC Paper 6761,1991: 567-581.

[6] GAO F P,JENG D S,SEKIGUCHI H.Numerical Study on the Interaction between non-Linear Wave,Buried Pipeline and non-Homogeneous Porous Seabed[J].Computers and Geotechnics,2003,30(6):535-547.

[7] GAO F P.WU Y X.Non-Linear Wave-Induced Transient Response of Soil around a Trenched Pipeline[J].Ocean Engineering,2006,33(3-4):311-330.

[8] H BRENNODDEN,J T LIENG,T SOTBERG,et al.An energy-based pipe/soil interaction model[C]∥ Proceedings of 21st Annual Offshore Technology Conference[C]∥ Houston: OTC Paper 6057,1989:147-158.