三维矩形弹性液舱内液体晃荡数值模拟研究

，

(大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116023)

液体晃荡是极为复杂的一种流体运动形式，它具有高度的非线性和随机性。在以往的研究中，液体晃荡问题大部分的研究工作主要集中在刚性液舱数值模拟方面[1-3]，然而实际工程中所使用的液舱都有一定的弹性，假定液舱是刚性结构，忽略了液舱结构的变形，同时也忽略了液舱变形与内部流体的相互作用。近年来有部分学者对弹性液舱的液体晃荡问题进行了一些研究[4-6]，对于弹性液舱晃荡，必须研究晃荡过程中带自由液面流体的非线性动力学问题及其结构变形的相互耦合问题。

1 数值方法

假设矩形液舱为线弹性结构，液体为不可压缩的粘性流体。流固耦合接触面上，流体和结构不直接脱离，即流体与结构在接触面上任意时刻法向位移都相等。

采用有限元法对流体域连续方程、运动方程、质量守恒方程等进行离散求解；采用隐式积分法对结构域几何方程、运动方程、物理方程等进行积分求解[6]。

ADINA在求解流固耦合问题时有直接耦合求解和迭代耦合求解。本文采用直接耦合法进行计算，将流体域、结构域和耦合作用构造在同一控制方程——流固耦合系统方程中，在单一时间步内，对流固耦合系统方程所有变量同时进行求解。采用位移-压力格式描述流固耦合系统。

流固耦合系统方程为

(1)

式中:X——耦合系统的解向量，X=(Xf,Xs)。

其中：Xf,Xs——定义在流体和结构节点上的解向量。

因此流固耦合面上结构的位移和流体应力分别表示为ds=ds(Xs)，τf=τf(Xf)。Ff,Fs分别是流体与结构相应的有限元方程。

对于单独的流体或结构模型来说，其线性方程如下。

1)流体方程。

(2)

2)结构方程。

(3)

将流体方程和结构方程放在一个方程组中

(4)

流体应力和结构位移分别使用了应力松弛因子λτ(0<λτ<1)和位移松弛因子λd(0<λd<1)。

计算过程概括如下：设初始解0X=tX。对k=1，2，进行迭代，求t+Δt时刻的解t+ΔtX。

分别整理流体方程和结构方组，得到耦合的方程组。

求解耦合系统的线性方程组并更新得到的解。计算应力和位移残量并和给定的迭代容差比较。如果解还是不收敛，且没有达到FSI迭代的最大次数，则回到第一步继续下一个迭代，否则，程序停止并显示不收敛的信息。

保存并输出流体和结构的结果。

2 模型建立与验证

2.1 模型建立

采用有限元软件ADINA分别建立三维矩形刚性模型与对应的弹性模型。

2.1.1 三维刚性液舱模型

矩形液舱计算模型示意见图1。

图1 ADINA液舱计算模型示意

模型尺寸为L=2a=0.5 m，B=2b=0.1 m，H=0.5 m，载液率r为16%和50%。

液舱厚度δ=12 mm，密度ρ=1.185×103kg/m3，泊松比ν=0.35，弹性模量E=2.1×1011Pa。流体采用自来水，粘度ν=1.005×10-3Pa·s，密度ρ=1×103kg/m3。在ADINA-Structure中建立结构模型，将结构定义为Shell 单元，设定FSI流固耦合边界条件；同时在ADINA-CFD中建立流体模型，划分为3-D fluid 单元，设定与结构对应的FSI流固耦合边界条件和自由表面边界条件，然后在ADINA-FSI中进行耦合计算，ADINA网格见图2。

2.1.2 三维弹性液舱模型

为研究液舱弹性对晃荡的影响，将模型左右侧舱壁和顶盖的壁厚改为2 mm，其余保持不变。

图2 ADINA网格

2.2 模型验证

2.2.1 液体固有频率的分析

纵荡激励下、液舱内晃荡液体的固有频率为fn。对于给定几何尺寸的液舱而言，晃荡液体的固有频率可以由Abramson线性理论公式进行估算：

(5)

式中：L——液舱长度；

h——液舱内液深；

n——模态数，n=1，2，…。

运用ADINA建立三维矩形液舱模型来计算该液舱内晃荡液体的固有频率并将其与Abramson线性公式计算结果进行比较，结果见表1。

表1 不同模态下液体晃荡固有频率 Hz

注：fElastic为2.1.2弹性模型的计算频率；fRigid为2.1.1刚性模型的计算频率。

由表1可见，刚性液舱内液体各阶固有频率与理论计算所得液体各阶固有频率非常接近；同时由于流固耦合作用的影响，当液舱为低液深时，弹性液舱内液体一阶固有频率大于刚性液舱内液体的一阶固有频率；反之当液舱为高液深时，弹性液舱内液体一阶固有频率小于刚性液舱内液体的一阶固有频率。

2.2.2 ADINA数值解与Faltinsen解析解的比较

Faltinsen针对水平激励下的二维矩形液舱内的液体晃荡，提出了一个基于势流理论的线性解析解，广泛地应用于各种数值模型的验证。本文将该解析解由二维情况扩展到三维情况[7]，可得到自由液面位移η。

(6)

(7)

采用2.1.1模型，根据2.2分析得知：载液率r为50%时,液舱内液体一阶固有频率为fRigid=1.197 Hz。给定外界激励振幅A=0.004 m，采用两种工况对A点处自由液面的波高历时曲线进行对比分析，见图3。

图3 A点处自由液面波高历时曲

由图3比较可知，采用ADINA模型计算所得到的数值解与Faltinsen解析解吻合较好，说明本文的ADINA模型有效。

3 三维弹性液舱内液体晃荡

为了验证三维弹性模型的正确性及可行性，对模型进行物理模型实验，并将结果与ADINA模型模拟结果进行对比。

将压力传感器布设在液舱的右侧舱壁上，标签“PN”代表压力传感器PN处的晃荡压力数据，N=1，2，3，…见图4。其中P1，P2，P3号压力传感器分别距离底板80、125、250 mm。本文只针对 P1，P2，P3号压力点进行了压力分析。

图4 压力传感器P布置示意

3.1 弹性液舱内晃荡液体的自由液面运动

对上述模型分别按表2各工况进行模拟，各工况激励振幅A=0.004 m。

表2 计算工况

注：fA，fE为弹性液舱内液体的一阶固有频率，且由于r=50%时，ADIAN计算模型的一阶固有频率fA=1.194 Hz与对应的实验模型一阶固有频率fE=1.090 Hz具有一定的差距，为了达到共振效果，ADINA模型采用的外界激励频率fA=1.194 Hz。

分析A点处自由液面的波高历时曲线，并且将计算结果与实验值进行对比，见图5。

图5 A点处自由液面的波高历时曲线

在数值模拟过程中观察到波面的三维情况，图6和图7中分别给出了晃荡液体模型不同时刻的三维波面图及晃荡液体模型在A和C点的波高历时曲线对比图。

图6 Case2液体模型在t=0.0、6.04、12.4及21.2 s时的三维波面图

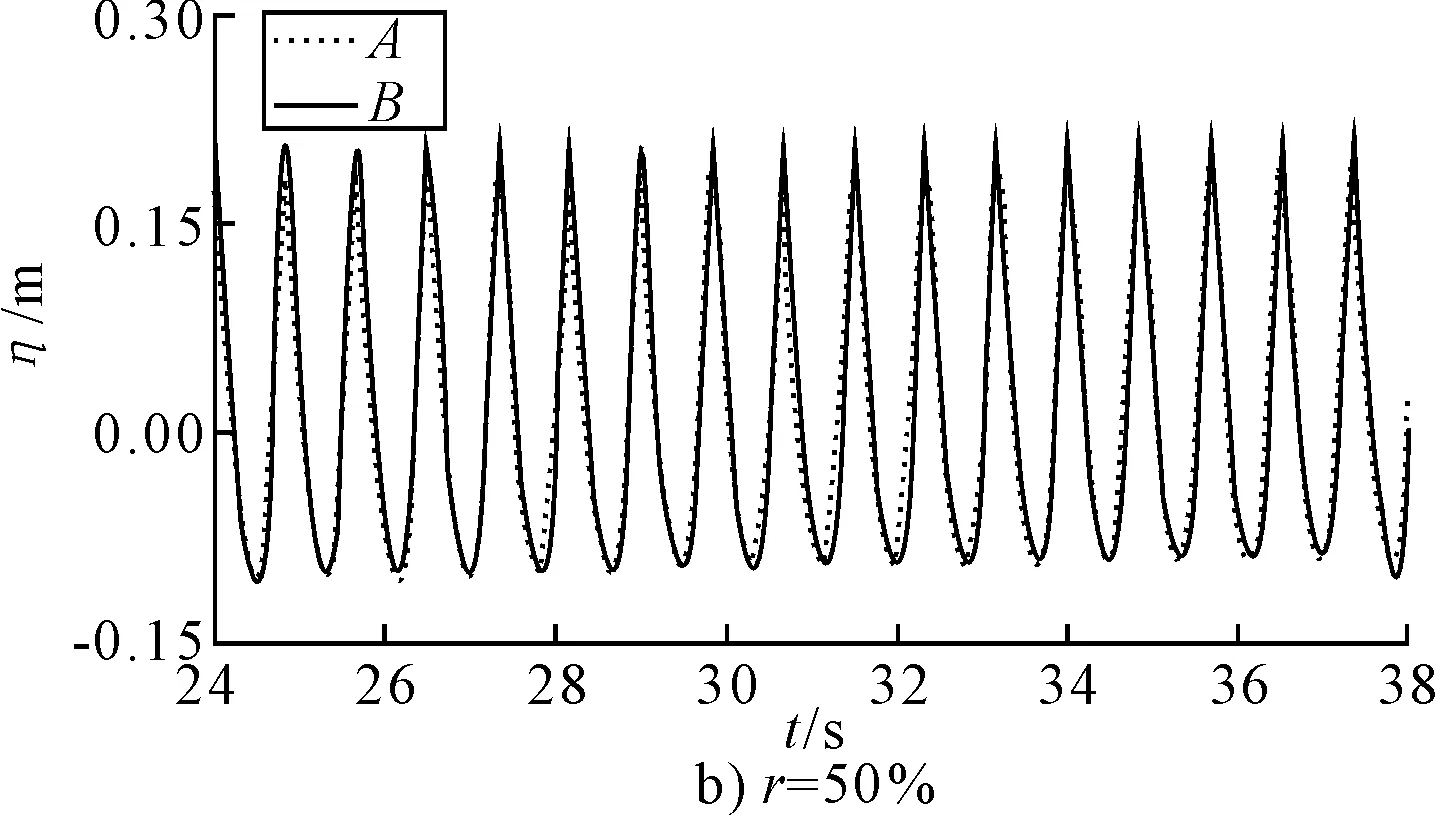
图7 A、B点处自由液面波高历时曲线对比图

综合分析图5～7，对比不同载液率液舱在共振频率下液舱晃荡自由液面波高历时曲线及波面图可以得出以下结论。

1)从图5～7可见，基于有限元数值模拟软件ADINA的数值模拟结果与实验值基本吻合，验证了弹性模型的有效性。

2)从波高历时曲线图5中可以看出，液舱内液体晃荡剧烈，液体在壁面形成爬高。图5a)和图5b)分别为低、高液深时A点处波高历时曲线，从图中可以看出在两种载液水平下，波高历时曲线的形式有所不同。低液深液体晃荡自由表面运动比高液深时非线性现象更加明显，高液深共振时，波面出现椭圆余弦波。

3)从图6a)可以看出，当t=0 s时，波面静止；当t=6.04s时，由图6b)中波面右侧壁看出，波面中间凹陷，随着晃荡的剧烈，如图6c)和图6d)所示，波面的三维现象更加明显。图7a)、7b)为Case1、Case2在A和B点处波高历史曲线对比图。可以看出，各曲线的峰值及历时曲线形状具有区别，得出本文采用的模型在晃荡时具有一定三维现象，属有效的三维模型。

3.2 弹性液舱内晃荡液体的动水压强

为了研究装载率对弹性液舱内液体晃荡水动力特性，仍然采用2.1.2的液舱模型，对液舱内液体各观测点进行动力分析，与实验值进行对比，各工况下的动水压强历时曲线见图8～10。

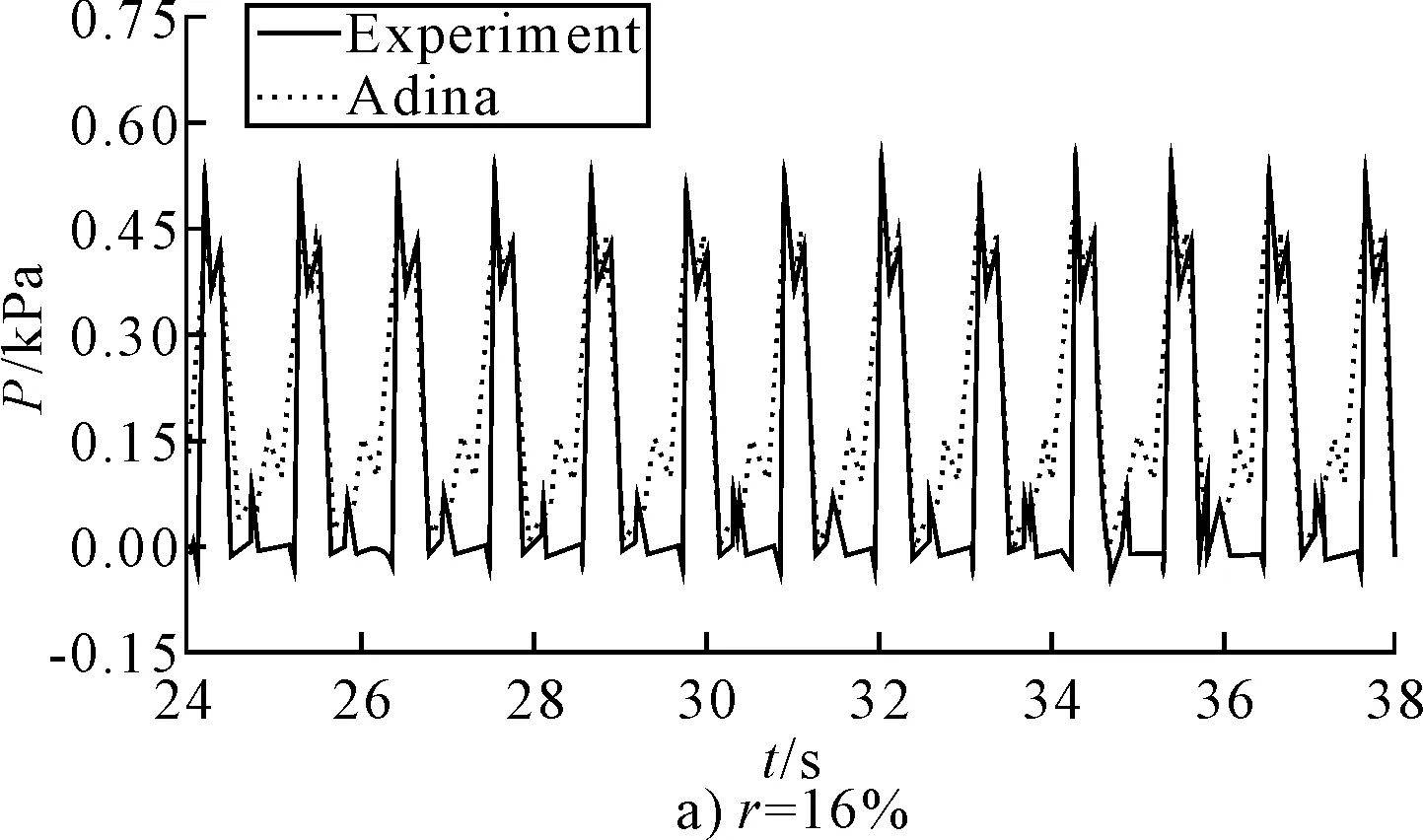
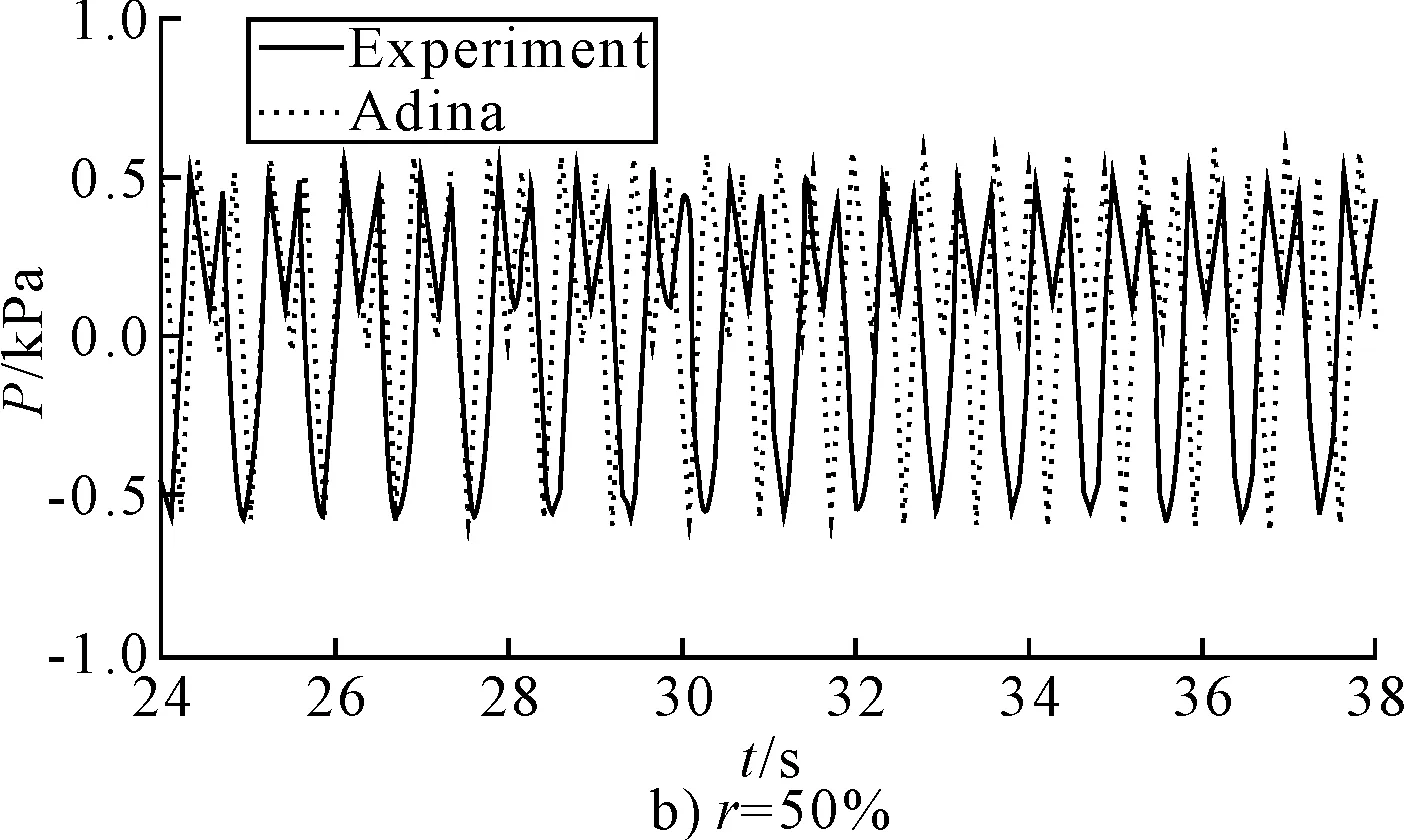
图8 P1点处动水压强历时曲线

图9 P2点处动水压强历时曲线

图10 P3点处动水压强历时曲线

综合分析图8～10，对比不同载液率液舱在共振频率下各观测点动水压强历时曲线可以看出：

1)ADINA模型动水压强模拟结果与实验值基本相符，可见模型验证具有有效性。

2)图8a)为载液率为16%时P1观测点的动水压强历时曲线，图8b)，图9，图10为载液率为50%时P1，P2，P3观测点的动水压强历时曲线，可以看出弹性液舱晃荡动水压强历时曲线出现双峰现象。其中图8a)和图10分别为低液深和高液深时自由表面附近点所受的动水压强，从图中可以明显地看出冲击现象；图8b)和图9为高液深水面以下点P1和P2点的动水压强历时曲线，从图中可以看出压力双峰中前后两峰值相差不大，但后一峰值的持续时间大于前一峰值。且对比图8b)、图9和图10可知，动水压强随液面到底部逐渐减小，这点与理论相符。

由三维波面图可知，液舱侧壁中间部分与同一水平线对应各角点的所受水体冲击有所不同，为了进一步分析了解各角点与对应侧壁面中间部分的动水压强的区别，增加了对侧壁各角点的压力观测点PC1、PC3，其在ADINA中的压强传感器分布见图1，其中PC1、PC3号压力传感器分别与相应的P1和P3号压力传感器处于同一水平位置。对液舱内液体各观测点进行动水压强分析，各工况下的侧壁中点与角点动水压强历时曲线对比见图11～12。

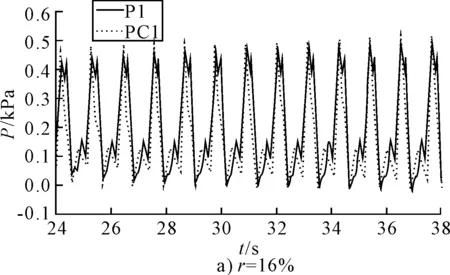
图11 P1,PC1点处动水压强历时曲线

图12 P3,PC3点处动水压强历时曲线

从图11～12可以看出，由于三维现象的存在，各角点的压强值略大于各壁面中点的压强。

4 结论

1)通过与解析解和实验值的比较，基于有限元软件ADINA建立的三维矩形弹性液舱晃荡数值模型是正确及有效的。

2)由于流固耦合作用的影响，当液舱内为低液深时，弹性液舱内液体一阶固有频率大于刚性液舱内液体的一阶固有频率；反之当液舱内为高液深时，弹性液舱内液体一阶固有频率小于刚性液舱内液体的一阶固有频率。

3)两种载液水平下，波高历时曲线的形式有所不同。低液深液体晃荡自由表面运动比高液深时非线性现象更加明显，且自由液面历时曲线出现了双峰。高液深共振时，波面出现椭圆余弦波。

4)三维弹性液舱液体晃荡剧烈冲击舱壁，使得自由表面出现三维效应；另外，动水压强历时曲线出现双峰现象，前后两峰值虽相差不大，但后一峰值的持续时间大于前一峰值，且在同一水平面上各角点的冲击压力略大于舱壁中点，为后续研究提供了参考依据。

本文对三维矩形弹性液舱内液体晃荡的模拟只做了小幅振荡研究，而大幅振荡特别当液面出现翻卷、破碎等复杂情况时液体对舱壁抨击力将会更大，结构稳定性将会更低，将更加具有危害性。在今后的研究中应对大幅振荡进行探讨。

[1] FALTINSEN O M.A numerical nonlinear method of sloshing in tanks with two-dimensional flow[J].Journal of Ship Research,1978(3):193-202.

[2] AKYILDIZ H,UNAL E.Sloshing in a three-dimensional rectangular tank-numerical simulation and experiment validation[J].Ocean Engineering,2006(23):2135-2149.

[3] 朱仁庆.盛液容器内液体二维晃荡的数值模拟[J].华东船舶工业学院学报,1998,12(2):14-12.

[4] GRADINSCAK M.Liquid sloshing in containers with flexibility[D].Australia:Engineering and Science Victoria University Melbourne,2009.

[5] 朱仁庆.液体晃荡及其结构的相互作用[D].无锡：中国船舶科学研究中心,2001.

[6] 张秋艳，任 冰，蒋梅荣.二维矩形弹性液舱内液体晃荡的数值模拟研究[J].船海工程,2012,(4):11-15.

[7] LIU DONGMING,LIN PENGZHI.A numerical study of three-dimensional liquid sloshing in tanks[J].Journal of Computational Physics,2008(227):3921-3939.