浮船坞结构强度直接计算方法对比研究

，

(1.上海船舶设备研究所，上海200031；2.大连海事大学 交通运输装备与海洋工程学院，辽宁 大连 116026)

在有限元结构强度计算时，对于沿直线分布的线载荷可以基于节点等效载荷理论在作用线上施加载荷函数；也可以对载荷函数简单地分段离散进行保守计算。对于处于受力平衡状态的结构计算模型，可以由三点铰支来约束其刚体的平动和转动，也可以应用惯性释放约束。

文中分析了在典型工况作用下的浮坞力学模型，针对其托举载荷沿直线分布、受载后处于平衡态的特点，在通用有限元软件中建立全坞结构强度分析模型，对比分析研究上诉有限元分析方法[1-3]。

1 惯性释放

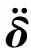
(1)

求解式(1)可得到所有节点为了保持平衡所需的节点加速度，进而可以得到节点惯性力。再将节点的惯性力作为外载荷施加到单元节点上，人为构造出一个平衡力系，这时候计算中不再需要边界条件。这种构造结构静力平衡的方法叫做惯性释放。

2 基于规范的浮船坞结构强度评估

2.1 有限元模型建立

2.1.1 浮坞主要结构说明

计算浮坞为箱型单底整体式钢质浮船坞，该浮船坞主尺度及主要参数见表1。

表1 浮船坞主尺度及主要参数

该坞除坞墙上甲板外，均为横骨架式，肋距为0.55 m，上甲板为纵骨架式，纵骨间距0.50 m，横向强框架不超过4档设置。在坞体内设置3道纵向水密舱壁，横向除设置水密横舱壁外，还在每一压载水舱中设置1道非水密支撑舱壁，以加强横向强度。

2.1.2 模型范围

取整个浮船坞(全坞长、全坞宽、全坞高)范围内的坞体结构主要构件在MSC.patran中建立三维有限元模型，见图1。

图1 全坞三维有限元模型

结构模型中共有461 810个节点、110 131个单元(其中壳单元55 873个、梁单元54 258个)、自由度数为2 770 860个。

2.1.3 计算工况

参照CCS《内河浮船坞技术要求》(2010年)[7]，以工作时的典型工况为计算工况，见图2。即浮船坞的吃水与中龙骨墩高度正好齐平、被载船抬出水面时的状态。

d-计算工况对应的吃水；q1-浮箱甲板水压头；q2-压载水对浮箱甲板压头；q3-压载水对船底板压头；q4-舷外水对船体外板压头；p1-中墩对浮箱甲板压力；G-浮船坞自重。

图2浮船坞典型受示意

计算载荷主要包括：①浮船坞自重；②进坞船的重量；③压载水的重量；④舷外静水压力(不计波浪影响)；⑤剩余压载水的重量；⑥浮箱甲板水头。

上述计算分析中，参照CCS《浮船坞入级规范》(2009年)[8]，将被载船重量假设为矩形加抛物线的分布形式，其中被载船重量的2/3 模拟为矩形、1/3 模拟为抛物线分布。载荷大小为

q1+q2=282.73+212.05×
(1-6.10×10-6×(x-48 400)2)

(2)

在patran中线布函数载荷只能在梁单元上施加，因此针对进坞船的线载荷特点，在进坞船载荷分布的位置建一条刚度趋于零的“软梁”。这样的梁承受载荷后会将载荷传递给该梁所依附的实际结构，在有限元计算过程中由于刚度矩阵中对应“软梁”的刚度趋于零，所以该梁的结构响应也趋于零。但载荷引起的变形趋于无穷，因此这样的梁可以将梁上的载荷很好地传递给所依附的结构，而不会影响结构响应结果的精度，加载后模型见图3。其余静水载荷应用有限元软件中的线性分布面压力函数，以不同的水深为基准施加，加载后模型见图4。

图3 进坞船载荷示意

图4 静水压力载荷示意

2.2 全坞有限元强度评估结果

全坞主要大应力构件有限元直接计算结果与强度评估如表2。

表2 强度评估结果 MPa

全坞应力位移应力分布见图5、6。

图5 全坞变形云图

图6 全坞等效应力云图

3 对比分析

对比分析不同托举载荷施加方式下、不同约束条件下的结构响应结果：即改变规范计算模型的托举载荷施加方式为质量点离散；改变规范计算模型中的约束条件为惯性释放约束，将改变的两个模型分别计算，对计算结果进行对比分析。

3.1 质量点形式施加托举载荷

CCS《浮船坞入级规范》(2009)中规定得到进坞船载荷分布函数见式(2)。

在该软件中指定在有限元模型中进坞船重载荷分布范围为FR18～FR166,施加方式以附加质量单元的形式人为离散给载荷作用线上的节点。质量分布见表3。

表3 进坞船载荷离散

3.2 惯性释放约束施加

在MSC.NASTRAN中，使用support卡片选择节点41940为参考点施加六个自由度的虚约束。惯性释放卡片设置如下。

………………….

PARAM INREL -1

PARAM GRDPNT 41940

SUPORT 41940 123456

…………………

3.3 计算结果对比

用规范计算结果分别对比质量点施加托举载荷和惯性释放约束下的计算结果，见表4。

表4 板单元形心处中面应力分组对比详细结果

表4中计算结果取主要分组中板单元形心中面处相当应力σe的最大值作为对比代表，较为全面的反应了全坞的应力响应。表中的相差意义如下。

通过在“软梁”上加载进坞船载荷使之传递给坞体、节点附加质量单元形式加载进坞船载荷与规范计算的对比看到：质量点计算结果与规范计算结果σemax的相差范围为0.14%～5.45%；惯性释放算结果与规范计算结果σemax的相差范围为-5.64～-0.10 MPa。前种加载方式应力结果大部分小于规范计算结果。其原因是“梁”上的线布载荷会根据等效节点载荷原理，通过Nastran内部算法较为合理地离散到梁的相应节点上；附加质量法根据载荷分布曲线分段离散成阶梯形式加载，在分段时采用保守计算方式增大了进坞船重。因此，梁结果小于质量点结果。偏大的结果依然在工程计算精度范围内反映了船坞的应力响应。

4 结论

1)“软梁”方式对于符合函数规律且线载荷施加部位没有对应的梁单元结构时很适合；对于线或者面载荷不符合函数规律或者全坞、全船模型中载荷平衡调整，质量单元加载方式灵活更加适用。

2)惯性释放要以支座约束为前提，因为惯性释放对模型平衡没有评判，即不平衡力由虚约束点承担，有可能导致计算时的平衡状态不是所需要的，所以是不够准确的。因此，较好的办法是先用支座约束，以支座反力值为平衡调整标准调节模型平衡，然后，再应用惯性释放。这样就可以得到精度较高的结构应力响应。

[1] COOK R, MALKUS D S, PLESHA M E. et al.Consepts and Applications of Finite Element Anslysis[M]. 4 th ed.Wiley&Sons.Inc.2001.

[2] 张少雄，杨永谦.惯性释放在油船结构强度直接计算中的应用[J].船海工程,2004(4):4-6.

[3] 张少雄，杨永谦.船体结构强度直接计算中惯性释放的应用[J].中国舰船研究.2006(1):58-61.

[4] 扶原放，金达锋，乔蔚炜.惯性释放原理在车架结构优化中的应用[J].机械设计与研究.2009(1)：65-70.

[5] 李卫华，黄晓东，郑莎莎，等.有限元法在30万吨级超大型浮船坞设计中的应用[J].船舶设计通讯.2009(6):30-37.

[6] 陈庆强，朱胜昌，姜金辉，等.十七万吨级浮船坞结构有限元强度计算[J].船舶力学，2006(5):100-106.

[7] 中国船级社.内河浮船坞技术要求(2010 年)[S].通函第58 号总第58 号，北京：中国船级社，2010.

[8] 中国船级社.浮船坞入级规范[S].北京：人民交通出版社，2009.