遥感图像椒盐噪声PDE扩散模型*
2013-01-10张洪为
张洪为
(通化师范学院 数学学院,吉林 通化 134002)
椒盐噪声是由感光片不正确曝光产生的,是一种随机的灰度值很小或很大的污染点,在图像中呈现出类似胡椒和盐分的一个个白或黑噪声点[1].遥感图像在获取和传输的过程中会由于椒盐噪声的干扰而使其质量下降,影响了对遥感图像的进一步分析和理解,因此必须对其进行降噪处理.虽然传统的中值滤波法能够有效的去除椒盐噪声,但是中值滤波去除椒盐噪声时有其固有缺点[2],比如说中值滤波并不能很好地保持边缘以及图像中的大量细节信息,所以中值滤波在对边缘和细节要求严格的情况下并不能带来好的处理效果.
偏微分方程去噪方法由于其良好的性能已成为继小波之后另一新型的影像处理工具而受到越来越多研究者的关注[3-5].最具影响力的是perona和malik提出的PM模型[6〗],该模型能根据图像的特征进行不同程度的平滑,将图像的去噪与边缘检测结合起来,具有良好的边缘保持能力.然而随后的研究发现该模型具有“病态”特性[7]和对图像椒盐噪声的无效性[8].随后Alvarez等人针对PM模型的不足提出了改进模型[9],改进后的模型能够有效的克服P-M模型的缺陷,但模型的扩散特性会造成重要的图像信息(如奇异点等)的模糊或丢失[10],而且在图像的边缘保持方面要弱于P-M模型.随后V.Caselles等人提出了不含自由参数测地线活动轮廓(geodesic active contour)模型[11],即GAC模型.令图像的所有水平集按GAC模型运动,得到相应的非线性扩散去噪模型称为自蛇模型[12],实验表明自蛇模型在彻底去除椒盐噪声的同时能够保持大尺度图像的边缘锐度,但容易丢失细小纹理信息,且当图像中椒盐噪声密度较大时,去噪后的图像中容易残留少量噪声点.
本文针对自蛇模型在去除椒盐噪声时具有不彻底性以及容易丢失细小纹理信息,将基于图像边缘、椒盐噪声和平坦区域的引导扩散函数替换自蛇模型中仅依赖于梯度的引导扩散函数,提出一种新的基于椒盐噪声的非线性扩散模型.该模型在有效去除椒盐噪声的同时能够保持图像的边缘和纹理细节信息.实验结果验证了模型的有效性和稳定性.
1 基于水平集运动的扩散模型
针对PM模型难以去除椒盐噪声,Alvarezl等人在文献[11]中令图像的所有水平集做平均曲率运动(MCM),即用图像函数替换平均曲率运动(MCM)方程中的嵌入函数,得如下非线性扩散模型:
(1)
式中该模型中的u0(x,y)为观测图,u(x,y,t)为时间尺度t下u0(x.y)的平滑版本,u和|u|分别为梯度和梯度模值,表示图像所有水平集的曲率,(1)式可进一步化为如下形式(称为方向扩散模型):
(2)
由于方向扩散模型等价于对图像做中值滤波(在结构元素半径趋于零的极限情况),因此方向扩散模型能够很好的去除图像中的椒盐噪声,克服了P-M模型的不足,但该模型中退化的扩散项只沿与梯度正交的方向进行扩散,这样通过该模型平滑后的图像,虽然可以保持图像的线条边缘,但却有可能造成奇异点的模糊,甚至丢失.
1997年,V.Caselles等人在活动轮廓模型的基础上进一步提出了不含自由参数测地线活动轮廓模型,简称GAC模型.该模型的提出是PDE方法在图像分割应用中的重大突破.令图像的所有水平集按GAC模型运动,则可得如下的非线性扩散去噪模型(称为自蛇模型)[12]:
(3)
该模型可进一步展开为:

上式右端第一项称为扩散项,相当于方向扩散模型中引入了边缘引导函数f(|u|),该项可去除图像中的椒盐噪声.第二项称为冲击项,具有增强图像边缘的作用.理论分析与实验结果表明自蛇模型在去除图像中椒盐噪声同时能够保护大尺度对象的边缘锐度,但当椒盐噪声密度较大时,该模型会存在去噪不彻底的现象.这是因为模型中的引导扩散函数是仅依赖于梯度的,认为梯度大的地方是图像的边缘,在梯度大的地方进行弱扩散保护图像的边缘,然而梯度大的地方也可能是椒盐噪声.
2 椒盐噪声扩散模型
2.1 基于图像的边缘点、椒盐噪声点和内部点的引导扩散函数
为了去除图像中的脉冲噪声,文献[13]定义了一种识别图像中的边缘点、椒盐噪声点以及内部点的因子ENI,具体过程如下:
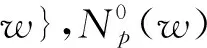
d(p,q)=|u(p)-u(q)|
(4)
(5)
最后将像素点p的ENI定义为
(6)
1)对于椒盐等脉冲噪声的ENI是最小的,接近于零,因为椒盐噪声的灰度强度与其周围像素的灰度强度相比是比较突出(很大或很小)的.
2)对于图像边缘上的像素点ENI大小处于中间水平,接近于N/2.
3)对于图像内部像素点ENI是最大的,接近于N.
为了能在图像的椒盐噪声点和内部点进行强扩散,而在图像的边缘点进行弱扩散,将扩散函数定义为

(7)
2.2 新模型的建立
针对自蛇模型在去除像椒盐噪声时具有不彻底性以及容易丢失细小纹理信息,本文将扩散引导函数g(ENIp(u,w,T'))代替自蛇模型中的引导函数f(|u|),得如下的非线性扩散模型:
(8)
式中,u0(x,y)为观测图,u(x,y,t)为时间尺度t下u0(x,y)的平滑版本,u和u|分别为梯度和梯度模值,g(ENIp(u,w,T'))为引导扩散函数.
分析 当P点是图像的边缘点时,ENIp(u,w,T)值接近于N/2,而g(ENIp(u,w,T))接近于0,此时进行弱扩散保护图像的边缘.当P点是图像的椒盐噪声点或图像的平坦区域点时,ENIp(u,w,T)接近于0或N,而g(ENIp(u,w,T))接近于1,此时进行强扩散以快速的去除噪声.因此该模型具有去除椒盐噪声和保护图像边缘的双重功能.
2.3 提出模型的离散化
设时间步长Δt,空间变量x与y的步长均为1,利用有限差分方法,采用如下的“半点离散化”方案,由
可得
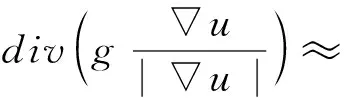
式中的每一项,可用u和g在整点的值作近似表达.现以第一项为例,有
(u)
所以

式中

g在半点的值则可用相邻两“整点”的平均值近似为
对其他三项作类似的处理,便得
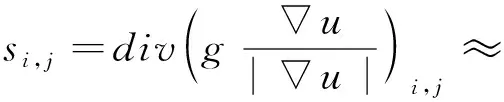
(9)
上述模型算法实现的具体步骤如下:
Step1 初始化:选取大小为M1×N1的含噪图像un,并记u0=un,收敛精度为μ.选择合适的邻域参数w和阀值T'.
Step2 循环计算n=0,执行如下过程:

Step2.2 然后通过式(7)计算相应的扩散函数,即

Step2.3 按照式(8)计算n+1时刻的图像un+1

Step2.4 若|un+1-un|>μ,置n=n+1,转向Step3,否则,返回执行Step2.1.
Step3结束.
3 实验与讨论
为了验证本文方法的有效性,选取了大小为256×256的两幅遥感图像作为测试图像,在多种强度的椒盐噪声下,将所提出的模型与方向扩散模型和本文模型进行了比较.客观评价指标采用如下定义的峰值信噪比(PSNR)
式中:u*(i,j)是算法去噪后的图像;u0(i,j)是标准的不含噪声图像;m和n分别是图像的长和宽.
图1~2是利MATLAB分别对遥感图像A和B添加不同密度的椒盐噪声利用方向扩散模型、自蛇模型和本文模型去噪后的效果图.

图1 三种方法对包含不同密度椒盐噪声A图像的去噪效果比较

图2 三种方法对包含不同密度椒盐噪声B图像的去噪效果比较
从图1~2可以看出,方向扩散模型虽然能够比较彻底的去除椒盐噪声,但却造成了纹理细节的过分丢失,自蛇模型在去除噪声的同时能够保持图像的边缘,但当图像中椒盐噪声密度较大时,发现去噪后的图像中会残留少量的噪声,而采用本文模型去噪后的图像不仅能彻底的去除椒盐噪声,而且能够保持图像的边缘和纹理细节信息.
为了从客观上进一步评价三种模型的去噪性能,对以上去噪结果进行峰值信噪比统计,得曲线图3(a~b).从中可以看到对于不同的遥感测试图像和不同密度的椒盐噪声,本文模型去噪后的图像与方向扩散模型和自蛇模型相比具有更高的峰值信噪比.

图3 三种模型去噪的PSNR曲线图比较
4 结论
本文针对自蛇模型去除遥感图像椒盐噪声的不彻底性以及容易丢失纹理细节的不足,将一种能够依赖于图像边缘点、椒盐噪声点和内部点进行扩散的引导函数引入到自蛇模型中,提出了一种能够有效去除椒盐噪声的PDE扩散模型.该模型能够在彻底去除椒盐噪声的同时保持图像的边缘和纹理细节信息.实验结果验证了所提模型的有效性和稳定性.
参考文献:
[1]王相海,张洪为,李放.遥感图像高斯与椒盐噪声的PDE混合去噪模型研究[J].测绘学报,2010,39(3):283-294.
[2]阮正旺,张建州,张亮.清除椒盐噪声点的局部L1去噪保边方法[J].中国图像图形学报,2010,15(6):867-872.
[3]钱惟贤,陈钱,顾国华,等.一种新型图像噪声抑制各向异形扩散算法[J].中国图像图形学报,2009,14(4):666-680.
[4]Zeng Weili,Tan Xianghua,Lu Xiaobo.Domain-based noise removal method using fourth-order partial differential equation[J].Journal of Southease University(English Edition),2011,27(2):154-158.
[5]Sun Xiaoli,Li Min,Zhang weiqiang.An improved image denoising model base on the directed diffusion equation[J].Computers and Mathematics with Applications,2011,61(8):2177-2181.
[6]Perona P, Malik J.Scale-space and edge detection using anisotropic diffusion[J].IEEE Trans.on Pattern Anal Machine Intell,1990,12(7):629-639.
[7]Catte F,Lion P L,Morel J M,Coll T..Image Selective Smoothing and Edge Detection by Nonlinear Diffusion[J].SIAM Journal on Numerical Analysis,1992,29:182-193.
[8]祝轩,周明全,朱春香,等.曲率驱动与边缘停止相结合的非线性扩散及其在图像去噪中的应用[J].光子学报,2008,37(3):609-612.
[9]Alvarezl,Lions P L, Morel J M.Image selective smoothing and edge detection by nonlinear diffusion II[J].SIAM J Num Anal,1992,29(3):182-193.
[10]王相海,张洪为,王爽.一种小波变换模极大值的扩散模型[J].中国图像图形学报,2011,16(6):1080-1085.
[11]Caselles V,Morel J M,Sapiro G.Geodesic active contours[J].Int J.Comput.Vision,1997,22:61-79.
[12]王大凯,侯榆青,彭进业.图像处理的偏微分方程方法[M].北京:科学出版社,2008.
[13]Jian Wu and Chen Tang.PDE-Based Random-Valued Impulse Noise Removal Based on New Class of Controlling Functions[J].IEEE Trans on Image Processing.2011,PP(99):1-10.
