FS4132结构磁空间群的不可约共表示
2013-01-10申香花
申香花
(通化师范学院 物理学院,吉林 通化 134002)
群论是揭示物理体系的对称性所蕴藏的深层含义的数学工具,群表示在群论知识体系中占有重要地位.在群论中引入磁空间群可以更加准确地对物理结构进行描述,更能揭示量子系统的对称性.磁空间群中含有反幺正元素,所以不适用寻常空间群的表示,而应该用共表示理论.由于磁空间群的复杂性和计算方法的限制,对磁空间群不可约共表示的计算还很不完整,本文应用诱导共表示的方法,计算了第四类磁空间群FS4132的不可约共表示.
1 诱导磁空间群不可约共表示的途径


(1)
其中P(k)为Hk的小旁群,定义为:
P(k)={α:αk=k+Kq,∀{α|t}∈G}

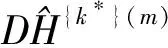
首先把磁空间群对应的空间群H按Hk作如下分解:
(2)
根据波矢群Hk与磁小群Mk的关系,M按子群Mk旁集分解有如下关系.
若

(3)
若
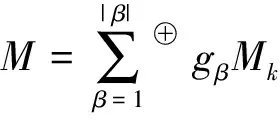
(4)
对(3)式情况,当∀g∈H时,由Mk的不可约共表示诱导M的不可约共表示有:
(5)
其它(α≥|β|+1,β≤|β|或α≤|β|,β≥|β|+1)的非对角超矩阵元均为零.
当∀g∈AH时,由Mk的不可约共表示诱导M的不可约共表示有
(6)

2 FS4132磁空间群的结构
3 计算结果
本文对FS4132磁空间群第一布里渊区X、L点的共表示进行了计算,由于篇幅所限,下面只给出了部分元素的不可约表示:
参考文献:
[1]陶瑞宝.物理学中的群论[M].高等教育出版社,2000.
[2]陈金全.群表示论的新途径[M].上海:上海科学技术出版社,1984.
[4]C.J.Bradley and A.P.Cracknell:The Mathematical Theory of Symmetry in Solid——Representation Theory for Point Groups and Space Groups[M].London:Oxford University Press,1972.
