Clifford群的若干性质及应用*

宋元凤,李武明，孙业进

(通化师范学院 数学学院,吉林 通化 134002)

1 预备知识

Clifford代数Clp,q的Clifford群Γp,q由Lipschitz于1880年代定义为

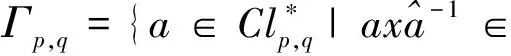
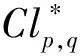
1.1 Clifford代数Clp,q及其生成空间p,q

并由此确定Clp,q的一组基:

1,e1,e2,…,ep+q
e1e2,e1e3,…,e1ep+q,e2e3,…,e2ep+q,…,ep+q-1ep+q
……
e1e2…ep+q.

在如上基元中，称es1,s2…sk(=es1es2…esk)为Clp,q的k次单位向量.特别地，1称为Clp,q的零次单位向量.

1.2 在Clp,q的三种对合

在Clp,q中任取元素

a=a0+a1e1+…+ap+qep+q+…+a12e12+…+e(p+q-1)(p+q)e(p+q-1)(p+q)+…+a12…(p+q)e12…(p+q),a可简记为

，

其中〈a〉k(k=0,1,…,p+q)称为a的k次向量部分.由此定义

其中τ(k…21)为排列k…21的逆序数,依次称为a的分次对合,a的反演,a的Clifford共轭.

2 Clifford群的等价命题

本节将给出在一定限制条件下的(1)式的等价定义.

证明 设

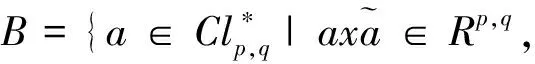
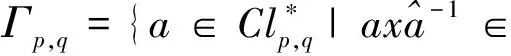
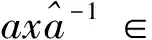
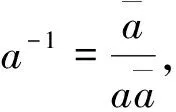
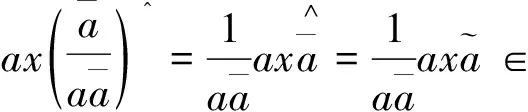
因此a∈B,即Γp,q⊆B.

Γp,q=

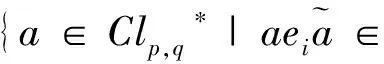
(3)

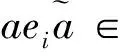
由引理1、引理2可得下面定理.

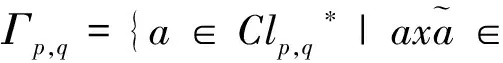
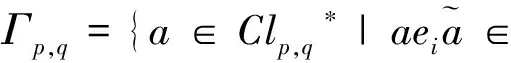
(4)

例1 任取a=a0+a1e1+a2e2+a3e3+a4e12+a5e13+a6e23+a7e123∈Cl0,3,有

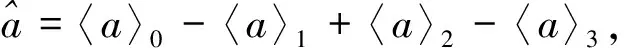
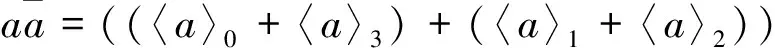
注意到〈a〉0+〈a〉3∈Cen(Cl0,3),可得

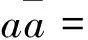
上例表明,定理1的等式不适用于所有的Clifford代数Clp,q,但一定适用于某些Clifford代数Clp,q.下面我们将以实例说明定理1用于考察实际问题的有效性.

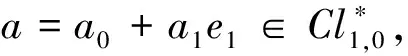
由定理1知,a∈Γ1,0⟺a0a1=0.

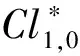
Clifford代数Clp,q的Clifford群Γp,q在数学与物理中有广泛的应用,pin(p,q)群与SPin(p,q)群均为Γp,q的子群.本文给出当Clp,q中元素与其共轭之积为实数时Γp,q的三种等价定义方式,寻找限制条件较弱的等价定义方式是尚待研究的问题.

参考文献：

[1]P.Lounesto.Clifford Algebras and Spinors[M].New York:Cambridge University Press,1997.

[2]Jean Gallier.Clifford Algebras,Clifford Groups and a Generalization of the Quaternions: the Pin and Spin Groups[M].Philadelphia: Department of Computer and Information Science Technical Reports,2007.

[3]Yu Xuegang,Zhang Shuna,Huang qiunan.Clifford Algebraic Spinor and the Dirac Wave Equations[J].Advances in Applied Clifford Algebra,2001,11(1):27-38.

[4]贺福利,杜金元.泛欧式空间的Clifford群、扭群、旋群及它们的李代数[J].数学杂志,2011,31(3):519-524.

[5]宋元凤,李武明,丁宝霞.Clifford代数CLp,q的中心子代数[J].通化师范学院学报,2011,32(12):4-5.