结合look-ahead值排序的自适应分支求解算法

王海燕，欧阳丹彤，张永刚，张良

（1.吉林大学 计算机科学与技术学院，吉林 长春 130012；2.吉林大学 符号计算与知识工程教育部重点实验室，吉林 长春 130012；3.吉林师范大学 计算机学院，吉林 四平 136000）

1 引言

约束满足问题(CSP, constraint satisfaction problems)是人工智能领域研究的热点问题。而 CSP的经典求解方法是将回溯搜索与约束传播相结合。搜索过程是基于某种分支策略，并由变量和值排序启发式引导。当前，在CSP的回溯搜索中，搜索的分支选择有多种策略，其中2-way和d-way[1]是2种最标准的分支策略。在2-way分支策略下，在选择了变量x和x域中的某个值ai后，建立2个分支，一个分支是将x=ai加入到问题中进行传播，另一个分支是将x<>ai加入到问题中进行传播。在2个分支都失败时，算法回溯。在传播x<>ai时，可以选择不同于x的变量y的某个值继续传播，也可以选择变量x的不同于ai的其他值进行传播。如果将问题限定为后一种情况，则称其为受限的 2-way分支[2]。而在d-way分支策略下，变量x被选择之后，建立d（d>2）个分支，每个分支对应x的一个值分配。在第一个分支中，x分配值a1，并引发约束传播，如果这个分支失败了，则从x论域中移去a1，然后给x分配a2，以此类推，即，在x=ai失败后，算法必须选择x的下一个可用值。如果d个分支都失败，算法回溯。受限的2-way在某种程度上近似于d-way分支。

Kostas通过实验证实[2]，不同的变量排序启发式对2-way分支策略和d-way分支策略的影响是不同的。当从简单的变量排序启发式dom[3]一直测试到更经典的启发式如dom/ddeg[4]时，2-way分支策略要优于d-way分支策略。但采用当前公认最好的dom/wdeg[4]变量排序启发式时，d-way分支却比2-way分支更有效。而且实验结果表明，受限的2-way分支策略与d-way分支策略效果很接近。基于不同分支策略的不同表现，Kostas提出2个启发式，在搜索中的某些点应用它们，根据启发式的决定在完全的2-way分支和受限的2-way之间进行选择。从根本上实现自适应分支选择。

本文首先在dom/wdeg变量启发式下，对受限的2-way分支和完全的2-way分支策略进行了详细的对比实验。结果表明，在不同实例上，受限的2-way和完全2-way表现出不同的性能。然后，将4种自适应分支方法与上面2种分支方法在标准测试库 Benchmark中的 composed、bqwh、domino、graph进行了求解效率的对比，实验结果充分展示了自适应分支策略的优势。同时，由于相关研究中没有充分考虑值启发式对自适应分支策略的影响，而 look-ahead[5]值启发式能够有效引导搜索到更可能成功的分支。为进一步提高算法效率，将自适应分支策略与look-ahead两者结合起来，提出一种新算法AdaptBranchLVO，该算法在自适应分支的基础上加入look-ahead值启发式，在有效避免误用不合适分支策略的基础上，考虑到每个值对未来情况的影响，选择最有可能成为解一部分的值优先实例化，以更快求出最终解。在sat和unsat两大类问题的多个标准类实例上进行实验，结果表明，新提出算法在效率上明显优于已有的自适应分支方法，即加入look-ahead值启发式的自适应分支求解效率有更大幅度的提高。

2 背景知识

一个CSP表示为一个三元组（X,D,C），其中，X={x1,…,xn}，是一组n个变量的集合；D={D(x1) ,…,D(xn)}是对应于每个变量的一组论域；C={c1,…,ce}是e个约束的集合。每个约束c表示为有序对（var(c),rel(c)），其中，var(c)={x1,…,xk}是X的一个有序子集，而 rel(c)是D(x1)×…×D(xk)的子集[7]。验证一个元组是否满足约束c的过程称为一次约束检查。

回溯搜索与约束传播的结合方法是求解 CSP的经典方法。搜索过程是基于某种分支策略，并由变量和值排序启发式引导。

在经典的变量排序启发式（VOH, variable ordering heuristic）中，dom/wdeg以其普适性及高效性受到研究者的广泛重视。它是基于fail-first原则，为每个约束分配一个权值，初始设置为 1。每次约束引发一个冲突（例如一次 DWO），它的权值就加 1。每个变量都与一个加权度相关，它是包含此变量和至少一个未实例化变量的所有约束的权的总和。Dom是现有论域的大小，dom/wdeg启发式选择现有域大小与带权的度比值最小的变量。在后文中，都默认使用dom/wdeg变量排序启发式。

值实例化的顺序对约束求解效率有着深刻的影响。而搜索中向前看（look-ahead）是提高求解效率的关键技术，它能在搜索中尽早导致失败节点产生，从而为变量排序提供有价值信息。当前，look-ahead技术已成功用于值排序启发式，特别是针对难解CSP。典型look-ahead值排序(LVO, lookahead value ordering)启发式[5]有：最小冲突(MC,min-conflicts)启发式，最大论域(MD, max-domainsize)启发式，加权最大论域(WMD, weighted-maxdomain-size)启发式和论域大小分值(PDS, point-domain-size)启发式等4种。其中，MC是针对当前变量论域中每个值，考虑与当前变量相关的未实例化变量的论域中与这个值不相容值的个数，并按此个数的升序对当前变量的值排序。即总是优先选择冲突值最少的值；MD是针对当前变量论域中每个值，考虑所有与当前变量相关的未实例化变量移去不相容值的剩余子论域，优先选择在未实例化变量中产生最大的最小剩余子论域的值；WMD是MD的一个改进版本，目的是解决第3种启发式中，当前变量论域中可能有几个值产生相同大小的剩余子域集合而导致“结”的产生的问题。WMD优先选择剩下更大子论域的值，这点和MD相似，只是打破“结”的方法不同。它是根据具有给定剩余子论域大小的未实例化变量的数目来打破“结”的；PDS给当前变量论域中每个值打分。依据是所有与当前变量相关的未实例化变量移去不相容值的剩余子论域。每个大小为1的子论域给8分，每个大小为2的子论域给4分，每个大小为3的子论域给2 分，每个大小为4的子论域给1分。优先选择具有最小总分的值。已有实验表明[5]，MC启发式是LVO启发式中效果最好的，所以选择它进一步实验。后文中提到的LVO均指MC。

3 分支策略性能对比

2-way和d-way[1]这2种标准的分支策略在不同实例上的表现不同。时而2-way分支策略胜出，时而受限的2-way分支策略胜出，时而两者持平。研究者考虑在搜索的不同位置选择更合适的分支策略，即自适应分支策略。实现的基本思想是根据具体问题的结构将不同分支组合到一起，借助于启发式和传播函数，达到压缩搜索空间的目的，进而提高求解效率。代表工作为2010年Kostas提出的自适应分支策略[2]，其中提到2种启发式策略：Hsdiff(e)和Hcadv(VOH2)。前者是基于变量排序启发式分值差异的自适应分支启发式，其工作原理是：假如当前变量是x，且VOH建议去选择一个其他变量y，当|score(y)-score(x)|>e时，接受这个建议。其中，score(x)和score(y)是VOH分配给变量x和y的值，而e是一个可变的阈值参数。后者为辅助顾问启发式中，其主要思想为：假如当前变量是x，且算法用到的VOH（VOH1）建议去选择另一个变量y，仅当辅助VOH（VOH2）也选择y时，接受这个建议，即当scoreVOH2(y)>scoreVOH2(x)时，其中，scoreVOH2(x)和scoreVOH2(y)是VOH2[8]分配给变量x和y的值。受文献[2]中实验结果启发，在Hsdiff(e)中，VOH采用dom/wdeg，e取值0.1；Hcadv(VOH2)中辅助启发式为wdeg。2个启发式可合取或析取应用。

本文在文献[2]基础上进行实验，选取不同的Benchmark测试问题类，以进一步验证自适应分支策略的优势。在实验中将Hsdiff(0.1)和Hcadv(wdeg)简记为H1和H2，它们的合取和析取记为H12∧和CPU运行时间实验结果如表1所示。表中每个实例 CPU运行时间的最好情况都用黑体显示。从表中可以看出，自适应分支策略总是趋于选择效果好的分支方式，有些情况甚至比两者中的优胜者更好。

4 AdaptBranchLVO算法

为进一步提高约束求解效率，本文在自适应分支的基础上加入look-ahead值启发式。考虑到求解难解CSP时，多数时间花费在探查搜索空间不可能产生问题解的分支上。为减少回溯，应首先尝试那些更可能导致相容解的值。即使被选择的值是某个解的一部分可能性的微小增大都能对找到解的时间开销有着本质上的影响。本文利用在自适应约束传播look-ahead阶段中收集到的信息改进值排序启发式。在自适应分支框架上，加入文献[5]中的LVO启发式，它根据look-ahead得到的信息为当前论域中的值划分等级。当前变量则用最高级别的值实例化。得到的算法是AdaptBranchLVO，其维持弧相容的框架描述如图1所示。

由于需要区分完全的 2-way策略和受限的2-way策略，而这2种策略的区别仅在于下一个实例化的变量改变与否。所以用布尔变量Restricted_or_Not（第2行）作为是否需要判断限定分支的标识变量，其值为真，表示下一次需要判断是否限定分支，反之不需要。Free_variables（第4行）是未实例化的变量。Soulution_Stack（第 5行）为存储解的动态堆栈。AdaptBranchLVO算法的 MAC过程为，只要还有未实例化的变量，就根据 SELECT_VAR函数（下面详述）选择出一个变量（第7行），并按LVO为其选择一个值（第9行）。自适应分支的具体实现在SELECT_VAR函数中，总体上实现了自适应分支和LVO结合的方式。

表1 自适应分支策略与标准分支策略的比较（单位：ms）

图1 MAC框架描述

SELECT_VAR函数在整个MAC的过程中尤为重要（如图2所示）。在选择变量的时候，主要考虑的是Restricted_or_Not的值。在其值为真的前提下，需要判定是否限定分支，判定的依据是H1和H22种自适应分支启发式的满足情况，并根据判定结果选择合适的变量作为下一个实例化对象。Switch的4个分支（第17）～25)行）对应着4种启发式运用的方式。如果使用 dom/wdeg启发式筛选出变量恰为当前变量cur_var，则不执行启发式H1、H2。

图2 选择变量过程

5 实验结果

为验证AdaptBranchLVO算法优势，本文利用标准测试库Benchmark中的多类问题实例对算法进行测试。实验是在AMD Athlon(tm) 64 X2双核处理器3600的DELL计算机上完成的，主频为1.90 GHz，内存为1.00 GB，操作系统为Microsoft Windows XP Professional。测试环境为 Microsoft Visual Studio 2008。将AdaptBranchLVO和已有自适应分支算法进行比较，考查 CPU运行时间、约束检查次数和搜索树生成节点数3项技术指标。CPU时间（单位：ms）记为cpu，约束检查次数记为#ccks，搜索树生成节点数记为#nodes。将AdaptBranchLVO算法应用于搜索中，得到与原自适应分支算法的实验对比结果，如表2所示，最好的情况均用黑体标记。实验结果表明：新提出算法在时间开销、约束检查次数及搜索树生成节点数方面均明显优于已有自适应分支算法。

为检验新提出算法的高效性及普适性，本文在可满足问题（简记为sat）和不可满足问题（简记为unsat）两大类问题上进行实验，共选取composed、bqwh、driver、frb、rlfap、geom、ehi、QCP 等 8 类问题，并从每个分类中选出5～10个实例进行测试，取时间测试结果的平均值作为此分类实例的实验数据。

在sat类中，选出部分测试结果如表3所示。很清楚看出，加入 LVO的自适应分支策略在平均时间上明显优于未加入的情况，尤其在 composed-25-10-20和geom两类问题上，总体效率提高了2倍左右。有些更是提高了3倍左右，如frb30-15在H1上的改进。总之，AdaptBranchLVO综合性能明显优于已有自适应分支算法。

在unsat问题类上，本文给出composed-25-1-2、ehi-85、QCP-10和rlfapModScens 4类子问题的测试结果如表 4所示。可以看出，在不可满足问题类上，加入LVO的自适应分支求解效率整体上也优于已有自适应分支算法。需要指出的是，对于rlfapModScens问题实例，加入LVO策略的基于H2和H12˄自适应分支求解算法在平均性能上比已有自适应分支约束算法差，考虑这和rlfapModScens问题实例的特殊结构有关，未来工作将深入探讨和问题结构密切相关的自适应约束求解算法。

表2 AdaptBranchLVO与已有自适应分支算法对比结果

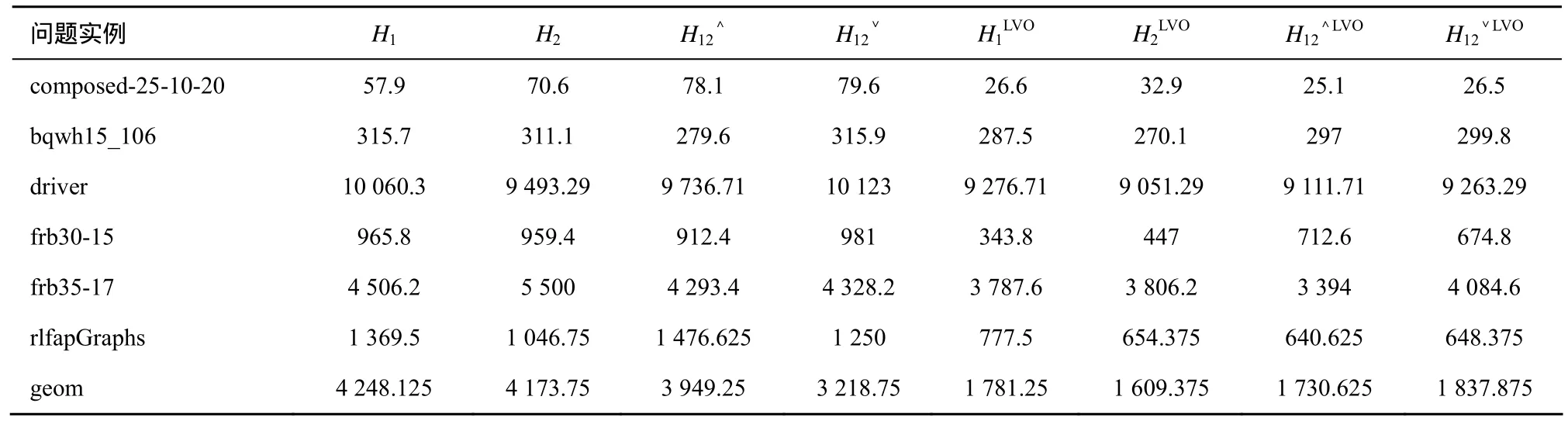
表3 sat类上平均求解时间对比（单位：ms）

表4 unsat类上平均求解时间对比（单位：ms）

6 结束语

不同分支策略在不同实例上有不同效率表现。自适应分支策略以选择最合适分支为最终目标，是自适应约束求解方法的重要研究方向。分支策略性能对比实验充分证明：引入自适应分支可以有效提高约束求解效率。本文基于新近提出的自适应分支约束求解框架，结合look-ahead值启发式，提出一种新的约束求解算法AdaptBranchLVO。并针对标准测试库Benchmark中的典型sat和unsat问题进行比较实验。实验结果表明，加入look-ahead值启发式的自适应分支约束求解方法能更有效地提高约束求解的效率。未来工作考虑将学习型值启发式嵌入到自适应分支框架中，以进一步提高约束求解效率。

[1] BALAFOUTIS T, PAPARRIZOU A, STERGIOU K.Experimental evaluation of branching schemes for the CSP[A].CoRR[C].2010.

[2] BALAFOUTIS T, STERGIOU S.Adaptive branching for constraint satisfaction problems[A].Proceedings of ECAI[C].Lisbon, Portugal,2010.855-860.

[3] HARALICK R M, ELLIOTT G L.Increasing tree search efficiency for constraint satisfaction problems[J].Artificial Intelligence, 1980,14(3)： 263-313.

[4] BOUSSEMART F, HEREMY F, LECOUTRE C,et al.Boosting systematic search by weighting constraints[A].Proceedings of ECAI[C].Valencia, Spain, 2004.482-486.

[5] DANIEL FROST, RINA DECHTER.look-ahead value ordering for constraint satisfaction problems[A].Proceedings of IJCAI [C].Montréal, Québec, Canada, 1995.572-578.

[6] LIKITVIVATANAVONG C, ZHANG Y L, BOWEN J,et al.Arc consistency during search[A].Proceedings of IJCAI[C].Hyderabad,India, 2007.137-142.

[7] STAMATATOS E, STERGIOU K.Learning how to propagate using random probing[A].Proceedings of CPAIOR[C].Pittsburgh, USA,2009.263-278.

[8] GRIMES D, WALLACE R J.Sampling strategies and variable selection in weighted degree heuristics[A].Proceedings of CP[C].Providence, USA, 2007.831-838.