非扩张映射族和单调映射迭代算法的收敛性

史沧红, 吴定平

(成都信息工程学院数学学院,四川成都610225)

0 引言

设H是实Hilbert空间,C是H的非空闭凸子集,映射 T:C→C,用记映射的不动点集合,如果满足:

则称为非扩张映射。

设H是一Hilbert空间,且 C是H的非空闭凸子集,且设 A:C→H是一映射,经典的变分不等式定义为IV(A,C),即找到 x*∈C使得:

变分不等式IV(A,C),的解集定义为Ω。A:C→H称为α-逆-强单调映射[1-2]如果存在正实数α使得:

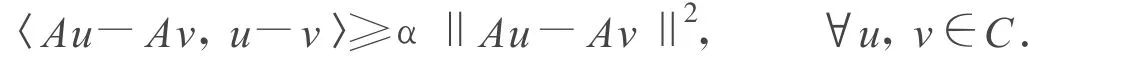
Yonghong Yao,Jen-Chih Yao[3]引入了一种迭代算法,通过这种迭代找到了实Hilbert空间一个非扩张映射不动点集和α-逆-强单调映射变分不等式解集的一公共元,从而建立了强收敛定理。

Tomoo Shimizu,Wataru Takahashi[4]引入了Hilbert空间中非扩张映射族的一种迭代算法,证明了这个迭代强收敛于非扩张映射族的公共不动点;首先,他们考虑了有限交换非扩张映射族的迭代算法,并且证明了这个迭代强收敛到这族映射的公共不动点;进而,他们考虑到了非扩张映射半群的迭代算法,并且这个迭代序列强收敛于非扩张映射半群的一公共不动点。

文中,基于文 Yonghong Yao,Jen-Chih Yao和Tomoo Shimizu,Wataru Takahashi,提出两种新的迭代算法(7),(17),证明了其强收敛性,改进和推广了文献[3-10]等人的相应结果。

1 预备知识

设H是一实Hilbert空间,且 C是H的一非空闭凸子集,对每 x∈H,在C中存在唯一的最近点,定义为PCx,满足:

PC:H→C称为度量投射。易见

(1)PC:H→C是非扩张映射且满足:

(2)对每个 x,y∈H,PCx∈C有下面的性质:

(3)对∀x∈H,y∈C,∃u∈C,满足:

引理1[11]设E是一内积空间,那么对所有的 x,y,z∈E和有:

‖α x+βy+γ z‖=α‖x‖2+β ‖y‖2+γ‖z‖2-α β ‖x-y‖2-α γ‖x-z‖2-βγ‖y-z‖2.

引理2[12]设是Banach空间中的有界序列，1,假设对所有的且那么limn→∞‖yn-xn‖=0。

引理3[13]设是一非负实数序列满足:

那么limn→∞an=0。

2 主要结论

定理1 设C是实Hilbert空间H的闭凸子集,设 A:C→H是一α-逆-强单调映射,设S,T:C→C是两个非扩张映射满足ST=TS且F非空,假设由下列迭代给出:

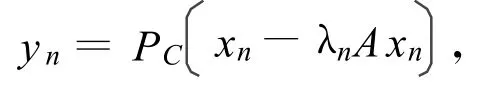
(ⅰ)αn+βn+γn=1,

(ⅱ)limn→∞αn=0,∑∞n=1αn=∞,

(ⅲ)0＜lim infn→∞βn≤lim supn→∞βn＜1,

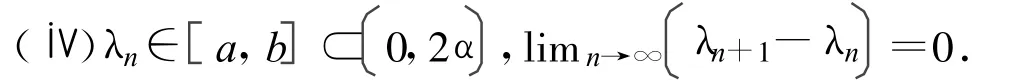
证明 ∀x,y∈C,n≥1,有

因此I-λnA是非扩张映射。设那么

而且

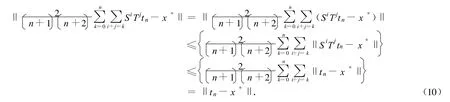
从而

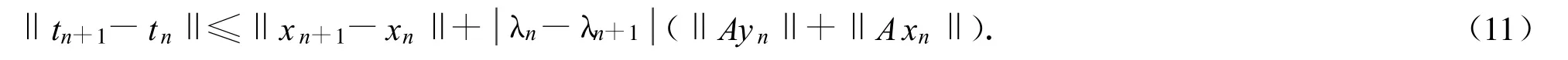
合并式(11)和式(12),有

再从(ⅱ)和(ⅳ),有

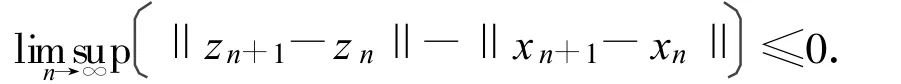
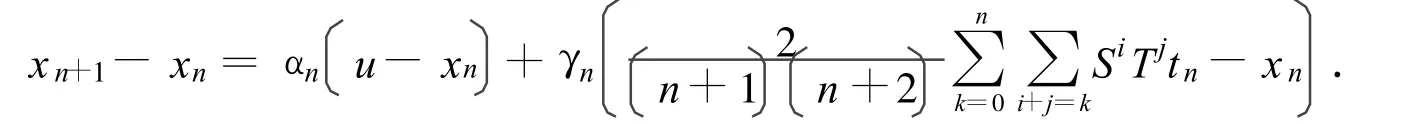
因此

因为 αn→0和从式(14),有

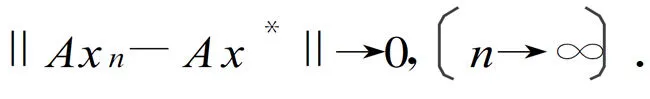
从式(3),有

所以

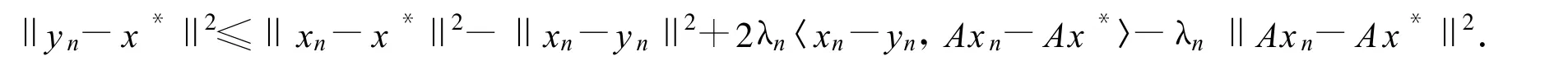
因此

从而

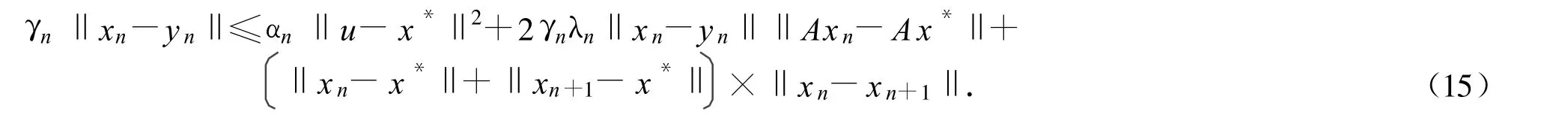
因为 αn→0和且从式(15),有‖xn-yn‖→因为

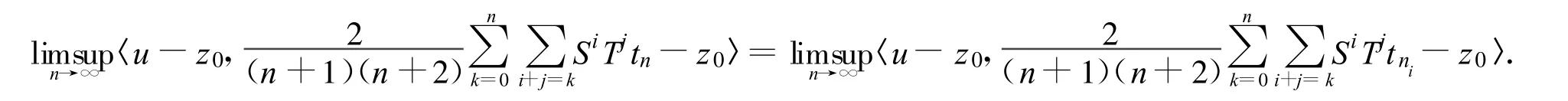
由式(4),有

因此

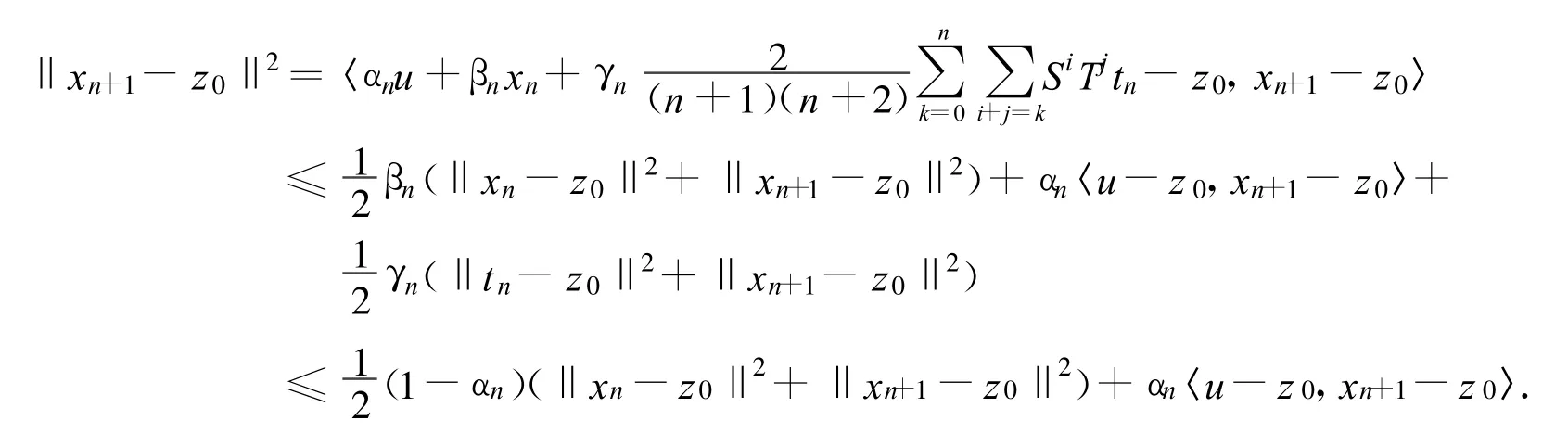
从而

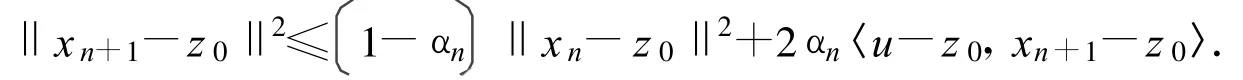
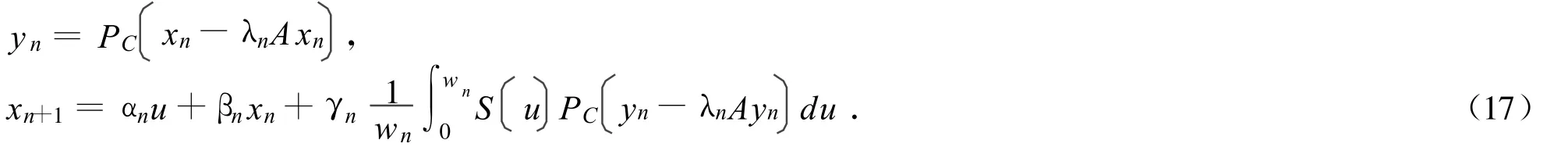
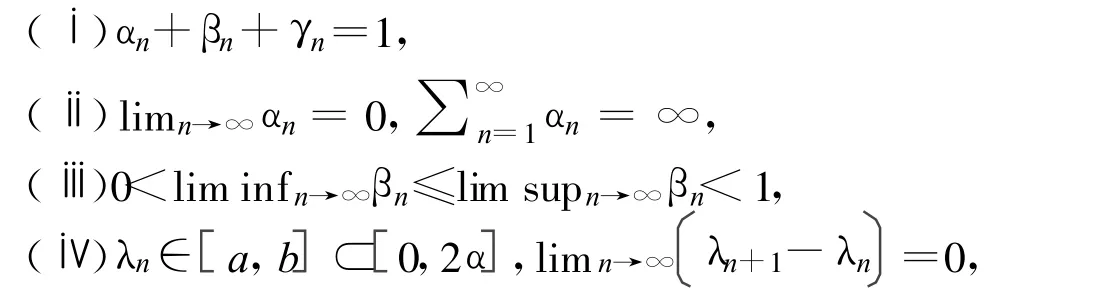
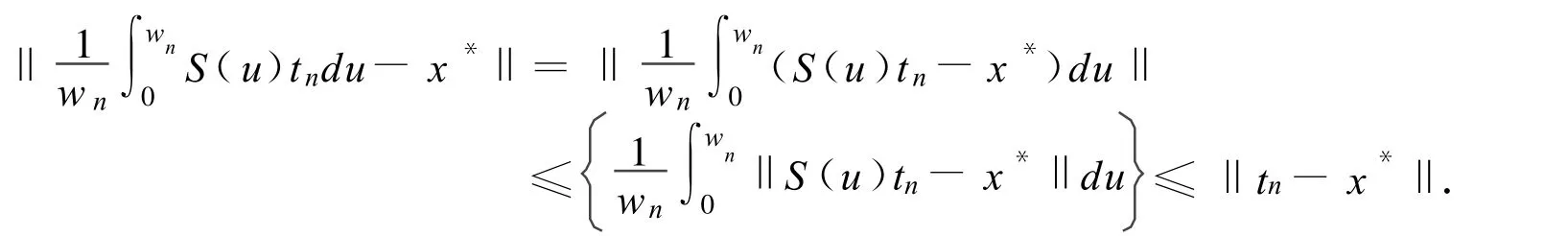
由此可见,定理1和定理2的结论改进和推广了文献[3-4]等的相应结果。

致谢:感谢成都信息工程学院科研项目(KYTZ201004)对本文的资助

[1] F E Browder,W V Petryshyn.Construction of fixed points of nonlinear mappings in Hilbert space[J].Journal of Mathematical Analysis and Applications,1967,20:1977-228.

[2] F Lm,M Z Nashed.Regularization of nonlinear Ill-posed variational inequalities and convergence rates[J].Set-Valued Analysis,1998,6:313-344.

[3] Yonghong Yao,Jen-Chih Yao.On modified iterative method nonexpansive mappings and monotone mappings[J].Applied Mathematics and Computation,2007,186:1551-1558.

[4] Tomoo Shimizu,Wataru Takahashi.Strong Convergence to Common Fixed points of Families of Nonexpansive Mappings[J].Journal of Mathematical Analysis and Applications,1997,211:71-83.

[5] Dingping Wu.Weak Convergence of Ishikawa Iteration with Error for Pseudo Contractive Mappings in Hilbert Spaces[J].Journal of Mathematics Research,2011,3(4).

[6] Dingping Wu.Asymptotically kn-strict pseudocontractive mappings in the intermediate sense[J].BCGIN,2011,EI20113814348829.

[7] Dingping Wu.The Split feasibility Problem in Hilbert Space[J].J.Engineering and Technology Research,2011.

[8] Dingping Wu.Strong Convergence Theorems for Lipschitzian Demi-cintraction[J].J.Engineering and Technology Research,2011.

[9] 王佛生,吴定平.一种求和法及其应用[J].成都信息工程学院学报,2011,26(1):57-60.

[10] Dingping Wu.Viscosity Approximation Methods for a Finite Family of Nonexpansive Non-self-mappings[J].J.Engineering and Technology Research,2011.

[11] M O Osilike,D I Igbokwe.Weak and Strong convergence theorems for fixed points of pseudocontractions and solutions of monotone type operator equations[J].Computers and Mathematical with Applications,2000,40:559-567.

[12] T Suzuki.Strong convergence of krasnoselskii and mann's type sequences for one-parameter nonexpansive semigroups without bochner integrals[J].Journal of Mathematical Analysis andApplications,2005,305:227-239.

[13] H K Xu.Viscosity approximation methods for nonexpansive mappings[J].Journal of Mathematical Analysis and Applications,2004,298:279-291.