利用ANFIS方法反演裸土区土壤水分含量

张 玲，蒋金豹，崔希民，蔡庆空

(中国矿业大学(北京)地球科学与测绘工程学院，北京 100083)

0 引言

土壤水分含量是作物长势监测和估产的主要参数［1］。传统的土壤水分获取方法难以大范围、高效率、实时和全过程地获取土壤水分参数。近年来，国内外很多学者的研究已经证明了微波遥感可以用来估算多种地形和土地覆盖条件下地表层约5 cm深度的土壤水分含量［2－6］。主动微波遥感作为土壤水分时空变化监测的一种重要技术手段，对土壤水分含量有一定的敏感性，对地物有一定的穿透能力，具有全天时、全天候的成像能力和较高的空间分辨率［7］。因此，应用微波遥感技术得到的土壤水分含量能够提高水文和气象预报模型的精度，为农业生产和灾害监测提供重要的辅助数据，在气候、气象、农业及环境灾害等领域都具有十分重要的应用价值［8］。

目前，国内外学者已采用多种算法反演裸土区的土壤水分含量。常用的经验、半经验模型主要有Dubois模型［6］、Oh 模型［9］和 Shi模型［10］等;常用的理论模型主要有Kirchhoff模型(包括物理光学模型、几何光学模型和小扰动模型)、IEM模型［11］和AIEM模型［12］等。研究表明，在采用微波遥感数据反演土壤水分的过程中，既要考虑到算法的稳定性问题，也要考虑到如何处理地表粗糙度的问题，因为在雷达系统参数不变的情况下，地表的微波散射和辐射特性依赖于土壤水分和地表粗糙度的变化［13］。目前，很多学者已将多种算法应用到土壤水分反演中:黄春林等［14］发展了一种基于集合卡尔曼滤波和简单生物圈模型的单点陆面数据同化方法，该法可以明显地提高土壤表层、植物根区以及深层土壤的水分估算精度;Chen等［15］提出了用动态学习神经网络反演地表参数的方法;Niko等［16］利用雷达数据基于T－S模糊理论反演了裸土区的土壤水分含量。针对利用多极化数据反演土壤水分过程中出现的地表粗糙度问题，金希［17］采用多波段、多极化的可变入射角数据予以减少或消除。上述研究虽然均取得了较好的试验效果，但是所用算法的稳定性需要进一步提高。为此，本文采用ALOS/PALSAR影像的HH/HV极化数据，利用自适应神经模糊推理系统(adaptive neuro fuzzy inference system，ANFIS)反演土壤水分。首先利用AIEM和Oh模型模拟地表的后向散射特性，并建立后向散射系数与地表粗糙度之间的关系;然后考虑到研究区域的实际情况，设定地表粗糙度对后向散射系数的影响为常量;在此基础上，利用ANFIS对试验数据进行拟合，直接建立HH和HV极化方式的后向散射系数与土壤水分之间的关系，以此反演土壤水分含量;最后与BP神经网络、多元线性回归、多元非线性回归方法的反演结果进行对比。

1 试验区概况及数据源

1．1 试验区概况

试验区为北京市大兴区，介于 N39．2°～39．9°，E115．7°～116．6°之间，属于中纬度区。受西风带影响，该区冬春季盛行偏北风，气候寒冷少雨雪，夏季炎热多雨，秋季天高气爽，属于暖温带半湿润气候区;多年平均降水量为568．9 mm，且主要集中在6—8月份［18］。本次试验选在2010年11月份进行，地面特征以裸地和农田为主，有少许植物覆盖，可基本近似为裸地。该地区地势平坦，土壤质地以沙土、泥土为主，其中沙土占42．1%，泥土占54．9%。

1．2 数据源

1．2．1 地表土壤水分含量和温度数据

本次试验采用土壤水分测定仪(TDR)获取地表土壤的体积含水量，TDR可直接、快速、方便、实地监测土壤水盐状况，且对土壤破坏性相对较小;采用点温计获取地表温度。试验区共布设51个样点，在每个样点周围12．5 m×12．5 m的范围内均匀采集5个点的土壤水分含量数据和地表温度数据，取这5个点的平均值作为该采样点数据。同时，利用手持GPS进行定位测量，从而得到每个样点的土壤水分含量(8% ～35%)和地表温度(8．4℃)。

1．2．2 地表粗糙度数据

地表粗糙度数据通过实地测量获取。采用的方法是剖面板法，即将剖面板插入地表，再用相机拍摄剖面板与地表的交界线，将照片数字化后在剖面上每隔一定距离取离散的点，最后用离散数据计算均方差高度和表面相关长度。本次试验测量结果显示，该地区地表粗糙度稳定，可以用地表均方根高度(s=0．8 cm)和表面相关长度(l=8 cm)来描述。

为了减少未知参数的个数，本文参考文献［13］将描述地表粗糙度的2个参数(均方根高度s和相关长度l)合并为一个参数(均方根斜度m)，即

并用m描述地表粗糙度。

1．2．3 遥感数据

试验用到的遥感数据为2010年11月14日的2景ALOS/PALSAR Level 1．5级数据，有HH与HV 2种极化方式，中心频率为1．27 GHz，影像分辨率为12．5 m，入射角为34．3°。对遥感数据进行处理并且按照

2 地表粗糙度分析

以往研究表明，裸露地表的后向散射系数σ主要受地表粗糙度和土壤水分含量的影响，具体可以表示为［10］

式中:g(m，θ)是与粗糙度相关的函数;f(ε，θ)是与土壤水分相关的函数;m为均方根斜度表示粗糙值;θ为入射角;ε为介电常数。本次试验入射角θ是固定的，为此，式(3)可以表示为

本文通过AIEM和Oh模型，构建后向散射特性数据库。根据试验区实地情况设置参数，具体设置为:土壤水分含量为2% ～40%，均方根高度为0．1～0．8 cm，相关长度为2～50 cm;地表温度根据实测结果设定。数据模拟证明，在模拟后向散射系数σHH，σHV与粗糙度的拟合关系时发现，该拟合关系与土壤水分含量无关，后向散射系数σHH，σHV与粗糙度的拟合关系如图1，2所示。

图1 HH极化后向散射系数(σHH)与粗糙度(m)关系Fig．1 Relationship between σHH and m

图2 HV极化后向散射系数(σHV)与粗糙度(m)关系Fig．2 Relationship between σHV and m

由于研究区地表粗糙度比较稳定，即均方根斜度m值基本保持不变，为此，可结合图1和图2上的关系式将与粗糙度相关的函数表示为常量，即

介电常数ε和土壤体积含水量Qv之间的关系可以用介电常数模型来描述，其表达式为［13］

式中:α，β为形状因子，其数值大小取决于土壤质地;εn为土壤复介电常数;ρb为土壤体密度，即土壤容重或者干土密度;ρs为土壤中固态物质密度(固体土壤材料的平均密度)，对于不同类型土壤，其固态物质密度差别不大，一般情况下ρb=2．66为常数;εs为土壤中固态物质介电常数且εs≈4．7;εfw为纯水的介电常数。

由式(5)可以得知，粗糙度对后向散射系数的影响为缺省值。根据实测数据，将上述土壤质地、地表温度、土壤体密度和土壤固态物质密度等变量输入式(6)，即可分别得到介电常数的实部和虚部与土壤体积含水量Qv的关系。在此，只考虑介电常数模型的实部，将模型的式子写为ε=h(Qv)，再联合式(5)，最终可建立 σHH，σHV与Qv的关系。这与Chen等［12］利用动态学习神经网络反演地表参数时所用算法的结论相同。

3 裸土区土壤水分定量反演

3．1 BP神经网络理论与ANFIS

BP(back propagation)网络是1986年由Rumelhart和McCelland等［20］为首的科学家小组提出的，是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。BP网络能学习和存贮大量的输入－输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。BP神经网络结构［21］如图3所示。

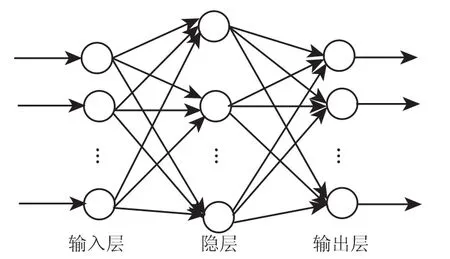
图3 BP神经网络结构示意图Fig．3 BP neutral network diagram

ANFIS是Jang［22］提出的一种将模糊逻辑和神经元网络有机结合起来的新型模糊推理系统结构，它采用反向传播算法和最小二乘法的混合算法［23］调整前提参数和结论参数，并能自动产生“if－then”规则。ANFIS的典型结构［24－25］如图4所示。其中，x1和x2是系统的输入，y是系统的输出;A1，A2，B1，B2是模糊集，如“多、少等”;ω是适用度，详情见参考文献［26］。

图4 典型ANFIS系统结构Fig．4 Typical ANFIS system structure

ANFIS系统多用于下列情况:①已经获得大量希望用于建模或是希望模型能够跟随的输入、输出数据对;②不一定需要或是不能预先得到所研究系统的基于变量特征的结构模型［26－27］。

3．2 反演模型的构建

3．2．1 基于ANFIS的反演模型

采用 ANFIS模型，以 MATLAB为平台，利用MATLAB模糊工具箱中提供的图像化工具函数anfisedit对ANFIS进行训练和检验。实验中，选取51个独立训练样本进行模型构建。每个训练样本输入部分皆为二维;对应的输出部分为一维。本系统常采用的是误差反传算法或是与最小二乘相结合的混合算法来训练相关参数。为了使系统能够更好地模拟给定的样本数据，通过减法聚类的方法自动生成初始模糊推理系统，误差阈值(error tolerance)设为0，步长设为600，采用混合学习算法训练。选择σHH和σHV作为输入因子，相对应的样本土壤体积含水量Qv作为输出因子。ANFIS网络结构如图5所示，测试误差如图6所示。

图5 ANFIS网络结构Fig．5 Network structure using ANFIS

图6 ANFIS测试误差Fig．6 Test error using ANFIS

3．2．2 基于BP神经网络的反演模型

以MATLAB为平台构建模型。根据研究区情况，将51个训练样本分成2组，作为输入数据，分别为σHH和σHV;输出数据为Qv。先对数据进行归一化处理，然后使用MATLAB对数据进行BP神经网络训练。在神经网络结构中，网络隐含层有3层，每层神经元个数设置不同，传递函数采用正切S型函数，输出函数采用线性sigmoid函数，训练函数采用带动量梯度算法，迭代步数为1 000步。BP神经网络结构如图7所示。最后，再对数据进行反归一化，得到反演结果。

图7 BP神经网络结构图Fig．7 BP neutral network structure diagram

3．2．3 基于多元线性回归的反演模型

以MATLAB为平台，在要求误差平方和为最小的前提下用最小二乘法求解参数。先做异常点分析，剔除异常点之后，再进行多元线性回归。线性回归的拟合关系式为

式中:X1代表σHH;X2代表σHV。

3．2．4 基于多元非线性回归的反演模型

对多元非线性回归模型求解的传统做法是想办法把它转化成标准的线性形式的多元回归模型来处理。本文的研究就是在分析用线性回归模型剔除异常点之后，对样本数据利用最小二乘原理进行二元二次的多项式拟合，最后求得拟合方程。多元非线性回归的拟合关系式为

式中:X1代表σHH;X2代表σHV。

4 模型精度验证

针对后向散射系数σHH和σHV，分别使用ANFIS模型、BP神经网络、多元线性回归以及多元非线性回归4种方法对数据进行拟合，构建了裸土区土壤水分含量反演模型，并把模型定量反演结果与野外实测的土壤水分含量数据进行对比(图8)。

图8 4种模型的实测与预测土壤水分含量对比Fig．8 Contrast diagram between measured and inversed soil moisture about 4 models

上述4种模型对应的均方根误差和相对误差如表1所示。

表1 4种模型反演裸土区土壤水分含量的均方根误差和相对误差Tab．1 RMSE and relative error of soil moisture inversion in bared regions using 4 model

5 结论

本文提出了一种基于ALOS/PALSAR HH和HV极化方式的后向散射系数反演土壤水分含量的方法。首先利用AIEM和Oh模型模拟地表粗糙度与后向散射系数之间的关系，然后结合实验区域地表粗糙度不变的实际情况，假定了粗糙度对后向散射系数的影响为常量，在此基础上，分别采用4种算法分别建立后向散射系数σHH，σHV与土壤水分含量的关系，进而反演出土壤水分含量。通过实验与对比分析，得出如下结论:

1)通过AIEM和Oh模型构建的后向散射系数σHH和σHV与地表粗糙度均有很好的拟合关系，可以为利用单极化方式的后向散射系数反演地表粗糙度提供参考。但在地表粗糙度几乎没有变化的情况下，可以假定粗糙度对后向散射系数的影响为缺省值，进而建立后向散射系数σHH和σHV与土壤水分的关系。

2)基于自适应神经模糊推理系统(ANFIS)、BP神经网络、多元线性回归及多元非线性回归等方法建立的半经验模型，可以反演出裸土区土壤水分的含量。结果表明，应用ANFIS反演土壤水分含量均方根误差为0．030，相对误差为14．5%，相比于其他3种方法反演的精度高。这主要是由于ANFIS方法具有收敛速度快、映射关系稳定、拟合能力和预测能力较强等优点。

需要说明的是，本次试验区地表粗糙度较为稳定，故建模时将粗糙度作为模型中的缺省值。这是本次试验误差存在的一个主要原因。另外，本研究建立的反演模型具有一定的局限性，其模型的通用性还有待于进一步研究。

［1］ 杨 虎．植被覆盖地表土壤水分变化雷达探测模型和应用研究［D］．北京:中国科学院遥感应用研究所，2003．Yang H．Radar decection model and application about surface soil moisture change in vegetabed terrain［D］．Beijing:Institute of Remote Sensing Applications，Chinese Academy of Sciences，2003．

［2］ 刘 伟，施建成，王建明．极化分解技术在估算植被覆盖地区土壤水分变化中的应用［J］．遥感信息，2005(4):3－6．Liu W，Shi JC，Wang JM．Applying the decomposition technique in vegetated surface to estimate soil moisture by multi temporal measurements［J］．Remote Sensing Information，2005(4):3－6．

［3］ 杨立娟，武胜利，张钟军．利用主被动微波遥感结合反演土壤水分的理论模型分析［J］．国土资源遥感，2011，23(2):53－58．Yang L J，Wu S L，Zhang Z J．A model analysis using a combined active/passive micro wave remote sensing approach for soil moisture retrieval［J］．Remote Sensing for Land and Resources，2011，23(2):53－58．

［4］ 田国良．土壤水分的遥感监测方法［J］．环境遥感，1991，6(2):89－98．Tian G L．Methods for monitoring soil moisture using remote sensing technique［J］．Remote Sensing of Environment，1991，6(2):89－98．

［5］ Schmugge T J．Remote sensing of surface soil moisture［J］．Journal of Applied Metheorology，1978，17:1549－1557．

［6］ Dubois P C，Van Z J，Engman E T．Measuring soilmoisture with imaging Radars［J］．IEEE Transactions on Geoseience and Remote Sensing，1995，33(4):915－926．

［7］ 杜今阳．多极化雷达反演植被覆盖地表土壤水分研究［D］．北京:中国科学院遥感应用研究所，2006．Du JY．Soil moisture inversion research using Radar in vegetabed terrain［D］．Beijing:Institute of Remote Sensing Applications，Chinese Academy of Sciences，2006．

［8］ 刘增灿．微波散射测量及土壤水分反演研究［D］．成都:电子科技大学，2006．Liu Z C．Microwave scattering measurement and soil moisture inversion［D］．Chengdu:University of Electronic Science and Technology of China，2006．

［9］ Oh Y，Sarabandi K，Ulaby F T．An empirical model and an inversion technique for Radar scattering from bare soil surfaces［J］．IEEE Transactions on Geoseience and Remote Sensing，1992，30(2):370－381．

［10］ Shi JC，Wang J，Hsu A Y，et al．Estimation of bare surface soil moisture and surface roughness parameter using L－band SAR image data［J］．IEEE Transactions on Geoseience and Remote Sensing，1997，35(5):1254－1266．

［11］ Fung A K，Li Z，Chen K S．Backscattering from a randomly rough dielectric surface［J］．IEEE Transactions on Geoseience and Remote Sensing，1992，30(2):356－369．

［12］ Chen K S，Wu T D，Leung，et al．The emission of rough surfaces calculated by the integral equation method with a comparison to a three－dimensional moment method simulations［J］．IEEE Transactions on Geoscience and Remote Sensing，2003，41(1):90－101．

［13］ 赵天杰，张立新，蒋玲梅，等．利用主被动微波数据联合反演土壤水分［J］．地球科学进展，2009，24(7):769－775．Zhao T J，Zhang L X，Jiang LM，et al．Joint inversion of soil moisture using active and passive microwave data［J］．Advances in Earth Science，2009，24(7):769－775．

［14］ 黄春林，李 新．基于集合卡尔曼滤波的土壤水分同化试验［J］．高原气象，2006，25(4):665－671．Huang C L，Li X．Experiments of soil moisture data assimilation system based on ensemble Kalman filter［J］．Plateau Meteorology，2006，25(4):665－671．

［15］ Chen K S，KaoW L，Tzeng Y C．Retrieval of surface parameters using dynamic learning neutral network［J］．International Journal of Remote Sensing，1995，16(5):801－809．

［16］ Niko E C，Verhoest B，De B，et al．A Takagi－sugeno fuzzy rule－based model for soil moisture retrieval from SAR under soil roughness uncertainty［J］．IEEE Transactions on Geoscience and Remote Sensing，2007，45(5):1351－1360．

［17］ 金 希．高分辨率SAR影像裸土信息提取及土壤含水量反演初探［D］．杭州:浙江大学，2011．Jin X．A preliminary study on bare soil extraction and its moisture retrieval resolution SAR data［D］．Hangzhou:Zhejiang University，2011．

［18］ 吴 敏，冯绍元，孙春燕，等．北京市大兴区典型土壤水分入渗规律田间试验研究［J］．中国农业大学学报，2009，14(4):98－102．Wu M，Feng SY，Sun C Y，et al．Field experimental study on soil infiltration process of Daxing District，Beijing［J］．Journal o f China Agricultural University，2009，14(4):98－102．

［19］ Masanobu Shimada．PALSAR radiometric and geometric calibration［J］．Geoscience and Remote Sensing，2009，47(12)，3915－3932．

［20］ Rumelhart D E，Hinton G E，McClelland JL．A general framework for parallel distributed processing［C］//Parallel Distributed Processing:Exploratiens in the Microstruc true of Cognition Cambridge，MA，USA:MIT Press，1986:45－76．

［21］ Robert H N．Theory of the backpropagation neutral network［C］//International Joint Conference on Neutral Network Washington D C．1989，1:593－605．

［22］ Jang R．ANFIS:Adaptive－Network－based Fuzzy Inference System［J］．IEEE Transactions on Systems，Man and Cybernetics，1993，23(3):665－685．

［23］ 李 志．模糊神经推理系统_ANFIS在散货船运力预测中的应用研究［D］．大连:大连海事大学，2000．Li Z．Research on predictive capability of a new Neuro－Fuzzy inference system－ANFIS on the tonnage suppy and deliveries of world bulk fleet［D］．Dalian:Dalian Maritime University，2000．

［24］ Lauren M K，Smith JM，Moffat J．Using the fractal attrition equation to constract a meta model of the MANA cellular automaton combat model［R］．The Technical Cooperation Program Report，2005．

［25］ Ingber L，Sworder D D．Statistical mechanics of combat with human factors［J］．Mathematical and Computer Modelling，1991，15(2):99－127．

［26］ 顾秀萍．自适应神经模糊推理系统(ANFIS)及其仿真［J］．火力与指挥控制，2010，35(2):48－53．Gu X P．Study on the adaptive network－based fuzzy inference system and its simulation［J］．Fire Control and Command Control，2010，35(2):48－53．

［27］ 吴晓莉，林哲辉．MATLAB辅助模糊系统设计［M］．西安:西安电子科技大学出版社，2002．Wu X L，Lin Z H．MATLAB fuzzy system design［M］．Xi’an:Xi’an Electronic and Science University Press，2002．