基于梯度域的高辐射分辨率遥感图像动态范围压缩算法

王振国，李少敏，曲广兵

(中国人民解放军96635部队，天津 300350)

0 引言

现代遥感技术的日益发展，促使遥感信息获取平台和成像系统的水平不断提高，特别是遥感图像的空间分辨率、辐射分辨率、光谱分辨率和时间分辨率都在不断提高，使得高质量遥感数据的应用已经从单纯的定性应用向定量应用的方向发展［1］。目前，人们常用的航天航空数字传感器(如IKONOS，ALOS，IRS，Quick Bird以及ADS40数字航空相机等)所获取的数字遥感图像的辐射分辨率都在11 bit或者14 bit以上［2］。利用高辐射分辨率遥感图像(high radiation resolution remote sensing image，HRRRSI)，人们可以更加精细和准确地得到各类地物的细节结构和光谱信息，从而可有效地降低混合像元对定量遥感分析结果的影响，进一步提高定量遥感分析的精度，为定量遥感分析的广泛应用奠定基础。然而，与一般的8 bit遥感图像相比，HRRRSI图像的利用在许多方面都存在特殊之处，其中最直观的也是最常见的问题就是对HRRRSI的显示问题。现在常用的做法是将HRRRSI进行压缩后显示，常用的高动态域(high dynamic range，HDR)辐射图像的显示方法分为全局映射和空间变化2类。人们将前者作为色调再现曲线(tone reproduction curves，TRC)，将后者作为色调再现算子(tone reproduction operators，TRO)。对于多数的TRC方法，都是将HDR值进行线性分级，进而将图像的像元值映射到设定的范围之中(比如常见的图像取值范围［0，1］);现在常见的TRC方法主要有亮度校正和直方图均衡化等，该方法可以较好地保留原始图像像元之间的比例关系，但会降低所显示图像中比原始图像动态范围小的影像清晰度。针对上述问题，本文就HRRRSI显示问题，提出了一种基于梯度域动态范围压缩的图像增强和显示算法，能够明显改善遥感图像的显示效果。通过与常用的线性拉伸处理显示效果对比，进一步验证了本文算法的可行性和有效性。

1 高动态范围图像的显示

目前，HDR辐射分辨率的数字图像越来越受到计算机图像处理和应用领域的青睐，应用范围越来越广。可以预测，随着现代数字图像技术的日益发展，未来的数字相机就能够直接获取HDR图像和视频［3－4］。

与常用的低动态域图像相比，HDR图像拥有诸多优点［5］，且已有的应用都证明了HDR图像具有广阔的应用前景［6－7］。不过，HDR 图像在应用中也遇到一定问题，就是在不同类型的普通显示器上显示的HDR图像的动态域要比真实场景的动态域小很多;所以，针对现在普遍采用的低动态域显示设备，就需要对其显示HDR图像的方法进行深入研究。

图1示出辐射分辨率为14 bit的高辐射分辨率航空遥感图像在低动态域显示设备上的显示结果。

图1 辐射分辨率为14 bit的航空遥感图像显示结果Fig．1 Displaying results for airborne remote sensing image with 14 bit radiation resolution

从图1中可以看出HDR图像在普通显示设备上进行显示时出现的问题:在直接显示的原始图像(图1(a))中，影像细节信息没有得到很好的展现;而经过Photoshop软件拉伸处理后的显示结果(图1(b))虽然比图1(a)有了较大的改进，但所显示的影像细节信息也不是特别完美。由此可见，在一般的显示设备上对14 bit的HDR图像进行显示会存在一定的问题，其原因主要是一般显示设备的动态范围通常低于100∶1。

因此，本文针对HRRRSI显示问题，提出了一种对HDR压缩图像进行显示的增强算法，以便能够在一般的显示设备上对HDR图像进行完美显示。实验结果表明，该算法理论简单、运算效率高、效果较好。

2 梯度域动态压缩

本文算法是建立在一个被人们所广泛接受的假设［8］的基础上，即人类的视觉系统对视网膜所接受到的亮度变化并不敏感，但对对比度的局部变化比较敏感。该算法还基于一个必要的前提，即对于HDR图像而言，其亮度的显著变化一定会在某些尺度上产生较大的亮度梯度，而细节信息则通常都对应比较小的亮度梯度。故本文算法的基本思路就是通过对不同尺度上较大亮度的识别，在保持其方向不变的情况下减小其量值;同时保证对较大尺度的衰减程度要大于对较小尺度的衰减程度，这样，就可以在压缩亮度变化范围的同时，对图像的细节信息给予保留。同时，对经过压缩后的HDR图像还可以在衰减的梯度域中进行重建。

需要补充说明的是，本文算法的实现和计算过程都是针对图像亮度值的对数来完成的，而非直接针对亮度值本身完成。这里采用图像亮度值的对数来进行计算的原因主要为:①亮度的对数能够较好地对感知到的光线亮度进行近似;②对数域中的梯度能够对应于亮度域的局部亮度。

为了对本文算法进行说明和解释，首先对一维情况下的算法原理进行简述。

给定一个高动态范围的一维函数，用H(x)表示该函数的对数。如上所述，本文算法的目标是在保持较小局部变换的同时，压缩H中较大的数值变化。此目标是通过把一个空变衰减映射函数Ф应用到导数H'(x)来完成的，即

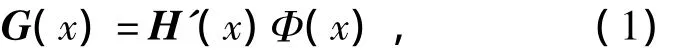
式中:G为衰减后的导数;H'为原始导数;Ф为空变衰减映射函数。G的符号与H'相同，但H'的大小被一个由Ф所决定的因子改变;Ф设计用于更多地衰减较大的导数。事实上，如下面所解释的那样，Ф在不同尺度上代表不同的导数值。

现在可以通过对压缩后的导数求积分来构建一个简化的动态域函数I(另有一个附加常数C)，即

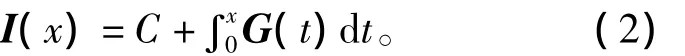
最后，对上式的结果进行幂运算就可得到亮度函数。整个过程如图2所示。

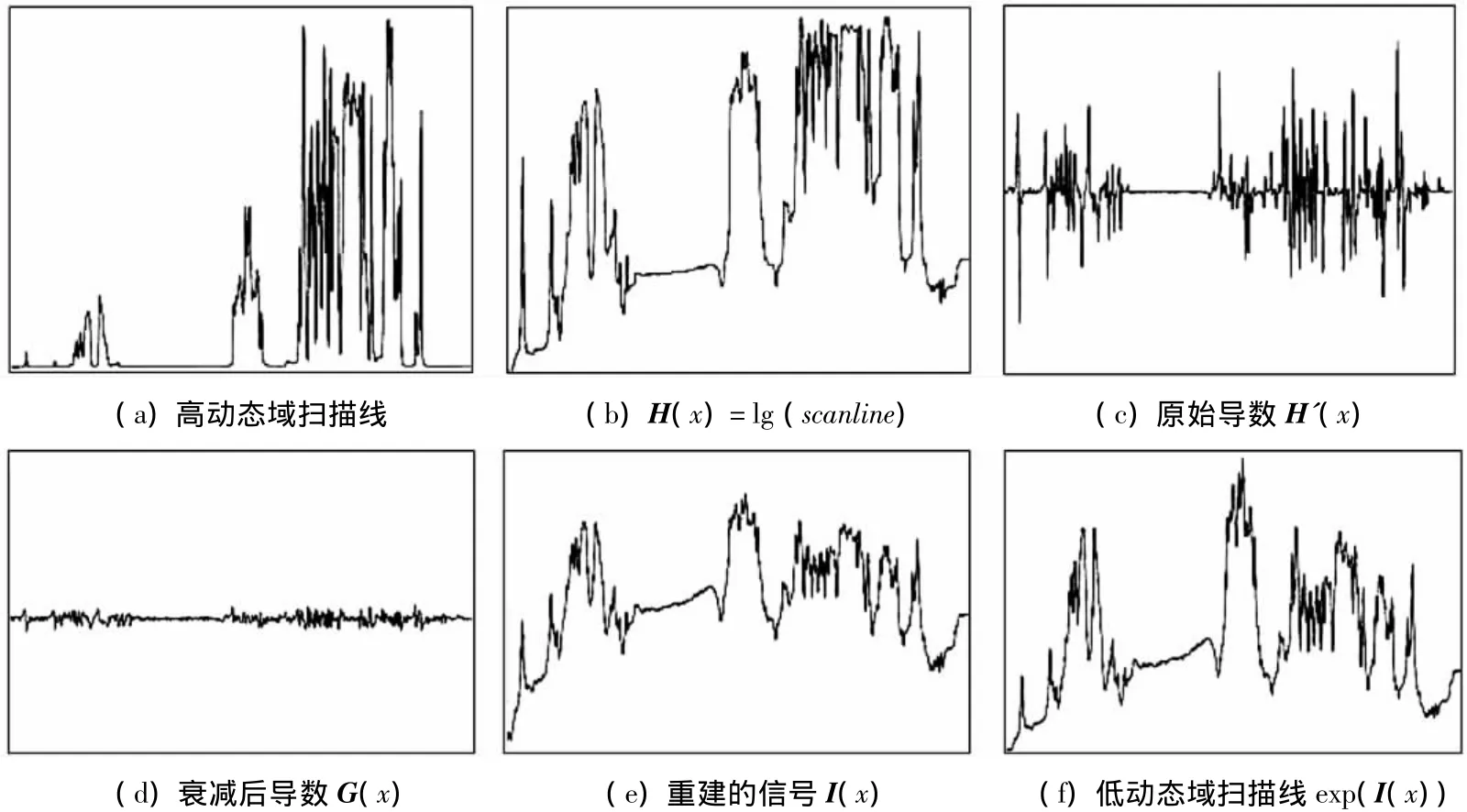
图2 一维扫描线衰减前后导数变化对比Fig．2 Comparison between derivative changes before and after attenuation of one dimensional scanning line

图2(a)为一条动态范围为2 415∶1的高动态域一维扫描线(scanline);图2(b)为图2(a)的对数，即H(x)=lg(scanline);图2(c)为图2(b)的原始导数;图2(d)为衰减后的导数G(x);图2(e)为重建的信号I(x)(如式(2)中所定义);图2(f)为一条低动态域扫描线exp(I(x))，其新的动态范围为7．5∶1。从图2(a)和图2(f)中2条扫描线的动态范围对比中可以看出，后者的动态范围远远小于前者，这样更便于对扫描线的对比显示;对应到二维图像上，则动态范围较低的图像更容易在低动态域设备上得到较好的显示效果。应该注意的是，每个示意图中垂直轴的尺度并不一样，只有图2(c)和图2(d)中的垂直轴的尺度一致，这是为了更好地对比衰减前后导数的变化。

为了将上述方法扩展到二维HDR函数中H(x，y)，本文采用梯度▽H代替导数。为了避免将空间失真引入到图像中，只改变梯度的量值，而不改变其方向。因此，与一维情况相似，可以计算

与一维情况不同的是，不能简单地通过对G求积分得到一个压缩后的动态域图像，因为该函数不一定是可积的;也就是说，可能并不存在使G=▽I的图像I。事实上，势函数(potential function)的梯度(以二维为例)必须是一个守恒场［9］。换言之，梯度▽I=(∂I/∂x，∂I/∂y)必须满足

但是，对于G而言，这种情况很少见。

解决上述问题的一个可能的办法是将G垂直投影到一个有限的、能够生成可积矢量场的规范正交基函数集上(如傅立叶基函数)［10］。在本文算法中，使用了一个更直接、也更有效的方法，即寻找在最小二乘框架下梯度最接近G的函数I所有的二维势函数空间。换言之，I应该能够使得积分

最小化，式中

根据变分原理，使积分最小化的函数I满足欧拉－拉格朗日方程，即

这是一个I中的偏微分方程。替换F可以得到

公式(8)两边除以2并化简，可得到泊松方程

式中:Δ2为拉普拉斯算子，即

div G为向量场G的散度，定义为

3 梯度衰减函数

本文算法利用Φ(x，y)的一个因子在各个像元上对HDR的图像梯度进行衰减，从而实现HDR压缩;并希望衰减能够依次进行，且较大梯度的收缩比小梯度的收缩更大。

真实图像中包含所有尺度的边缘。因此，为了可靠地探测所有重要的强度变化，必须采用多分辨率边缘探测的方法。然而，不能简单地在探测到的分辨率图像上对各个梯度进行衰减，这可能会在锐利边缘周围产生光环效应(如第2节所提到的那样)。解决的方法是将合适的衰减从被探测的那个尺度扩展到全分辨率图像。因此，所有梯度处理都在单分辨率尺度上进行，这样就不会产生光环效应。

首先，需要构造一个高斯金字塔 H0，H1，…，Hd，其中:H0是全分辨率HDR图像;Hd是金字塔中的最低一级图像。d的选取标准为使Hd的宽度和高度不小于32。在第k层上利用中心差分公式来计算梯度，即

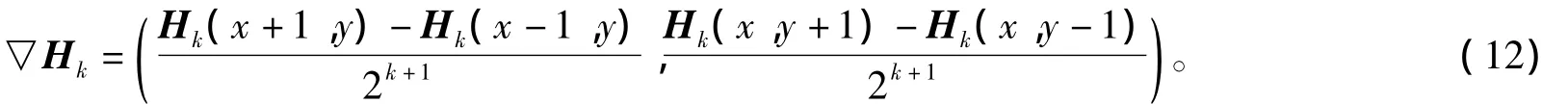
第k级上的一个尺度因数φk(x，y)由此尺度上的像元梯度值所决定，即

它是带有2个参数的函数族。第一个参数α决定了哪个梯度值没有改变。较大的梯度被衰减(假定β＜1)，而小于α的梯度值则被稍微放大。本文设置α为平均梯度值的0．1倍，β取值在0．8～0．9之间。

全分辨率梯度衰减函数Φ(x，y)采用自上而下的方式进行计算，计算方法是用线性内插将比例因数φk(x，y)由某一级扩展到下一级，并利用逐点相乘法将其累积。这个过程可通过求解方程组E，即

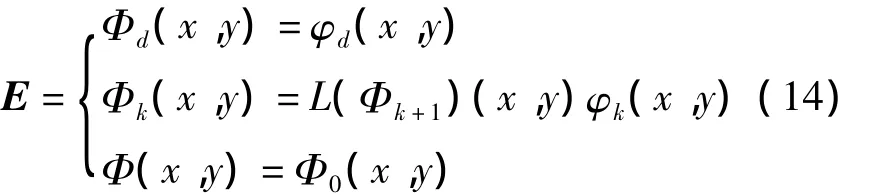
来实现。式(14)中:d为最低一层;Фk为在第k级所累积的衰减函数;L为线性内插中的一个采样算子。计算结果中，在最佳层次上每个像元的梯度衰减是由所有通过该像元的边缘(来自不同级别)强度来决定的。

4 算法应用

为了求解式(9)中的微分方程，必须首先确定边界条件。在本文的例子中，最直接的选择是诺伊曼(Neumann)边界条件，即▽I·n=0(垂直于边界方向的导数为0)。

由于拉普拉斯算子Δ2和div都是线性算子，所以利用标准有限差使其近似服从一个线性方程系统。具体地说，可以利用近似方程

在全分辨率图像中，将像元栅格间距定为1;而对于 梯度▽H，可使用前向差分来近似得到，即

对于div G，则可使用后向差分来近似得到，即

这样，就确保了前向和后向差分的组合使用对div G的近似与使用拉普拉斯的中心差分方法是一致的。

在边界处可采用同样的定义，但要假设原始图像栅格周围的导数为0。例如，对于图像左边边界的每个像元有方程成立。

有限差分方案可产生一个大的线性方程系统——每个方程对应于图像中的一个像元，但相应的矩阵在每行只有5个非零元素，因为每个像元只和它周围4个像元相邻。本文通过全多格网算法(full multi－grid algorithm)和高斯－塞德尔平滑迭代法来解算该方程系统。这样，要得到一个近似的解，需要大约O(n)步运算(n为图像中的像元个数)。另外一个选择是使用“快速泊松解法”，它是用快速傅立叶变换来对拉普拉斯算子进行求逆;然而，这个算法的复杂度可能是O(nlgn)步运算。

5 实验结果与分析

为了验证本文提出的基于梯度域的高动态范围压缩算法的效果，本文通过对一景由ADS40数字航空相机摄取的高辐射分辨率遥感图像进行试验和分析，图像大小为512像元×512像元，图像的辐射分辨率为14 bit。试验结果如表1、图1和图3所示。

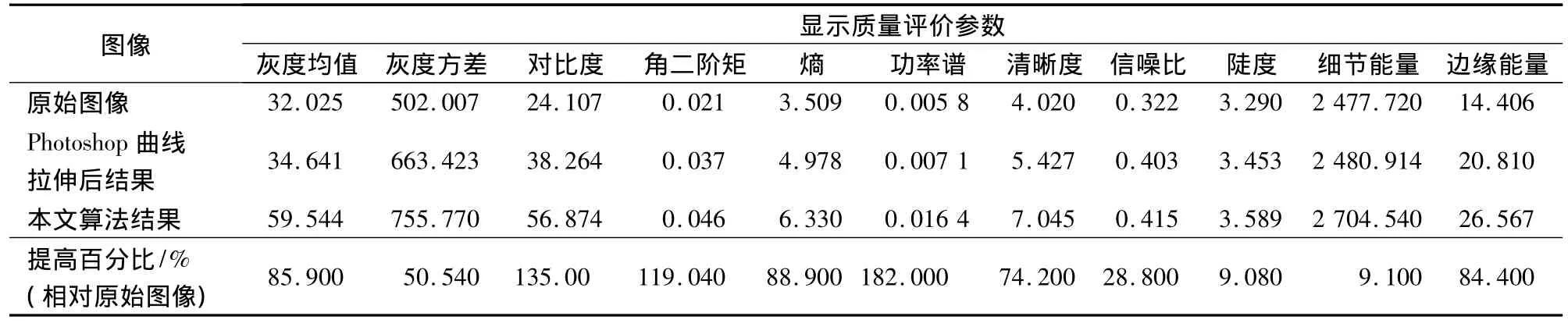
表1 图3中不同结果图像显示质量评价参数Tab．1 Evaluation parameter list of displaying quality for different mages in Fig．3

图3 辐射分辨率为14 bit的航空遥感图像本文方法显示结果Fig．3 Displaying result using the method in this paper for airborne remote sensing image with 14 bit radiation resolution

比较图1和图3可以看出，在直接显示的原始图像(图1(a))中几乎看不到影像细节信息;在利用Photoshop软件中的线性拉伸功能处理过的图像(图1(b))中虽然可以看出部分影像细节信息，但阴影部分的信息却显示不出来;而在利用本文算法处理后的图像(图3)中则可以清楚地看到影像信息和阴影部分的细节结构信息(如油罐和灌木林阴影范围内的细节结构)。表1中列出的不同结果图像显示质量评价参数也验证了本文算法的有效性。

6 结论

1)本文针对高辐射分辨率遥感图像在普通显示设备上的显示问题，通过对高辐射分辨率的特性分析，提出了对其图像显示结果进行增强的有效算法。该算法通过对高辐射分辨率图像中大梯度域的梯度衰减来实现，能够在常用的显示设备上对高辐射分辨率遥感图像的细节信息进行精确显示。

2)经过有针对性的实验表明，本文算法能够实现对高动态范围图像的完美显示，同时还能够很好地保留图像的细节信息和抑制图像中存在的边缘效应。

［1］ Mugnier L M，Robert C，Conan JM，et al．Myopic deconvolution from wave－front sensing［J］．Journal of Optics Engineering，2001，18(4):862－872．

［2］ 朱述龙，朱宝山，王红卫．遥感图像处理与应用［M］．北京:科学出版社，2006．Zhu SL，Zhu B S，Wang H W．The processing and application of remote sensing images［M］．Beijing:Science Press，2006．

［3］ Schechner Y Y，Nayar S K．Generalized mosaicing［C］//Proceedings of the 8th IEEE International Conferences on Computer Vision．Vancouver，BC:IEEE，2001，I:17－24．

［4］ Nayar SK，Mitsunaga T．High dynamic range imaging:Spatially varying pixel exposures［C］//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition．Hilton Head Island，SC:IEEE，2000:472－479．

［5］ 关元秀，程晓阳．高分辨率卫星影像处理指南［M］．北京:科学出版社，2008．Guan Y S，Cheng X Y．The processing guide for high resolution satellite images［M］．Beijing:Science Press，2008．

［6］ Debevec P．Rendering synthetic objects into real scenes:Bridging traditional and image－based graphics with global illumination and high dynamic range photography［C］//In Proc．ACM SIGGRAPH 98，MCohen，Ed，1998:189－198．．

［7］ Cohen J，Tchou C，Hawkins T，et al．Real－time high dynamic range texture mapping［C］//Gortler S J，Myszkowski K．Eds Springer－Verlag，in Rendering Techniques，2001:313－320．

［8］ Dicarlo JM，Wan dell B A．Rendering high dynamic range images［C］//In Proceedings of the SPIE:Image Sensors，2001，3965:392－401．

［9］ Harris JW，Stocker H．Handbook of mathematics and computational science［M］．New York:Springer－Verlag，1998．

［10］ Frankot R T，Chellappa R．A method for enforcing integrability in shape from shading algorithms［C］//IEEE Transactions on Pattern Analysis and Machine Intelligence，1988，10(4):439－451．