加肋土工膜与砂性土界面相互作用机制分析
2012-12-31高俊丽张孟喜林永亮邱成春
高俊丽,张孟喜,林永亮,邱成春
(上海大学 土木工程系,上海 200072)
1 引 言
针对填埋场衬垫系统中土与土工合成材料界面以及土工合成材料与土工合成材料界面强度较低,构成了填埋场中的薄弱面,影响了填埋场的安全稳定性[1-5],本文提出一种新型土工合成材料——加肋土工膜来增加界面剪切强度。目前国内外已有许多专家对土工膜与砂土或与加肋土工膜结构较为相似的土工格栅与砂土界面的相互作用机制做了大量研究。Jewell 等[6]提出了土工格栅被动阻力的一般表达式,并在不同假设条件的基础上,对承载力系数进行了理论研究,获得了理论公式。Dyer[7]利用光弹法测量出了拉拔试验中在格栅横肋前发展的被动应力楔形区,通过光弹法得到的图片证明了土工格栅与土相互作用的复杂性。Koerner 等[8]研究了在筋土界面发生剪切变形过程中,会导致沿平行于相对位移方向的加筋材料平面上的摩擦阻力和垂直于相对位移方向的格栅横肋上的被动阻力两个剪应力分量。Irsyam 等[9]利用热蜡通过直剪试验对土工格栅进行了研究,得出了松砂和密砂在不同横肋间距下的剪切面,提出了横肋端承阻力的计算公式和剪切面的理论值。Jacob 等[10]对光面土工膜与砂土界面的本构模型进行了研究,指出了界面剪应力的理论表达式。
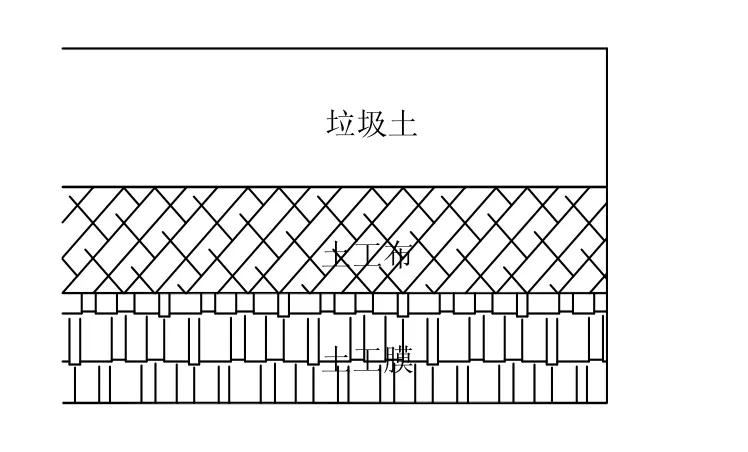
图1 多层衬垫系统示意图 Fig.1 Schematic diagram of the layer components of the interface shear tests with overburden materials
笔者前期对加肋土工膜与砂性土界面做了43组直剪试验,得出加肋土工膜能有效提高界面的抗剪强度,但对加肋土工膜与砂性土界面的作用机制还有待进一步地深入研究。本文在原有加肋土工膜与砂性土界面直剪试验结果的基础上[11-12],借鉴以往的研究成果[13-22],建立加肋土工膜-砂性土界面的力学模型,分析加肋后界面剪切强度提高的影响因素。得到加肋土工膜与砂性土界面的抗剪强度主要由面摩擦应力、侧摩擦应力和端承阻应力3 部分组成,并给出了具体的表达式。
2 直剪试验
2.1 试验设备
该设备是在现有大型直剪仪的基础上对剪切盒进行改装而成的。试验的垂直和水平荷载分别由空气压力系统和电动机提供,通过高精度的荷载和位移传感器,将试验数据传输到数据采集系统,如图2 所示。

图2 大型剪切/拉拔仪 Fig.2 Large scale direct shear/pullout apparatus
2.2 试验材料
试验用砂性土和土工膜为材料,其物理力学性质如下所述。
2.2.1 砂性土
为了减少填料水分对试验结果的影响,试验采用相对密度为干砂试样。其物理性质指标:密度为1.69 g/cm3,颗粒相对密度为2.65,含水率为0.12%,孔隙比为0.57,试验时砂性土的相对密度为0.775,其颗粒级配见表1。

表1 砂性土的颗粒级配 Table 1 Grain size distribution of sandy soil
2.2.2 加肋土工膜
加肋土工膜具体布置如图3 所示,在母模上按一定方式粘贴肋块,所加肋片是相同材质和厚度的土工膜,其中,块状肋块的尺寸为15 mm×20 mm,条状肋块的尺寸为15 mm×200 mm,肋块沿剪切方向按一定间距s 布置,分1 排、2 排、3 排、4 排共4 种布置形式,其特点是长边和短边方向均非满布布筋、竖直方向高度不变。
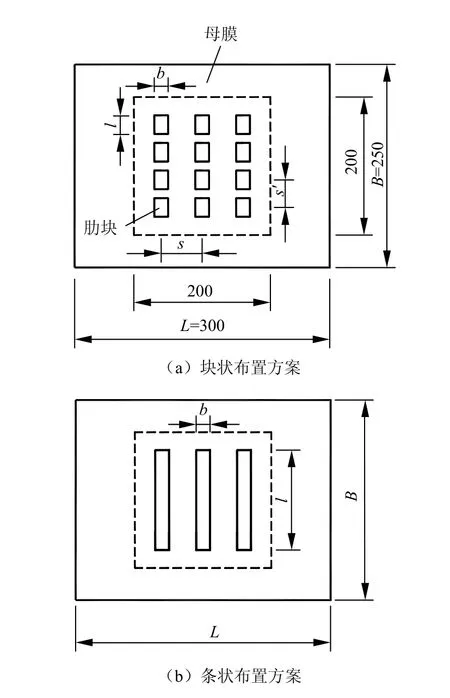
图3 加肋土工膜布置方案(单位:mm) Fig.3 Experimental schemes for reinforcement (unit: mm)
2.3 试验结果
加肋土工膜与砂土界面典型剪应力-剪切位移曲线见图4。从图中可以看出:其曲线基本呈双曲线,不同法向应力下剪应力-切位移曲线变化趋势大致相同,即在受力初期,剪应力随着剪切位移的增长而迅速增长,在剪切位移达到2.5~3.5 mm 后,随着剪切位移的增加,剪应力增长趋势减缓,且均发生了应变硬化现象,法向应力越大,硬化现象越显著。
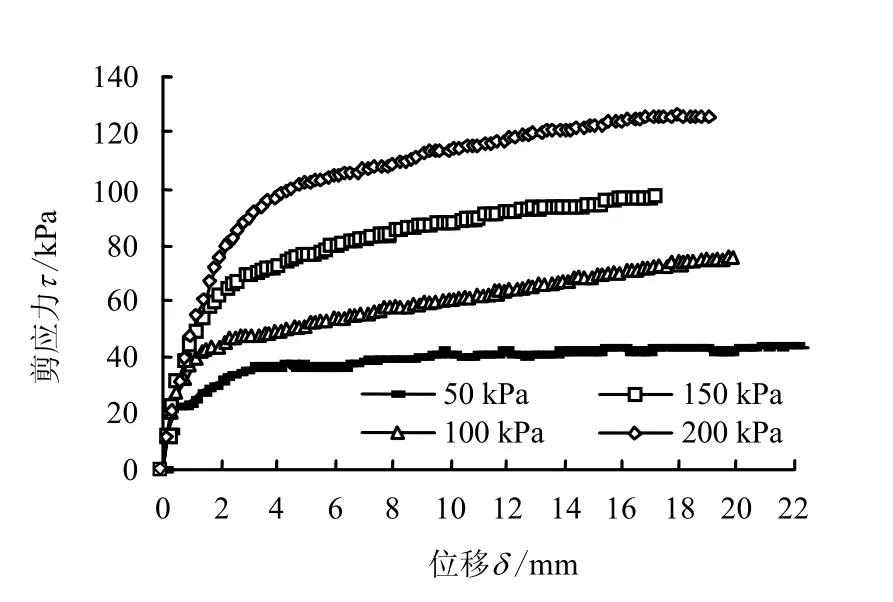
图4 加肋土工膜与砂性土界面典型剪应力-剪切 位移曲线(两排块状) Fig.4 Typical shear stress-shear displacement curves for reinforced geomembrane and sand interface (double lump)
3 破坏形态分析
结合前面加肋土工膜与砂性土界面直剪试验结果,现对试验后试样的破坏形态进行分析(如图5 所示)。从图中可以看出,粘贴在母膜上的肋块不能完全牢固地固定,部分肋块发生了移位、弯曲(见图5(a)、(b)),或者母膜端部孔洞发生了拉伸变形(见图5(c)),或者母膜本身拱起(见图5(d))。一般来讲,肋块移位、弯曲,母膜端部孔洞变形,母膜本身拱起这几种情况不会同时发生,也不会出现在相同的部位。
从图5(a)、(b)中可看出,条状肋块发生了很明显的移位和变形,这可以通过下面机制进行分析:与界面接触的砂性土在法向应力作用下,将产生侧向位移,但由于前方肋块的限制,致使砂性土的运动受到限制,从而使砂性土受到挤压,进而影响到肋块的受力和变形。此外,由于肋块所包围的挤密区土体的作用力不至于短时间内达到最大值,有一个逐步发展的过程,从而肋块的作用得以充分发挥。
4 界面阻力分析
4.1 界面总阻力
本文涉及的加肋土工膜由光面土工膜和若干个肋块组成,是一个具有空间特性的土工膜结构,这导致加肋土工膜与砂性土之间的相互作用机制远比光面土工膜、土工织物等平面材料要复杂。考虑到加肋土工膜-砂性土界面与土工格栅-砂性土较为接近,在现有对土工格栅的受力机制受力分析的基础上,提出加肋土工膜与砂性土界面的剪切力由3部分组成:土工膜表面和肋块表面与砂性土之间的面摩擦力fF 、肋块端部的端承阻力bF 和肋块侧面的侧摩擦力pF (如图6 所示),即:

图5 加肋土工膜破坏图 Fig.5 Failure situation of specimens
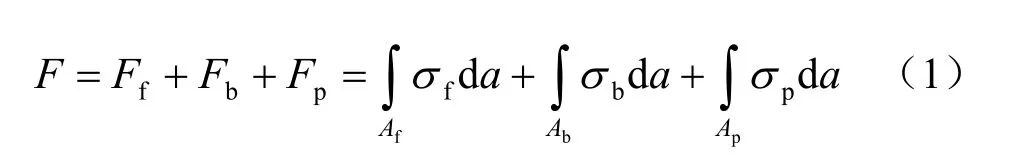
式中:fF 、bF 、pF 分别为界面面摩擦力、肋块端承阻力和肋块侧摩擦力(N);fσ 、pσ 、bσ 分别为界面面摩擦应力、肋块端承阻应力和肋块侧摩擦应力(MPa);fA 、bA 和pA 分别为土工膜有效表面积、肋块端部总面积和肋块侧面总面积(m2)。
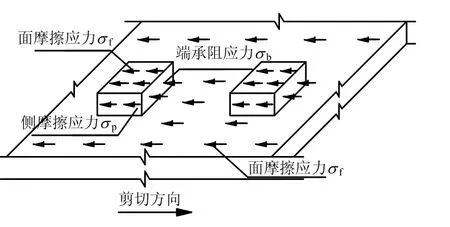
图6 加肋土工膜与砂性土界面作用机制 Fig.6 Interface mechanism between reinforced geomembrane and sand
4.1.1 面摩擦应力分析
加肋土工膜埋置于砂性土内,在法向应力的作用下,加肋土工膜与砂性土接触的界面上将产生摩擦应力。该摩擦应力沿剪切方向并非均匀分布,随各点的应变不同而有所不同。但当加肋土工膜移动的瞬间,加肋土工膜与砂性土界面的摩擦应力可认为是均匀分布,该值即为界面的摩擦强度。在现有的国内外文献中,对面摩擦应力的研究已经比较成熟,可以用下式表示:

式中: f 为底部土工膜(母膜)与砂性土界面摩擦系数; σn为界面所受法向应力, σn= σ0+γD (kPa); σ0为γ 为上剪切盒内砂性土的重度(kN/m3);D 为界面距承压板底部的有效高度(m)。
4.1.2 侧摩擦应力分析
由图6 可知,块状土工膜上的块状肋块与砂性土还存在侧摩擦应力pσ 的作用,其计算采用与面摩擦应力相同的办法,其公式为

4.1.3 端承阻应力分析
在既有直剪试验及破坏试样分析的基础上,对单个肋块所受端承阻应力进行分析,考虑到实际受力的复杂性,先提出以下基本假定:
(1)土工膜有足够的强度和刚度,视为理想刚体,砂性土体为理想的摩尔-库仑材料;
(2)不计肋块端承阻应力对面摩擦应力的影响;
(3)前、后两排肋块之间留有充足的距离以保证互不影响;
(4)界面受到水平向剪力作用后,根据力的相互作用原理,肋块将对其后的砂性土产生一个大小相等的反作用力rp ,由于肋块较薄,对于单个肋块,可假定其上所受水平应力是均匀分布的,如图7 所示。
对于单个肋块,从极限平衡边值问题的角度考虑,可将肋块受到端承阻应力后的滑移线如图8 所示划分,具体说明如下:
对于Ⅰ区,其已知边界为光滑界面线,是要求由已知边界的x、z、σ 、θ 来计算未知边界的x、z、σ 、θ ,故其属于柯西边值问题;对于Ⅱ、Ⅳ区,其已知边界为两个滑线,是要求由两个已知边界的x、z、σ 、θ 来计算土体中滑线的x、z、σ 、θ ,故属于古尔萨边值问题;对于Ⅲ、Ⅴ区,其已知边界为滑线,而未知边界可以知道部分条件,故其属于混合边值问题。
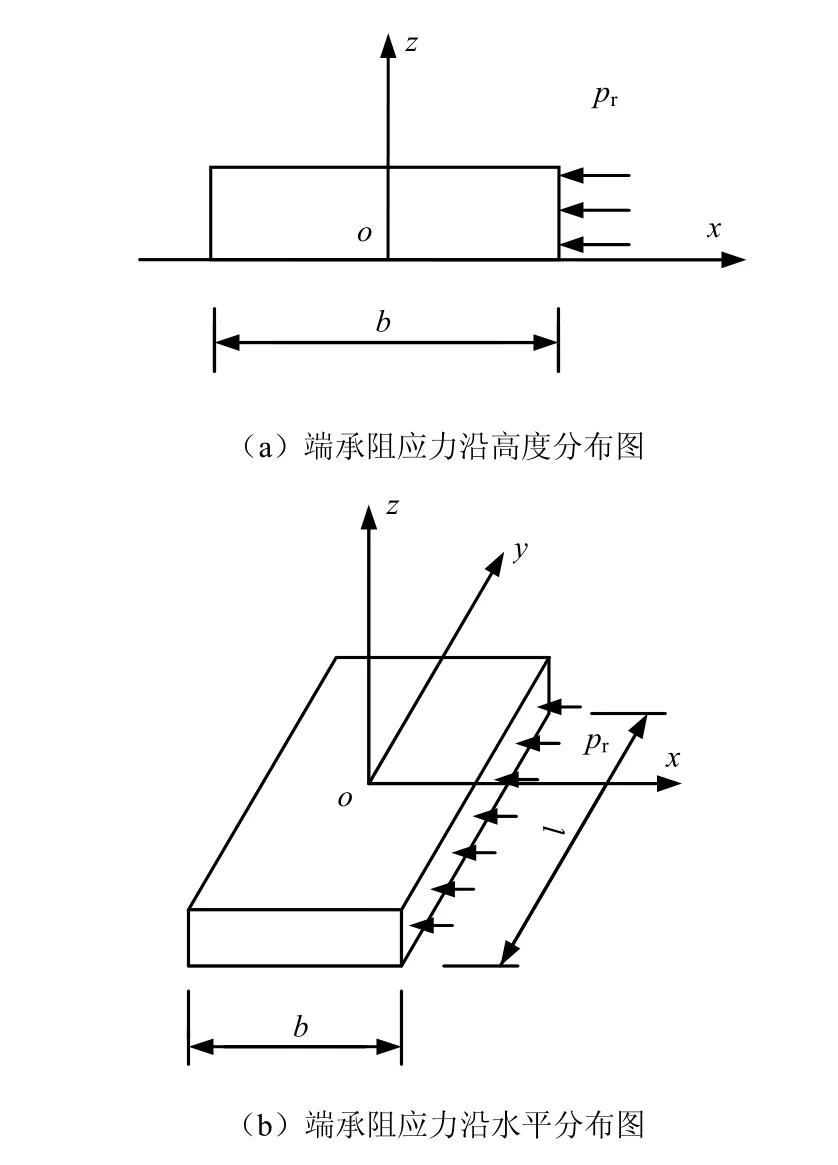
图7 肋块受水平力的分布图 Fig.7 Horizontal force distribution of reinforcement
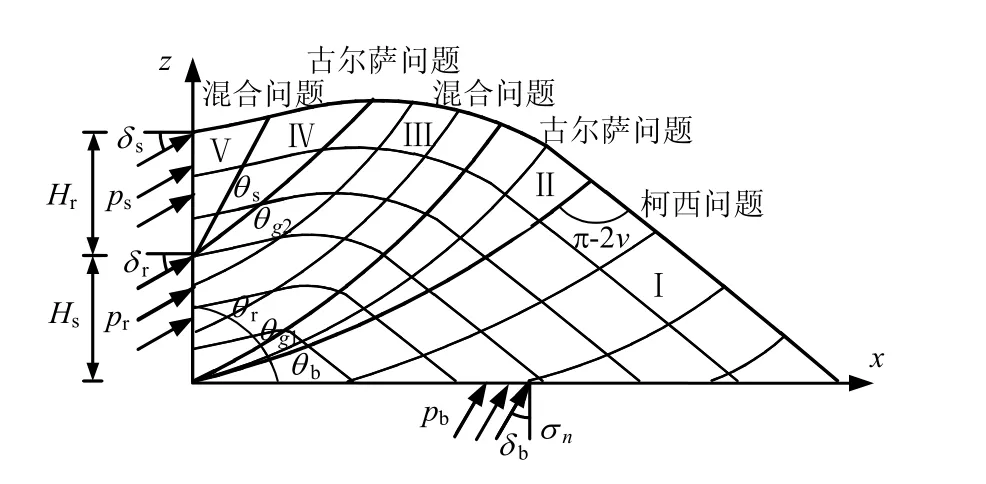
图8 肋块端承阻应力受力分析图[1] Fig.8 Analysis chart of bearing resistance
母膜上受力bp 为,

式中:bδ 为母膜与砂性土界面的似摩擦角。 由于底部接触面区域是属于柯西边值问题Ⅰ区,主动作用力占有主导优势,则 1k =+ ,得
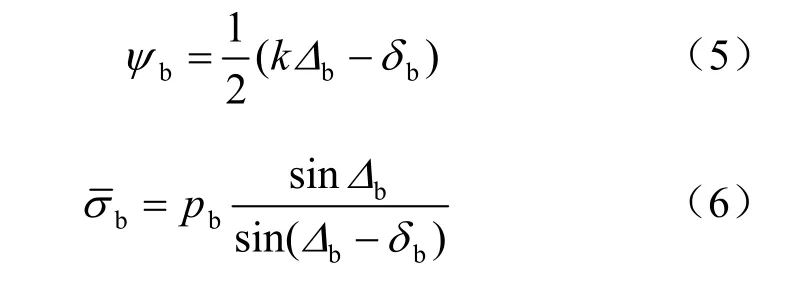
其中:

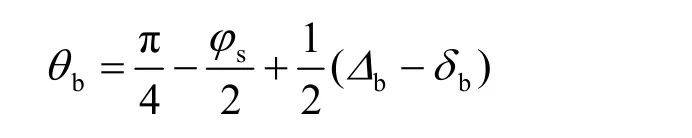
肋块端部所受应力rp 为

式中:rδ 为肋块端部与砂性土界面似摩擦角,rσ 为作用该界面上的法向应力。
肋块端部与砂性土界面在混合边界区域Ⅴ区,该区被动土压力占主导地位,有 1k =- ,得
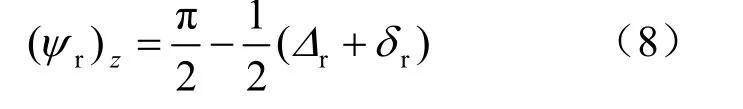
其中,rψ 是以z 轴作为参考坐标的,如果以x轴作为参考坐标,则有
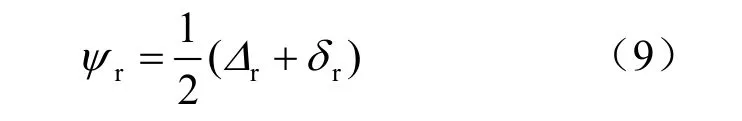
那么肋块端部与砂性土界面所受法向应力为
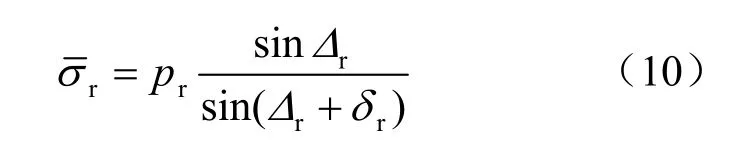
其中:
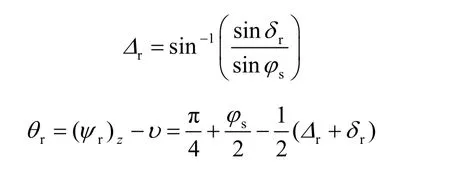
在直剪试验过程中,由于肋块上方有部分砂性土在法向应力作用下,将形成一个刚性砂性土区域,可将其定义为刚性区域,如果刚性区域与砂性土界面的似摩擦角为sδ ,该界面上的法向应力为sσ ,则刚性区域端部所受应力sp 为

刚性区域与砂性土界面也属于混合边值问题Ⅴ区,也有 1k =- ,得
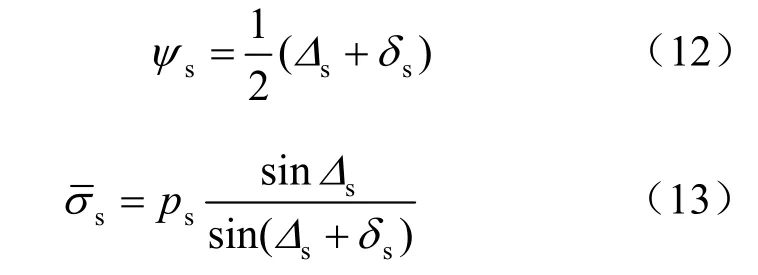
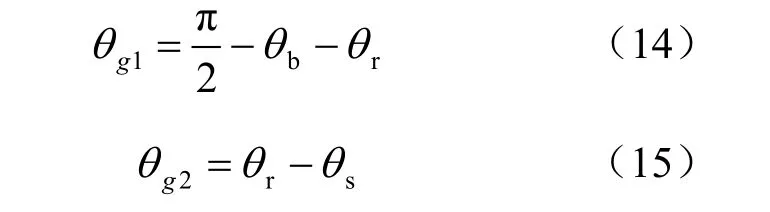
依据Sokolovski 在1965 年提出的理论[23],在柯西边值问题Ⅱ和Ⅳ区有

将式(4)、(6)、(10)、(14)、(16)合并得

将式(4)、(6)、(13)、(14)~(17)合并得

假定肋块土工膜上肋块高度为 Hr,肋块上刚性区域高度为 Hs,且 Hs= βHr;母膜的有效长度和宽度分别为L 和B,肋块长度和宽度分别为l 和b,于是单个肋块的端承阻力 Fb为
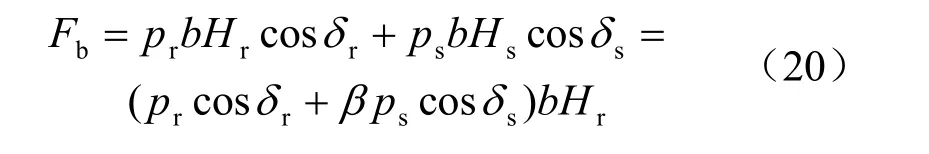
则有单个肋块的端承阻应力为
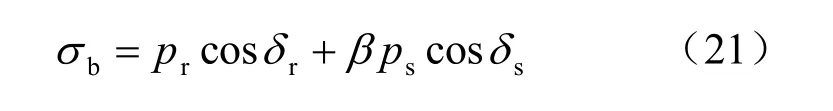
考虑到在直剪试验过程中,与肋块接触的砂性土会有一个被挤密的作用,为此对rp 乘以修正系数λ,于是有
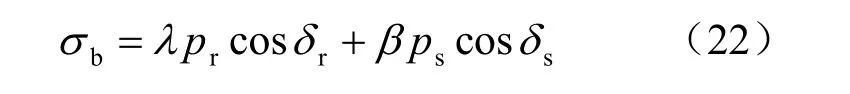
于是块状加肋土工膜与砂性土界面总阻力计算公式为
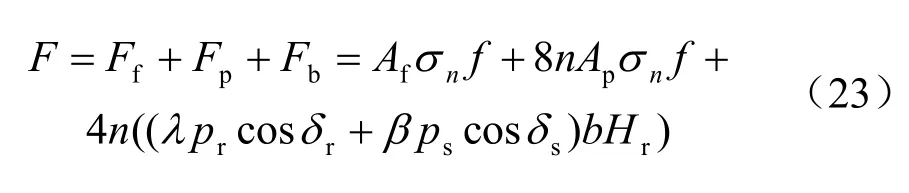
式中: Af= LB(m2); Ap= bHr(m2);n 为肋块排数。
则有块状加肋土工膜与砂性土界面总阻应力为
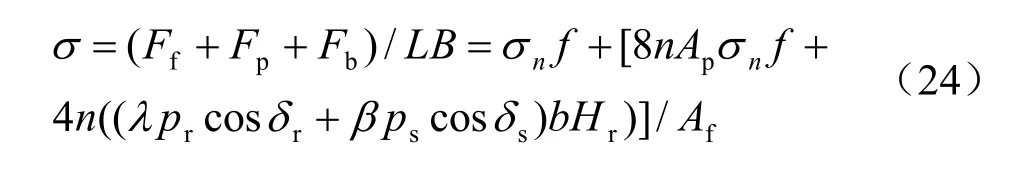
当单个肋块长度达到两肋块间中心距离s 时,这时块状肋块变成条状肋块,侧摩擦力不再发挥作用,于是式(24)为
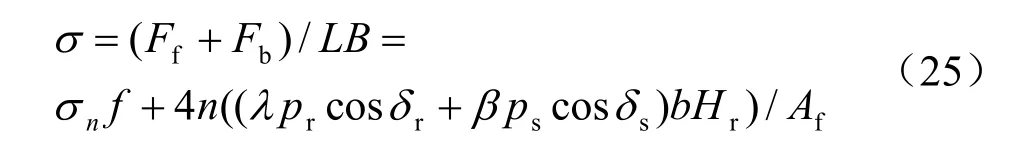
4.2 理论公式的试验验证
本次试验中砂性土的黏聚力 cs=10 kPa,内摩擦角 φs=32.5°,光面土工膜与砂性土界面的摩擦系数f 由直剪试验测得,其在法向应力为50、100、150 、200 kPa 下的摩擦系数分别为0.60、0.53、0.49 和0.48,为使用方便,取不同法向应力下界面摩擦系数的平均值为0.53。
考虑到加肋土工膜上肋块在试验过程中并不会同时达到峰值强度,故对肋块端部应力rp 取修正系数λ=0.95。同时,参考有关文献[9],sr2H H= 。将式(24)、(25)计算得到的界面端阻应力与试验值进行对比,如表2、3 所示。可以看出,界面理论值与试验值表现出相同的规律性,即都随着法向应力的增大而增大。

表2 σ n =100 kPa 界面总阻应力理论值和试验值的对比 Table 2 Interface total resistance comparison of theoretical values and experiment values when σ n =100 kPa
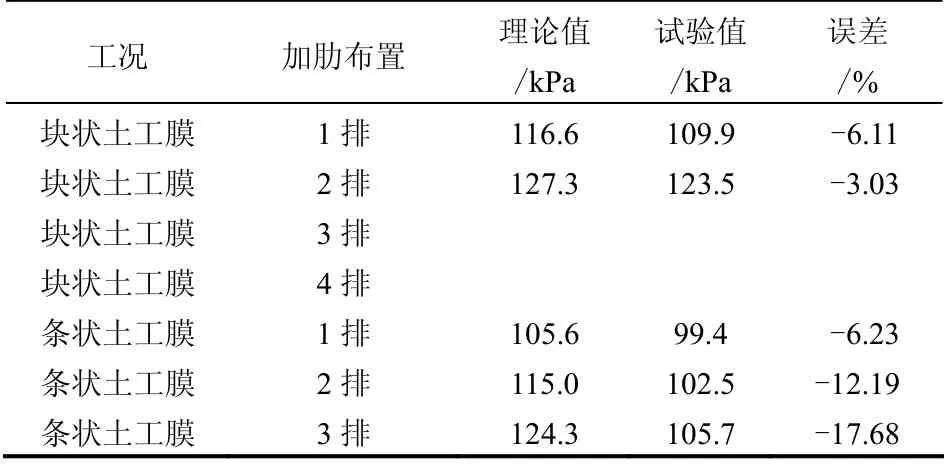
表3 σ n =200 kPa 界面总阻应力理论值和试验值的对比 Table 3 Interface total resistance comparison of theoretical values and experiment values σ n =200 kPa
在试验过程中,加肋土工膜与砂性土界面随着剪切位移的增大而发生相对位移,界面作用将从单一的静摩擦力转为滑动摩擦和肋块与砂性土之间的咬合力。为此,可将加肋土工膜与砂性土界面的直剪试验分为两个阶段:加肋土工膜与砂性土无相对滑移的静摩擦阶段和发生相对位移后滑动摩擦阶段,不同阶段的受力机制也不完全相同。其中,第1 阶段只是界面上的摩擦作用,而在第2 阶段,除了界面的摩擦作用外,肋块端部的端承阻力将逐渐发挥作用。结合理论式(24)、(25),可得界面端承阻力和总阻力的大小以及它们之间的比例关系,如表4。
从表中可知,在低法向应力下双排块状土工膜与砂性土界面端承阻力与界面总阻力的比值为12.5%,随着法向应力的增大,界面端承阻力与最大剪切力的比值逐渐增加,到200 kPa 时界面端承阻力就占16.6%。这说明当法向应力增大时,肋块端承阻力能得到更好地发挥,从而有效地提高了界面的抗剪强度。

表4 端承阻力和界面总阻力比值 Table 4 Ratio of bearing resistance and interface total resistance
5 结 论
(1)加肋土工膜与砂土界面剪应力-位移曲线 基本呈双曲线,试验中肋块间砂土的挤压会影响肋块的受力和变形。
(2)加肋土工膜与砂性土界面总阻力由面摩擦力、侧摩擦力和端承阻力3 部分组成,能有效地描述界面总阻力的力学特性。
(3)肋块端承阻力是提高加肋土工膜与砂性土界面总阻力的原因,尤其在法向应力较高的情况下,肋块端承阻力更能得到充分发挥。
[1] SHEN Zhu-jiang. Limit analysis of soft ground reinforced by geosynthetics[J]. Chinese Journal of Geotechnical Engineering, 1998, 20(4): 82-86.
[2] DIXON N, JONES D R V. Engineering properties of municipal solid waste[J]. Geotextiles and Geomembranes, 2005, 23(3): 205-233.
[3] MITCHELL J K, SEED R B. Kettleman hills waste landfill slope failure I: liner-system properties[J]. Journal of Geotechnical Engineering, 1990, 116(4): 647-668.
[4] PALMEIRA E M, VIANA N L. Effectiveness of geogrids as inclusions in cover soils of slopes of waste disposal areas[J]. Geotextiles and Geomembranes, 2003, 21(5): 317-337.
[5] GIRARD H, FISCHER S, ALONSO E. Problems of friction posed by the use of geomembranes on dam slopes— examples and measurements[J]. Geotextiles and Geomembranes, 1990, 9(2): 129-143.
[6] JEWELL R A, MILLIGAN G W E, SARSBY R W. Interaction between soil and geogrids[C]//Polymer Grid Reinforcement, London: [s. n.], 1984: 18-30.
[7] DYER M R. Observation of the stress distribution in crushed glass with applications to soil reinforcement[D]. Oxford: University of Oxford, 1985.
[8] KOERNER R M, WAYNE M H, CARROLL R G. Analytic behavior of geogrid anchorage[C]//Proceedings of Geosynthetics '89 Conference. San Diego: [s. n.], 1989: 525-536.
[9] IRSYAM M, HRYCIW R D. Friction and passive resistance in soil reinforced by plane ribbed inclusions[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1991, 41(4): 485-498.
[10] JACOB J B, ESTERHUIZEN A M, GEORGE M, et al. Constitutive behavior of geosynthetic interfaces[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2001, 127(10): 834-840.
[11] 高俊丽, 张孟喜, 张文杰. 加肋土工膜与砂性土界面特性研究[J]. 岩土力学, 2011, 32(11): 3225-3230. GAO Jun-li, ZHANG Meng-xi, ZHANG Wen-jie. Interface property between sand and reinforced geomembrane[J]. Rock and Soil Mechanics, 2011, 32(11): 3225-3230.
[12] 高俊丽, 张孟喜. 一种土工合成材料之间及土工合成材料-土之间大型直剪仪: 中国, 200910200536.7[P]. 2009-12-25.
[13] MILLIGAN G W E, TEI K. The pull-out resistance of model soil nails[J]. Soils and Foundations, 1998, 38(2): 179-190.
[14] PALMEIRA E M, VIANA H N L. Effectiveness of geogrids as inclusions in cover soils of slopes of waste disposal areas[J]. Geotextiles and Geomembranes, 2003, 21(5): 317-337.
[15] ZHANG M X, ZHOU H, JAVADI A A, et al. Experimental and theoretical investigation of strength of soil reinforced with multi-layer horizontal-vertical orthogonal elements[J]. Geotextiles and Geomembranes, 2008, 26(1): 1-13.
[16] 张冬霁, 卢廷浩. 一种土与结构接触面模型的建立及其应用[J]. 岩土工程学报, 1998, 20(6): 62-66. ZHANG Dong-ji, LU Ting-hao. Establishment and application of a interface model between soil and structure[J]. Chinese Journal of Geotechnical Engineering, 1998, 20(6): 62-66.
[17] PALMEIRA E M, LIMA N R, MELLO L G R. Interaction between soils and geosynthetic layers in large-scale ramp tests[J]. Geosynthetics International, 2002, 9(2): 149-187.
[18] CHIWAN H, HSIEH H W. Load plate rigidity and scale effects on the frictional behavior of sand/geomembrane interfaces[J]. Geotextiles and Geomembranes, 2003, 21(1): 25-47.
[19] MORACI N, GIOFFRE D. A simple method to evaluate the pullout resistance of extruded geogrids embedded in a compacted granular soil[J]. Geotextiles and Geomembranes, 2006, 24(2): 116-128.
[20] WILSON-FAHMY R F, KOERNER R M, SANSONE L J. Experimental behavior of polymeric geogrids in pullout[J]. Journal of Geotechnical and Geo- environmental Engineering, 1994, 120(4): 661-676.
[21] SIEIRA A C, GERSCOVICH D, SAYAO A. Displacement and load transfer mechanisms of geogrids under pullout condition[J]. Geotextiles and Geomembranes, 2009, 27(4): 241-253.
[22] JEWELL R A. Reinforcement bond capacity[J]. Géotechnique, 1990, 40(3): 513-518.
[23] SOKOLOVSKI V V. Statics of granular media[M]. New York: Pergamon Press, 1965.
