全方向M型心动图中非功能运动的分离和修正
2012-12-31杨秀芝王卫星
杨秀芝 王卫星 林 强
(福州大学物理与信息工程学院,福州 350108)
引言
心脏是人体的重要器官,它的运动与其功能紧密相关。因此在心脏疾病的诊断中,对心脏的运动分析是十分必要的。由于超声诊断具有实时、直观、无损伤、及时获取等特点,为医生对心脏的解剖结构和动态过程的了解提供了全面的信息。这种方法在诊断心脏疾病时具有易于操作、灵活、成本低等特点,所以目前它仍是心脏疾病的重要检查手段之一。
传统的M型超声心动图是通过显示采样线上心脏结构的运动曲线,测量室壁运动的各种参数(如室壁厚度、心室内径、室壁短轴缩短率、射血分数、心血管运动时间等),对心肌功能进行分析。这种检测最大弱点是超声的入射角不一定与运动方向一致,所获得的速度误差较大。解剖 M型(amatomic M-mode,AMM)超声心动图是对原始二维图像的信息进行后处理,从二维图像上可任意调节采样线的位置,获取任意室壁阶段或切面上感兴趣的局部心肌运动曲线。但AMM超声心动图在同一个心动周期的二维图像上只能设置三条取样线,无法获取同一心动周期内所有室壁心肌运动的曲线。福州大学生物医学工程研究所发明的全方向M型心动图系统改进了AMM超声心动图,可以在同一心动周期对不同部位的心肌运动进行任意多条运动曲线的同步成像,能同时记录下心脏内任意结构多个心动周期的 M型超声图像[1-2]。然而由于心脏受到呼吸、血液涌动以及各结构的互相牵动造成的非功能性运动的影响,心脏室壁并不总是沿某条采样线直线运动,初始时刻在这条采样线上的心脏的某个结构,在运动的过程中会脱离这条方向线,或者由于肌肉牵拉等在这条采样线多(少)移动了一段距离,导致重建得到的灰度-时间波形图含有其他结构的运动信息。显然,这样所得到的灰度-时间波形图不能准确反映心脏结构某个部位的功能运动情况。
修正心脏非功能性运动常用运动跟踪、图像配准等方法[3-6]。图像配准常用于匹配一段时间内来自不同或同一患者的医学图像,检测的是图像的相似度,对于含有心室舒缩运动的心脏序列图像效果并不很理想。基于特征的图像跟踪是跟踪图像的整体或部分运动,达到图像匹配的目的。文献[7]采用遗传算法跟踪特征点的运动修正心脏非功能运动,但在心脏B超图像中常常难以找到只含有非功能运动的特征点,因此它的应用范围有限。本研究通过获取B超平面内心脏的平移和心室的偏转修正心脏的非功能性运动,改善获取的心动波形图的准确性。因为B超图像的局限性,仅能提供其平面内的运动信息,因此为了减小心脏偏离B超平面的运动,在采集图像时应要患者尽量屏住呼吸,并且通过对超声探头位置和取向的准确把握减小呼吸造成的心脏抖动和旋转运动,进而提高心脏运动参数测量的精准性。针对心脏短轴B超图像,采用基于心室轮廓线的运动跟踪方法修正心脏非功能性运动。
1 改进的Canny算法
在心脏短轴B超图像中,心腔轮廓的径向变化体现了心脏的功能性舒缩,而轮廓的整体平移和在二维B超平面中的旋转体现了心脏的非功能性运动。目前边界提取算法的改进使得获取心脏心室轮廓成为可能,一个正常人的心动周期大约为0.75~1 s。DICOM标准图像为75帧/s,每一帧的时间间隔约为13 ms,这相对于心脏的运动周期要小得多,因此每帧图像之间具有较强的空间相关性。为此,将室壁轮廓线的提取分为两个阶段:(1)首帧图像室壁轮廓的提取;(2)后续帧室壁轮廓的提取。经过对多种边界提取算法的实验比较,首帧轮廓的提取采用改进的 Canny算法[8-10]并辅以改进的基于径向灰度搜索算法[11],后续帧采用改进的 Canny算法并辅以相邻帧匹配的方法获得左心室短轴轮廓。下面介绍改进的Canny算法。
在Canny算法中,由于二维高斯滤波器可以由两个一维高斯滤波器叠加而成,所以讨论一维高斯滤波器。其数学表达式为

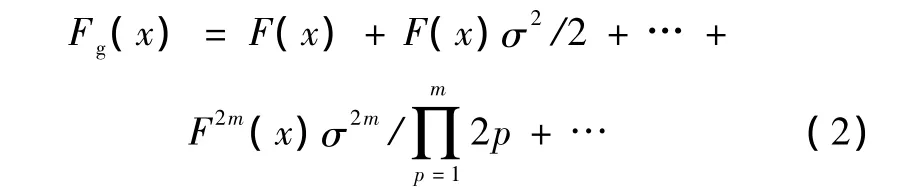
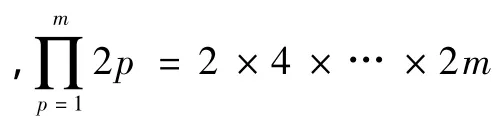
参数σ2决定平滑图像的程度,如果太小,则不能完全消除噪声,而太大则会产生假边缘。解决该矛盾的方法有两种:一种是采用不同的滤波器和不同的平滑参数对图像进行预处理,再进行图像的边缘检测,最后通过分析这一系列结果来合成图像的边缘。另一种是采用Hodson提出的方法。该方法基于图像的不同部分的噪声和边缘类型不同而采用不同的平滑方法。具体如下:
信号F(x)的高斯滤波可表示为。省略高阶导数可近似表达为

定义预处理的误差

所以有σ2(x)=2ε/|F(x)|(5)
采用后一种方法并进行了改进:假设可获得的信号S(x)等于原始信号F(x)加噪声N(x),则有

根据人的视觉系统对平缓部分的噪声和边缘比较敏感,而边缘部分的二阶导数比较大,所以 σ2必须尽量小;平缓部分的二阶导数比较小,所以 σ2必须大,用式(7)代替式(5),有
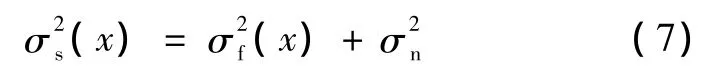
式中,σs(x)是可获得信号的平滑参数,σf(x)是原始信号的平滑参数,σn(x)是噪声的平滑参数。再根据上述结论有

式中,k为比例系数。当x在图像边缘时,F(x)变化很快,所以:(x)≫,即:σ2(x)≅ k/(x)。当x在图像平缓部分:(x)≪,σ2(x)≅ k,可以看出σ2是随x的变化而变化的,因此在二维图像中σ2是随x,y的不同而不同的。根据这一特点,在图像的不同位置采用不同的σ2,从而达到自适应的效果。图1是算法的部分结果,两种方法结合提取心室轮廓可以获得较好的效果。图1中图像来自一位男性心脏左心室短轴B超序列图像,该段B超图像描述了病人3个心动周期的心脏运动情况,周期长度2.5 min,共200帧。所有分析数据都来自这组B超图像。
2 心室轮廓非功能性运动参数的获取
正常的成年人心率约75次/min,平均每—心动周期约占0.8 s。一个心动周期里,心房收缩期占0.1 s,舒张期占0.7 s;而心室收缩期占0.3 s,舒张期占0.5 s。在心脏舒缩的各个期间,心室受到的血液冲击、肌肉牵拉的方向和力量大小都不同,使每一帧的整体位移和在B超照射平面内的偏转也不相同。从轮廓图中可以看出,由于心室的运动、乳头肌的存在以及B超图像的噪声,所得到的轮廓形状不规则,轮廓曲线含有高次谐波分量,称轮廓曲线为类椭圆。随着心脏的舒缩,这个类椭圆的面积大小不断地变化。类椭圆的轴径方向的变化表示了心脏的功能性运动—舒张和收缩,类椭圆的整体位移和偏转则表达了心脏的非功能性运动。傅里叶描述子和质心主轴法都可描述物体的整体运动而忽略细节部分(高频分量),因此采用傅里叶描述子和经典的质心主轴法[12-14]对左心室的轮廓进行了分析和计算,获取其整体运动数据。

图1 心脏左心室室壁轮廓图Fig.1 Contours of left ventricular wall
设图像的横坐标为实轴,纵坐标为虚轴,心室轮廓由N点组成。从心室轮廓上的任一点开始绕轮廓曲线一周,可得到一个一维的复数序列
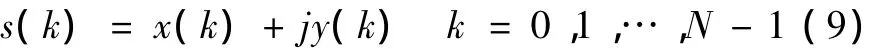
s(k)的离散傅里叶变换为

式中,u为频率,S(u)为s(k)的频谱系数。由傅里叶变换性质可知,傅里叶变换的高频分量对应一些细节,低频分量对应轮廓的总体形状,直流分量对应轮廓所包围区域的质心位置
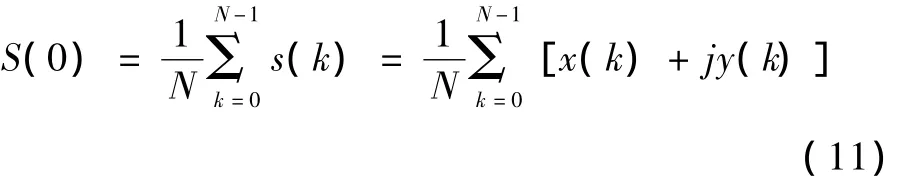
通过傅里叶逆变换,可以由傅里叶系数 S(u)重建轮廓曲线s(k):
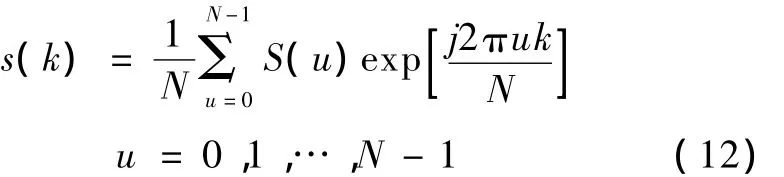
因为傅里叶系数的高频分量对应轮廓细节,低频分量对应轮廓的总体形状,可用对应低频分量的前M个傅里叶系数来近似地重建边界,得到封闭边界的一个近似轮廓(k)
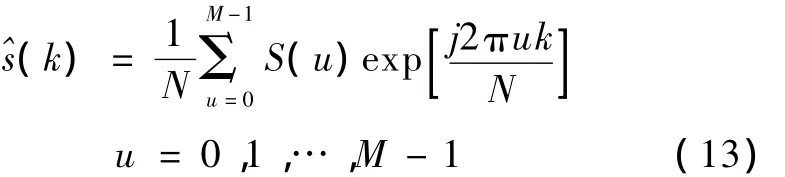
根据轮廓重建实验得知,当 M取40时,^s(k)可以保证既不丢失边界的特征,同时忽略边界的细节和微小波动,这样也恰好减小了心室边缘乳头肌的影响以及轮廓获取过程中的噪声影响和边界误差。
为了消除心室边缘噪声的影响,心室轮廓的质心用重建边界来计算。设前后两帧中的心室轮廓分别为si(k)和si+1(k),则第i帧的质心位置为若轮廓在平面内平移量为(Δx,Δy),则取坐标原点在质心位置,当心脏的舒缩引起心室轮廓大小变化时,轮廓曲线可表示为式中,C为边界放大(缩小)的倍数。它的傅里叶变换:

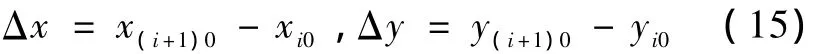

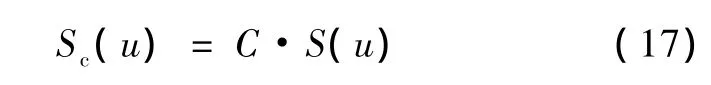
即傅里叶系数也放大C倍,因此由心脏舒缩引起的心室大小变化的影响可以通过傅里叶系数的归一化消除。当选取轮廓起点变化时,设k0为选取不同起点时所引起的序列原点平移量,则:sp(k)的傅里叶变换为:
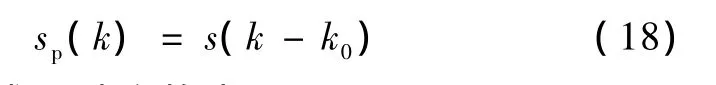
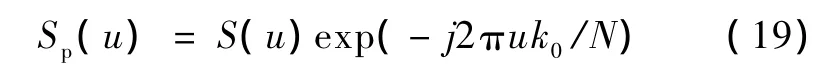
取坐标原点在心室轮廓的质心上,轮廓曲线在空域旋转一个角度θ后可表示为

其傅里叶变换为:
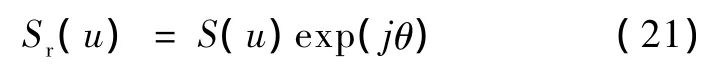
旋转后的傅里叶系数等于原傅里叶系数乘以exp(jθ)。即不同频率成分的傅里叶系数的相位都增加了θ角度,因此可通过傅里叶系数相位的变化规律来检测边界的转动。
去掉直流分量,由式(21)可得前后两帧图像中对应轮廓的前M个傅里叶系数的比值为
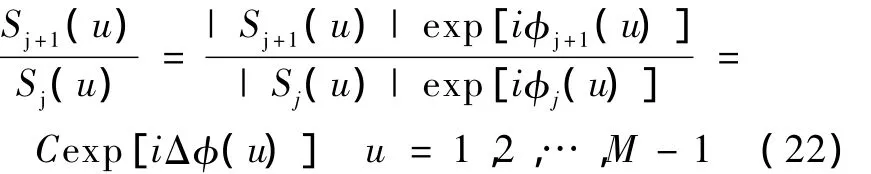
上式中,C为傅立叶系数的幅度比值,反映边界的尺度缩放,而Δφ(u)为不同频率下傅立叶系数的相位变化。由式(19)~(22)可得出前后两帧图像边界的傅立叶系数的相位变化

由式(24)中的直线方程,已知不同频率下傅立叶系数的相位变化,则可以通过Hough变换来确定直线的截距θ和斜率 q。由于u,Δφ(u)空间的一点对应着θ,z参数空间上的一条直线[14]
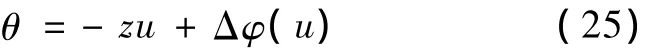
在u,Δφ(u)空间共线的点所对应 θ,z参数空间的直线交于一点,该交点 θ,z值就是所要确定的式(25)中的截距和斜率。求出式(24)中的截距,则可以确定边界曲线的二维平面内的旋转角度[14]。
利用心室轮廓的傅里叶变换的直流分量变化检测轮廓在平面内的平移,利用傅里叶系数的相位变化,再通过Hough变换来检测轮廓的转动。
质心主轴法[15]是根据经典力学物体质量分布的原理,利用检测出的轮廓曲线数据获取心室的质心位置和在二维平面中的主轴方向,通过比对质心的坐标和主轴角度,计算出轮廓的整体运动参数。
3 实验结果及分析
比较数据对应的是一段左心室短轴B超图像的第 11 ~20、22、24、26、28、30、32、38、40、42、44、46、48~59帧,该段B超图像的帧率为80帧/s,患者心率为74次/min,一个心动周期大约对应65帧图像,第11~38帧处于心室收缩期阶段,40~59帧处于心室的舒张期阶段。对于质心位置比较,按照上述方法得到的心脏B超左心室质心位置变化情况见图2。
在图2(b)中,在心室收缩到最小时(约38~44帧),轮廓中心的 y轴坐标明显减小,见图中标志,这是因为此时的心室轮廓下部收缩得很窄(见图1),导致采用直接求轮廓质心的y轴坐标减小(质心位置上移)。采用傅里叶描述子重建边界曲线后,减弱了乳头肌等心内结构的影响,获取的心室轮廓更接近于实际情况,得到的轮廓中心坐标见图2(a)。从图2可看出,在心室的收缩和舒张过程中,心室轮廓的质心做小幅的平移,即心室壁也做相同的平移,虽然每一帧的平移量不大,一般不超过2个像素,这里每一像素等效于0.44 mm,但多帧的累积位移仍会对采样波形图产生明显的影响。因此对心脏平移运动的修正仍是必要的。
关于主轴偏转角度的比较,计算了心室轮廓主轴方向的变化,如表1所示。表1中ya为按照傅里叶描述子方法计算的主轴角度,yb为按照质心主轴法计算的主轴角度。从表1中可以看出,心室收缩和舒张期轮廓主轴的方向略有变化,收缩期主轴角度增大,舒张期主轴角度减小,在心室收缩到最小时,主轴近乎垂直。两种方法计算得到的主轴变化规律和数值大小基本一致。

图2 心脏左心室轮廓中心坐标图。(a)用傅里叶描述子计算;(b)用经典力学原理计算Fig.2 The central coordinates of left ventricular contours.(a)By Fourier descriptors;(b)By principle of classical mechanics

表1 心室轮廓主轴角度列表Tab.1 Angle list of main axis in chamber contour
从上述结果可看出,两种方法都可以分离心室的功能和非功能性运动,得到心室轮廓的非功能性运动参数,基于傅里叶描述子的计算结果更接近于心脏实际运动情况,但主轴质心法计算简单,需要更少的计算量。
4 全方向M型心动图的修正
利用傅里叶描述子算法得到的每帧轮廓曲线的位移和在B超照射平面内的偏转,建立非功能性运动参考模型,指导采样线的位置和方向做等效运动,使所要分析的室壁结构点始终在该方向线上上下运动。

利用这种方法尝试重做了全方向M型心动图。图3显示了采用固定方向线(未去除非功能性运动的方向线)和跟踪采样线(去除了非功能性运动的方向线)时采集的全方向M型心动图。图中给出了4个采样位置时的结果比较,每组图的左侧为采样线的位置,右侧为采样结果。从图3中可以看出经过非功能运动的修正,采样线基本跟踪住了特定结构,如图3(a)所示,能够获得该结构在整个心动周期中的运动情况;获取的全方向M型心动图周期更加明显,波形具有了很强的重复性,如图3中(a)、(b)、(d)所示;获取的边界轮廓清晰,基本不会出现特定点失落和跑偏情况,如图3(b)所示;心动图波形完整,不会丢失采样结构或出现其他组织结构情况,如图3中(b)和(c)所示;心动图波峰比较尖锐,能够反映出心脏受到冲力时的运动情况,而不被整体的大运动所平滑。
5 结论
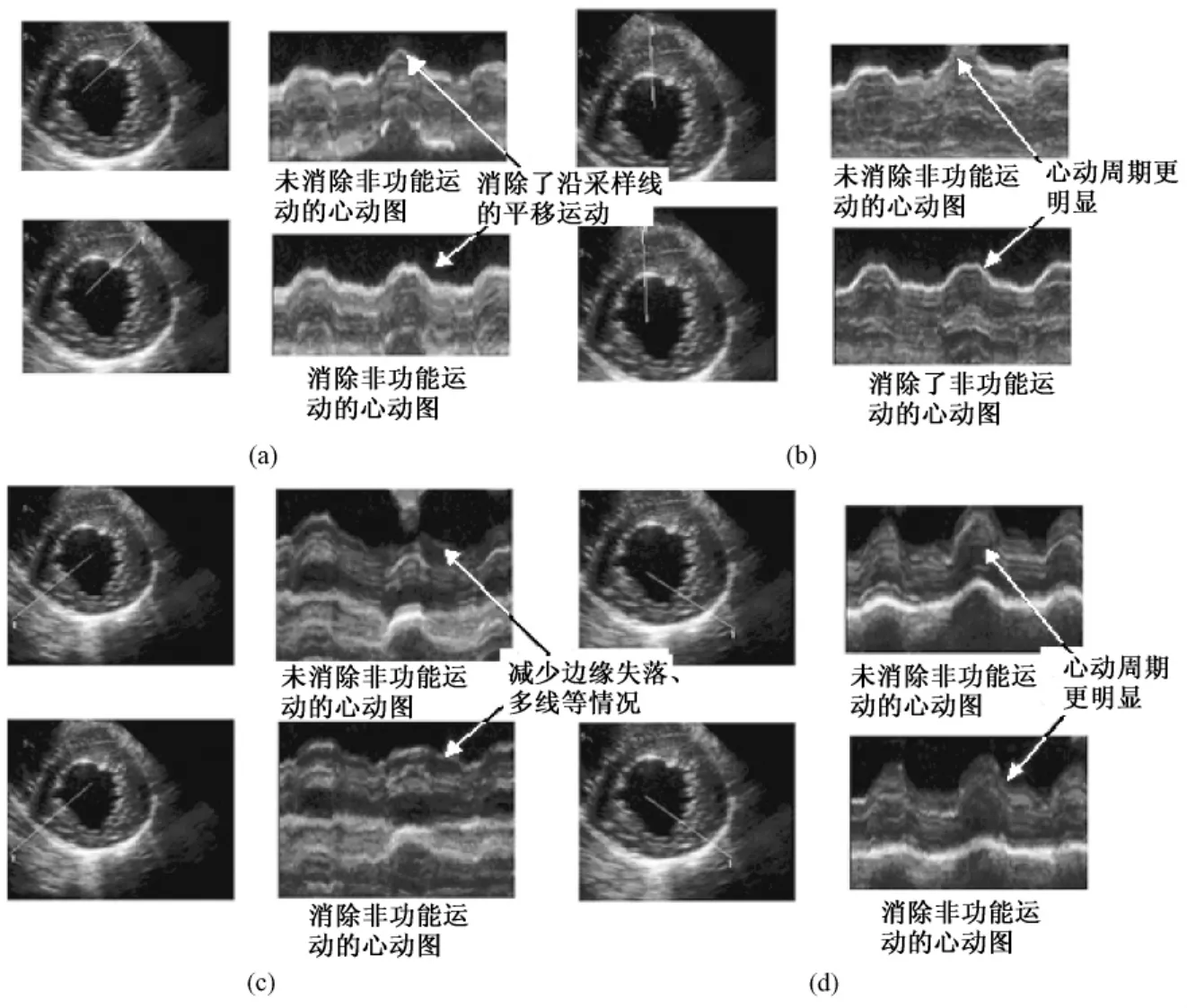
图3 消除非功能性运动前后的M型心动图比较。(a)左上方采样线位置;(b)上方采样线位置;(c)左下方采样线位置;(d)右下方采样线位置Fig.3 Comparison of M-mode echocardiography before and after eliminating non-functional exercise.(a)The site of sampling on the right and upward side;(b)The site of sampling on the upward side;(c)The site of sampling on the left and downward side;(d)The site of sampling on the right and downward side
通过以上分析和实验可以看出,用改进的Canny算法并辅以基于径向灰度搜索算法提取短轴左心室轮廓是可行的,结果令人满意。采用基于心室轮廓线的运动跟踪方法修正心脏非功能性运动是可行的,通过对非功能性运动的修正,采样方向线基本能够跟踪心脏同一结构某个部位在不同时刻的运动,能够较准确地反映心脏结构特定部位的功能性运动。B超平面内的非功能性运动可以通过心室轮廓的整体位移和主轴偏转来表示。采用傅里叶描述子可以较准确地获得一系列图像轮廓曲线的平移和主轴偏转,但计算量较大;采用传统的质心主轴方法也可以快速获得轮廓曲线的平移和偏转,除心室轮廓变形剧烈的图像外(如38~44帧),同样可以改善心动图的准确性。通过对心脏非功能性运动的修正,可以使全方向M型心动波形图更加准确,进而提高心脏运动速度、加速度等功能性动态特征参数的测量准确性。采用本方法对其他患者的心脏短轴B超图像进行的分析实验,可以得到类似的结果。所进行修正的基础建立在心室轮廓的准确提取上,因此高效、快速、准确的提取心室轮廓还将是笔者进一步努力的方向。
[1]Lin Qiang,Wu Wenji,Huang Liqin,et al.An omnidirectional M-mode echocardiography system andits clinical application[J].Computerized Medical Imaging and Graphics,2006,30:333 -338.
[2]林强,石江宏.超声心动图的一种动态信息——全方向M型心动图[J].仪器仪表学报,2005,26(4):437-440.
[3]Guidry DL,Farag AA,Usingactivecontours and fourier descriptors for motion tracking with applications in MRI[C]//Mita D,eds.Proceedings of Image Processing(Volume 2).Kobe:IEEE Signal Processing Society,1999:177-181.
[4]徐牧,王雪松,肖顺平.基于目标轮廓特征的SAR图像目标识别[J].系统工程与电子技术,2006,28(12):1812-1815.
[5]鄢余武,刘进忙.非刚性医学图像的博弈配准方法[J].仪器仪表学报,2010,31(9):2049 -2055.
[6]吴锋,钱宗才,杭洽时.基于轮廓的力矩主轴法在医学图像配准中的应用[J].第四军医大学学报,2001,22(6):567-569.
[7]黄立勤,林强.全方向M型心动图系统精确检测研究[J].仪器仪表学报,2009,30(5):1105 -1109.
[8]张斌,贺赛先.基于Canny算子的边缘提取改善方法[J].红外技术,2006,28(3):165-169.
[9]邵晓芳,孙即祥,王亮亮,等.改进的Canny算法[J].电光与控制,2006,13(6):53 -55.
[10]Canny J.A computational approach to edge detection[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1986,8(6):679 -698.
[11]王同,余建国,王威琪.提取心脏截面图像上内腔的边缘曲线[J].复旦学报(自然科学版),2002,41(2):174 -176,181.
[12]Wang Q,Clarke RJ.Estimation of general 2D motion using Fourier descriptors[J].Vision,Image and Signal Processing,1994,141(2):115-121.
[13]Oirrak AE,Daoudi M,Aboutajdine D.Estimation of general 2D affine motion using Fourier descriptors[J].Pattern Recognition,2002,35(1):223-228.
[14]郑楚君,,杨志勇,何惠玲,等.傅里叶描述子和 Hough变换检测封闭边界运动[J].计算机工程与应用,2005,28:68-69,80.
[15]吴一全,付晓莉.采用角点信息和惯性主轴的车牌倾斜检测与校正方法[J].工程图学学报,2009,6:127-131.
