高频脉冲弱磁场检测技术的研究
2012-12-31陈怡美刘志朋
陈怡美 刘志朋 殷 涛
(中国医学科学院 北 京协和医学院 生 物医学工程研究所,天津 3 00192)
引言
随着检测技术的进步,磁场测量有了很大发展,其应用已深入到工业、农业、国防科技以及生物医学各个领域[1-3]。在生物医学领域,尤其是重复经颅磁刺激(transcranial magnetic stimulation,TMS)的应用中,常涉及的磁场为高频瞬态弱磁场(即频率为0.1~1.0 MHz的时变磁场)。近年来,TMS在脑神经与脑功能研究方向有广泛应用,其所采用的脉冲磁场为微秒级脉冲弱磁场,准确测量磁场强度在TMS应用的安全性方面有着重要意义。
脉冲磁场有多种测量方法,目前广泛应用的磁光效应法适用于强脉冲磁场的测量,其测量精度无法满足弱瞬态磁场的测量[3-5],而基于法拉第电磁感应定律的电磁感应法测量范围宽,灵敏度高,频响不受限,方法简便易实现。目前大多针对脉冲磁场检测技术研究集中在用于原子结构探讨的脉冲强磁场[5]与变电站内存在的纳秒级脉冲弱,磁场[8]等领域,尚未有涉及医疗领域的脉冲磁场测量方法,因此本文基于法拉第电磁感应原理,针对经颅磁刺激等医疗仪器中产生的MHz脉冲弱磁场,研究了0.1~1.0 MHz脉冲磁场,测量及标定的方法和技术。
1 方法与设计
1.1 测量原理
根据法拉第电磁感应定律,把匝数为N,截面积为S的探测线圈放在磁感应强度为B的目标磁场中,保持线圈中心轴线与待测磁场磁力线方向平行,当通过探测线圈的磁通量Ψ发生变化,线圈中就会产生感应电动势[6-8],如图 1所示。采集探测线圈的感应电动势信号ξ或其积分信号Ψ,进行处理和分析就能得出待测磁场的磁感应强度B。基于测量原理,探测线圈应尽量满足以下要求[8,10]:(1)线圈截面积尽可能小,以使线圈所覆盖范围内的磁场能近似均匀,测量结果近似反映线圈所处位置的轴向点磁场值;(2)探测线圈对测量点磁场产生影响应尽可能小;(3)探测线圈平面应垂直于磁场方向。

图1 法拉第电磁感应原理Fig.1 Principle of Faraday's law of induction
1.2 脉冲磁场检测
基于以上原理,研究了脉冲磁场检测方法和技术,其原理如图2所示。该技术包括脉冲磁场的发生、检测及标定。
脉冲磁场的发生部分以AFG3252型函数发生器产生MHz级别的单周期正弦电压为激励信号,经HSA4101功率放大器放大后施加于原发线圈进而激发出脉冲磁场[10-11]。将匝数为N,截面积为 S的探测线圈置于此待测磁场中,使探测线圈平面垂直于磁场方向,则线圈中将会探测到相应的感应电动势。用示波器采集探测线圈中的电压信号,在Matlab 2010b仿真平台上经过一系列信号处理,得出磁场测量值。

图2 脉冲磁场发生与检测过程示意Fig.2 Diagram of pulsed magnetic field generating and detecting
磁场标定装置主要部件(见图3)采用非铁磁性材料有机玻璃加工制成,主要由两个大小各异的工字形线轴和一根与大线轴同心的带刻度游标轴组成。大线轴为原发线轴,用于绕制产生脉冲磁场的线圈,直径D=15.00 cm;小线轴为探测线轴,用于绕制检测脉冲磁场的线圈,D=1.28 cm,探测线轴通过一对顶丝套接固定在游标轴上,可以自由上下滑动,以改变与原发线圈的相对高度;游标轴直径D=1.00 cm,轴上最小刻度为5.0 mm。该装置严格依据法拉第电磁感应定律,保证了测量点位于目标磁场的中心,从而保证了磁场测量值标定的可行性、可靠性和准确性,磁场标定方法将在后文中详细阐述。

图3 脉冲磁场测量装置主要部件Fig.3 Main component of the Pulsed Magnetic Field Measurement device
1.3 脉冲磁场检测数据处理
1.3.1 数据处理方法
将探测线圈产生的感应电动势信号接入示波器通道(CH1),经过示波器采样(采样率为1 G/S)和A/D,D/A转换后,在PC端MATLAB仿真平台上进行信号处理分析,数据处理流程如图4所示。

图4 数据处理流程Fig.4 Data processing Diagram
处理过程由两个部分组成,一是数据预处理,包括滤波和数据截短;二是对预处理数据进行积分并结合线圈参数求解磁感应强度B,数据频谱与滤波分析如图5所示。
1)数据预处理
首先对采集到的数据 Vd进行频谱分析,得到Vd的幅频响应,确定目标磁场信号的频带分布[15-16],依此设计相应的数字滤波器对其进行滤波,去除高频噪声。
图5(a)为原始信号Vd,Vd中心频率为1.0 MHz,如图5(b)所示,采用巴特沃斯IIR滤波器对信号进行低通滤波[9],截止频率fc设置为2.2 MHz。滤波结果如(c)所示,再次对Vf进行幅频分析,结果如(d)所示,滤波后信号的幅频分析中2.2 MHz以上的干扰被完全滤除,中心频率对应幅值从10.32 mV降至10.22 mV,即滤波后信号强度被削弱了约0.8%。
采集数据是探测线圈中感应电动势的全时间段全波形记录,其中除了目标信号之外也记录了外界干扰引入的噪声,滤波之后高频噪声被消除,但低频噪声干扰如基线漂移仍然存在。如图6(a)所示,采集信号基线不为零,这将在每一个积分步长中引入一个基线误差,且该误差随着积分长度而累积增大。因此,对数据进行时间窗截取,取得最小有效积分长度,使基线误差最小化。根据经验令τ~(1±10%)×T,其中T=1/f,τ是时间窗宽,f是激励脉冲频率。图6(a)为数据时间窗设置,将数据波形描绘出来,再根据实际情况设置窗起始点和结束点,截短结果如(b)所示。预处理后得到截短数据Vc。根据电磁感应定律,将 Vc对时间t进行积分,可计算得到通过探测线圈的磁通量Ψ。
2)磁感应强度B计算

图5 数据频谱与滤波分析。(a)原始信号Vd;(b)Vd频谱分析,(上为完整频段曲线图,下为1~16 MHz频段曲线图);(c)滤波信号Vf与原始信号Vd;(d)Vf频谱分析(上为完整频段曲线图,下为1~16 MHz频段曲线图)Fig.5 Data spectrum and filtering analysis.(a)Original signal Vd;(b)Spectrum analysis of Vd(The above is the whole frequency range,the below shows range of 1~16 MHz);(c)Filtered signal Vfand Vd;(d)Spectrum analysis of Vf(The above is the whole frequency range,the below shows range of 1~16 MHz)

图6 数据截短处理。(a)数据时间窗设置;(b)截断后的数据波形Fig.6 Data truncation processing.(a)Data truncation setting up;(b)Waveform of truncated signal
常用的积分方法有模拟积分和数字积分[12-14]。由于模拟积分电路所用的运放、电容、电阻等均为非理想器件,积分结果会受到多种因素影响[13-14]。而数字积分性能稳定,其关键部分在于积分算法,结果的一致性较好。
积分算法的选择遵循以下原则:低采样频率和简单结构。常用的数字积分算法[9]有复化的矩形公式、梯形公式和辛普森公式,等。它们的z传递函数 Hr,Ht,Hs分别为

3种传递函数的幅频及相频分析如图7(a)所示,横坐标为归一化频率,fs为采样频率,Rec、Trap、Simp等3条曲线分别代表复化矩形、梯形、辛普森积分器。由图7(a)知,当实际频率为0~0.01倍fs时,3种积分算法的幅频响应差异并不大;但仅梯形算法和辛普森算法的相频响应有较好的线性一致性,矩形积分法积分结果随实际频率增高而线性衰减。以文中激励参数为例,Vpp=50.0 V,f=1 MHz,采样频率为fs=500 MHz,f/fs=0.002<0.01。分别用3种算法对采集信号进行积分,其结果如图7(b)所示,3条曲线相互重叠,积分结果基本保持一致,与理论分析结果相符。综合考虑算法复杂度和线性相位等因素,采用梯形积分算法,梯形积分公式所产生的误差ES具有阶数O(h2),h为积分步长,取h=1×10-9s,即梯形积分公式产生的误差为 1×10-18量级。
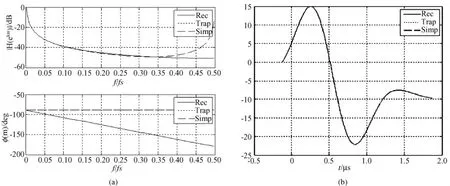
图7 3种积分算法仿真分析。(a)3种传递函数的幅频及相频分析;(b)3种不同积分方式的结果Fig.7 Three integrating algorithms simulation;(a)Frequency Amplitude Domain Analysis and Phase Amplitude Domain Analysis;(b)Integration results of three integrating methods

图8 磁感应强度测量值计算。(a)磁通量Φ(积分后);(b)磁感应强度BFig.8 Calculation of magnetic field.(a)Magnetic Flux Φ(After integration);(b)Magnetic field B
1.3.2 脉冲磁场真实值估计
由于市售常见的磁场探头频响特性无法满足MHz高频脉冲磁场的测量要求,因此本文设计了磁场真实值的估计与标定方法。根据IEEE标准[10],磁场探头在时域有两种标定方法:(1)将已标定磁场探头测量的场强值与待标定磁场探头测量值比对;(2)将待标定磁场探头在能准确计算的参考场中测量,测量值与计算值比对。文中自制磁场检测装置(如图3)用于产生可准确计算的参考场,使用第2种标定方法,即以参考场的计算值作为该磁感应强度真实值的最好估计,并以此标定测量值。
由比奥萨法尔定律可知,载流导线产生磁场的规律可由式(4)描述


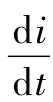
2 实验结果
采用函数发生器AFG3252发生1 MHz正弦脉冲信号,输出信号幅值为0~±5 V,信号经双极性放大器HSA4101进行功率放大,输出电流接入自制磁场检测系统磁场激励线圈,检测线圈上的感应电动势信号用双通道数字示波器TDS2012进行全波记录。
2.1 重复测量实验
令激励电压Vspp=50.0 V,f=1.0 MHz,线圈阻抗与限流电阻阻值之和R=62.1 Ω,激励线圈匝数Ns=5,直径 Ds=15.00 cm,探测线圈匝数 Nd=9,直径Dd=1.28 cm,检测线圈高度Z=0 cm。对此位置磁感应强度进行测量,重复十次,结果如图9所示。
2.2 不同电压激励下磁感应强度测量
改变激励电压Vspp,令f=1.0 MHz,激励线圈匝数Ns=5,直径 Ds=15.00 cm,检测测线圈 Nd=9,直径Dd=1.28 cm,探测线圈高度Z=0 cm。通过双通道示波器同时记录探测线圈感应电动势ξ与限流,Idc是通过示波器直接测量得到的线圈电流值。Bsc较之 Bdc偏小,结合公式可知仿真电流Isc比实际电流Idc偏小,考虑到电路电气特性会受实际环境影响而变化,因此以Bdc作为真实磁感应强度B的估计,对测量结果进行误差分析,相对误差电阻R(61.9 Ω)上电压值 VR随激励变化情况,数据记录如表1。激励电压 Vspp分别为1.0~5.0 V、5.0~10.0 V及10.0~50.0 V时的VR测量值,通过VR可计算线圈电流 Idc,进而得到相应的Bdc作为标准值对探测线圈磁场测量值Bd进行标定,得到对比曲线图如图10所示。由图可见,Vspp<10.0 V时,磁场值与标定值很小,无法直观判断(如图10(b)),但从相对误差曲线图(图10(a))中可以看出相对误差非常大并且出现不稳定跳变,这是因为当激励过小,则线圈电流过小,产生的磁场信号很微弱,几乎被噪声淹没;当 Vspp>10.0 V,测量值与标定值的相对误差依然在2.5%左右,保持较好的测量稳定性和一致性。因此可知此满足系统灵敏度要求的最小激励约为Vmin>10.0 V。知在0.1~1.0 MHz频率范围内系统依然保持较好的一致性和稳定性,相对误差也基本保持稳定,系统具有较好的频响特性。

图9 磁感应强度测量结果。(a)磁感应强度测量值曲线(重复十次);(b)相对误差曲线图Fig.9 Measurement result of magnetic field strength.(a)Magnetic field curve(10 times repetitive measurement);(b)Relative error curves
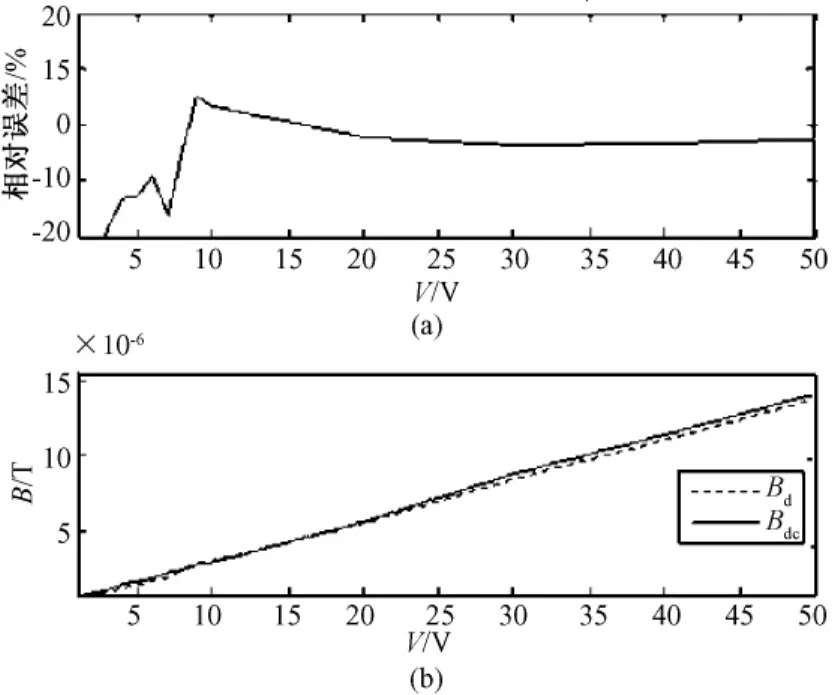
图10 不同激励电压下磁场测量曲线。(a)不同激励电压下磁场测量值与标定值的相对误差曲线;(b)不同激励电压下磁场测量值曲线与标定值曲线图Fig.10 Measured magnetic field curves with different driving voltages.(a)Relative error curve with different driving voltages;(b)Measured magnetic field curve and calibrated magnetic field curve with different driving voltages
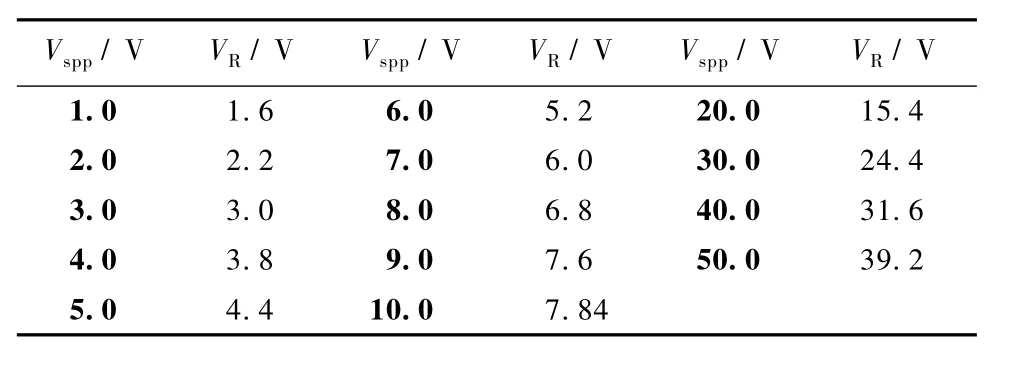
表1 不同电压激励下限流电阻电压值Tab.1 Voltages on the current limit resistance with different driving voltages
2.3 不同频率激励下磁感应强度测量
改变激励频率,令Vspp=50.0 V,激励线圈匝数Ns=5,直径 Ds=15.00 cm,探测线圈匝数 Nd=9,直径Dd=1.28 cm,检测线圈高度 Z=0 cm。分别在0.5、1.0、1.5 MHz等3个频率点进行5次重复测量实验,将测量值Bd取平均值后与标定值 Bdc相比较得出相对误差η,计算结果如表2所示。从表中可
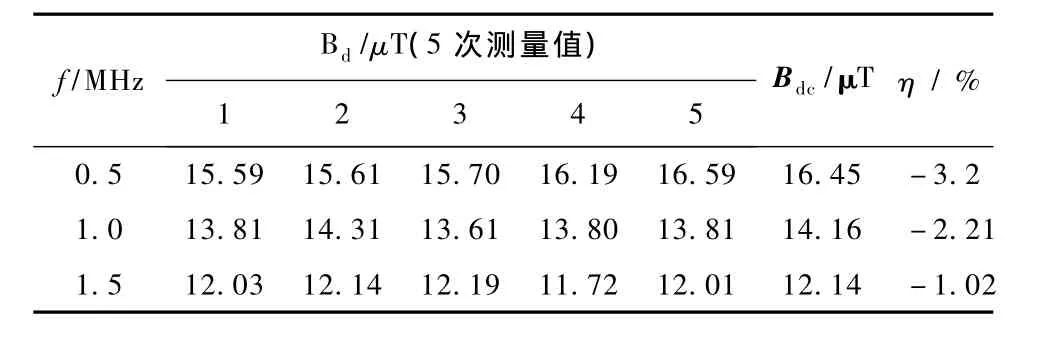
表2 不同频率激励下磁感应强度测量结果Tab.2 Measurement of magnetic field with different driving frequencies
3 讨论
高频弱磁场的检测在生物医学领域占有非常重要的地位,霍尔元件的频率响应无法满足测量要求,因此采用电磁感应法进行磁场测量和标定。
笔者研究了微秒级脉冲弱磁场检测与标定方法,由于信号微弱,对测量准确性要求较高,因此通过自主设计一套磁场标定装置,以准确控制检测线圈与激励线圈间的相对位置与相对高度等实验环境,最终实现了微秒级脉冲弱磁场的测量与标定。实验表明,测量结果基本与真值估计值保持良好一致。
该方法尚有以下几个需要改进的方面:首先,被测信号是窄频带信号,而示波器采集到的是全频段的宽频信号,当采用通用数字滤波器进行滤波时,滤波器会对被测信号进行平滑处理,最终使得信号幅值产生衰减,从文中分析可知最终测量误差与滤波前后信号衰减百分比基本相等,因此设计更加理想的高频响窄带滤波器应做为进一步研究的重点;其次,本文中测量频率范围受到实验设备限制,可测量2 MHz以内的微秒级脉冲弱磁场。实验中所使用的HSA4101功率放大器最大输出电流峰峰值Ipp为2.0 A,最大输出电压峰峰值Vpp为142.0 V,检测系统等效阻抗R为60.0 Ω,因此当激励电压在超过120.0 V时,放大器电流过载不能正常工作。在本研究中Vspp为50.0 V时磁感应强度计算值约为1×10-5量级,容易受到干扰而影响检测结果。同时,功率放大器的频响特性也大大限制了系统工作频率范围,如图11所示。

图11 f=2 MHz时信号波形畸变分析。(a)1 MHz与2 MHz信号放大后的波形比较;(b)2.4 MHz连续正选与脉冲正弦的频谱分析Fig.11 Signal waveform distortion when f=2.0 MHz.(a)Waveform distortion(f=2.0 MHz);(b)Continuous and pulsed sine signal spectrum analysis(f=2.4 MHz)
如图11(a)所示,CH1信号为激励信号频率(f=2 MHz)经功率放大器放大后的直接输出信号,CH2信号为激励信号经放大后加载到激励线圈上,在限流电阻上产生的电压信号,CH1与CH2都产生了信号波形畸变。图(b)中的频谱分析显示,连续正弦信号只有一个频率成分,而单脉冲正弦信号是由多个高次谐波叠加而成,频率成分大约分布在0~12.5 MHz范围内,而采用的双极性放大器HSA4101工作频率范围为DC-10 MHz,频率大于10 MHz信号无法通过,因此最终从功放输出的信号出现了频段缺失,产生波形畸变,因此受仪器频响特性限制,仅对频率小于2 MHz的信号进行研究。
综上所述,本研究建立了一种适用于高频脉冲弱磁场的磁感应强度测量方法,实验证明这种方法能对磁感应强度进行较准确的测量和标定。下一步工作可以对测量方法和测量系统进行更精密的误差分析和频响分析,完成系统的集成化以及数字化,通过计量部门的检验,投入实际应用。
[1]郭中华.时变磁场测量的研究[J].中国科技信息,2008,(13):38-39.
[2]肖保明,王泽忠,卢斌先,等.瞬态弱磁场测量系统的研究[J].高电压技术,2005,31(1):53-54.
[3]Yan Mi,Chen Guoyao,Chun Jiang,et al,A ns-μs Duration,Millitesla,Exponential Decay Pulsed Magnetic Fields Generator for Tumor Treatment[J].IEEE Transactions on Dielectrics and Electrical Insulation,2011,18(4):1111-1118.
[4]石立华,周壁华.EMP磁场传感器的理论与实验研究[J].高电压技术,1996,22(2):9-11.
[5]任晓明,傅正财,孙伟.脉冲磁场测试系统的研究与时域标定[C]//中国电机工程学会高电压专委会2009学术年会论文集.北京:电力工业出版社,2009:435-437.
[6]赵凯华,陈熙谋.电磁学(上)[M].第二版.北京:高等教育出版社,1978:331-397.
[7]屈学民,文峻,张晓军,等.磁感应强度测量仪的研制[J].医疗卫生装备,2008,29(4):22-25.
[8]梁可道,罗宵,米彦,等.纳秒级脉冲磁场传感器的研制[C]//重庆市电机工程学会2008年学术会议论文集.重庆:中国电机学会,2008:330-334.
[9]胡广书.数字信号处理[M].(第2版).北京:清华大学出版社,2003:54-83.
[10]IEEE Std 1309-2005, IEEE Standard for Calibration of Electromagnetic Field Sensors and Probes,Excluding Antennas,from 9kHz to 40GHz[S].
[11]张顺起,刘志朋,靳静娜,等.感应式磁声耦合成像脉冲磁场激励源的设计[J].医疗卫生装备,2010,31(9):18-21.
[12]陈辉,陈卫,李伟.基于Rogowski线圈的数字积分器仿真及研究[J].电力系统保护与控制,2009,37(2):43-45.
[13]彭程程,谷鸣,刘波,等.模拟有源积分器在脉冲磁场测量中的分析与应用[J].核技术,2007,30(9):725-729.
[14]张可畏,王宁,段雄英,等.用于电子式电流互感器的数字积分器[J].中国电机工程学报,2004,24(12):104-107.
[15]翟瑞彩,谢伟松.数值分析(MATLAB版)[M].(第4版).天津:天津大学出版社,2000:230-236.
[16]高成,陈彬,周壁华.小型脉冲磁场屏蔽效能测试设备[J],高电压技术,2002,28(6):27-29.
[17]王震,米东,徐章遂,等.瞬态脉冲磁场频谱分析[J].仪表技术,2010,(9):49-51.
