剑麻纤维强化复合材料计算机仿真研究方法的探索

易春峰 ，王 坤 ，潘 云 ，陈 飞

剑麻纤维强化复合材料计算机仿真研究方法的探索

易春峰1a，王 坤2，潘 云1b，陈 飞1a

(1.中南林业科技大学 a.机电工程学院,b. 交通运输与物流学院, 湖南 长沙 410004；2. 锡根大学，德国 锡根 57068)

提出了一种利用当前主流有限元分析系统ANSYS进行复合材料纤维强化规律仿真研究的方法，借助有限元分析平台对纤维强化的复合材料试件的受力变形过程进行数值模拟，得出不同的纤维强化情况与虚拟试件刚度的相互关系，通过比较计算仿真研究数据与实际实验数据，证明提出的计算机仿真研究方法在复合材料强化规律的研究中是可行的，可以为实际实验指明方向，降低试验和新材料研发的成本。

复合材料；纤维强化；数值模拟；虚拟实验；规律；有限元分析

复合材料纤维强化的形式千变万化，强化后所形成的复合材料的力学性能也各不相同。为了开发新型的纤维强化复合材料，人们必须作大量的试验。传统的方法是先做出不同配方下的大量试件，同一组配方下亦要作出足够多的试件，目的是用统计规律来消除个别试件的特殊性对实验结果的不良影响[1]。这种传统的方法，试验工作量大、工作周期长、成本高，已经与迅猛增长的新材料需求不相适应。随着计算机仿真技术特别是有限元分析方法的日益成熟，完全可以用虚拟试验的方法来研究新的纤维强化复合材料，通过计算机在有限元系统下模拟各种新配方纤维强化复合材料的受力变形过程，达到基本了解该配方的材料特性[2]，对于缩小实际试验的范围，降低试验成本，缩短新材料开发周期具有积极意义。

1 纤维强化复合材料力学性能的计算机模拟研究方法构思

纤维强化复合材料的内部结构比较复杂，不同的零件间在细微的内部结构上都存在一定的差别，要想了解一种配比材料的一般特性，就需要借助于统计学的方法，虚拟试验亦不例外。因此一种配比的纤维强化复合材料也需要做出多个虚拟试件，仿照实际力学性能测试方式进行虚拟力学试验。试验结果的统计平均值作为一般试验值。同一个配方组中每一个虚拟试件的几何模型应该有一定的区别，具体建模时可以借助于随机函数在一定范围内实现，为研究不同配比组分变化对纤维强化复合材料力学性能影响的规律，应该对各种典型配比均进行虚拟实验，并根据试验结果的统计平均值绘制材料力学性能与组分变化关系曲线，从而达到基本了解该类纤维强化复合材料力学特性与组分变化相对关系的目的。

2 纤维强化复合材料力学性能虚拟试验的建模策略

受到当前计算机系统性能的制约，考虑虚拟试件数量庞大的情况，在有限元分析系统(如ANSYS)中对试件进行建模应该优先考虑二维模型，因为三维模型同样计算精度的计算量将较二维模型成几何级数放大，以至于在某些情况下由于计算时间太长而失去现实意义。本例中，实际试件为三维长方体薄片，结构简单，完全可以通过二维剖面的纤维分布规律，使用带厚度的有限元单元对其进行力学性能虚拟研究，只要适当增加样本的数量，就可以通过统计学的方法消除试验结果的误差。具体建模时应该通过有限元分析系统提供的宏指令或其他二次开发工具，通过编程的方法进行自动化建模。下面就矩形截面单一纤维强化复合材料试件在ANSYS中借助APDL开发工具进行自动建模的方法进行探讨。

2.1 模型简化处理

如前所述，首先用二维平面模型替代三维模型，其次在不会显著影响计算结果的情况下，为编程方便，将纤维的随机分层简化为规则的分层排列；将纤维宽度(粗细)的轻微差别，简化为宽度一致。纤维在基体中上下较为随意的相对位置简化为上下均匀分布，且假设试件的上下表面层为基体层，纤维的较为自由的断面形状简化为矩形，如图1所示。达到了模型简化便于编程便于计算的目的。

图1 简化后的二维平面模型Fig.1 Simplified 2D plane model

2.2 基于随机长短纤维和一定纤维密度的虚拟试件几何建模

2.2.1 基本参数计算

为了较为真实的反映实际情况，纤维的长短在一定范围内随机变化且复合正态分布规律。纤维的平均长度就是组分变化的一个主要指标，纤维的密度是组分变化的另一个主要指标。同一层中纤维之间的间隙在一定范围内随机正态分布，平均值可以预先给定，于是可以根据给定密度，决定试件断面的纤维与基体的分布结构[3]，考虑到断面结构如图1所示，几何建模前应该预先根据纤维所占的比例和纤维的粗细尺寸确定纤维的层数和间距。将断面几何模型简化为如图2所示，可推知纤维层数，修正后的纤维断面宽度以及各层的间距计算公式如下:

修正后的纤维断面宽度:

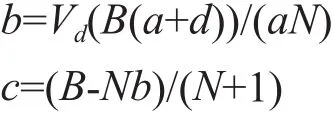
式中：N为纤维层数；nint()为取整函数；Vd为纤维体积密度；a为纤维长均值；b为纤维断面宽度；c为纤维各层间距；d为同一层纤维间距均值；B为试件厚度。

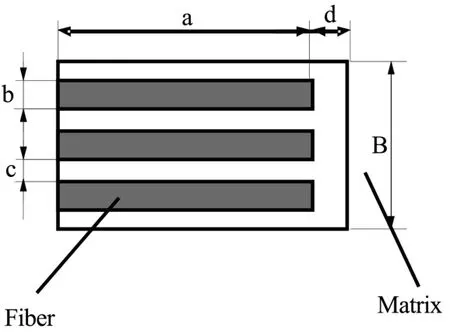
图2 试件断面结构的简化Fig.2 Simplification of specimens section structure

可见由于纤维层数必须是整数，当纤维层数经过取整确定以后，如果纤维体积密度不变，则模型的纤维宽度应有一定调整，考虑到实际试件的纤维层数较多，纤维宽度调整对计算结果的影响可以忽略不计。另一种思路是保持纤维宽度不变，微调纤维体积密度来适应纤维层数的取整。

2.2.2 在ANSYS中自动几何建模方法

利用ANSYS提供的APDL工具编写自动建模宏程序，先利用循环结构分层建立纤维矩形截面，每个纤维的长度用复合正态分布规律的随机函数GDIS(a,q)产生[4]，式中a为纤维长度的均值，q为正态分布函数的标准差。两相邻纤维层纤维排列起始点的横向相对距离，通过随机函数RAND(0,a)按相同的概率生成的0到纤维长度均值a之间的随机数来确定。几何建模的基本思想是先在试件的长度方向上超范围按设定的规则随机铺设纤维矩形截面，达到要求的层数后，作出试件的外轮廓矩形截面（见图3）。

图3 纤维平铺与试件外轮廓Fig.3 Fiber tile and outline of specimen

然后用AINP,all命令对所有相交的矩形面求交得到所有在试件范围内的纤维矩形面如图4所示。再一次作出试件的外轮廓矩形截面作为基体(Matrix)，用AOVLAP,all命令将纤维与基体重叠成一个整体，即纤维与基体共边，如图5所示。注意这里AOVLAP,all以后所生成的新基体的面号，是可能的最小面号，这一点很重要，因为随后要在程序中指定基体和纤维的材料属性，编程时需要知道基体的面号，因此，在前一步求交时后，应该保证最小面号大于2，因此求交后再作的试件外轮廓截面的平面编号为1，这样AOVLAP,all以后所生成的新基体面号必为2(AOVLAP时会先给新生成的基体面一个容许的最小编号2，然后删除先前的外轮廓面号1)。具体实现方法可先在距离试件较远处(在后面求交时不可能交到的地方)先建立两个面，则其编号必为1、2，经过求交后这两个面被删除，留下来的面的编号不会出现1、2。

图4 试件范围内的纤维截面Fig.4 Fiber section within scope of specimen

图5 AOVLAP, all 命令下纤维与基体融为一体并指定材料Fig.5 Fibers and matrix fused together after “AOVLAP,all” command, specified materials with each area

2.3 指定材料属性，划分有限元网格，施加约束与实验载荷

可以先将所有的面指定为纤维材料属性[5]，然后再选择面2指定为基体材料属性[4]，结果如图5所示。下一步通过编程指定有限元网格的尺寸大小(可指定为纤维粗细的一半)，并且选中所有面划分有限元网格。结果如图6所示。按实际试件三点加力弯曲试验情况[6]，编程对虚拟模型施加约束并加载，结果如图7所示。至此，在ANSYS中的虚拟模型建立完毕，只要运行求解器就可得到各节点的位移量和应力值。

3 虚拟模型刚度计算，及内部应力情况分析

要计算虚拟模型的刚度，可根据三点加力弯曲试验的刚度公式来计算，公式如下:

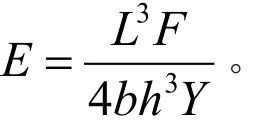
式中：E为弹性模量(kg/mm2)；L为支点间距离(mm)；b为试件的宽度(mm)；h为试件的高度(mm)；F为施加的载荷(kg)；Y为载荷处试件测量点位移(mm)。

图6 右端划分有限元网格后的情况Fig.6 Right end division of specimen after mesh command

图7 对模型施加约束与载荷Fig.7 Applying constraints and load to specimen

计算时的Y值不能简单利用ANSYS的计算值，因为虚拟实验的受力和支撑的指定是按照单个节点来指定的，会造成很大的应力集中和局部变形，如图8所示。这与实际情况不同，计算前应将Y值作修正。

图8 点载荷的局部变形及试件内部应力Fig.8 Local deformation at point load and stress in specimen

式中，Y测点为测量点位移，表示加力方向上的平均位移，Ymin加力点上的位移试件内的应力分布状态也如图8所示。

因这种仿真方法要作大量虚拟试件的仿真计算，所以程序中应该将每次计算的结果按需要写到文本文件中，产生的图像信息也直接以图形文件写入磁盘中。这样程序就可以夜以继日的不中断的进行大量样本的计算。

4 程序总体框架与程序界面的设计

所编写的程序需要频繁地改变各种输入变量，来进行各种材料和纤维长度的尝试，因此好界面有助于提高效率，也为非编程人员使用该工具提供便利。在ANSYS的APDL语言中可以用主程序调用子程序的方式，在主程序中设计输入对话框，来输入各种初始值，并且在主程序中设置循环结构，每循环调用一次子程序，完成一个试件的数据计算和输出。若将子程序写成宏命令形式则主程序调用子程序时最多一次可以传输19个本地变量[7-8]，用ARG1～AR19传递。程序框图如图9和图10所示。

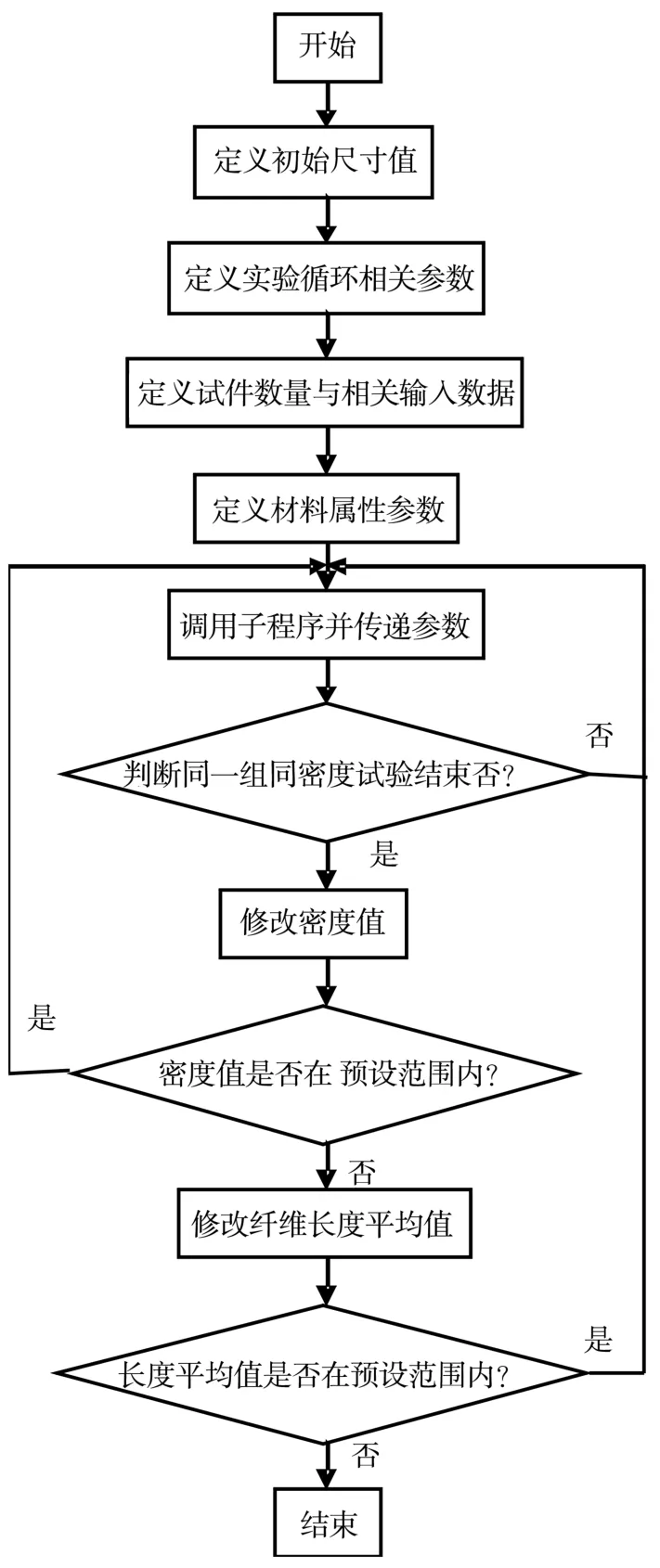
图9 主程序框图Fig.9 Main program diagram of stress in specimen

在主程序中可以用multipro命令，在一个对话框中最多可以输入10个参数值，且可以定义参数的默认值。部分界面如图11所示。

图10 子程序框图Fig.10 Subprogram diagram

图11 部分程序输入界面Fig.11 Some programs input interfaces

5 结果与分析

我们用这一虚拟试验程序按剑麻纤维复合材料试验样本数据:纤维宽度0.05 mm，纤维体积密度0.6，纤维主弹性模量(X方向)7 128 MPa，纤维Y、Z方向弹性模量100 MPa，纤维剪切弹性模量2 060 Mpa，纤维长度正态分布的标准差按纤维长度的10﹪输入，纤维在X方向的平均间距为0.5 mm，试件长度22 mm，试件截面宽度1.6 mm，纤维平均长度变化范围2～16 mm，纤维平均长度步长增量2 mm，支撑宽度18 mm，压力100 N，基体树脂弹性模量500 MPa，及固定纤维长度2 mm，将纤维体积密度在15﹪～75﹪内递增，增量步长为10﹪ ，作了两组虚拟试验来了解同一密度下纤维长短对复合材料刚度的影响规律以及纤维长短相同时纤维的体积密度对复合材料刚度的影响规律[9]，试验的试件弹性模量VS纤维长度曲线和试件弹性模量VS密度的曲线如图12所示，通过将这两组曲线与实际剑麻纤维复合材料试验曲线对比，我们发现，两条曲线大体吻合，证明了我们提出的这种虚拟试验方式基本可行。

图12 虚拟试验数据与实际试验数据对比曲线Fig.12 Comparison between virtual test data and actual test data

照道理，虚拟试件的刚度应大于实际试件的刚度，因为虚拟试件按照理想状态下进行计算，而实际试件的内部会存在气泡、局部脱胶等微缺陷从而降低整体刚度。不过因为我们的虚拟试验方法简化模型时，是用平面模型替代三维实体模型，这样降低了纤维分布均匀性，而使计算刚度比实际刚度有所降低。这两个方面的影响在一定程度上互相抵消，所以最终的数据相差不大。

6 小 结

为提高纤维强化复合材料的试验效率，降低试验费用，我们提出了一种利用有限元分析系统进行复合材料虚拟试验的方法，借助有限元分析平台对纤维强化的复合材料试件的受力变形过程进行数值模拟；为提高虚拟试验效率，我们编制了相关的ANSYS-APDL程序，由主程序进行数据初始化和循环调用，子程序负责自动建立有限元模型并保存分析结果。利用程序虚拟试验了两组试件，得到虚拟试件的刚度VS纤维长度曲线和虚拟试件弹性模量VS密度的曲线，通过与实际曲线对比，曲线基本吻合，证明了这种方法的可行性。

[1] 曹 勇,吴义强,合田公一.甘蔗渣纤维统计强度及纤维增强可降解复合材料拉伸强度的评价[J].高分子材料科学与工程，2008,24(3):90-93.

[2] 金 泉,覃继宁,张 荻,等.颗粒和纤维混杂增强复合材料力学性能的三维有限元模拟[J]. 复合材料学报,2006,23(2):14-20.

[3] 孙爱芳,刘敏珊,董其伍.短切纤维增强复合材料拉伸强度的预测[J].材料研究学报,2008, 22(3):333-336.

[4] 李红周,贾玉玺,姜 伟,等.纤维增强复合材料的细观力学模型以及数值模拟进展[J]. 材料工程,2006,(8):57-60.

[5] 凌启飞,郑 霞,李新功.碱处理对麦秸纤维增强水泥板力学性能的影响[J].中南林业科技大学学报,2012,32(1):157-160.

[6] 王丽雪,尹志娟,刘海鸥.玻璃纤维增强环氧树脂单向复合材料力学性能分析[J].黑龙江工程学院学报：自然科学版，2009,23(3):73-74.

[7] 李 鹏,胡传双,李凯夫.巨尾桉/金属板复合材料层间正应力分布特征的有限元解析[J].中南林业科技大学学报，2010,30(9):107-111.

[8] 博弈创作室.APDL参数化有限元分析技术及其应用实例[M].北京:中国水利水电出版社,2004.

[9] 陈复明,王 戈,李贤军,等.天然纤维织物复合材料制备工艺的模糊评判[J].中南林业科技大学学报,2010,30(11):113-116.

A method of raising sisal fiber reinforced composites performance by using computer simulation

YI Chun-feng1, WANG Kun2, PAN Yun3, CHEN Fei1
(1a.School of Mechanical and Electrical Engineering,b. School of Transportation and Logistics, Central South University of Forestry &Technology, Changsha 410004, Hunan, China; 2. University of Siegen, Siegen 57068, Germany)

A method to research the fiber reinforced material’s reinforcing law was put forward on the basis of a finite element analysis system.The force and the distortion process of composite material were simulated, and the relationship between the reinforce level and the stiffness of different test specimens were studied. It points out that the research method is practicable, through using a finite element analysis to simulate the reinforcing law of fiber reinforced material by computer. This method can be used widely in the new material research economically.

composites；fiber reinforced；computer simulation；virtual test；law；finite element analysis

S795.9

A

1673-923X (2012)07-0128-05

2012-04-18

湖南省科技厅项目（2010FJ3100）

易春峰（1967—），男，江西宜春人，副教授，主要从事CAD/CAE/CAM研究； E-mail：yichunfeng@sina.com

[本文编校：吴 毅]