基于模糊自适应PID的桥式起重机智能防摆控制研究

胡艳丽，刘团结，贾群，沈晓波

（淮南师范学院 电气信息工程学院，安徽 淮南 232038）

基于模糊自适应PID的桥式起重机智能防摆控制研究

胡艳丽，刘团结，贾群，沈晓波

（淮南师范学院 电气信息工程学院，安徽 淮南 232038）

为了消除桥式起重机吊重摆动和实现小车精确定位，提高起重机工作效率，国内外很多学者对防摆控制方法做了大量研究。在建立起重机非线性数学模型的基础上，完成基于模糊自适应PID防摆控制器的设计，其中角度环采用模糊控制器，位置环采用模糊PID控制器。通过与线性二次型最优控制（LQR）仿真结果比较，表明该方法的可行性，其控制过程更加平稳，稳态精度更高，并且当吊重质量和绳长发生改变时，系统仍有较强的鲁棒性。

防摆控制；模糊自适应；线性二次型最优控制；鲁棒性

引言

桥式起重机被广泛应用在电厂、水电站、码头等各个领域，是一种重要的现代化搬运机械。然而其在作业过程中，会受到风力、摩擦等扰动以及负载的提升和小车加减速的影响，会引起吊重的摆动，这不但影响了起重机的工作效率，而且严重时会发生安全生产事故。在传统控制方法中，当吊重摆动时，有些情况下必须通过操作员手动来控制，这就使得工作时间延长，运输过程中的危险性增加。近些年来，很多学者在起重机防摆和小车定位方面做了大量研究[1]：线性二次型最优控制（LQR）、状态反馈、增益调节等等，这些方法都过分依赖于起重机系统的数学模型。

本文针对桥式起重机模型的不确定性和非线性，采用模糊自整定PID技术，设计了一种基于模糊PID的智能防摆控制器[2]，利用小车位置模糊PID控制器和角度模糊控制器分别对小车的位置和吊重的摆角进行控制，模糊控制规则根据起重机操作人员的实际操作经验进行设计。本文对此控制方法在MATLAB/SIMULINK中进行仿真，并和线性二次型最优控制进行比较。

1 桥式起重机防摆控制系统建模

为了对桥式起重机防摆系统进行分析，需要研究影响吊重摆动的因素，因此首先要建立吊重系统数学模型。桥式起重机小车运行系统模型如图1所示。

图1 桥式起重机小车运行系统模型

利用拉格朗日力学进行受力分析[3]，得到起重机系统数学模型为：

其中M为小车质量，m为吊重质量，l为绳长，θ为吊重相对于竖直线的摆角，x为小车位移，F为小车驱动力，g为重力加速度，Fl为钢丝绳起升力。

为了研究方便并考虑到起重机实际工作时的情况，本文先忽略垂直方向时绳长的变化，即有l现Q11对系统的影响较大，而Q33对系统的影响较小。通过对其反复调整，得出当Q11=5000，Q33=110效果最理想，其LQR阶跃响应曲线如图2所示：通常，起重机在安全操作情况下，θ在操作点θ=0附近变化很小，即可以假定 cosθ=1，sin=0，则系统模型可以简化为：

图2 （Q11=5000，Q33=110）时系统阶跃响应曲线

根据对起重机模型的分析，吊重摆动没有直接的驱动器进行控制，抑制吊重摆动归根结底是通过合理控制小车运行，吊重的摆角大小受小车加（减）速度的影响比较大，所以最有效的控制策略就是控制小车驱动电机的转速和加速度。

2 线性二次型最优控制器（LQR）设计与仿真

线性二次型最优控制（LQR）在实际工程设计中有着较广泛的应用，可通过状态反馈实现闭环最优控制。LQR主要研究的问题是：首先建立被控对象数学模型，对其选择一个合适可行的控制规律，能使被控对象按预先设定的要求运行，并且使系统的控制性能达到最优[4]。

根据建模可以得出桥式起重机状态方程式：

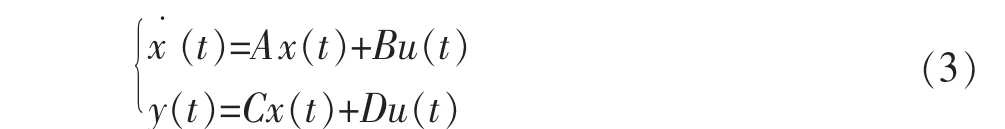
由仿真图2分析，桥式起重机防摆系统通过LQR最优控制器校正之后，小车的位移依然存在着一定的稳态误差，摆角可以在5s左右基本稳定在平衡位置（0rad）附近，但是系统开始时摆动幅度太大（-0.5rad~0.5rad），容易引发安全事故。仿真过程中寻找合适的加权矩阵Q所需要的时间较长，Q11和Q33要反复设定，反复进行试验比较。

3 桥式起重机模糊自整定PID防摆控制器设计与仿真

3.1 模糊自整定PID控制策略

本文采用二维输入三维输出的模糊PID控制器，偏差e和偏差变化率ec作为模糊控制器的输入变量，KP、KI、KD三个语言变量作为输出，实现PID三个参数的在线自调整[5-6]，其控制原理图如图3所示。

使用状态反馈控制率 u（t）=-Kx（t）使得性能指标函数最小。

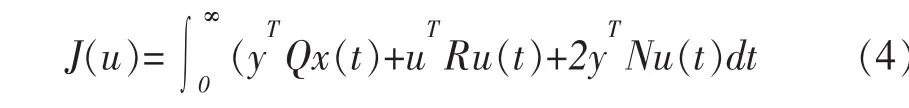
公式中，R为正定对称矩阵，Q为半正定对称矩阵，Q、R分别为x和u的加权矩阵。设计LQR控制器关键是Q的选取，一般Q选取得越大，系统稳定所需的时间越短。

桥式起重机防摆系统是单输入双输出系统，通常直接选择R=1。系统状态变量包括4个量，即小车位移 x，小车速度x·，吊重摆角 θ和吊重角速度θ·，表达式为输出y=[x，θ]。取一组模型参数：

M=2.5kg，m=5kg，l=1m，g=9.8m/s2，μ=0.2，取 R=1，Q=CT*C=diag（1，0，1，0），其中 Q11和 Q33分别代表小车位置和吊重摆角的权重。MATLAB软件提供的求解LQR最优状态的调用指令为：

给系统施加一个阶跃输入，经反复仿真试验，可以发

图3 模糊PID控制原理图

通常定义KP、KI、KD三个参数的调整算式如下：

式中，KP、KI、KD是PID控制器的参数，采用常规方法可以得到 KP、KI、KD的初始参数，设为 KP'，KI'，KD'。在线控制时，通过不断检测系统的偏差e和偏差变化率ec，将其模糊化得到E和EC。

3.2 模糊控制规则

起重机防摆系统包括小车位移和吊重摆角的控制，所以本文采用两个控制器进行控制，即把小车位移x和小车速度x·与吊重摆角θ和摆角速度θ·分离。小车位移控制系统的输出对摆角有很大影响，本文在小车位置环采用模糊PID控制器[7]，角度环采用模糊控制器。这两个控制器之间相互影响，既控制小车使其能停留在期望位置同时又能使吊重保持平衡。

防摆系统中语言变量论域为{-3，-2，-1，0，1，2，3}，输入输出变量的分割数都取 7，即：“正大”（PB）、“正中”（PM）、“正小”（PS）、“零”（ZE）、“负小”（NS）、“负中”（NM）和“负大”（NB）。 本文采用三角形隶属函数，其具有形式简单、对数据信息要求低等优点。根据司机的实际操作经验和仿真试验分别设计了小车位置模糊PID控制器和吊重摆角模糊控制器。 采用“if…then…”形式制定的 KP、KI、KD的模糊控制规则分别如表1，表2，表3所示。吊重摆角模糊控制规则如表4所示。5为l=1m，m=5kg的响应曲线；图6为l=1m，m=9kg的响应曲线；图7为l=1.5m，m=5kg的响应曲线。

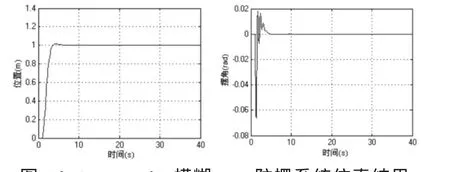
图4 l=1m，m=5kg模糊PID防摆系统仿真结果

图5 l=1m，m=9kg模糊PID防摆系统仿真结果

图6 l=1.5m，m=5kg模糊PID防摆系统仿真结果

3.3 桥式起重机模糊PID防摆系统仿真

完成了模糊PID防摆系统的设计，在SIMULINK环境中运行仿真[8-10]，改变绳长和吊重质量，得到一组模糊PID控制器仿真曲线如下：图

3.4 仿真分析

图4、图5、图6的仿真结果与图2对比可知，采用模糊自适应PID控制器的调节时间 （7s）比LQR方法的时间（5s）稍长，但是采用模糊自适应PID使负载的摆动幅值较小，基本限制在-0.1rad~+0.02rad范围以内，而LQR控制系统的摆动幅值相对来说就大得多，在-0.5rad~+0.5rad之间，这样更加有利于避免安全事故的发生。

4 结束语

本文对桥式起重机小车系统模型进行了研究，针对LQR控制器存在的不足，设计了模糊自适应PID防摆控制器，并在MATLAB环境中对两种控制系统分别进行了仿真。结果表明，模糊自适应PID控制比LQR控制响应速度快，而且起重机防摆系统可以在较小的位置超调下使小车迅速到达目标位置，同时快速消除吊重摆动，因而该方法大大提高了系统的控制性能。图5是把吊重质量增加到9kg时模糊PID控制下的位置和摆角曲线，图6是把绳长增加到1.5m时模糊PID控制下的位置和摆角曲线，和图4进行对比，可以看出在绳长和吊重质量发生改变时，系统仍具有较好的鲁棒性。

[1]张晶.起重机吊重防摇控制研究及控制卡的设计[D].成都：西南交通大学，2008

[2]王晓军，邵惠鹤.基于模糊的桥式起重机的定位和防摆控制研究[J].系统仿真学报，2005，17（4）：936-939

[3]J.J.Rubio-Avila，R.Alcantara-Ramirez，J.Jaimes-Ponce，I.I.Siller-Alcala.Design，construction，and control of a novel tower crane[J].International journal of mathematics and computers in simulation，2007，1（2）：119-126

[4]丁海港，赵继云，张德生.基于LQR的小车-倒摆闭环控制系统研究[J].煤矿机械，2008，29（11）：124-126

[5]崔雅静，杜艳丽，王晓雷.自适应模糊PID控制器的设计[J].控制工程，2008，15：128-130

[6]彭沛夫，林亚平，胡斌，张桂芳.基于遗传因子的自适应蚁群算法最优PID控制[J].电子学报，2006，34（6）：1109-1113

[7]Benhidjeb A，Gissinger G L.Fuzzy control of Overhead Crane Performance Comparisons with Classic Control[J].Control Engineering Practice，1995，3（12）：1687-1696

[8]闻新，周露，李东江等.MATLAB模糊逻辑工具箱的分析与工具[M].北京：科学出版社，2001

[9]王正林，王胜开，陈国顺.MATLAB/Simulink与控制系统仿真[M].北京：电子工业出版社，2005

[10]Nowaeki Z.，owezarz D..On the Roustness of Fuzzy Control of an Overhead rane[J].Proceedings of the IEEE International Symposium on Industrial Electronics，1996：433-437

Research on intelligent anti-Swing control of bridge crane based on Fuzzy self-tuning PID control

HU Yan-li， LIU Tuan-jie， JIA Qun， SHEN Xiao-bo

In order to promptly stop load swing and precisely position the trolley of bridge crane，further to improve the efficiency of cranes，many scholars at home and abroad have done a lot of studies for anti-swing control methods.This paper designs a fuzzy self-tuning PID controller based on nonlinear mathematical model of bridge crane.In the controller， the position loop takes use of fuzzy PID controller，the angle loop takes use of fuzzy controller.The MATLAB simulation shows the feasibility of the method compared with the LQR， the control process is more stable and the control accuracy is higher.Moreover，the system has better robustness and good performance when load mass and rope length change.

anti-swing control;fuzzy self-tuning;LQR;robustness

TP273

A

1009-9530（2012）03-0017-04

2012-02-07

胡艳丽（1982-），女，淮南师范学院电气信息工程学院助教，工学硕士，研究方向为智能控制与信息处理技术。刘团结（1982-），男，助教，工学硕士，研究方向为智能控制。贾群（1976-），男，副教授，博士研究生，研究方向为机电一体化。沈晓波（1982-），男，讲师，工学硕士，研究方向为信号处理与人工智能。