太阳能腔式吸热器自然对流热损的数值研究

龙新峰，于兴鲁，毛青松

（华南理工大学化学与化工学院，广东广州 510640）

太阳能腔式吸热器自然对流热损的数值研究

龙新峰，于兴鲁，毛青松

（华南理工大学化学与化工学院，广东广州 510640）

腔式吸热器是碟式太阳能热发电系统的一个重要组成部分，它的性能优劣直接影响到整个发电系统的效率。重点分析了腔式吸热器的自然对流热损，建立了6种典型腔式吸热器的二维模型，选用FLUENT6．3计算了在开口直径为10 cm，壁温为400℃，倾角α＝0°条件下的6种腔式吸热器的内部自然对流热损失。计算和比较发现，球形吸热器的内部对流热损比其他5种吸热器平均低10%。通过计算球形吸热器在不同Aw／Al（内表面积／开口面积）和不同倾角下的对流热损大小，发现球形吸热器的对流热损随倾角的增大而显著减小，在α＝0°（开口朝侧面）时最大，α＝90°（开口垂直向下）时最小；计算得到球形吸热器的最佳Aw／Al值为8～10。

太阳能热发电；腔式吸热器；自然对流；热损

随着全球一次性能源的不断消耗，太阳能作为一种清洁、可再生能源受到人们越来越多的关注。太阳能碟式热发电系统因其具有热转化率高、机动性好和投资小等优点而被认为是光－热－电发电系统的理想途径之一［1－2］。实际应用中的碟式聚光器受工艺条件和操作误差的影响，如抛物面不规则、不光滑及轨道跟踪的偏差等，会使反射光线偏离焦点，导致实际得到的是焦平面而非焦点。为收集焦平面处的高密度太阳光，需要在焦平面处放置一种开口的腔式吸热器。腔式吸热器开口的大小由焦平面的大小决定，而腔式吸热器的开口大小、腔体尺寸和形状对它的表面换热效果有很大的影响，最终会影响整个吸热器的性能。

腔式吸热器的热损主要由4部分组成：反射热损、辐射热损、对流热损和导热热损。在4种热损中，吸热器的对流热损受几何结构、腔体倾角的影响最大，而且对流热损是非常复杂的一种，它对整个吸热器的性能起了重要影响［3］。大量研究人员对腔式吸热器的内部自然对流进行过理论和实验上的研究。文献［4］通过实验获得了一种梯形腔式吸热器的内部对流热损，并用CFD软件计算了该腔式吸热器的对流热损；文献［5］计算了方腔吸热器在不同倾角和不同长宽比下的对流热损大小；文献［6］用实验的方法测得一种圆柱形腔式吸热器在不同倾角下的内部对流热损大小；文献［7］利用商业软件FLUENT计算和比较了球形、半球形和改进半球形3种腔式吸热器的对流热损大小，求得一种改进半球形吸热器对流传热的Nusselt关联式。

但很少有研究人员对不同几何结构的腔式吸热器进行定量的数值计算和比较。笔者重点通过FLUENT6．3模拟软件，近似计算和比较几种不同结构的腔式吸热器在二维情况下的对流热损大小，研究Aw／Al以及腔体倾角对球形吸热器对流热损的影响。

1 物理数学模型

1．1 物理模型

腔式吸热器的形状有很多种，图1给出了6种典型腔式吸热器的结构图，6种吸热器均为轴对称模型。以球形吸热器为例，其内部传热情况如图2所示，太阳光经聚光碟聚集成高密度太阳光经腔口进入腔体，腔体内壁被加热温度升高，大部分热量通过腔体内壁的导热管导出被利用，一部分热量通过腔口和壁面损失掉。腔式吸热器的热损主要由4部分组成：通过腔口的反射光损失，通过腔口的对流热损失，通过腔口的热辐射损失，通过壁面的导热损失。要研究吸热器的热损需要综合考虑以上4种热损的影响。影响热损的各个因素之间相互影响和制约，较小的开口直径可以减少反射、辐射和对流热损失，但它受到制造工艺、焦平面大小的影响，不能过小，需要综合考虑。反射热损主要由开口直径决定，腔体形状对反射的影响较弱，而对自然对流传热影响较强［3］。空气可被认为是辐射非参与性介质，所以反射和辐射传热几乎不影响对流传热。如果外壁保温层性能良好，则导热损失可以降到很低。因此此次计算不考虑反射和辐射传热，同时假设壁面绝热，单独分析腔式吸热器的对流热损。

图1 几种典型腔式吸热器Fig．1 Several typical cavity receivers

在一天之中太阳光的辐射强度受时间及云层等遮挡物的影响，辐射强度波动很大。为使出口流体温度稳定，在太阳辐射强度大时，要增加导热管中导热介质的流量；太阳辐射强度小时，要减小导热介质流量。通过调节导热介质流量，也可以使腔式吸热器的内壁温度趋于稳定。

为分析腔式吸热器自然对流热损的大小，忽略风的影响，以开口直径均为10 cm的上述6种吸热器为研究对象。因腔体内壁采用导热性良好的金属材料，所以内壁温度比较均匀，可假设内壁温度恒定为400℃，壁面绝热且壁厚均为零，通过模拟软件FLUENT6．3来计算和分析腔式吸热器的形状、内表面积与开口面积之比以及倾角对自然对流换热的影响。

1．2 数学模型

1．2．1 控制方程

腔体内自然对流的模拟计算主要基于连续性方程、动量方程、能量方程的平衡，这些方程可以表示如下［8］。

连续性方程：Δ

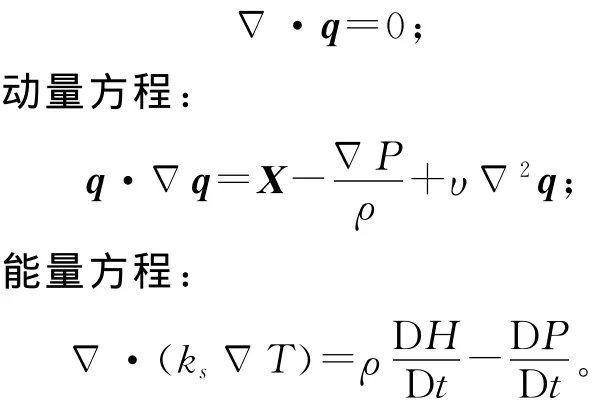
其中：q为极坐标（r，θ，Ф）下的速度向量；Δ为拉普拉斯算子；X为单位体积作用力；P为压力；T为空气温度；ρ为空气密度；υ为空气运动黏度；ks为空气热传导率；D为全微分；H为空气的单位体积焓；t为时间。1．2．2 数值计算的条件设置

采用FLUENT6．3的压力基求解器进行二维稳态计算，选用SIMPLE算法求解速度压力方程，对流扩散项采用一阶迎风格式。设定空气流动状态为层流，空气介质的密度采用Boussinesq近似，空气物性以壁面和空气的平均温度作为基准，内壁面温度设定为恒温400℃，外壁面绝热，外围空气边界条件为P＝Patm的压力入口。连续性方程及x和y方向的速度残差设定为10－3，能量方程的残差设定为10－8。

1．2．3 网格划分

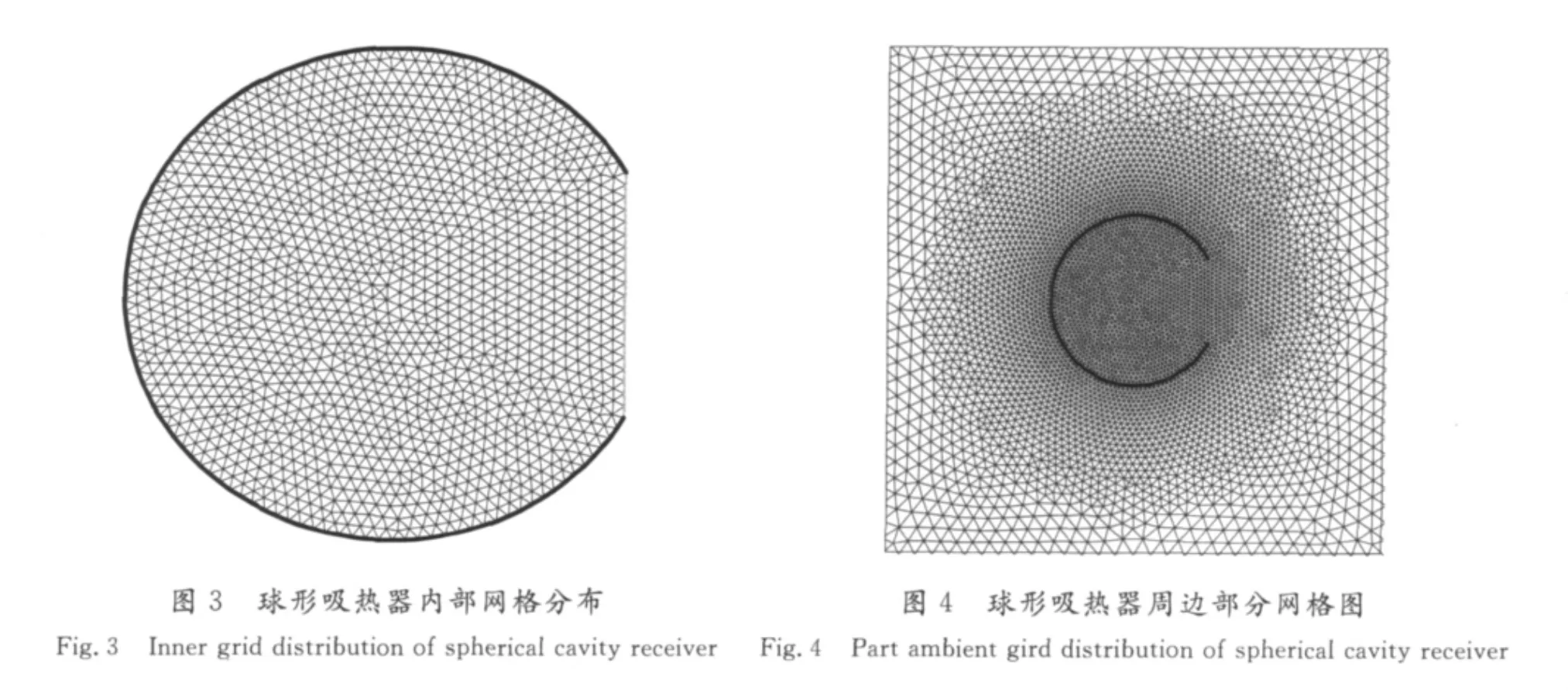
以球形吸热器为例，球体内的网格采用三角形网格进行划分。图3为球形吸热器的内部网格图。在球体外建立一个足够大的流场区域，使外边界的大小不影响空气的流动和换热。球体外的流场区域面积为内流场区域面积的15倍。图4为球体及其周围流场的部分网格，整个计算区域共划分为39 378个单元，其余5种形状的吸热器采用类似的方式划分网格，在近壁面处进行了网格局部加密。

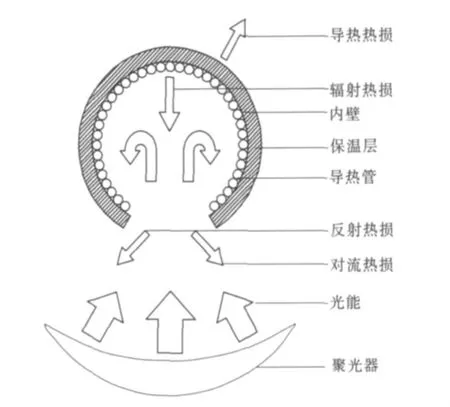
图2 球形吸热器内部传热Fig．2 Heat transfer in spherical cavity receiver

2 结果与分析

2．1 形状对吸热器对流传热的影响

图5所示为6种典型的吸热器在壁温为400℃，开口直径为10 cm，倾角为0°时的温度云图。由图5可以清晰地看到吸热器内部空气被加热的效果，圆柱形、圆锥形和椭球形吸热器内壁面处形成一层薄的热气流，而复合圆锥形、缩口圆锥形和球形吸热器内部形成明显的空气滞留区，滞留区空气的温度高于其他区域。

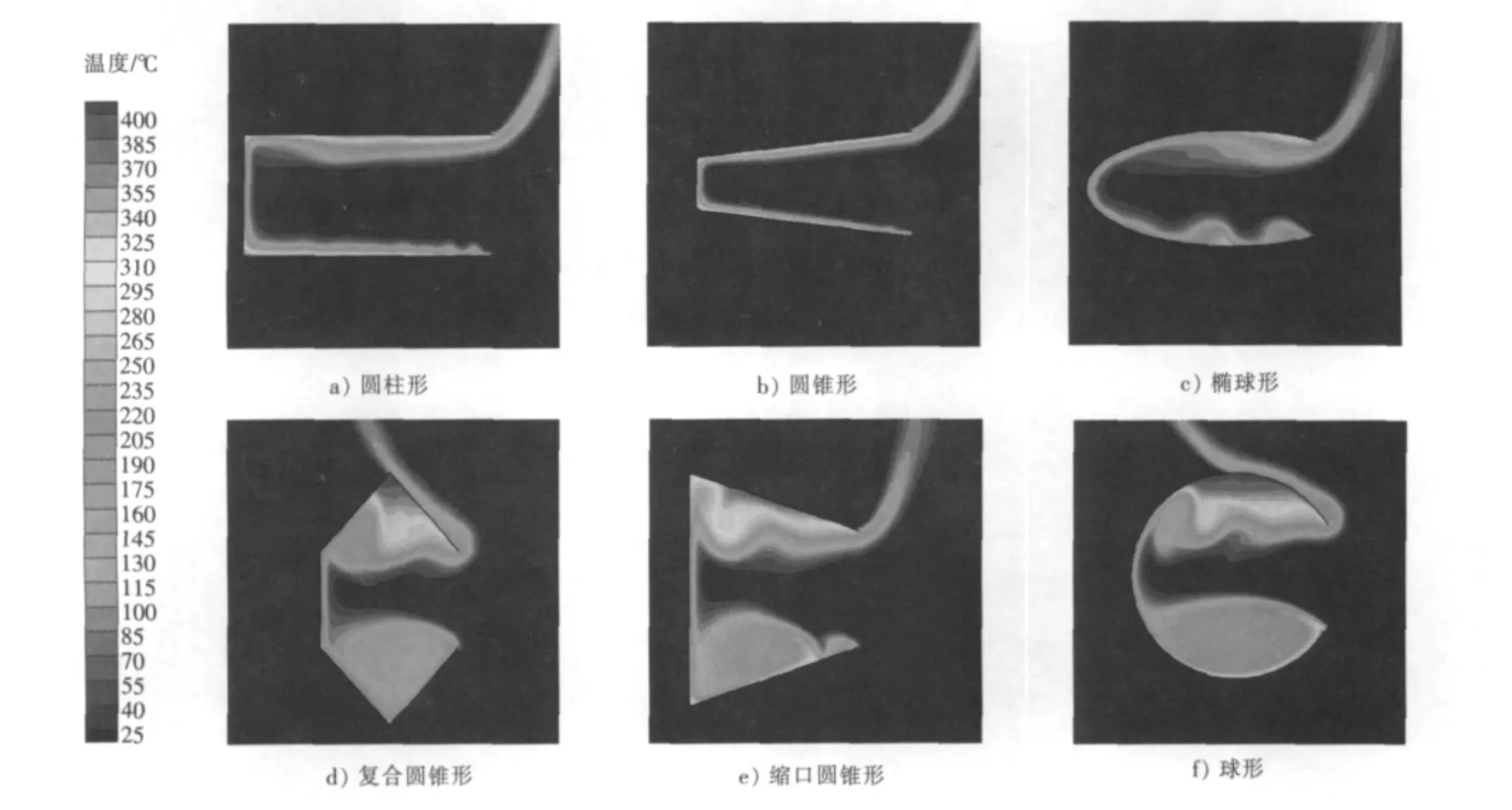
图5 壁温为400℃时不同吸热器的温度云图Fig．5 Temperature contours at 400℃of different cavity receivers

表1给出了FLUENT6．3中计算区域的厚度为0．2 m时6种吸热器的热量计算结果，所有计算结果均满足结果收敛且总质量流量偏差小于10－6kg／s，总能量流量偏差小于0．01 W。由表1可知：6种吸热器中椭球形吸热器自然对流热损最大，比其他5种吸热器平均高出21%，其他5种吸热器的热通量比较接近；从内壁平均热流密度来看，球形吸热器略小于其他吸热器，比其他4种吸热器低10%。表1数据为二维模拟所得，实体为三维结构，在相同开口直径的二维尺寸下，三维球形吸热器相对其他4种吸热器具有更大的表面积，有利于在内表面布设更大面积的导热管道，提高导热面积。

表1 不同腔式吸热器的模拟结果数据Tab．1 Value of different cavity receivers

综合考虑总对流换热量和内表面积的关系可以发现，在这6种典型的吸热器中，球形吸热器的内部自然对流单位面积热损率最小。这主要由球体的结构决定。球体能形成更封闭的区间，形成滞留区，有效减弱了自然对流的强度，而且相对封闭的区间可以减弱自然风的影响，减弱自然风引起的强制对流热损。

2．2 内表面积与开口面积之比（开口比）对球形吸热器的影响

为研究开口比对球形吸热器的影响，对球体直径为30 cm，开口比分别为2，4，6，8，10，12的6种球形吸热器进行二维模拟计算，6种球形吸热器的内壁面温度均设定为400℃，倾角均为0°，采用相同的计算模型、网格类型和网格密度进行计算。

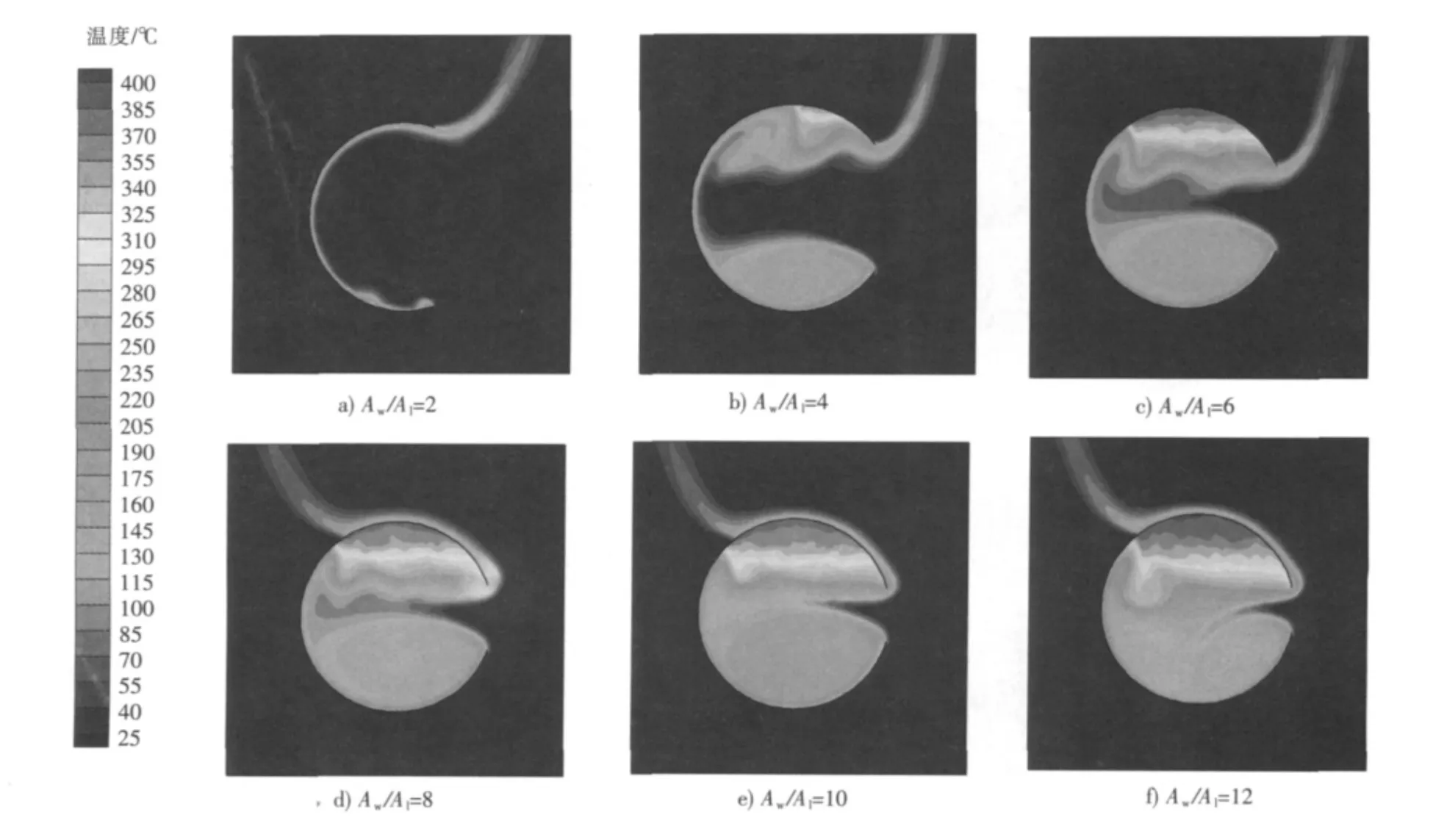
图6 壁温400℃时不同开口比A w／A l的球形吸热器的温度云图Fig．6 Temperature contours at 400℃of spherical cavity receivers with different A w／A l

图6是壁温400℃时不同开口比（Aw／Al）下球形吸热器的温度云图。腔体内空气的高温区出现在球体顶部，且随Aw／A1的增大，高温区面积增大，底部和顶部空气滞留区域面积增大，减弱了自然对流传热。图7给出400℃时球形吸热器的对流换热量随倾角和开口比的变化曲线。由图7可以看出：当2＜Aw／Al＜10时，球形吸热器的对流换热量随Aw／Al增大减小明显；当Aw／Al＞10时，在倾斜角为0°和30°时对流换热量随Aw／Al增大反而升高；在倾角为60°和90°时对流换热量基本不随Aw／Al变化。由此可见，Aw／Al＝10是球形吸热器对流热损的临界点。实际应用中，受到焦平面大小的限制，吸热器的开口不能过小，而较大的开口又会增加对流热损。因此，当球形吸热器的Aw／Al为8～10时，球形吸热器既能满足适当的开口面积，又能保证较小的对流热损。这与REDDY等在研究中得到的结果基本一致［9］。

2．3 倾角对球形吸热器的影响

由图7可知：球形吸热器的对流换热量随倾角显著变化，吸热器由α＝0°增加到α＝90°时，球形吸热器的对流换热量急剧减小，α＝0°时最大，α＝90°时最小，对流换热量接近于零。图8给出了Aw／Al＝8的球形吸热器在不同倾角下的温度云图。由图8可知：随倾角α的增大，球形吸热器内部的滞留区面积显著增大，球体顶部的高温区面积亦显著增大。这是因为在重力作用下，热空气由于密度小，因而上升至球体顶部，在顶部形成高温区。当α增至90°时，热空气基本充满整个球体，使球体内部温差最小，密度差最小，内部自然对流减弱到最小，只在开口处存在微弱对流，所以对流热损最小。

3 结 论

1）通过FLUENT6．3软件模拟6种不同腔式吸热器在相同的开口直径、相同壁温条件下的内部自然对流热损，发现球形吸热器相对其他腔式吸热器具有更小的内部对流热损。

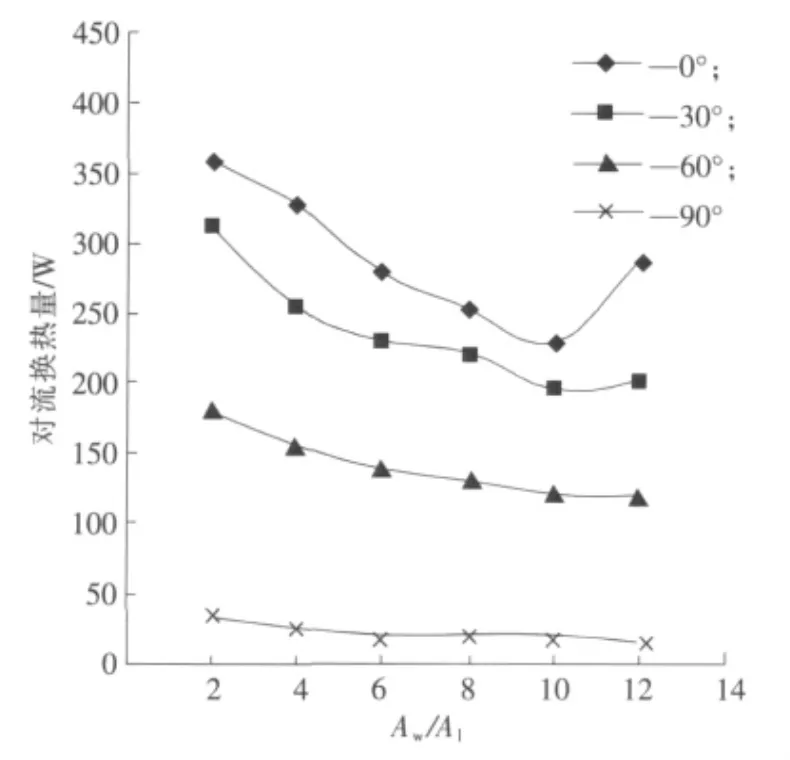
图7 400℃时不同开口比在不同倾角下对应的对流热损Fig．7 Variation of convective heat loss with different A w／A l at 400℃for different inclination

2）对球形吸热器，在不同开口比和不同倾角下模拟其内部温度场分布，计算对流热损。发现对流热损随倾角的增大急剧减小，在开口朝侧面时最大，开口垂直向下时达到最小。通过比较不同的开口比与吸热器对流热损的大小关系，找出球形吸热器的最佳Aw／Al值范围为8～10。由于本文中未考虑辐射热损对吸热器热性能的影响，所以不能给出Aw／Al的具体值。

3）分析了腔式吸热器内自然对流热损的大小，对吸热器的设计有一定指导作用，但计算过程中对模型进行了适当简化，所得结果必然存在一定误差。综合考虑腔式吸热器4种不同热损，可作为未来高热效率腔式吸热器设计中的重要因素。

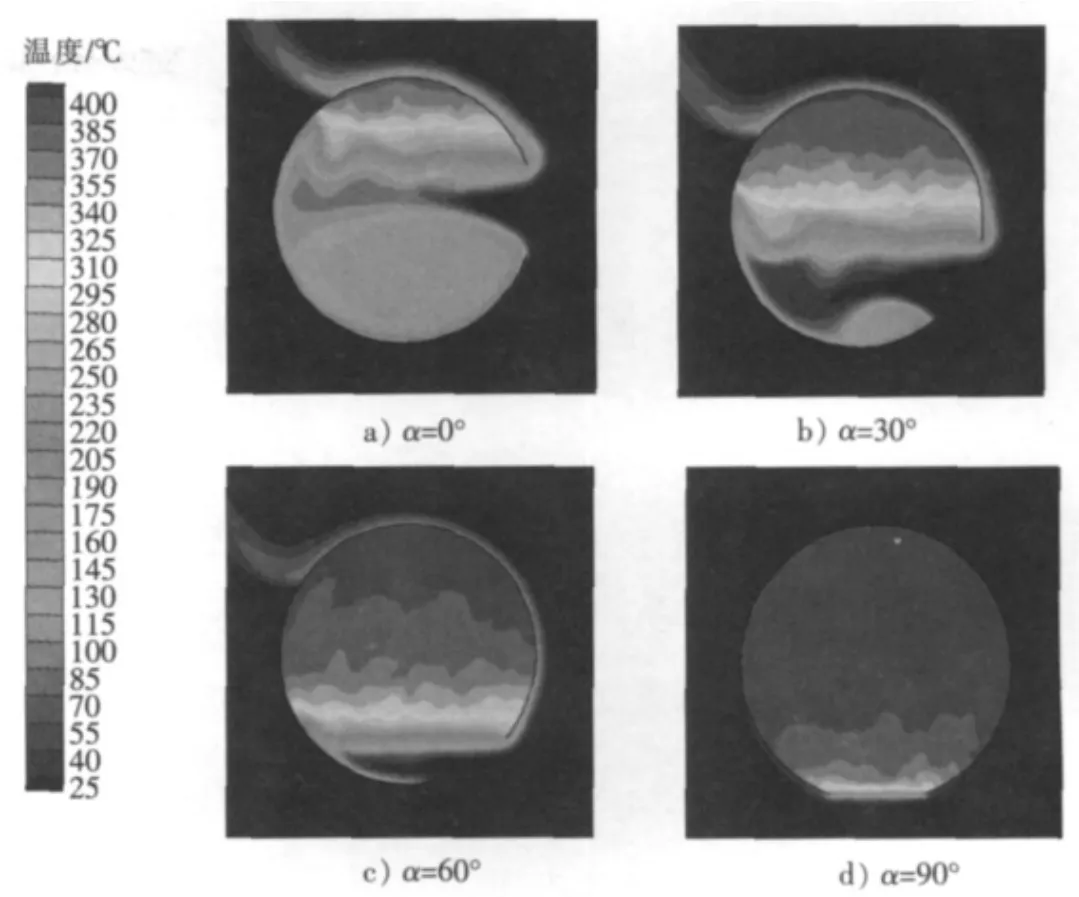
图8 壁温400℃时球形吸热器在不同倾角下的温度云图Fig．8 Temperature contours at 400℃for different inclination of spherical cavity receiver

［1］ ZHANG Chun－ping，LIU Zhi－gang，ZHAO Yao－hua，et al．Thermal performance analysis of cavity receiver for the dish solar energy thermoelectric system［J］．J University of Shanghai for Science and Technology，2004，26（4）：294－297．

［2］ STONE K W，LOPEZ C W，MCALISTER R E．Economic performance of the SCE stirling dish［J］．Energy Engineering，1995，117（8）：210－214．

［3］ LIU Zhi－gang，ZHANG Chun－ping，ZHAO Yao－hua，et al．The design and experiments of a new cavity absorber［J］．Acta Energiae Solaris Sinica，2005，26（3）：332－336．

［4］ REYNOLDS D J，JANCE M J，BEHNIA M，et al．An experimental and computational study of the heat loss characteristics of a trapezoidal cavity absorber［J］．Solar Energy，2004，76：229－234．

［5］ MUFTUOGLU A，BILGEN E．Heat transfer in inclined rectangular receivers for concentrated solar radiation［J］．International Communications in Heat and Mass Transfer，2008，35：551－556．

［6］ PRAKASH M，KEDATE S B，NAYAK J K．Investigations on heat losses from a solar cavity receiver［J］．Solar Energy，2009，83：157－170．

［7］ SENDHIL N K，REDDY K S．Comparison of receivers for solar dish collector system［J］．Energy Conversion and Management，2008，49：812－819．

［8］ SENDHIL N K，REDDY K S．Numerical investigation of natural convection heat loss in modified cavity receiver for fuzzy focal solar dish concentrator［J］．Solar Energy，2007，81：846－855．

［9］ REDDY K S，KUMAR N S．An improved model for natrual convection heat loss from modifed cavity receiver of solar dish concentrator［J］．Solar Energy，2009，83：1 884－1 892．

［10］ SENDHIL N K．REDDY K S．Compraison of receivers for solar dish collector system［J］．Energy Conversiom and Management，2008，49：812－819．

［11］ 侯欣宾，崔海亭．高温相变蓄热在空间太阳能热动力发电系统的应用［J］．河北科技大学学报（Journal of Hebei University of Science and Technology），2001，22（2）：1－3．

［12］ 崔海亭，袁修干，邢玉明．高温固液相变吸热器研究现状与发展［J］．河北科技大学学报（Journal of Hebei University of Science and Technology），2003，24（1）：6－9．

Numerical investigation of natural convection heat loss in solar cavity receiver

LONG Xin－feng，YU Xing－lu，MAO Qing－song
（School of Chemistry and Chemical Engineering，South China University of Technology，Guangzhou Guangdong 510640，China）

Cavity receiver plays an important role in the dish solar thermal power system．Its performance can affect the efficiency of the whole system．In the present work，the 2－D－model of six typical cavity receivers are created and FLUENT6．3 is used to investigate the approximate estimation of the natural convection heat loss of the cavity receivers．The six typical cavity receivers are calculated at the same aperture diameter（10 cm），the same wall temperature（400℃），and the same inclination（α＝0°）．The result of the present numerical procedure shows that the natural convection heat loss from the spherical cavity receiver is approximately 10%fewer than that of the other five．The effect of AW／A1（inner surface area／aperture area）on the convection heat loss has also been studied for the spherical cavity receiver at different inclinations．The convection heat loss is maximum at 0°（cavity aperture facing sideways）and decreases monotonically with increase in angle up to 90°（cavity aperture facing down）．The optimal AW／A1 for spherical cavity receiver ranges from 8 to 10．

solar thermal power；cavity receiver；natural convection；heat loss

TB34

A

1008－1542（2012）01－0044－06

2011－06－03；

2011－11－15；责任编辑：张士莹

国家自然科学基金资助项目（50206004）；广东省自然科学基金资助项目（020875）

龙新峰（1967－），男，江西九江人，副研究员，博士，主要从事强化传热与节能、热化学储能、太阳能热发电方面的研究。