复杂采空区处理方案的模糊推理系统

张东炜， 熊雪强， 赵 奎， 钟林传

(1.江西理工大学资源与环境工程学院，江西 赣州 341000；2.武平紫金矿业有限公司，福建 上杭 364200)

复杂采空区处理方案的模糊推理系统

张东炜1， 熊雪强1， 赵 奎1， 钟林传2

(1.江西理工大学资源与环境工程学院，江西 赣州 341000；2.武平紫金矿业有限公司，福建 上杭 364200)

对于复杂采空区的现状，采空区处理是亟待解决的问题.在选择充填和封闭联合处理采空区的前提下，通过使用关系矩阵与模糊数学联合的采空区稳定性分析方法，得到了各采空区的稳定性系数，结合采空区稳定性系数及地压监测结果，进行了采空区处理方案的模糊推理系统研究，通过研究能得到与每个采空区相适应的处理方法，为矿山的地压处理提供了相应的理论依据，并为矿山的安全生产提供了保障，同时也对类似采空区处理提供了一定的依据.

采空区处理；模糊推理；复杂采空区；采空区稳定性

0 引 言

空场法是目前使用较广的一种开采方法，但是该方法遗留下许多未处理的采空区，复杂的采空区可能会引发大规模的冲击性地压，造成不必要的财产及人员伤害，目前对采空区处理的方法大致分为崩落围岩处理采空区、充填料充填处理空区、留永久矿柱或构筑人工石柱处理空区、封闭和隔离处理采空区、联合法处理采空区[1].目前随着对环境保护要求的提高，使用充填法处理采空区越来越广泛.充填体主要有3种作用原理：应力吸收与转移，接触支撑和应力隔离[2].文中主要针对采用充填和封闭联合处理采空区时的具体区域进行研究.

目前对于采空区稳定性的分析方法很多，主要有理论分析、模糊分析、数值模拟分析.其中模糊理论分析运用较广.文中采用的基于关系矩阵与模糊数学的综合评价方法就是建立在模糊理论之上的一种有效的采空区稳定性分析方法，该方法考虑了6种采空区的主要影响因素，结合各影响因素的活动性指数与其对应的隶属度值算出各采空区稳定性系数，以此系数进行采空区稳定性的初步评价，但是，现场的情况往往是非常复杂的，且不断变化着.此方法中各主要因素隶属度的选取也有很大的模糊性，且不能反应采空区的动态变化，变化着的采场其稳定性只有通过地压监测才能有所反应，地压监测也具有一定的模糊性，为了能得到更加符合实际的结果，必须结合静态的采空区稳定性系数与动态的地压监测的模糊结果，而模糊推理系统便能有效的整合各种模糊输入变量，得到与实际相符的精确结果[3].下面详细介绍该模糊推理系统的建立.

1 模糊推理系统的建立

模糊推理系统主要由输入输出变量的模糊化、模糊规则库建立、模糊推理方法选择及去模糊化几部分组成.

1.1 关系矩阵及模糊数学联合的采空区稳定性分析

1.1.1 采空区稳定性的关系矩阵

由于影响采空区稳定性方面的因素很多，文中采取文献[4]和[5]所提出的关系矩阵及模糊数学的联合采空区稳定性评价方法，其选择的影响采空区稳定性的主要因素有：①岩石单轴抗压强度R；②顶板暴露面积A；③原岩应力状况；④结构面状况；⑤地下水W；⑥矿柱状况P.其中结构面状况又可以分为结构面间距D和结构面产状与顶板的方位关系O2个因素，原岩应力状况分为最大初始应力和围岩单轴抗压强度比值ST及最大主应力方向与采场顶板方位之间的关系SL 2个因素，各因素的相对重要程度使用活动性系数来衡量，系数越大则说明其对整个评价系统的贡献越大.主要因素aii的活动性系数由式（1）确定：

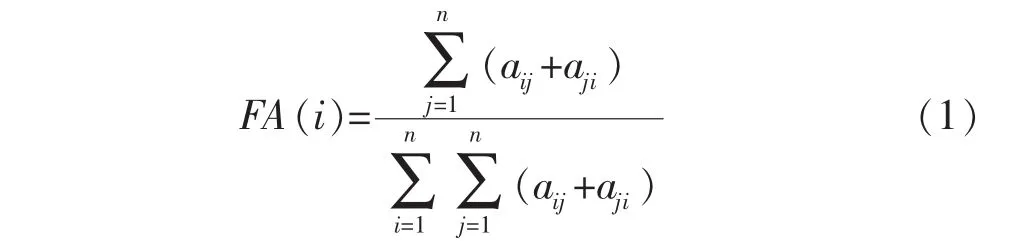
式中FA（i）对应的活动性系数，n为主要因素个数；aij为因素aii对因素aij的影响程度.

总结上述各主要因素之间的相互作用，依据其相互的影响强度，结合实践经验，给关系矩阵赋值，从而得出与其对应的关系矩阵，如式（2）所示：

从而由活动性计算式便可得到各活动性系数为：FA（1）=0.118， FA（2）=0.191， FA（3）=0.127，FA（4）=0.064， FA（5）=0.127， FA（6）=0.082， FA（7）=0.127，FA（8）=0.164.

1.1.2 采空区稳定性系数

由上述建立的关系矩阵，根据模糊数学理论选取与各影响因素合适的隶属度函数，其每个影响因素的隶属度函数的构造由于篇幅原因暂不进行详细概述，这里只介绍岩石单轴抗压强度与最大初始应力比值ST的隶属函数构造，实测资料显示，当ST为3～6时就会发生岩爆和岩心饼化，当在5～10和10～200时分别对应高、低应力，故由此选择隶属函数的特征点为3、6、10、200；各主要因素的隶属度函数曲线如下图1所示.

通过具体采空区的现状结合隶属函数选择对应的隶属度值，最终建立起采空区稳定性的评价指标，即采空区稳定性系数：各主要因素活动性评价指标FA（i）与其对应的隶属度 W（i）进行乘积，并将所有因素的乘积结果进行累加，其累加值就定义为采空区稳定性系数[6]，记为 MS，即：

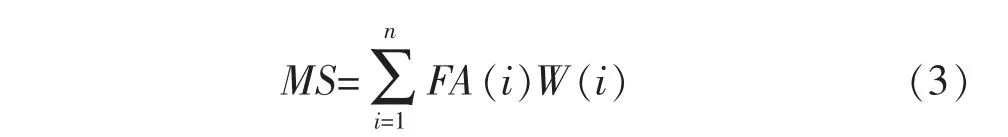
式（3）中：W（i）为主要评价因素的隶属度；FA（i）为前述的各影响因素活动性指数.

1.2 输入输出变量的隶属度函数确立

选择空区稳定性系数及地压监测结果作为输入变量，采空区处理方案作为输出变量，从静态和动态两个方面进行采空区处理研究，其结果符合实际状况，其中输入、输出变量可采用高斯型隶属度函数如式（4）所示：输入、输出隶属度函数具体建立过程如下.

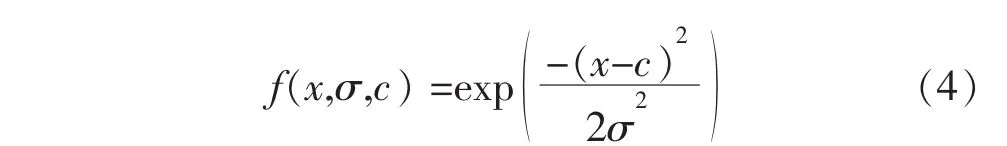
根据稳定性系数计算结果，将稳定性系数划分为3个变量：不稳定、中等稳定、稳定.结合许多其他开采矿山的采空区赋存状况进行空区稳定性的计算分析，发现采空区稳定性系数一般在0.5附近，故选择采空区系数在0.5时对应于中等稳定的隶属度为1，稳定与不稳定隶属度函数曲线则随着稳定性系数的增大而分别增大和减小，函数曲线如图2所示.

现场监测使用最广泛的监测仪器便为光弹应力计，因为其低价实用，故文中所有监测数据均针对光应力计结果，地压监测结果主要包括应力大小和一段时期的应力增量大小，应力增量有正负之分，其中正说明处于应力集中状态，负则说明处于应力释放状态.监测应力的大小与许多因素有关，如仪器布置离空区越近则其所受的力越大，且埋藏越深对应的应力也越大，反之亦然，所以仅仅依靠应力大小无法确定应力集中区域，只能作为判断的因素之一，故同时选择应力增量作为影响采空区处理的另一个重要因素，应力增量可以看作采空区在一定时期内其内部的动态变化，应力及应力增量在排除施工因素的影响后能反应监测区域的应力集中状况.

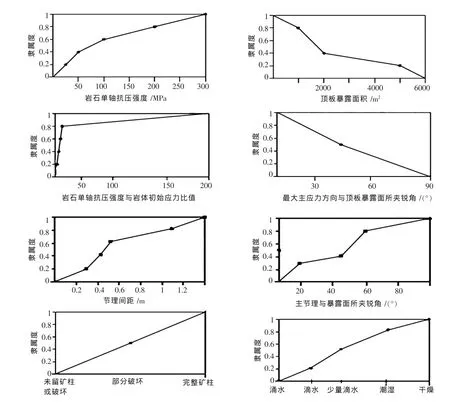
图1 各主要因素隶属度函数曲线

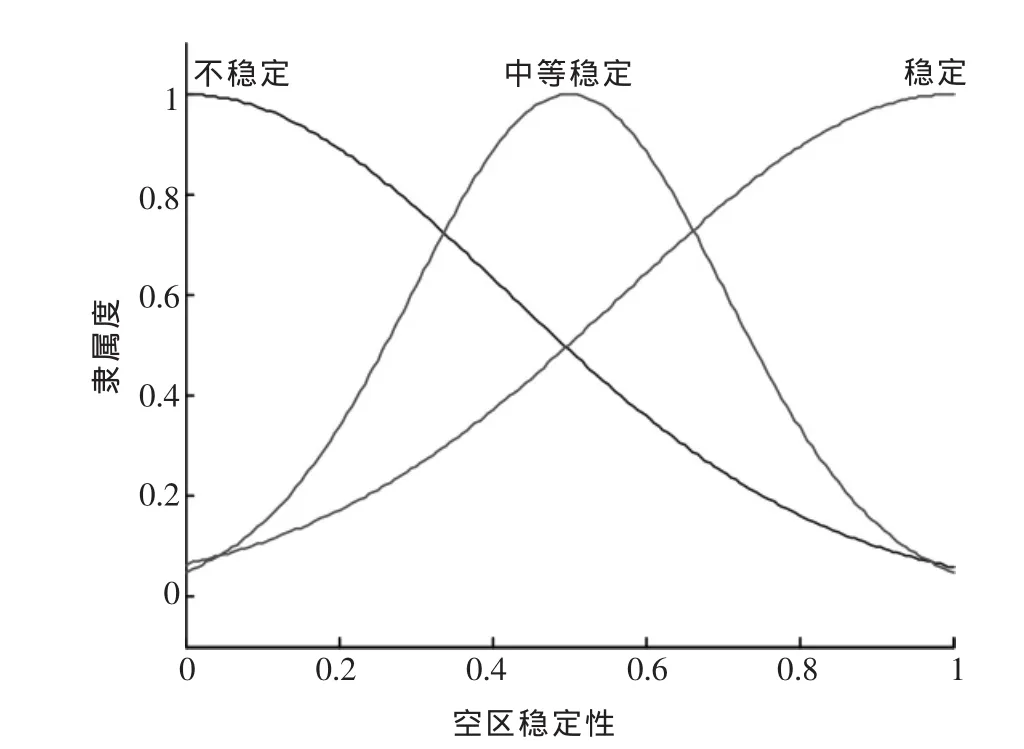
图2 空区稳定性隶属度函数曲线图

对于监测的应力增量，如何判断其危险性大小，目前只有依据其与矿柱的强度进行比较，而矿柱影响因素也非常复杂，对于目前许多对矿柱强度计算的公式，选择最具代表性的公式，如式（5）所示：

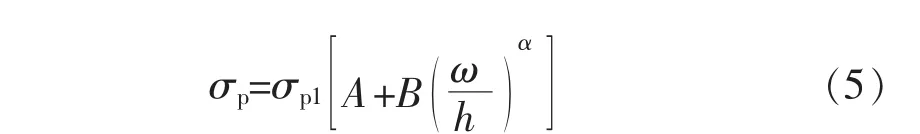
其中：σp为矿柱的强度，/MPa，σp1为宽高比为1时的矿柱强度，/MPa，ω、h分别为矿柱的宽度和高度，/m，其他为不同岩体所对应的常系数.

在这类公式中选择较为广用的Bieniawski提出的强度公式,如式（6）所示：

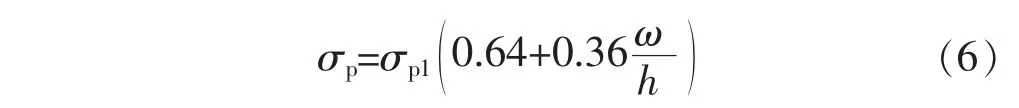
由于上述未考虑节理裂隙对矿柱的影响，为此采用Hoek-Brown计算节理岩体强度的方法作为σp1的计算公式，即：

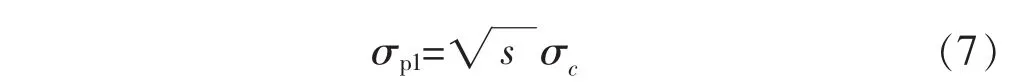
式（7）中 σc为完整岩石的单轴抗压强度，/MPa；s表示岩体完整性的一个常数.对于含有多组节理且没有明显的各向异性的岩体s值由式（8）确定：

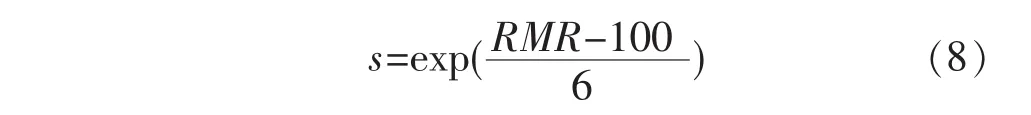
其中RMR为岩体地质分类指标.

对于矿柱的平均应力的计算也有很多方法，但是其由于模型进行了简化，计算结果与实际相差很大，因为它们均为考虑原岩应力的影响，为此选择公式（9）作为矿柱平均应力的计算：

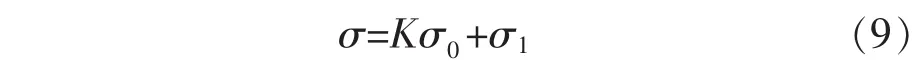
其中K为采场开挖前的矿柱集中系数，一般取1～2；σ0为原岩应力，/MPa，可以取自重应力；σ1为二次回采增量即为我们监测过程中的应力增量，/MPa.

通过上述对矿柱强度的计算，用矿柱强度除以矿柱平均应力便能作为衡量矿柱危险性大小的一个系数，称为安全系数[7]，具体公式如式（10）所示：

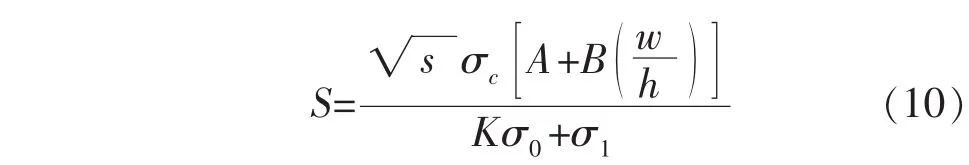
安全系数S与应力增量σ1的关系可近似作为选取应力增量隶属函数的依据.通过大量矿柱现场实测资料结果发现安全系数小于1对应的矿柱破坏严重，一般大于2时矿柱都很稳定，故选择安全系数范围在0～3之间，同样把安全系数也划分为3个变量：不稳定、中等稳定、稳定.其对应的隶属度函数如图3所示.

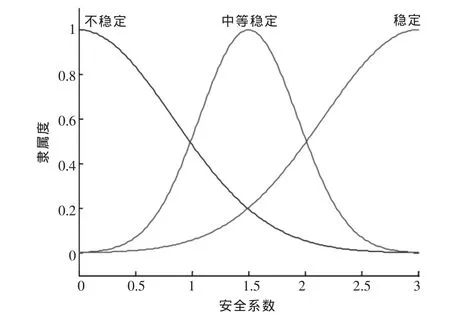
图3 安全系数隶属度函数曲线图

通过对许多矿山光应力计的实际监测结果分析，发现光应力计条纹级数大的区域应力均比较集中，因为附近也必然伴随着一些地压显现，在对铜陵紫金的现场监测发现光弹应力计压坏后其矿柱也随之破坏，室内试验得到光应力计所能承受荷载约为7 MPa，故应力的选取范围为0～7 MPa，同时对各矿山的监测数据进行统计分析，一般选取0～3 MPa范围内所监测区域为稳定区域，3～5 MPa为中等稳定区域，5～7 MPa为不稳定区域.故将应力水平也划分为3个变量：不稳定、中等稳定、稳定.函数曲线如图4所示.

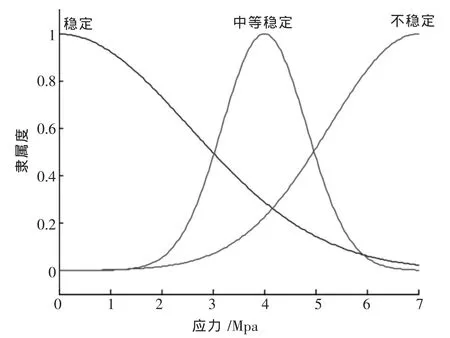
图4 应力隶属度函数曲线图

输出变量则为采空区对应的处理方案，分别对应充填、封闭、暂不处理.函数曲线如图5所示.

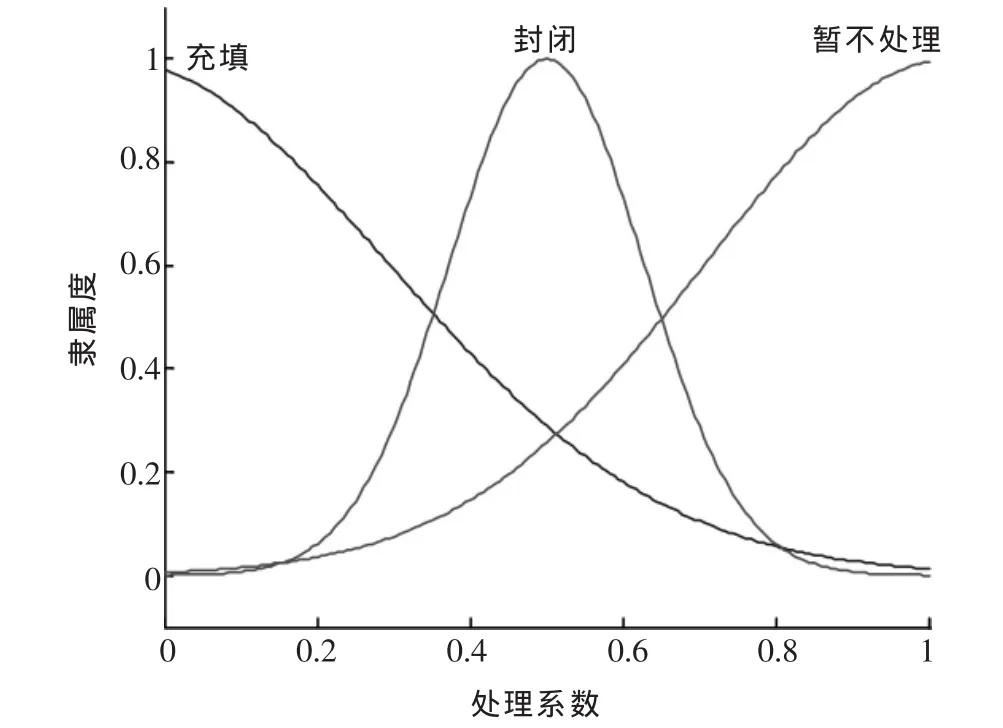
图5 处理方案隶属度函数曲线图

1.3 模糊推理系统规则库建立

模糊规则库代表着整个推理系统的思考法则，其产生方式一般有3种方法：①直接由操作员的经验技巧建立模糊规则；②根据受控体对输入与输出的反应去归纳受控行为，以误差法进行设计；③控制系统本身进行学习或修正控制规则.文中采用第一种方法建立模糊规则库，模糊规则以if-Then条列式的形式，表示结合了人类判断的模糊性控制法则，每个控制规则由前后件组成，通式如式（11）所示：

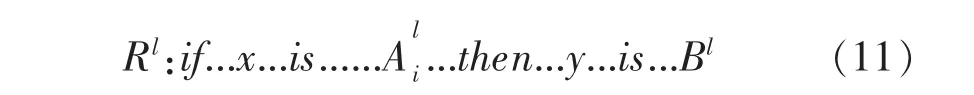
其中Rl即表示第l条规则；x为输入及 Bl为对应于变量的模糊集合；y为输出，用来控制受控系统.依据实际情况共建立27条规则，其结果如表1所示.其蕴含的规则思想选择第一条规则进行解释即：if输入的空区稳定性系数对应不稳定，安全系数对应稳定且应力对应稳定，then处理方案选择封闭.表1考虑了所有可能的情况，因此能满足实际情况.

表1 模糊规则库

1.4 模糊推理系统的合成

依据实际选择Mamdani推理算法作为模糊推理系统的合成算法[8]，该算法与Zadeh提出的推理合成算法本质相同[9]，是在选择合理的规则后，就建立了一种模糊蕴含关系，在该蕴含关系下选择各因素的计算或分析结果作为输入，对输入结果进行模糊化处理后得到各规则对应的模糊集，将该模糊集作为输入，经合成处理后得到的一个综合模糊集作为输出.最后选择合适的反模糊化方法将综合模糊集以确定的数值形式输出.一般采用重心法来求出精确值，文中采用中心法作为反模糊化方法.

由上述输入、输出变量及规则库结果，运用Matlab模糊逻辑工具箱建立模糊推理系统.其对应的不同变量之间的关系曲面图如图6～图8所示.

通过对输入输出曲线、曲面检验：输入变量采空区稳定性系数、安全系数、应力具有等价性，通过对单输入曲线得到应力为递减函数，空区稳定性及安全系数均为递增函数，说明与实际相符合，对应的隶属度函数及规则的确定是合理的.

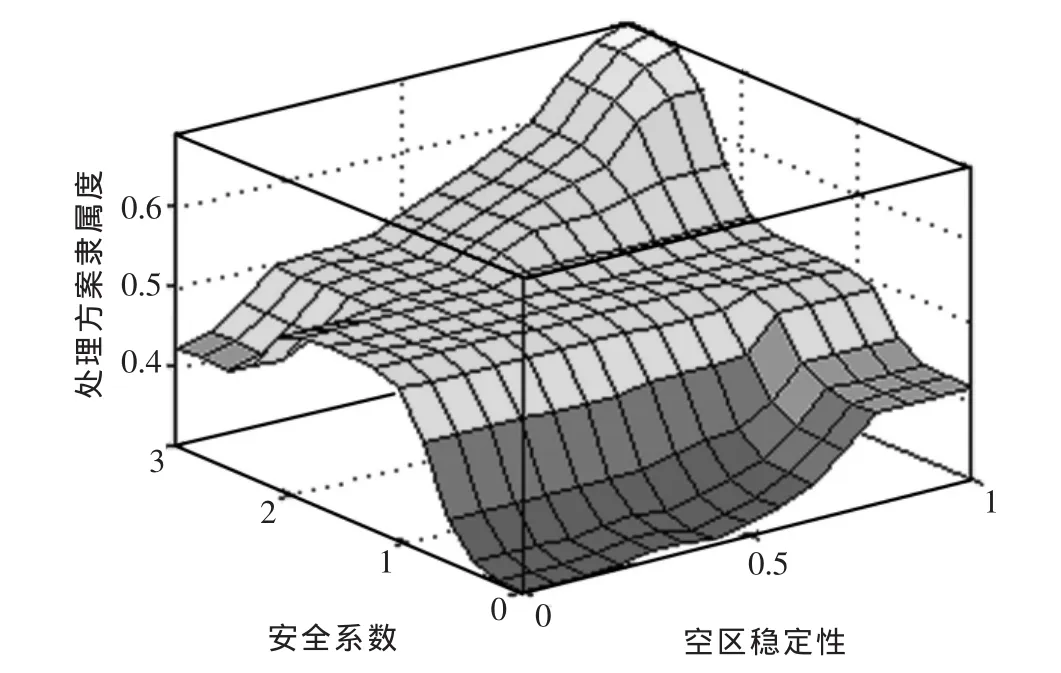
图6 安全系数与空区稳定性系数关系曲面图

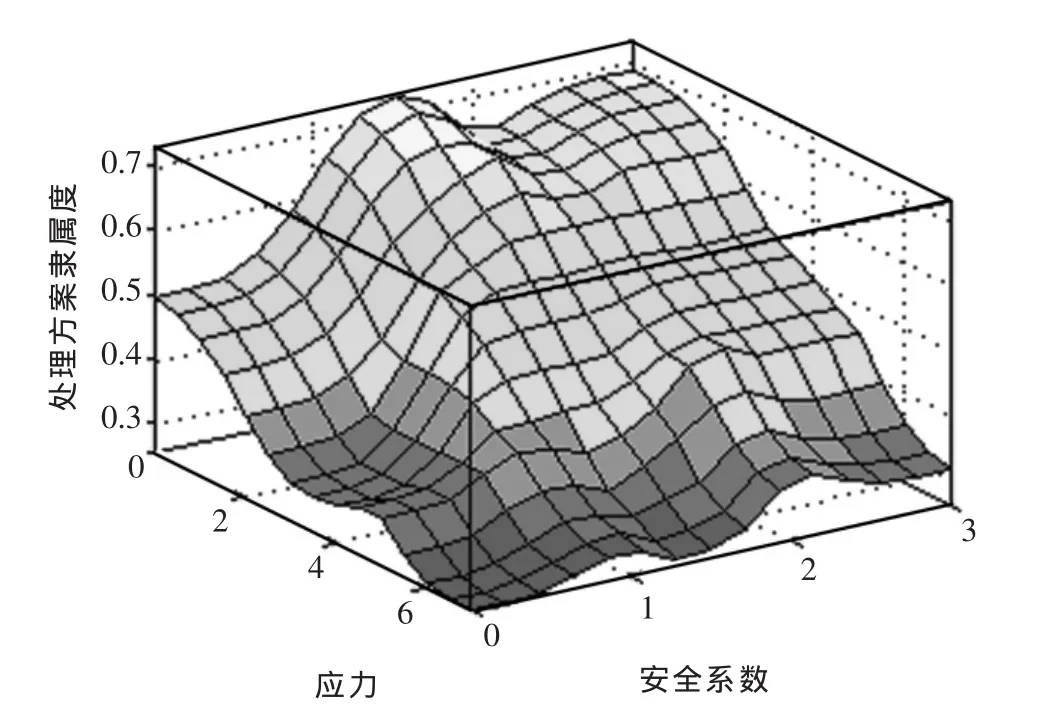
图7 安全系数与应力关系曲面图

2 应用实例

2.1 输入变量分析

武平紫金矿业有限公司悦洋银多金属矿是2007年1月由紫金矿业集团股份有限公司出资收购的民营企业，矿山主要采用空场房柱法进行开采，至今形成了超过约61.5万m3采空区，通过对矿山各中段的现场调查及点荷载试验获得了各采空区的赋存状况及岩石的力学参数，通过调查结果共布置77个应力监测仪器，其中光弹应力计60个.得到数据几千个，采用上述采空区稳定性分析方法对每个采空区进行了稳定性系数计算，并通过地压监测得到各采空区相应测点的应力及应力增量值，由应力增量算出其对应的安全系数，由于篇幅有限故只列举-145 m中段部分空区数据，如表2所示.

其中采空区稳定性采用前述计算方法，-145 m中段主要回采矿体为Ⅰ号矿体.矿体受花岗岩“舌状体”与楼子坝群变质岩接触带控制，岩石普遍绿泥石化，围岩单轴抗压强度在30～95.9 MPa.该中段与表2对应的采空区暴露面积分别为 1076.7、182.7、1259.4、140、196.2、829.0 m2；结构面间距主要集中在10～20 cm，倾角在 30～80 °；自重应力 rH=9.1 MPa；中段留矿柱大部分已破坏，空区内见少量滴水.选用相应隶属度后计算空区稳定性系数结果见表2.

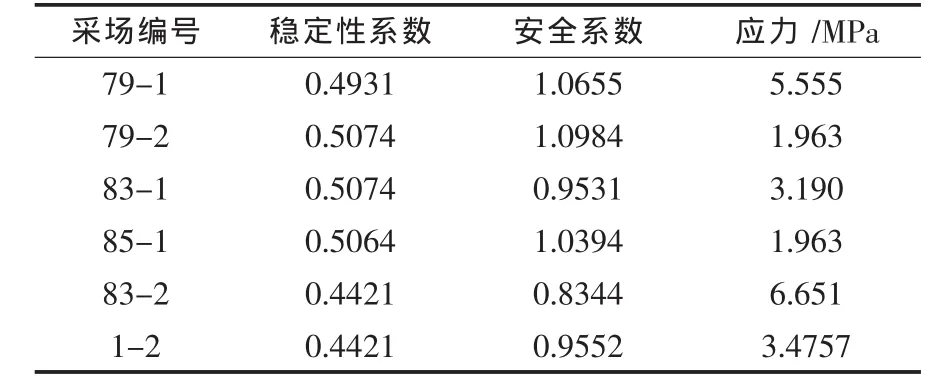
表2 -145 m中段部分空区稳定性系数表

通过前期调查及试验可知矿体赋存岩石为中细粒花岗岩，其抗压强度经点荷载试验转换约为135 MPa，矿柱宽高比选1，RMR经计算约为70，K取1， 自重应力取 10.4 MPa，A、B按 Bieniawski提出的强度取值分别取0.64、0.36[10-11].应力增量取前后2次监测应力的差值，通过计算其对应结果如表2所示.

应力值有光弹应力计监测条纹经转换后的应力值[12]，同时也有钻孔应力计监测的直接应力值.其中采空区附近多组监测结果选取其中应力最大值作为代表.如83-2采空区选取最大6.651 MPa代表该区域应力.

2.2 模糊推理系统计算结果

通过建立起来的模糊推理系统使用evalfis函数根据已有的各组计算结果计算出与其相对应的采空区处理系数，-145 m中段处理系数分别为：0.3404、0.5498、0.4847、0.5250、0.2949、0.4697 通过系数确定不同的采空区的处理方法，通过对输出变量的隶属度函数观察，3条隶属函数曲线的交点为0.35和0.65，即这2点可以理解为最模糊点，故以此作为其处理方案的依据：系数在0～0.35之间的选用充填处理采空区；系数在0.35～0.65选择封闭处理采空区；0.65～1选择暂不处理采空区.故-145 m中段79-1、83-2 采空区采取充填处理；83-1、85-1、83-2、1-2 采区封闭处理.

3 结束语

文中通过地压监测结果、以及采空区稳定性系数建立了采空区处理的模糊推理系统，得到了复杂采空区群下各个采空区的处理系数，为每个采空区的处理提出了具体的处理方案，能起到缓解地应力集中的状况，保障作业安全，对类似矿山采空区处理也提供了一定的依据.

由于输入、输出变量的隶属度函数的选取有一定人为因素的影响，同时规则库的建立也包含了许多模糊因素，因此其处理结果还不能排除人为因素的影响，只能在此基础上逐渐逼近实际结果，故在这些方面还有待于进一步的研究.

[1]罗毅莎，姚振巩.采空区安全处理的对策措施研究[J].采矿技术，2010，10(4)：65-67.

[2]赵传卿，胡乃联.胶结充填对采场稳定性的影响[J].辽宁工程技术大学学报，2008，27(1)：13-16.

[3]赵 奎，万林海，饶运章，等.基于声波测试的矿柱稳定性模糊推理系统及其应用[J].岩石力学与工程学报，2004，23(11)：1804-1809.

[4]赵 奎.岩金矿山采空区及残留矿柱回采稳定性研究[D].赣州：南方冶金学院，2003.

[5]钟春晖，赵 奎，郭秋根，等.基于关系矩阵和模糊理论的采空区稳定性综合评价[J].采矿科学技术前沿论坛论文集，2006，44-46.

[6]马尚权，王立兵.基于关系矩阵和模糊集合的煤与瓦斯突出综合评价[J].现代矿业，2001，15(10)：49-51.

[7]赵 奎.矿山岩石力学若干测试技术及其分析方法[M].北京：冶金工业出版社，2009：31-35.

[8]吕大江，石志寒，雷英杰，等.基于Mamdani蕴含关系的直觉模糊推理仿真[J].计算机工程与设计，2010，31(11)：2539-2542.

[9]闻 新，周 露，李东江，等.MATLAB模糊逻辑工具箱的分析与应用[M].北京：科学出版社，2011：41-45.

[10]赵 奎，胡慧明，王晓军，等.某金矿房柱法采场人工矿柱参数选取[J].采矿技术，2011，11(2)：15-17.

[11]Z.T.Bieniawski.Estimating the strength of rock materials[J].J.S.Afr.Inst.Min.Metall，1974（74）：312-320.

[12]郭建平.光应力计监测采空区稳定性在遂昌金矿的应用[J].有色金属，2004，56(3)：115-117.

Complicated goaf treatment scheme of fuzzy inference system

ZHANG Dong-wei1，XIONG Xue-qiang1，ZHAO Kui1，ZHONG Lin-chuan2

(1.School of Resource and Environmental Engineering,Jiangxi University of Science and Technology,Ganzhou 341000,China；2.Zijin Mining Co.Ltd.，Shanghang 364200,China.)

This paper studies the stability coefficients of the mined out area by using the fuzzy relation matrix and joint stability analysis goaf under the premise of using the fuzzy relation matrix associated with the goaf stability analysis method.Combined with the stability of mined-out area and ground pressure,goaf treatment options of fuzzy inference systems are obtained.

treatment of mined goaf;fuzzy reasoning；complicated goaf；stability of goaf

TF065.1；TG111.3

A

1674-9669（2012）01-0089-06

2011-11-12

国家重点基础研究发展计划资助项目（2011cb411913）

张东炜（1985- ），男，硕士研究生，主要从事岩石力学方面研究，E-mail：zhangdongdelove@yahoo.com.cn.