海森堡不确定性原理的教学研究
2012-12-27谢勇
谢 勇
(大理学院工程学院,云南 大理 671003)
海森堡不确定性原理的教学研究
谢 勇
(大理学院工程学院,云南 大理 671003)
海森堡不确定性原理在量子力学的教学中占有很重要的地位.通过概念引入,实验分析,理论证明以及量子力学例证,介绍了一种海森堡不确定性原理的教学模式.
海森堡不确定性原理;教学;量子力学
海森堡不确定性原理(Heisenberg uncertainty principle)是由德国物理学家海森堡于1927年提出的量子力学中的不确定性,具体指在一个量子力学系统中,一个粒子的位置和它的动量不可被同时确定[1].由于海森堡不确定性原理与经典物理的观念是截然不同的,在教学上有一定的难度.本文将对海森堡不确定性原理的教学引入、理论证明,以及例证进行研究讨论.
1 海森堡不确定性原理的教学引入
1.1 概念的引入
量子力学所讨论的波是一种概率波.根据de Broglie关系,与一个单色平面波(波长为☒,频率为n)对应的粒子的动量.如果用表示粒子的动量分布函数,则可以由Fourier展开得到[2],
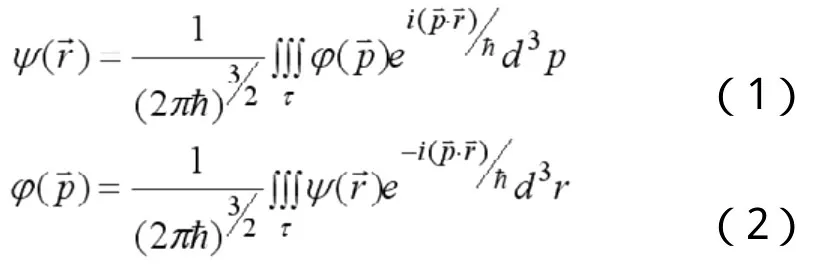
1.2 实验分析
微观粒子的位置与坐标的不确定性原理可以通过物质波的单缝衍射实验来加以说明.如图1所示,设单缝的宽度为,物质波(如电子波)的波长为☒,从衍射强度的中心极大到第一极小的夹角为☒,则根据单缝衍射公式[2]

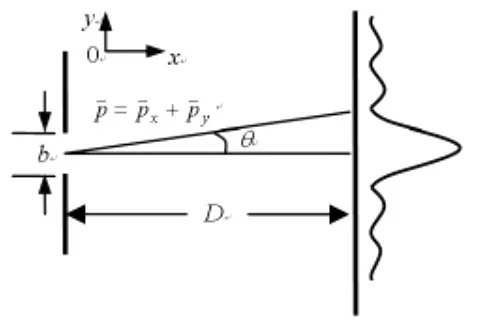
图1 物质波的单缝衍射
粒子在穿过狭缝之前是沿x方向运动的,即粒子动量的竖直分量为零.由于微观粒子的波粒二象性,当粒子穿过狭缝以后,其动量的竖直分量 将发生改变. 的大可通过粒子抵达探测屏的位置计算出来.如图1所示, 的不确性 大约

由于☒很小,所以结合(3)式,得

当粒子穿过狭缝时,粒子位置的不确定性 显然就是狭缝的宽度,

于是,有

根据德布罗意的物质波假说[3],

式中h为普朗克常数,故有

这就是海森堡不确定性原理的实验估算.
2 海森堡不确定性原的理论证明
对海森堡不确定性原理的理论证明有很多方法[3-5],在实际教学中,我们主要参照文献[5]提供的方法.这种方法简洁易懂,学生很容易接受.
根据方差的定义,某一厄米算符 的方差为
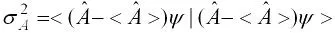
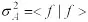
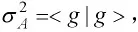
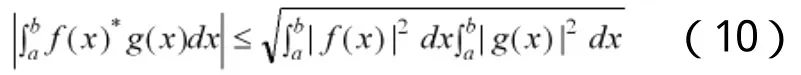
得


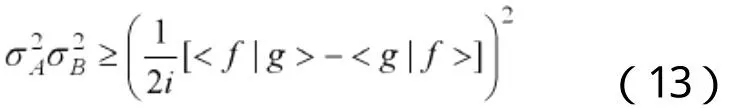
而
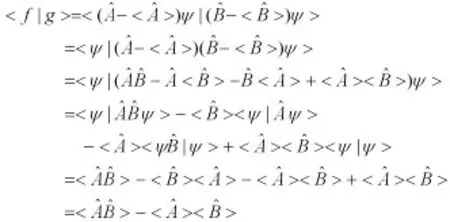
以上的推导用到了算符的厄米性和波函数的归一性.同理可得,
于是,

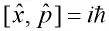
所以,

由于标准差为非负数,所以

这就是海森堡提出的坐标与动量的不确定性原理的数学形式.
3 海森堡不确定性原理的量子力学例证
海森堡不确定性原理适用于所有微观粒子的量子行为.教学中,通过粒子的坐标表象及动量表象波函数来验证不确定性原理,对于学生理解微观粒子的波粒二象性和不确定性原理有很好的帮助.例如对于一维谐振子,其基态波函数为[3],
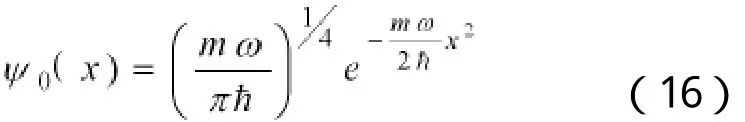
可以用解析法来验证不确定性原理,但计算较为繁琐.教学中,我们主要使用升降算符来进行验证.利用一维谐振子升降算符的定义和递推公式[5]:

及
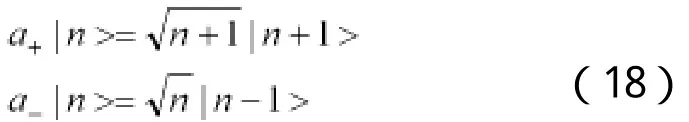
有
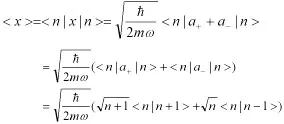
由正交归一条件[3]

得

同理,

对于坐标的方均值,
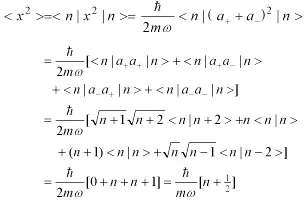
同理得动量的方均值,
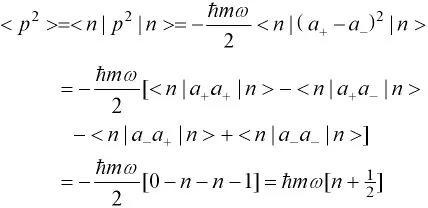
将上述结果代入坐标与动量的方差公式:
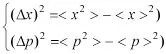
得
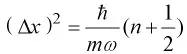
和
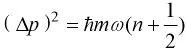
于是
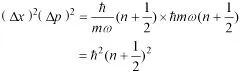
故有

由于量子数n的取值是0, 1, 2, …,所以

此结果与(15)式完全相符.
4 讨论
海森堡不确定性原理贯穿于量子力学的整个教学中.我们首先通过坐标与动量的Fourier变换,从概念上引入了坐标与动量不能同时被准确确定的性质,然后通过物质波的单缝衍射实验,估算出这种不确定性的数量级.在介绍算符的运算规则的时候,我们利用西瓦茨不等式严格证明了海森堡不确定性原理.随后的教学讨论中,我们要求学生根据所学知识,在课堂上对海森堡不确定性原理进行验证,例如本文介绍的一维谐振子的例证.这样的教学安排可以使学生对微观粒子的波粒二象性有更深刻的理解.
[1]W.Heisenberg. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik[J]. Physics,1927,43(3-4):172-198.
[2]马文蔚等.物理学教程:第二版[M].北京:高等教育出版社,2010.
[3]曾谨言.量子力学教程:第二版[M].北京:科学出版社,2008.
[4]绰英超.广义Heisenberg不确定关[J].大学物理,1997(2):31-33.
[5]David J.Griffiths.Introduction to Quantum Mechanics[M].Benjamin Cummings;2 edition (2004).
Research on Teaching Heisenberg Uncertainty Principle
XIE Yong
(College of Engineering, Dali University, Dali 671003, China)
Heisenberg uncertainty principle is very important in quantum mechanics. This paper introduces a teaching mode for Heisenberg uncertainty principle through importing concept, experiment analyzing, theoretically prove, and example illustration.
Heisenberg uncertainty principle; teaching; quantum mechanics
O413.1
A
1008-9128(2012)04-0008-03
2012-03-28
中德科学基金项目(GZ585)
谢勇,副教授.研究方向:理论物理和生物医学工程学的教学与研究.
[责任编辑 张灿邦]
