应用于电流型数模转换器的积分非线性误差优化方法

傅文渊，凌朝东

（1.华侨大学 信息科学与工程学院，福建 厦门361021；2.厦门市专用集成电路系统重点实验室，福建 厦门 361008）

应用于电流型数模转换器的积分非线性误差优化方法

傅文渊1，2，凌朝东1，2

（1.华侨大学 信息科学与工程学院，福建 厦门361021；2.厦门市专用集成电路系统重点实验室，福建 厦门 361008）

提出一种新型积分非线性优化方法，即在电流源上分别并联两组控制信号与原电流源的控制信号相反的辅助伪差分共源共栅MOS管，其电流源产生一个与原共源共栅电流源相反的积分非线性偏差，极大减小数模转换器的积分非线性和开关毛刺现象.仿真结果表明，优化后的积分非线性减少96%，数模转化器的有效转换位数增加了2.1bit，无杂散动态谐波范围增加了15dB；未优化前的积分非线性设计与Monte Carlo仿真结果有500%的偏差，而优化后的偏差仅为60%.

数模转换器；电流型；积分非线性；电流源

近年来，随着电子通讯市场的快速发展，尤其是物联网的提出，以及数字高清音视频和3G无线通讯网络的开发应用，极大提高了对数模转换器（digital－to－analog converter，DAC）精度和速度的要求［1-2］.影响数模转换器性能，主要有时钟抖动、毛刺、有限输出阻抗、电流源随机偏差［3-5］，而有限输出阻抗是决定转换器动态特性和静态特性的关键的因素之一.电流型数模转换器是电流源在输出端电流相加而形成的，所以电流源的准确程度直接影响转换器的性能.电流源的准确程度受制于以下3个因素：1）电流源由集成电路工艺偏差而造成的失配；2）高速信号传输使高频的噪声会通过电容耦合到电流源晶体管的栅上，从而影响电流源的准确程度；3）加载在电流源栅极上控制信号的不同步而引起的低频干扰.积分非线性（integral nonlinearity，INL）是实际和理想的有限精度特性在转移特性曲线垂直方向上的最大值.文献［6］用Monte Carol来分析器件失配对积分非线性的影响，这在高精度数模转换器设计中是非常耗时的.文献［7］为数模转换器建立了准确的统计模型，描述速度、精度和单位电流标准差之间的关系，但其设计非常繁琐，效率较低.文献［8］采用主从数模转换器设计，消除三阶互调（third－order intermodulation，IM3）的谐波能量，增大输出阻抗而减小积分非线性.本文从积分非线性原理出发，提出一种适用于电流型数模转换器的积分非线性优化方法.

1 理论分析

图1为电流型数模转换器的系统行为模型.图1中：I，Rm和Rl分别代表单位电流源的电流、输出阻抗和负载阻抗；clk和nclk代表电流源栅极控制时钟信号；D1，D2，…，DN代表单位电流源的序列号，N为单位电流源总的个数.对于n位数模转换器来说，共有N＝2n－1个单位电流源，则由图1可得积分非线性的表达式［9］为

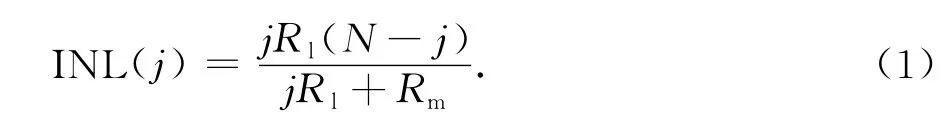
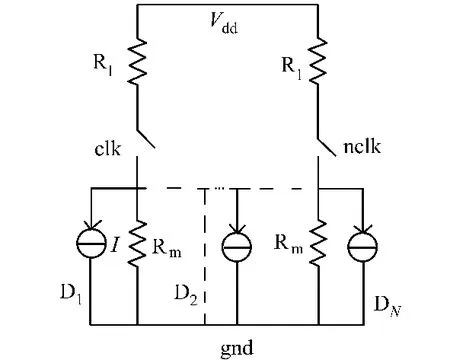
图1 电流型DAC系统图Fig.1 System diagram of current DAC

电流源采用共源共栅结构增加输出电阻，通过差分开关来选通电流源到输出以形成位电流.要使电流失配最小，必须使过驱动电压达到最大，但过驱动电压的最大化受制于供电电压源的限制（必须使所有晶体管工作在饱和区），同时使芯片面积增大.差分输出可以有效避免数模转换器信号频谱中的二次谐波能量，提高总谐波失真（THD）和无杂散动态谐波范围（SFDR）.对于图1，令Rmx1＝1，Rlx2＝1，Rnx3＝1，则其差分输出电压和积分非线性分别为

比较式（1）和式（3）可知，式（1）中当数字码为0或者N时，积分非线性为0，而（3）中积分非线性为0的情形是数字码为0，N／2和N.即采用差分输出，积分非线性为0的情形是单输出的1.5倍.当输出阻抗趋于无穷大时，式（1）和式（3）趋于0，因此非线性误差也趋于0.当电源压降在25%范围内变化时，电流源的每个MOS管的过驱动电压将不断变化，栅极控制信号剧烈变化，引起电流源输出阻抗急剧变化，积分非线性增大.

2 积分非线性优化方法

基于上述理论分析，针对电流型DAC提出一种新型的INL线性优化方法，其优化电路如图2所示.图2中：M1，M2，M3和 M4是电流源；M5，M6，M7和 M8，M9，M10是辅助共源共栅MOS管.图2是在图1的每个电流源上，分别并联两组控制信号与原电流源的控制信号相反的辅助伪差分共源共栅MOS管.在任意时刻tj，数模转换器有j个电流源和N－j个辅助共源共栅MOS管同时开启，辅助共源共栅MOS管产生一个与原共源共栅电流源相反的积分非线性偏差，两者综合可以极大地减小积分非线性误差.

从图2可知，M7和M10采用伪差分开关，能以最小的建立时间迅速切换，实现电路的控制信号和转换器的模拟部分之间良好的隔离.当反向伪差分管处于关闭状态时，要避免差分开关管同时关闭，信号下降的速度小于上升的速度，提高差分信号的交叉点.MOS管在器件导通时，其源极和漏极之间没有内在的直流漂移电压，而MOS管的控制通道和信号通道之间阻抗非常高，因此没有直流电流流过.

由于开关M3，M4是对称结构，若栅信号完美反相，两对开关对节点的影响正好抵消 .但是为了差分开关不同时关闭，要求上升信号加快到达高电平，这会在开关管的源端产生明显的电压跳变，导致开关对M3和M4的CGS，CGD流过一个瞬时电流.由于开关漏端是电流源的输出端，因此CGD流过的电流直接导致输出出现毛刺.在M3和M4基础上增加M7和M10的互补开关，可以减少毛刺现象.当栅信号上升时，寄生电容会有流向开关的源、漏的电流，输出理应有正的毛刺；但栅信号上升比下降速度快，且流入的空穴会因为另一个开关加速打开而被抽取过去，因此没有明显负的毛刺.

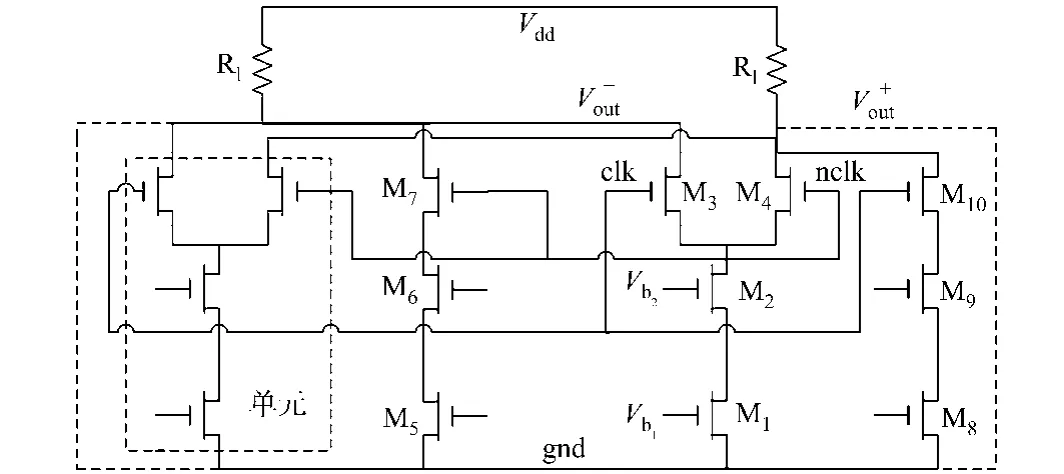
图2 积分非线性优化电路Fig.2 Optimization circuit of integral non－linear

由于M5和M6形成一个共源共栅MOS管，它通过的工作电流一定，因此漏端电压变化引起交叉节点电压变化非常小，电流镜输出毛刺大大减小.同时，单位电流源输出电阻将增加μnCOX（W／L）（VGS－VTH）Rm倍，改善了数模转换器输出线性度，减小了积分非线性.

图3为图2的系统行为级等效电路 .图3中：j为转换的数字码；I为单位电流源通过的电流；Ix为辅助伪差分共源共栅电流源通过的电流.进行数学代换p＝Nx1＋x2，q＝Nx3＋x2，t＝pq（Ix＋I）／（（Ixp－Iq）（pq）），则差分输出电压为

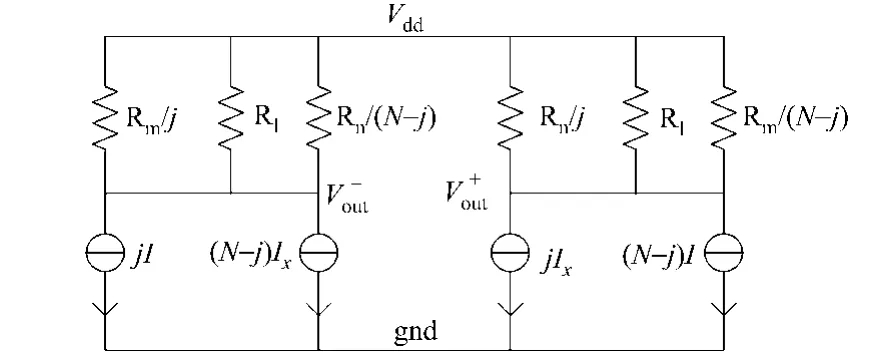
图3 差分输出的行为级等效电路Fig.3 Equivalent circuit of differential behavioral output

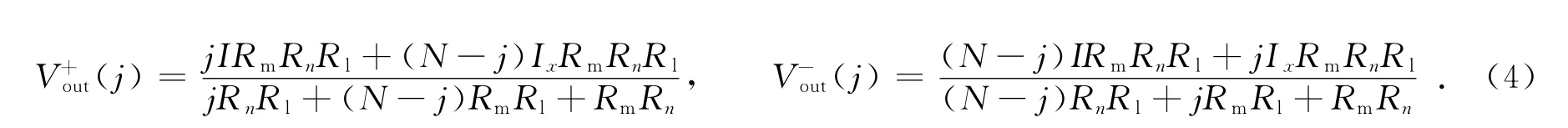
因此，经化简可得

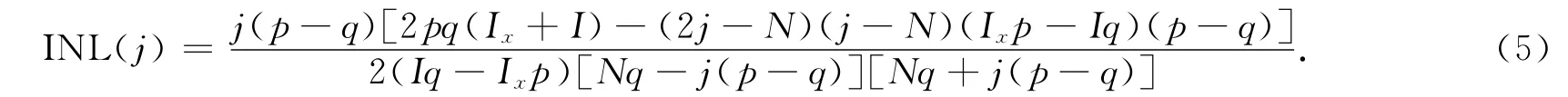
由于x2≫x1，x2≫x3，x1－x3≪Nx3＋x2，也就是（p－q）／（Nq）≪1，故式（6）可化简为

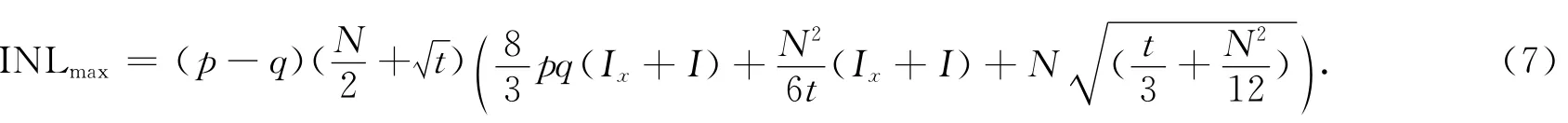
由式（6）可知，当p＝q时，即电流源的输出阻抗等于辅助伪差分共栅电流源的输出阻抗，INL（j）＝0，数模转换器无非线性失真.在数模转换器电流源的设计中，也必须使得Rm与Rn尽量相等 .由于式（6）为p，q的弱相关二次函数，因此INL（j）接近于0.做定量分析，设p＝m·q，则有

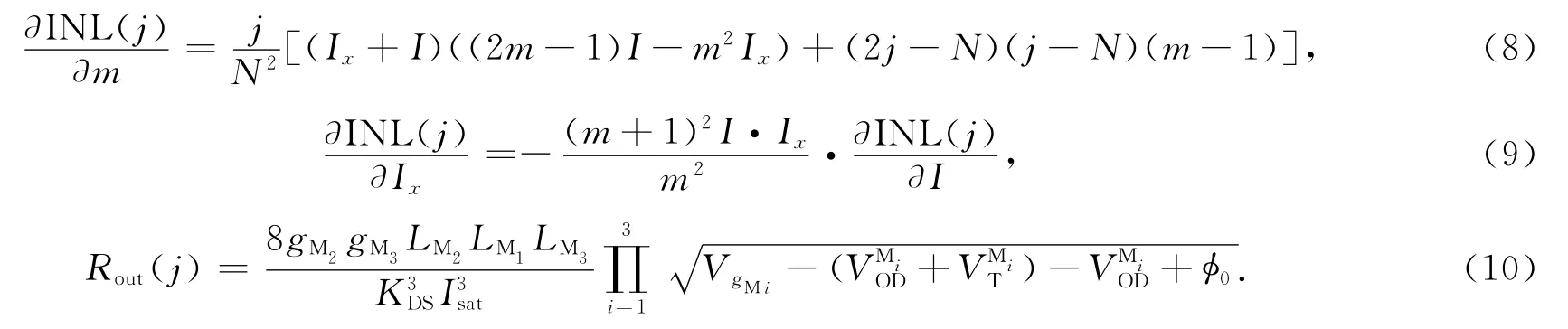
由式（8），（9）可知，当m＝1和m＝0.5时，积分非线性都随着输入数字码的增加而增加；当m为1时，式（8）为j的弱函数；当m＞1时，积分非线性随着输入数字码的增加而增大；当1＜m＜0.5时，积分非线性随着输入数字码的减小而增大 .因此，p接近q时，积分非线性的变化接近于0.

3 仿真实验

针对提出的方法，采用0.25μm MM－RF CMOS工艺进行仿真实验.实验的计算机硬件主要性能指标：Pentium Dual－Core T4200（2.00GHz）的CPU；2.00GB的 RAM；320GB的硬盘；计算机软件为MATLAB 7.6，LINUX HSPICE；集成芯片测试仪等.分别采用单位共源共栅电流源和辅助伪差分共源共栅电流源设计10位数模转换器，其积分非线性波形如图4所示 .图4中：10位电流型数模转换器的差分输出阻抗为100Ω，满量程输出电流为20mA，积分非线性最大为0.2LSB（最低有效位，下同）；通过单位共源共栅电流源的电流I为19.5μA，通过辅助伪差分共源共栅电流源的电流Ix为12.5μA.

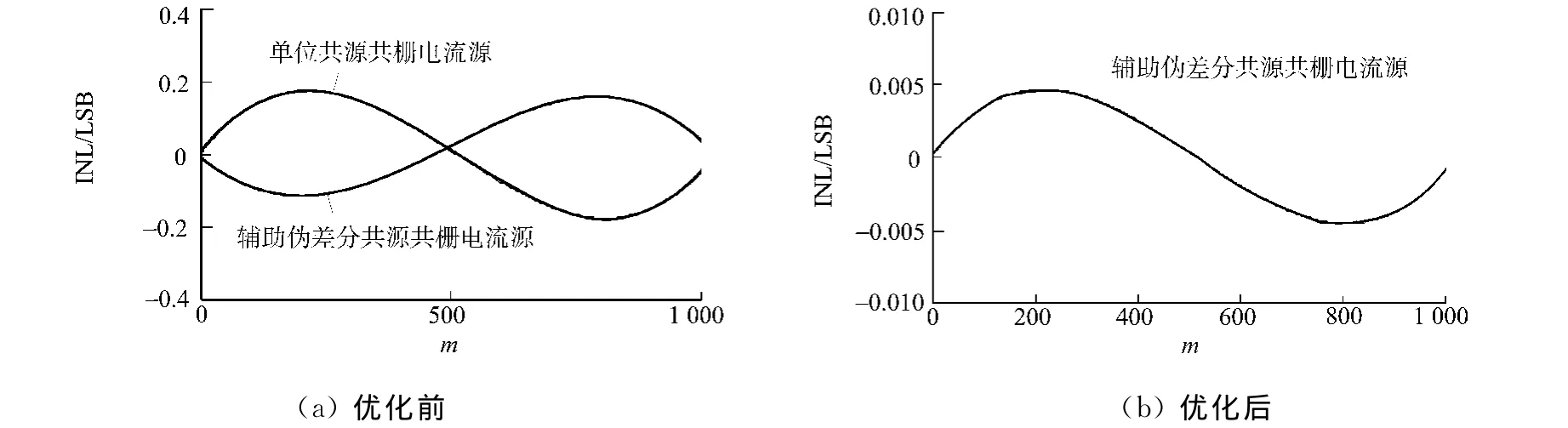
图4 数模转换器优化前后的积分非线性波形图Fig.4 Before and after optimized INL waveform for DAC

实验表明，采用单位共源共栅电流源设计的10位数模转换器，其积分非线性误差INLmax为0.18 LSB，而采用辅助伪差分共源共栅电流源设计的10位数模转换器，其优化前后的积分非线性误差INLmax分别为0.12，0.004 8LSB.

数模转换器优化前后的无杂散动态谐波范围的仿真波形图，如图5所示 .从图5可知，时钟采样速率为400MHz，输入信号频率为39.843 75MHz，优化后的SFDR提高了15dB，同时转换器的有效位数也有较大的提高.优化前的有效转换位数（effective number of bits，ENOB）为7.876 4bit，辅助伪差分共源共栅电流源的ENOB为7.234 6bit，优化后的ENOB为9.992 7bit，提高了2.116 3bit.

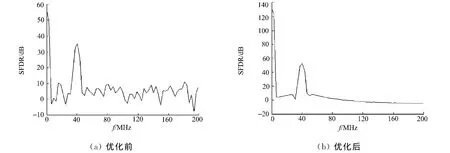
图5 数模转换器的SFDR仿真波形图Fig.5 SFDR simulation waveform of DAC

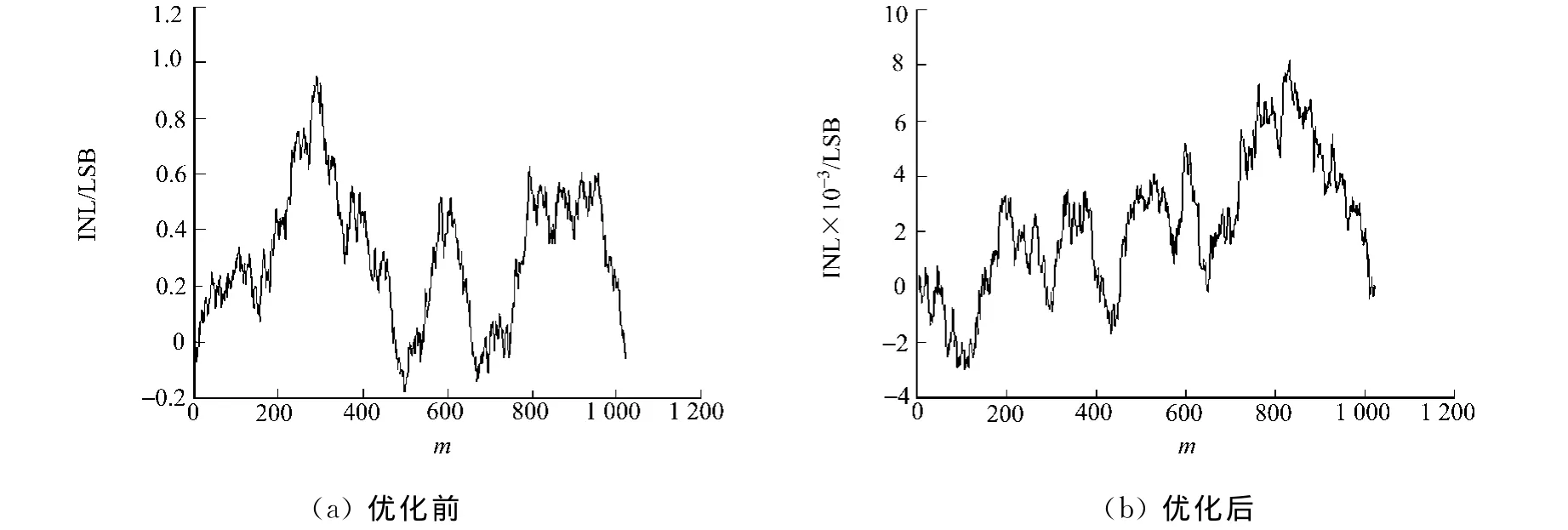
图6 数模转换器的积分非线性 Monte Carlo仿真Fig.6 INL Monte Carlo simulation for DAC

电流型数模转换器积分非线性的蒙特卡罗（Monte Carlo）仿真结果，如图6所示.图6仿真了20万个点，单位电流源的偏差为0%～0.1%，优化前后的仿真INLmax分别为0.9，0.008LSB.由于采用相同的初始条件进行Monte Carlo仿真测试，因此未优化前的积分非线性设计与Monte Carlo仿真结果有较大偏差（偏差500%），而优化后的模型测试表明积分非线性基本一致（偏差60%）.由式（13）可得优化模型具有较大的输出阻抗，面积越大，由尺寸失配引起的绝对误差和相对误差均大幅度减小，而且输出阻抗也显著增加，有利于减小因工作点失配而造成的误差，提高了蒙特卡罗仿真精度和准确度.

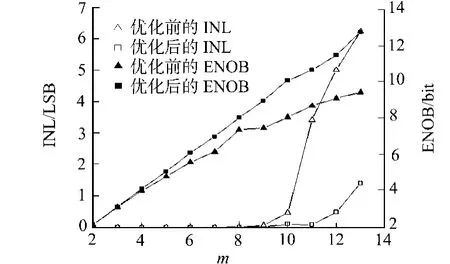
图7 综合仿真Fig.7 Integrated simulation

优化前后电流型数模转换器的积分非线性与有效位数的综合仿真结果，如图7所示.从图7可知，当温度计编码的电流源增加时，转换器的积分非线性增加；当温度计编码小于3bit时，未优化的积分非线性小于优化后的积分非线性；当温度计码大于3bit，未优化的电流源积分非线性增加的幅度远大于优化后的电路.与此同时，有效位数随着温度计编码的增加而增大，电流源数目越大，优化前后数模转换器的有效位数偏差也越大.

4 结束语

文中提出一种新型积分非线性优化方法，在M3和M4基础上增加M7和M10的差分互补开关减少毛刺现象.在此基础上，进行了计算机实验仿真，结果表明，优化后的积分非线性INLmax＝0.004 8LSB，线性度比优化前提高了37.5倍，SFDR提高了15dB，ENOB提高了2.116 3bit.同时，Monte Carlo仿真测试表明，未优化前的积分非线性设计与Monte Carlo仿真结果有500%的偏差，而优化后的结果测试表明积分非线性偏差仅为60%.

［1］SCHOFIELD W，MERCER D，ONGE L S.A 16b400MS／s DAC with＜－80dBc IMD to 300MHz and＜－160 dBm／Hz noise power spectral density［C］∥IEEE International Solid－State Circuits Conference Digest of Technical Papers.San Francisco：IEEE，2003：126－127.

［2］凌朝东，黄群峰，张艳红，等 .脑电信号提取专用电极芯片的设计［J］.华侨大学学报：自然科学版，2007，28（3）：260－263.

［3］MERCER D A.Low－power approaches to high－speed current－steering digital－to－analog converters in 0.18－μm CMOS［J］.IEEE J Solid－State Circuits，2007，42（8）：1688－1698.

［4］LU C W，HUANG L C.A 10－bit LCD column driver with piece wise linear digital－to－analog converters［J］.IEEE J Solid－State Circuits，2008，43（2）：371－378.

［5］JEON Y J，HYUNG M，LEE S W，et al.A piecewise－linear 10bit DAC architecture with drain current modulation for compact AMLCD driver ICs［C］∥IEEE International Solid－State Circuits Conference Digest of Technical Papers.San Francisco：IEEE，2009：264－265.

［6］VAN DEN BOSCH A，STEUAERT M，SANSEN W.An accurate statistical yield model for CMOS current－steering D／A converters［C］∥IEEE International Symposium on Circuits and Systems.Geneva：IEEE，2000：105－108.

［7］ALBIOL M，GONZALEZ J L，ALARCON E.Mismatch and dynamic modeling of current sources in current－steering CMOS D／A converters：An extended design procedure［J］.IEEE Transaction on Circuits and System，2004，51（1）：59－169.

［8］LIN C H，VAN DER GOES F，WESTRA J R，et al.A 12bit 2.9GS／s DAC with IM3＜－60dBc beyond 1GHz in 65nm CMOS［J］.IEEE J Solid－State Circuits，2009，44（12）：285－3293.

［9］GUBNER J A.Probability and random processes for electrical engineer［M］.Madison：University of Wisconsin－Madison，1993.

A Linear Optimization Method for Integral Non－Linearity Error and Its Application to Current－Mode Digital－to－Analog Converter

FU Wen－yuan1，2，LING Chao－dong1，2

（1.College of Information Science and Engineering，Huaqiao University，Quanzhou 362021，China；2.Key Laboratory of ASIC System，Xiamen 361008，China）

A novel integral nonlinear optimization method which is that added respectively in parallel two sets of auxiliary pseudo－differential cascode MOS transistor to the current source is presented.Auxiliary pseudo－differential cascode current source generates a negative signal with the original source of the opposite current integral nonlinearity error，which greatly reduce the digital－to－analog converter′s integral nonlinearity（INL）and switching glitches phenomenon.Simulation results show that INL decrease 96%，and effective number of bits（ENOB）increase 2.1bit，and spurious free dynamic range（SFDR）increase 15dB.Integral nonlinearity deviation is 500%compared to the results of the Monte Carlo simulation before the optimized，and it is reduced to 60%after the optimized design.

digital－to－analog converter；current mode；integral nonlinearity；current source

陈志贤 英文审校：吴逢铁）

TN 792

A

1000－5013（2012）02－0163－05

2011－02－25

傅文渊（1982－），男，助教，主要从事模拟集成电路的研究.E－mail：fwy＠hqu.edu.cn.

国家自然科学基金资助项目（60772164）；福建省自然科学基金资助项目（T0850005）