MIMO－OFDM系统中的时变信道均衡

陈东华

（华侨大学 信息科学与工程学院，福建 厦门 361021）

MIMO－OFDM系统中的时变信道均衡

陈东华

（华侨大学 信息科学与工程学院，福建 厦门 361021）

为了改善多输入多输出－正交频分复用（MIMO－OFDM）时变信道均衡性能，将最小均方误差排序串行干扰抵消（MMSE－OSIC）均衡算法应用于降维MIMO－OFDM信号模型的符号检测 .该方法一方面利用OSIC来获得时变多普勒分集，另一方面利用降维信号模型来降低均衡复杂度.仿真结果表明：该方法以较低的复杂度代价有效提高了系统性能.

多输入多输出；正交频分复用；子载波间干扰；均衡

高速移动环境中，信道的时变会破坏正交频分复用（OFDM）子载波之间的正交性，导致子载波间干扰（ICI）并恶化系统性能［1］.针对时变信道中多输入多输出－正交频分复用（MIMO－OFDM）的ICI抑制，文献［2］提出了一种时域均衡算法，但该算法没有利用OFDM固有的频域处理优势，具有很高的计算复杂度；文献［3］提出了一种频域迭代部分ICI抵消算法，但性能损失较大，需要借助于信道编码加以补偿；文献［4］提出了降维干扰对消检测方案，但误差传播限制了该方案的性能提高.最小均方误差排序串行干扰抵消算法（MMSE－OSIC）是贝尔实验室垂直分层空时（V－BLAST）系统中一种有效的检测算法［5］.文献［6］将其应用于单天线OFDM系统中的ICI均衡，但该算法复杂度较高，限制了其在实际系统中的应用.文献［7－8］通过限制子载波间干扰范围，分别提出了基于检测前信干噪比和检测增益的降维简单排序检测算法.但上述排序检测算法在 MIMO－OFDM系统中无法应用 .这是因为 MIMOOFDM系统中各发射天线的子载波在接收信号中互相耦合在一起，无法得到算法赖以工作的排序参数.基于此，本文研究将MMSE－OSIC均衡算法应用于降维MIMO－OFDM信号模型的符号检测.

1 系统模型

假设MIMO－OFDM系统有M个发射天线和R个接收天线，每符号有N个子载波，则接收机的第r（r＝1，2，…，R）个接收天线上的频域接收信号［3］为

式（1）中：Yr＝［Yr（0），…，Yr（N－1）］T为接收天线r上的频域信号矢量；Xt＝［Xt（0），…，Xt（N－1）］T为发射天线t上的发送信号矢量；Wr为零均值、方差的频域叠加噪声矢量；Hr，t为收发天线对（r，t）之间的信道频域响应（CFR）矩阵，其第（k，u）个元素为 Hr，t（k，u）.

将R个接收天线的接收矢量表示为新的矢量形式，有

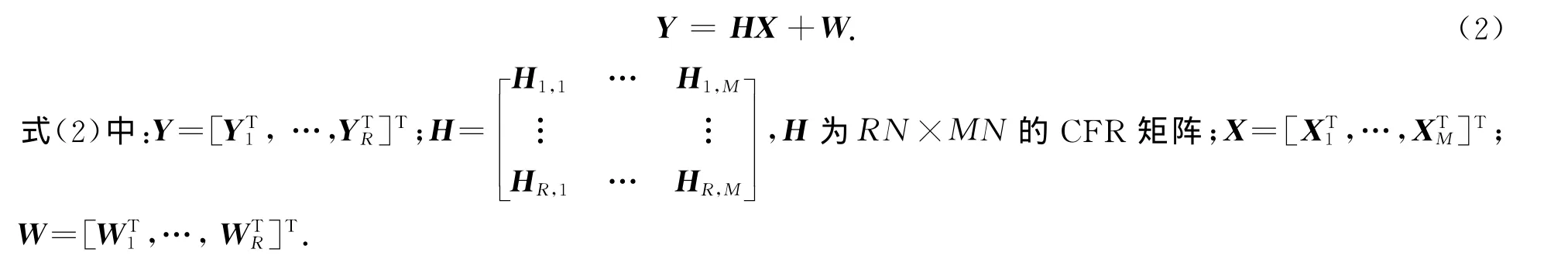
2 均衡算法

2.1 传统均衡算法

传统均衡算法采用线性最小均方误差（LMMSE）均衡器［6］，可表示为

式（3）中：IRN为RN×RN的单位阵.传统均衡算法考虑了所有ICI，需要RN×RN维矩阵求逆，因此具有很高的计算复杂度.为了降低计算复杂度并提高均衡性能，在降维信号模型的基础上应用排序SIC进行MIMO－OFDM的ICI均衡.

2.2 降维均衡算法

与文献［4，7－10］相同，假设考虑的子载波间干扰范围为2D＋1，对任意一对收发天线（r，t），第k个子载波Xt（k）的能量集中分布在2D＋1个接收子载波Yr（k）上 .定义Yr（k）为Yr（k）＝［Yr（k－D），…，Yr（k＋D）］T，忽略带外ICI，则Yr（k）可表示为

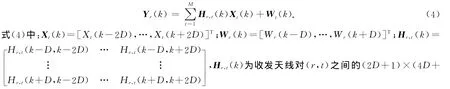
1）维部分CFR矩阵 .上述各式中有关子载波变量的运算均为模N运算.

将R个接收天线上的信号Yr（k）写成矢量形式，有

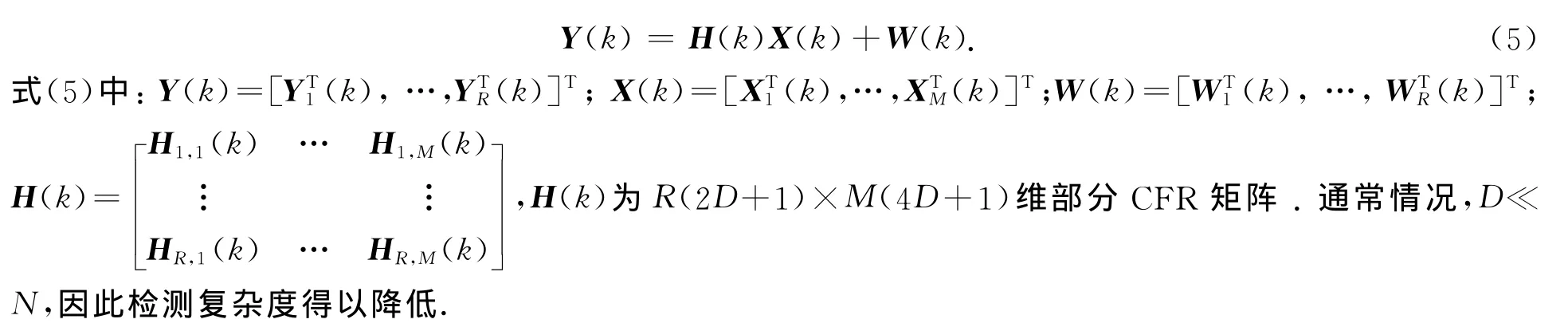
由式（5）可知，发射天线t上的子载波Xt（k）的LMMSE均衡矢量为

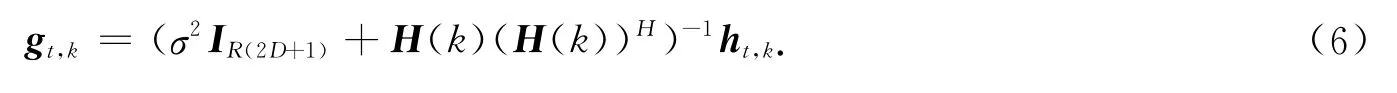
对应的LMMSE估计为

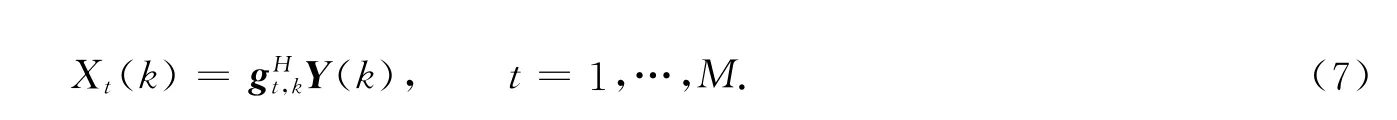
式（7）中：ht，k为H（k）的第（（t－1）（4D＋1）＋（2D＋1））列元素对应的列矢量.

2.3 降维排序SIC均衡算法

降维MMSE－SIC算法是MIMO－OFDM提高系统检测性能的有效手段［4］.记M副发射天线的第k个子载波矢量为XM（k）＝［X1（k），…，XM（k）］T.在得到其估计后，将产生的ICI从接收信号中减去［4，6-8］，即有

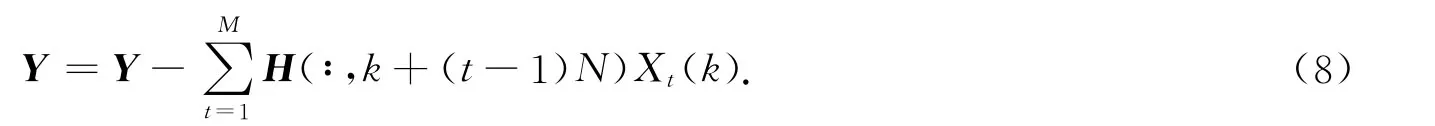
式（8）中：H（∶，k）表示H的第k列.同时，将XM（k）对其他子载波的ICI加权在H中消除，即将H的对应第k列置零.消除已检测子载波的ICI后，可得到新的接收信号矢量Y和对应的CFR矩阵H.按式（8）构造第（k＋1）个子载波矢量XM（k＋1）的接收信号模型，同第k个子载波组的检测过程相同，依次递归直到所有N个子载波组检测完毕.

MMSE－SIC算法采用的是判决反馈均衡思想，在判决反馈过程中错误的判决将引起差错传播 .排序方法是提高SIC检测可靠性的重要技术［6-8］，但传统单天线OFDM系统中的排序检测算法［7-8］在 MIMO－OFDM系统中不再适用 .这是由于在MIMO系统中，各发射天线的子载波在接收信号中互相耦合在一起，无法得到算法赖以工作的排序参数，而且在MIMO系统中，基于检测前信干噪比和检测增益的简单排序准则性能较差.针对这些问题，以式（5）为信号检测模型，首先计算各副发送天线上的子载波组检测后的信号功率与ICI和噪声功率之比（信干噪比，RSIN）的和，然后按信干噪比之和由大到小的顺序进行MMSE－OSIC检测 .由式（5）可得各副发送天线上的第k子载波组检测后的RSIN之和为

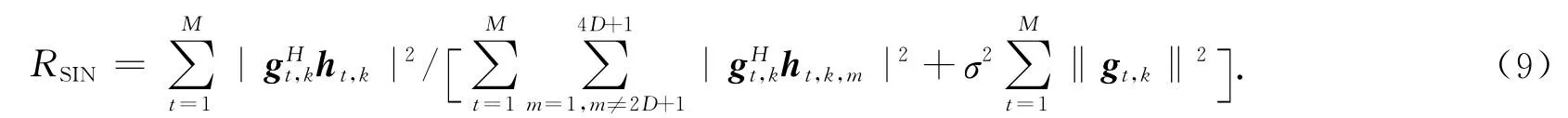
式（9）中：ht，k，m为H（k）的第（（t－1）（4D＋1）＋m）列.完整的检测过程有如下5个主要步骤 .

1）根据式（9）计算所有未检测子载波的RSIN，选取具有最大RSIN之和的子载波组（假设为第k组：XM（k）＝［X1（k），…，XM（k）］T）作为检测对象；

2）用式（6）构造相应的均衡器，用式（7）均衡出各发射天线上的子载波矢量XM（k）；

3）对XM（k）进行硬判决，判决结果仍定义为XM（k）；

4）从接收信号中减去XM（k）对其他子载波的ICI，并将H的第k＋（t－1）N （t＝1，…，M）列置零；

5）返回步骤1）～4），直到所有子载波检测完毕.

2.4 算法复杂度

首先，检测所有子载波需要N（N－1）／2次排序操作，每1次排序需要计算1次RSIN值，由式（9）可知，计算1次RSIN的复杂度为O（（DR）2M）.其次，检测所有子载波需要N次均衡，每次均衡的复杂度为O（（DR）3M）.最后，执行1次ICI抵消的复杂度为O（NRM），共需执行N－1次 .

因此，完整的算法复杂度为O（N2（DR）2M／2＋N（DR）3M＋N2RM），通常D≪N.由于利用了降维信号模型，使得间隔大于2D＋1的子载波之间的耦合得以解除，故降维排序检测算法具有较低的复杂度.

3 仿真分析

通过大量的蒙特卡洛模拟仿真，得到归一化（对子载波间隔）不同多普勒频率时系统的误比特率（RBE）性能，如图1所示.图1中的仿真参数：收发天线数R＝M＝2；OFDM系统采用QPSK调制，每符号子载波数N＝64，循环前缀长度为16，信道由4条等增益路径组成；参数D的选取取决于复杂度与性能的要求，当D较大时，系统性能较高，但复杂度随之增加；反之，当D较小时，复杂度降低，但系统性能也随之降低.此外，图1中“Full MMSE”和“降维 MMSE”分别对应式（3），（6）；“降维 MMSE－SIC”、“降维MMSE－OSIC”分别在式（6）基础上增加干扰抵消和文中的排序干扰抵消.

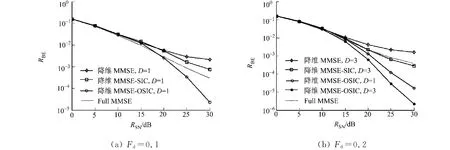
图1 系统误比特率性能的仿真结果Fig.1 System performance in terms of bit error rate obtained from simulations

由图1可见，由于考虑的子载波间隔较小，降维LMMSE均衡算法性能较差，通过SIC可获得一定的性能增益，而初始检测的可靠性较低，在SIC过程中存在误差传播，性能仍不理想 .式（3）表达的全MMSE均衡器（非降维）考虑了所有的子载波，能同时抑制载波间干扰与共信道干扰，但其性能提高有限且实现复杂度很高；降维排序SIC算法可获得比全MMSE均衡算法更好的性能，即在每次检测过程当中，算法都能保证当前所检测子载波具有最高的检测可靠性，使得SIC误差传播概率降为最小.

此外，虽然信道的时变导致ICI，但另一方面，由于某一发射子载波的能量分散在各接收子载波上，意味着信道的时变带来了时间分集作用，排序算法在串行检测过程中通过逐步抵消ICI，使得降维LMMSE均衡器能充分利用时间分集效应 .当信道变化较快时（Fd由0.1增至0.2），这种分集带来的性能增益尤为明显.全LMMSE均衡器虽然考虑了所有ICI，但在严重的子载波间干扰下，时间分集效应得不到有效利用，因此降维排序算法能获得比全LMMSE均衡器更好的性能.

4 结束语

MIMO－OFDM时变信道均衡算法的性能与复杂度是实际应用中必须考虑的问题 .文中主要研究了基于降维信号模型的排序均衡方案，该方案能充分利用信道时变带来的时间分集增益，有效提高了系统性能，并且具有较低的实现复杂度，便于实时应用.

［1］JIANG Q，SPEIDEL J，ZHAO C.A joint OFDM channel estimation and ICI cancellation for double selective channels［J］.Wireless Personal Communalizations，2008，45（1）：131－143.

［2］STAMOULIS A，DIGGAVI S N，Al－DHAHIR N.Intercarrier interference in MIMO－OFDM［J］.IEEE Transactions on Signal Processing，2002，50（10）：2451－2464.

［3］张阳，李建东，李维英，等.MIMO－OFDM系统中的子载波间干扰消除［J］.西安电子科技大学学报，2009，36（9）：761－766.

［4］俞菲，杨绿溪.MIMO－OFDM 快时变信道下的一种低复杂度的检测算法［J］.电子与信息学报，2007，29（7）：1584－1587.

［6］GOLDEN G D，FOSCHINI C J，VALENZUELA R A，et al.Detection algorithm and initial laboratory results using V－BLAST space－time communication architecture［J］.Electronics Letters，1999，35（1）：6－7.

［7］CHOI Y S，VOLTZ P J，CASSARA F A.On channel estimation and detection for multicarrier signals in fast and selective Rayleigh fading channels［J］.IEEE Transactions on Communications，2001，49（8）：1375–1387.

［8］WANG H，CHEN X，ZHOU S，et al.Low－complexity ICI cancellation in frequency domain for OFDM systems in time－varying multipath channels［J］.IEICE Transactions on Communications，2006，89（3）：1020－1023.

［9］KIM K，PARK H.A low complexity ICI cancellation method for high mobility OFDM systems［C］∥IEEE Vehicular Technology Conference.Montréal：IEEE，2006：2528－2532.

［10］LU S，Al－DHAHIR N.Coherent and differential ICI cancellation for mobile OFDM with application to DVB－H［J］.IEEE Transactions on Wireless Communications，2008，7（11）：4110－4116.

［11］HWANG S U，LEE J H，SEO J.Low complexity iterative ICI cancellation and equalization for OFDM systems over doubly selective channels［J］.IEEE Transactions on Broadcasting，2009，55（1）：132－139.

Equalization of Time－Varying Channels for MIMO－OFDM Systems

CHEN Dong－hua
（College of Information Science and Engineering，Huaqiao University，Xiamen 361021，China）

In order to improve the equalization performance of multiple input multiple output／orthogonal frequency division multiplexing（MIMO－OFDM）system in time varying channels，the minimum mean squared error equalization scheme with sorted successive interference cancellation（MMSE－OSIC）is used to detect the transmitted symbols relying on a reduced signal model，and as a result，the Doppler diversity caused by channel time variation is thus exploited by the OSIC，and moreover，the computational complexity of this method is reduced by using the reduced signal model.Theoretical analysis and simulation results show that this method improves the performance of MIMO－OFDM system in time－varying channels with a low cost of computational complexity.

multiple input multiple output；orthogonal frequency division multiplexing；intercarrier interference；equalizer

钱筠 英文审校：吴逢铁）

TN 911.5

A

1000－5013（2012）02－0149－04

2011－03－21

陈东华（1977－），男，讲师，主要从事宽带通信的研究.E－mail：dhchen＠hqu.edu.cn.

华侨大学科研基金资助项目（07HZR26）