部分二次特征值及其敏感性配置

谢溪庄

（华侨大学 数学科学学院，福建 泉州 362021）

部分二次特征值及其敏感性配置

谢溪庄

（华侨大学 数学科学学院，福建 泉州 362021）

利用响应矩阵法配置主动振动控制中的配置特征值及其敏感性，使得特征值和敏感性配置的个数不受限制.提出用带等式约束的二次规划问题，来求解主动振动控制中单输入状态反馈控制系统的部分特征值及敏感性配置问题.数值实验表明：转化成二次规划问题来求解的方法，其特征值配置问题满足要求，敏感性配置也相对满足要求.

特征值；敏感性；二次规划问题；响应矩阵法；主动振动控制

在结构动力学中，许多反特征值问题中都要求系统有特征值的敏感性.例如，在主动振动控制中不仅要求通过引入某种控制器，使得部分系统的特征值可以移动到指定的位置，从而使系统的动态性能得到改善，而且要使特征值的敏感性达到一定的要求.Ram等［1］提出了用响应矩阵法解决主动振动控制中的特征值配置问题.对于主动振动控制中单输入状态反馈控制系统的部分特征值及敏感性配置问题［2］，Mottershead等［3］提出可以将特征值及其敏感性配置转化成线性方程，并通过解线性方程组的方式来解决问题.然而，当方程组为超定方程组时，可能出现无解的情况.因此，本文中提出用带等式约束的二次规划问题来求解.

1 响应矩阵法

首先考虑二阶矩阵微分方程为

式（1）中：M，C，K是n×n实对称阵，M 是正定的，C，K 是半正定的.通过变量分离z（t）＝xeλt，其中λ∈x，x∈xn是一个常向量.由此可得

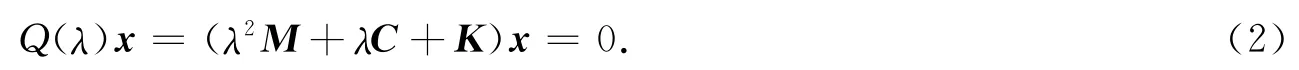
记Q（λ）＝λ2M＋λC＋K，矩阵多项式Q（λ）称为开环二次束，（λ，x）称为Q（λ）的特征对.

开环的响应矩阵的形式如下

也可以把它表示成如下形式，即

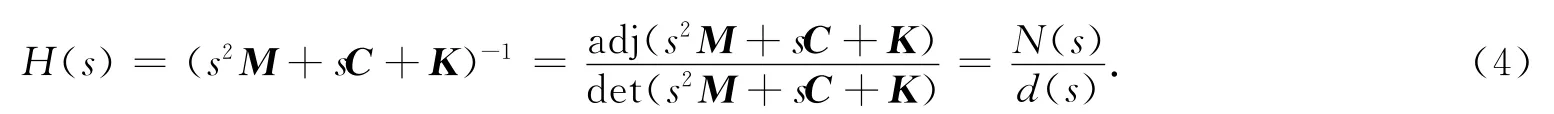
式（4）中：adj A为矩阵A的伴随矩阵；det A为矩阵A的行列式.

2 响应矩阵法配置主动振动控制的特征值及其敏感性

考虑单输入状态反馈主动振动控制系统为

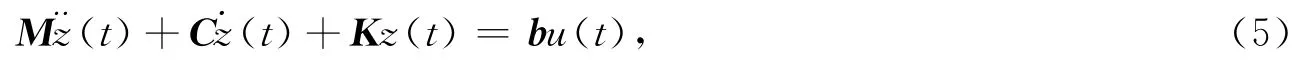
其中：b，f，g∈Rn.

结合式（5），（6）及变量分离z（t）＝xeλt，有

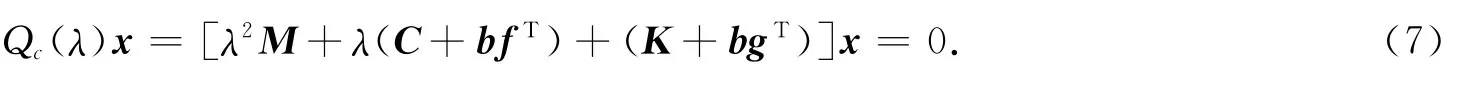
式（7）中：Qc（λ）＝［λ2M＋λ（C＋bfT）＋（K＋bgT）］为闭环二次束.

由Sherman－Amorrison式

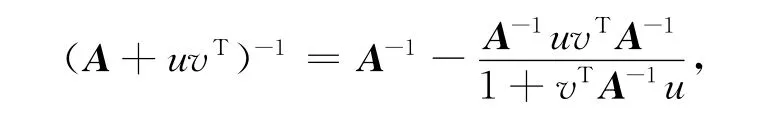
可得闭环的响应矩阵为

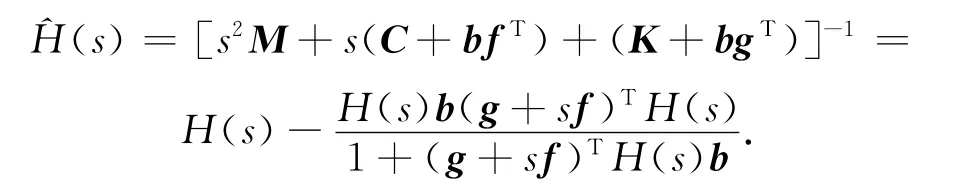
部分特征值配置问题就是给定 M，C，K∈Rn×n，向量b∈Rn，集合L＝｛μ1，μ2，…，μp｝，满足当μj∈L时，¯μj∈L且｛μ1，μ2，…，μp｝∩｛λ1，λ2，…，λ2n｝＝Ø，其中λi为Q（λ）的特征值.求得f，g∈Rn，使得｛μ1，μ2，…，μp｝为Qc（λ）的p个特征值.

若｛μ1，μ2，…，μp｝为Qc（λ）的p个特征值，由文献［3］可知

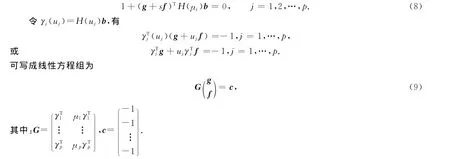
由式（9）可知，当L＝｛μ1，μ2，…，μp｝满足μj∈L，¯μj∈L时，f和g是实向量，且当p＜2n时，线性方程组（9）有无数多个解.另外，由文献［3］可以得到特征值关于向量g的敏感性为

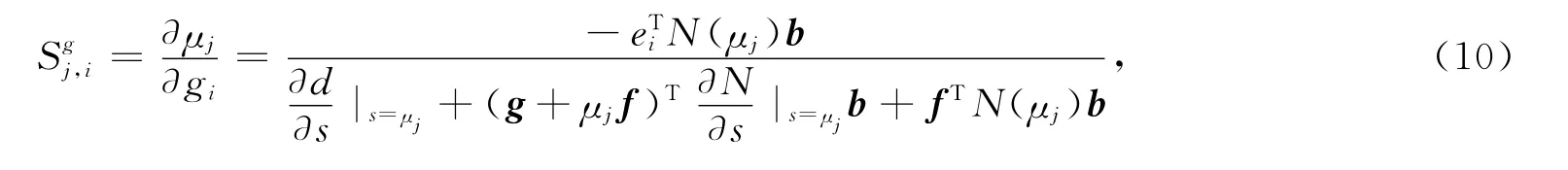
特征值关于向量f敏感性为

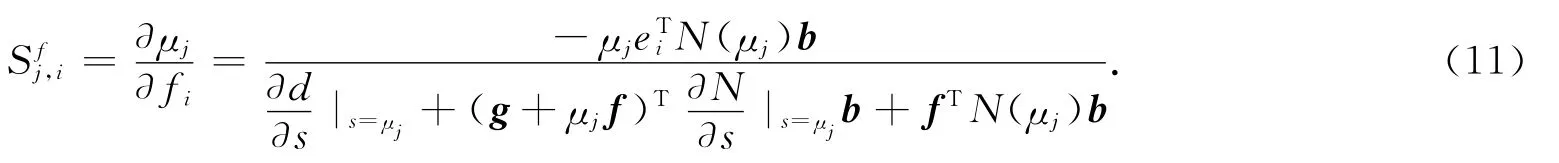
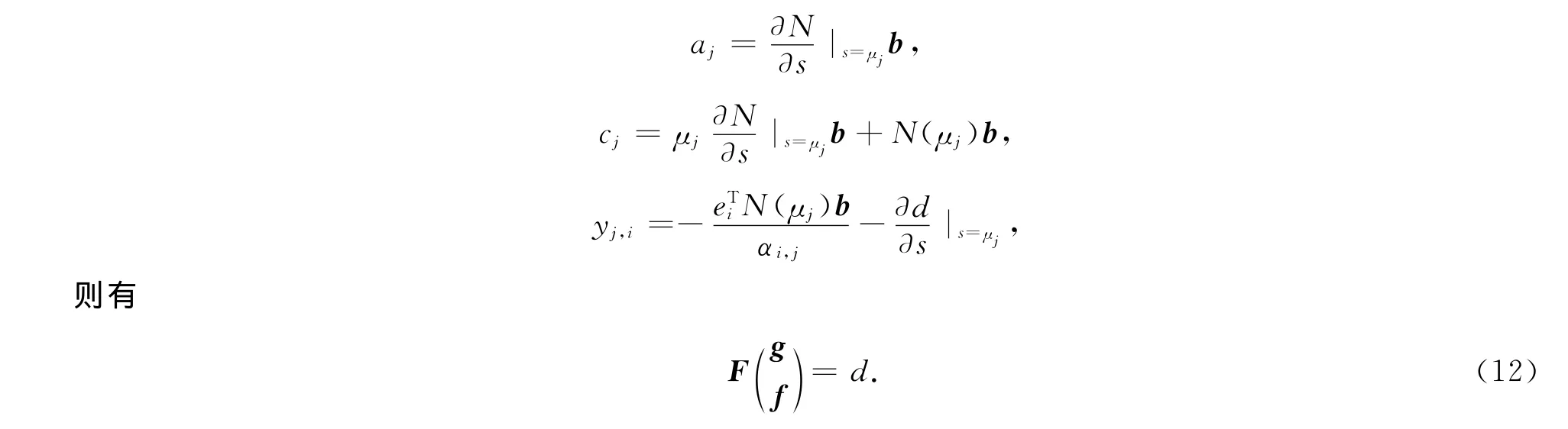
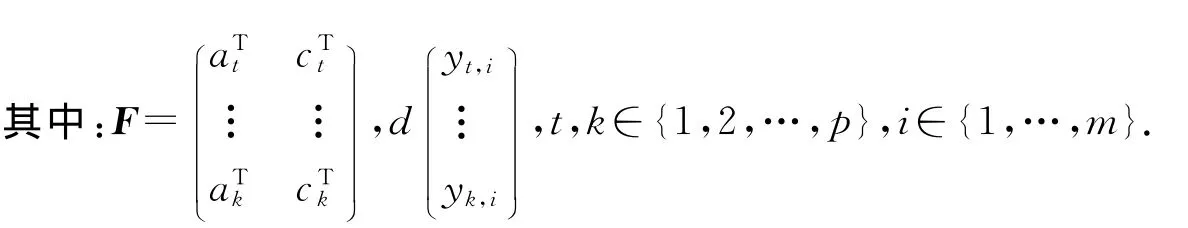
3 带等式约束的二次规划问题

对特征值的配置与对其敏感性的配置都可以转化成求解关于f和g的线性方程组.令u＝（gTfT）T，要对两者同时进行配置时，结合式（9）和式（12）可以求解下面的二次规划问题［4］，即

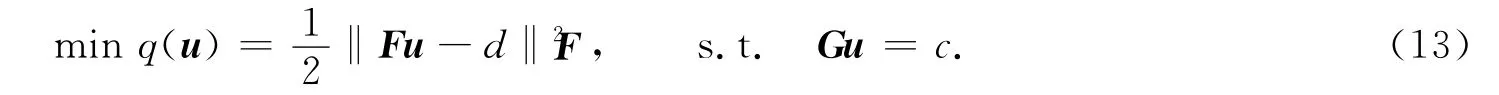
其中：‖·‖F为F－范数.

当F，G是满秩矩阵时，q（u）是强凸函数，Ω＝｛u∈R2n｜Gu＝c｝是一个闭凸集，二次规划问题（13）有唯一解，且等价于求解下面的线性方程组，即

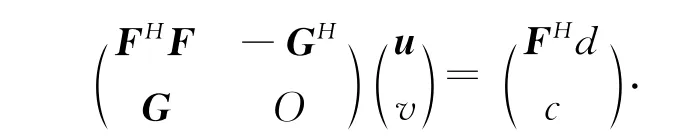
其中：FH为f的共轭转置阵［5］.

Mottershead等［3］提出通过下面的线性方程组来求解g和f，即

注1 当F，G不是满秩矩阵时，可以先将线性方程组（14）的系数矩阵进行QR分解，提取其中满秩的部分，建立新的二次规划问题进行求解.

4 数值实验

设M，C，K，b具有下面的形式，即

其开环的特征值为λ1，2＝－0.016 6±0.551 6i，λ3，4＝－0.252 8±2.228 9i，λ5，6＝－0.252 8±2.228 9i.

例1 将前面4个开环特征值λ1，2，λ3，4替换为u1，2＝－0.02±0.8i，u3，4＝－0.3±1.9i，给定u3，4＝－0.3±1.9i，相对于g的第1个分量的敏感性为.可求解下面的线性方程组（14），得唯一解为

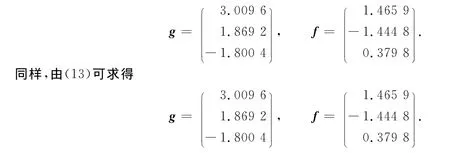
其相应的闭环特征值为u1，2＝－0.02±0.8i，u3，4＝－0.3±1.9i，u5，6＝0.154 3±2.560 1i且u3，4的敏感性.

从上面的实验可以看出，在例1中，式（13）与式（14）的解是相同的.此时式（13）的目标函数q（u）＝1.46×10－6（其值不为0是由于计算机的计算误差）.

例2 在例1的基础上，再给定u1，2＝－0.02±0.8i，相对g的第1个分量的敏感性为.显然，这种情况下线性方程组（14）是一个超定方程组，无解.只能求解二次规划问题（13）且可解得

其闭环特征值为u1，2＝－0.02±0.8i，u3，4＝－0.3±1.9i，u5，6＝－0.037 2±2.431 6i；而其相应的敏感性为＝－0.05＋0.133 5i，＝－0.05－0.133 5i，＝－0.018 4－0.124 9i，＝－0.018 4－0.124 9i.

由此可以看到特征值配置问题满足要求，敏感性配置虽不是为给定的值，也是比较相对满足要求的.此时，式（13）的目标函数q（u）＝5.06×104.

［1］RAM Y M，MOTTERSHEAD J E.Receptance metheod in active vibration control［J］.AIAA Journal，2007，45（3）：562－567.

［2］龚德恩.利用矩阵广义逆的极点配置问题新解法［J］.华侨大学学报：自然科学版，2000，21（1）：101－106.

［3］MOTTERSHEAD J E，TEHRANI M G，RAM Y M.Assignment of eigenvalue sensitivities from receptance measurements［J］.Mechanical Systems and Signal Processing，2009，23（6）：1931－1939.

［4］BERTSEKAS D P.凸分析与优化［M］.北京：清华大学出版社，2007.

［5］NOCEDAL J，WRIGHT S J.Numerical optimization［J］.2nd ed.Berlin：Springer－Verlag，2006.

Assignment of Eigenvalue and Corresponding Sensitivities

XIE Xi－zhuang
（School of Mathematical Sciences，Huaqiao University，Quanzhou 362021，China）

By means of assignment for the eigenvalue and the corresponding sensitivities in active vibration control by receptance method，the number of the assigned eigenvalue and sensitivities isn′t limited.We present an equality－constrained quadratic programming method to solve the problem of eigenvalue and sensitivities assignment in active vibration control using single－input state feedback.It is shown that the eigenvalue and sensitivities can be assigned by the quadratic programming method by numerical tests.

eigenvalue assignment；sensitivity；quadratic programming；receptance method；active vibration control

黄晓楠 英文审校：张金顺，黄心中）

O 231.1

A

1000－5013（2012）01－0117－04

2011－05－22

谢溪庄 （1981－），男，助教，主要从事应用数学的研究.E－mail：xzx＠hqu.edu.cn.

国务院侨办科研基金资助项目（09QZR10）