狄拉克函数δ(f)的作用

李泽光

（大连大学 信息工程学院, 辽宁 大连 116622）

狄拉克函数δ(f)的作用

李泽光

（大连大学 信息工程学院, 辽宁 大连 116622）

狄拉克函数δ(f)被广泛用在信号的傅立叶变换中，但是这个函数的作用一直是人们最关心的问题，本文通过余弦信号的傅立叶级数和傅立叶变换的分析揭示了δ(f)函数在函数中的物理意义和作用，它是自变量定位函数，另外还揭示复指数函数表示信号频谱的意义和优点。

狄拉克函数；傅立叶变换；频谱；自变量定位函数

δ(f)函数被广泛用在信号的傅立叶变换中，但是这个函数在函数表示中的作用一直是人们最关心的问题，本文通过余弦信号（这里以余弦函数作基准，通常将正弦函数和余弦函数统称为“正弦函数”）的傅立叶级数和傅立叶变换分析最终揭示了δ(f)函数的物理意义和它的作用。

1 δ(f)的定义及性质

δ(f)函数的定义在许多参考文献中都有详细说明，这里对δ(f)函数只做简单介绍。如图1所示，当Δ→0时，函数p△( f)的宽度趋于零，而函数的幅度趋于无限大，但其强度仍为1（脉冲面积为1），这个函数就定义为单位冲激函数（或称为狄拉克函数）用δ(f)表示，如图2所示，即

图1 窄脉冲

图2 δ(f)函数

狄拉克（Dirac）给出了冲激函数另一种定义，即

说明δ(f)或δ(f-f0)函数只在一点有定义，另外，如果f表示信号频率，而角频率ω=2π f，则有

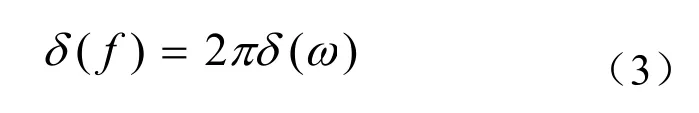
也就是说，如果用ω做自变量（坐标横轴用ω），ω坐标轴相当于比f坐标轴压缩2π倍，那么冲激函数δ( )ω的冲激强度要乘以2π。下面通过余弦信号的傅立叶级数以及余弦信号的傅立叶变换分析来揭示δ(f)的物理意义和它的作用。

2 余弦信号及三参数

若自变量为时间t，则余弦信号的数学表达式写成：

式中c1为信号幅度（峰值），φ1为初相位，ω1为角频率；角频率ω1与频率f1以及周期T1的关系为ω1=2πf1=2π/T1。对于余弦信号来说，如果知道幅度c1、初相位φ1和角频率ω1（或频率f1）这“三个参数”，则就知道这个余弦信号的“全部信息”了。

3 余弦信号的傅立叶级数及频谱

我们知道，周期信号x(t)的三角函数形式的傅立叶级数为：

余弦信号也是周期信号，它也可以写成三角函数形式傅立叶级数，对于式（4）表示的单一频率的余弦信号，从（5）式中得到：

余弦信号x( t)=c1cos(ω1t+φ1)只有一个频率f1，在频率轴从0 HZ到∞范围内找到这个频率点f1，以幅度和初相位为纵坐标分别画出这个余弦信号的幅度谱线和相位谱线，其中φ1≤π,如图3和图4分别表示三角函数形式的傅立叶级数的余弦信号幅度谱和相位谱，从图3和图4中可以得到余弦信号的“三参数”。

图3 余弦信号的幅度谱线

图4 余弦信号的相位谱线

如果信号x( t)含有多个频率成分（不同频率的余弦信号的叠加），则信号x( t)的频谱就是将组成这个信号的所有不同频率的余弦信号的“三参数”表示出来，周期信号的三角函数形式的傅立叶级数的频谱是将其中的每个频率的余弦信号的三个参数（幅度、初相和频率或角频率）都各自分别表示出来。

另外，傅立叶级数还有指数形式，下面我们就看看用指数形式表示有什么好处。

周期信号指数形式的傅立叶级数形式为：

可以看到，用指数形式表示的好处是，每个余弦信号的“三参数”中的幅度和初相位都包含在Fn中，但这里却出现了负频率的问题，Fn的绝对值Fn只有余弦信号幅度Cn的一半，另外一半放在负频率处了，也就是，为了将余弦信号的幅度和初相位都放在复指数Fn中一起表示，则带来的后果就是在数学中就出现了负频率，将实际余弦信号的幅度和相位分别放在正、负频率处。用Fn表示的频谱如图5和图6所示。

图5 指数形式的幅度谱

图6 指数形式的相位谱

4 从余弦信号的傅立叶变换中看δ(f)函数的作用

将余弦信号写成指数形式

信号的傅立叶变换实际上是给出了组成这个信号的所有频率（或角频率）的余弦信号的“三参数”的全部信息,而这些信息用傅立叶变换函数形式给出，从式（13）可以看到，式中除了含有频率为f1的余弦信号的幅度和初相位之外，还利用δ(f-f1)和δ(f+f1)函数分别表示了正、负频率点f1和-f1，相应的表达式ejφ1δ(f-f1)就相当于三参数：、φ1和f1。所以，δ(f)在函数中起到了自变量定位作用，用δ(f)函数的形式来表示某一个自变量点。同样，狄拉克函数在时域表示信号时也是用此函数的形式表示某个时间点。在函数中可以将狄拉克函数称为自变量定位函数。

从频谱表示上看，信号傅立叶变换即式（12）和式（13）的相位谱都是如图7所示，但是，幅度谱出现了偏差，这是因为傅立叶变换中的幅度谱用到了δ(f)函数的原因，从（3）式中可知，用角频率ω作自变量和用频率f作自变量，δ(ω)和δ(f)要差系数2π；图5中傅立叶指数形式的中没有出现δ(f)函数，所以，图5中横坐标用角频率ω还是用频率f，幅度谱图没有区别。傅立叶变换的幅度谱分别用图8和图9表示。对于余弦信号的幅度谱来说，图3、图5和图9是一致的，而图8与其它频谱图相差了系数2π。既然，同一个余弦信号的傅立叶级数和傅立叶变换都是表示同一个余弦信号的“三参数”，因此，图3、图5、图9和图8的幅度谱是统一的，物理意义是相同的。而它们的区别在于，三角函数形式的傅立叶级数的频谱是将原信号含有的所有频率的余弦信号的“三参数”各自给出；指数形式的傅立叶级数的频谱是将原信号含有的所有频率的余弦信号的“三参数”中的幅度和相位一起放在复指数Fn中一起给出，频率点单独给出；而周期信号的傅立叶变换是将原信号含有的所有频率的余弦信号的“三参数”用这个“傅立叶变换函数”式形式一起给出的，其中频率点用自变量定位函数表示。

图7 余弦信号的相位谱

图8 余弦信号的幅度谱

图9 余弦信号的幅度谱

5 结论

通过对余弦信号傅立叶级数和傅立叶变换的分析以及余弦信号频谱分析，不但揭示了信号频谱的物理意义，更重要的是揭示了δ(f)函数在其它函数中的作用，即用狄拉克函数形式表示一个函数自变量的某个点，所以，可以将狄拉克函数称为其它函数的“自变量定位函数”，知道δ(f)函数的意义和作用对揭示一般函数的表示具有重要意义。

[1] 李泽光. 傅立叶变换信号系统学意义[J]. 大连大学学报, 2009(6): 60-64.

[2] 郑君里, 应启珩, 杨为理. 信号与系统[M]. 第2版.北京: 高等教育出版社, 2000.

[3] 吴大正. 信号与线性系统分析[M]. 第4版. 北京: 高等教育出版社, 2005.

Function of Dirac Function δ(f)

LIZe-guang

(College of Information Engineering, Dalian University, Dalian 116622, China)

Dirac function is widely used in Fourier transform, but the function of Dirac function is more concerned with people. The physical meaning and function of Dirac function are revealed by analysis of Fourier series and Fourier transform of cosine signal. It is an independent variable locating function. Besides, the meaning and advantage of signal spectrum expressed by complex exponent function expressing are presented.

dirac functionδ(f); fourier transform; spectrum; independent variable locating function.

TN911.7

A

1008-2395(2012)03-0014-03

2011-12-23

李泽光（1963-），男，教授，研究方向：信息与信号处理。