考虑潮流水平变化的电网二级连锁过载中的涨落现象研究
2012-12-26邓慧琼苏爱宁孙克军
邓慧琼,苏爱宁,孙克军
(河北科技大学电气工程学院,河北石家庄 050018)
考虑潮流水平变化的电网二级连锁过载中的涨落现象研究
邓慧琼,苏爱宁,孙克军
(河北科技大学电气工程学院,河北石家庄 050018)
针对电网的二级连锁过载模式,从网络保持结构完整性的角度,研究了潮流水平的变化所引起的涨落现象。首先依据支路因连锁过载开断而削弱电网的基本思路,定义了一种反映网络保持结构完整性的统计涨落模型,然后以IEEE 39节点系统为例,通过连续增加电网节点注入功率的方式,研究了电网在初始故障作用下发生连锁过载的涨落变化规律。分析表明,在电网二级连锁过载事件中,随着系统总的有功负荷的提高,相关物理量的涨落变化总体呈上升趋势,而且存在着比较明显的涨落放大的临界点。最后通过IEEE 14节点系统上的算例对此规律做进一步的验证。
电力系统;连锁故障;连锁过载;潮流水平;涨落
历史统计表明,在停电事故的早期一般存在因潮流转移导致的连锁过载过程,所以连锁过载是电网连锁故障中比较重要的一类形式,而且得到了较为普遍的重视[1]。
对于电力系统这样的复杂系统,某一初始故障发生后是否能引发连锁过载以及某一连锁过载发生后所表现出来的后果,不仅和初始故障的位置等因素有关,而且还和系统的运行状态密切相关[2]。从而在具体的运行状态下针对任一特定的初始故障往往只能给出一些具体的连锁过载发展模式,却不能给出一些宏观的统计信息。
对此,为了挖掘一些统计规律以便为进一步的研究提供借鉴,笔者针对二级连锁过载,从电网能否保持结构完整性的角度,给出了多个不同初始故障作用后所引起的网络完整性变化的统计模型,并利用该统计模型中能反映涨落的主要特征参量——统计离散度,以IEEE 39节点系统为例,对不同潮流水平下的涨落现象以及一些相关的规律进行了分析研究,并进一步采用IEEE 14节点系统和IEEE 57节点系统,按照同样的计算分析思路进行了验证。
1 基本模型
在统计物理学当中,涨落指的是物理量在平衡态附近的波动现象,它对系统结构的演化起着重要的作用[3]。引起涨落的原因可以是来自内部或外部的各种扰动。
对于电力系统而言,当考虑系统的运行状态和故障2类因素时,在连锁过载模式下,运行状态的变化和初始故障的作用有可能使得电网的结构形态发生波动。
为了进一步量化分析,主要考虑如下的场景:设在某一运行状态R1下,电网有n条支路分别发生初始故障。在每一初始故障支路被切除后,电网可能因潮流转移而发生连锁过载,并发生新的开断,设此时电网未被开断的支路数量为X。将上述n条支路分别作为初始故障,通过模拟计算分析完毕以后,则可以得到数量为n的一组样本数据X1,X2,…,X n,其中,X1代表第1条支路发生初始故障后电网中未被开断的支路数量,X2代表第2条支路发生初始故障后电网中未被开断的支路数量,其余类推。根据这一组样本数据,则可以得到在这一组初始故障作用下,电网未被开断的支路数量的统计均值,记为x R1,其下标R1表示该统计均值是在R1状态下得到的,即

式中,<X>表示X的均值。上述连锁过载分析,只考虑了初始故障发生和初始故障被切除后因潮流转移引起的新一轮过载开断现象,所以称之为二级连锁过载。以下均围绕此模式展开讨论。在得到式(1)所示的均值后,还可以进一步得到该组数据的样本方差:

上述式(1)-式(3)所定义的各个变量是在同一运行状态下R1求得的。这里,可假设这样一种情形:如果在计算这些变量时,电网的运行状态并非R1,而是R2,那么按照同样的计算方法得到的x R2,sR2,σR2的值就有可能和x R1,sR1,σR1的值不同,则σ值的波动反映了电网在同一组初始扰动故障作用下,其潮流状态所产生的影响。
2 分析流程
按照上述基本思路,对于一个具体的电网,为了研究在某些初始故障的作用下,电网潮流状态对σ值的影响规律,主要按照不断改变电网注入功率,在不同的潮流状态下分别模拟计算的思路进行分析,具体流程如图1所示。
对于图1中改变节点注入功率的方式,采用式(4)的形式:

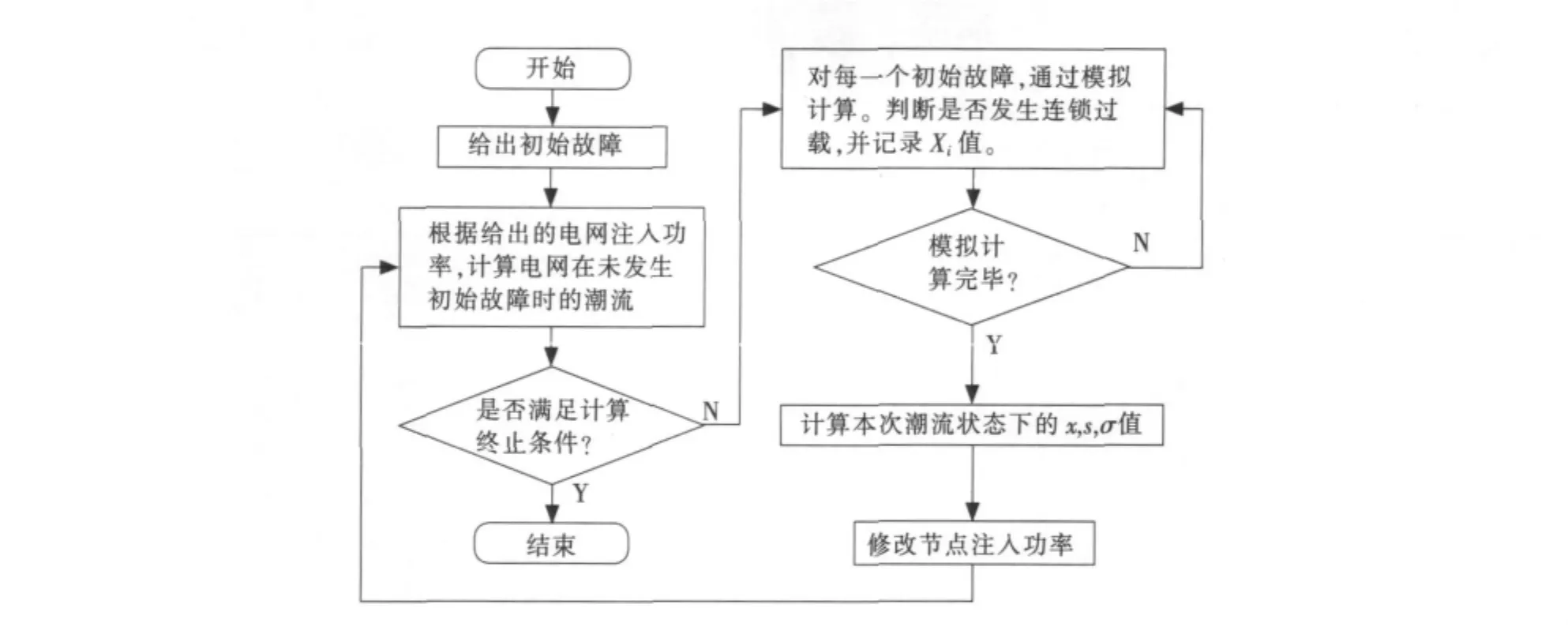
图1 分析流程图Fig.1 Flow diagram of analysis
式中,PGi(j),P Li(j)和QLi(j)分别为节点i在第j次计算时的有功功率、有功负荷和无功负荷。λj为第j次计算时的节点功率增加比例,前后2次计算中的λ增量Δλ取为大于零,即将节点注入功率以逐渐增加的方式进行,计算终止的条件是直到潮流不收敛为止,因这时电网运行状态已接近电压稳定极限。
3 IEEE 39节点系统上的分析
为了得到一些规律性的认识,这里先采用IEEE 39节点系统进行计算分析,系统的接线图如图2所示。在计算中,主要考虑了以下原则。
1)初始故障发生前的潮流和支路开断模拟均通过调用电力系统分析软件BPA来完成。
2)连锁过载主要考虑功率越限的形式,由于电网一般主要传输有功功率,所以分析连锁过载时只考虑有功功率。
3)在计算时,由于缺乏各支路的有功极限Pi(max)的数据,算例中采用虚拟数据进行模拟,并取其为各支路在BPA典型工况下功率的1.8倍。
4)在逐渐增加节点功率时,Δλ的值取为0.03。
此外,为了便于说明,采用支路两端的节点表示形式,如节点16和节点17之间的支路用L16-17表示。IEEE 39节点系统的节点编号可参见图2。
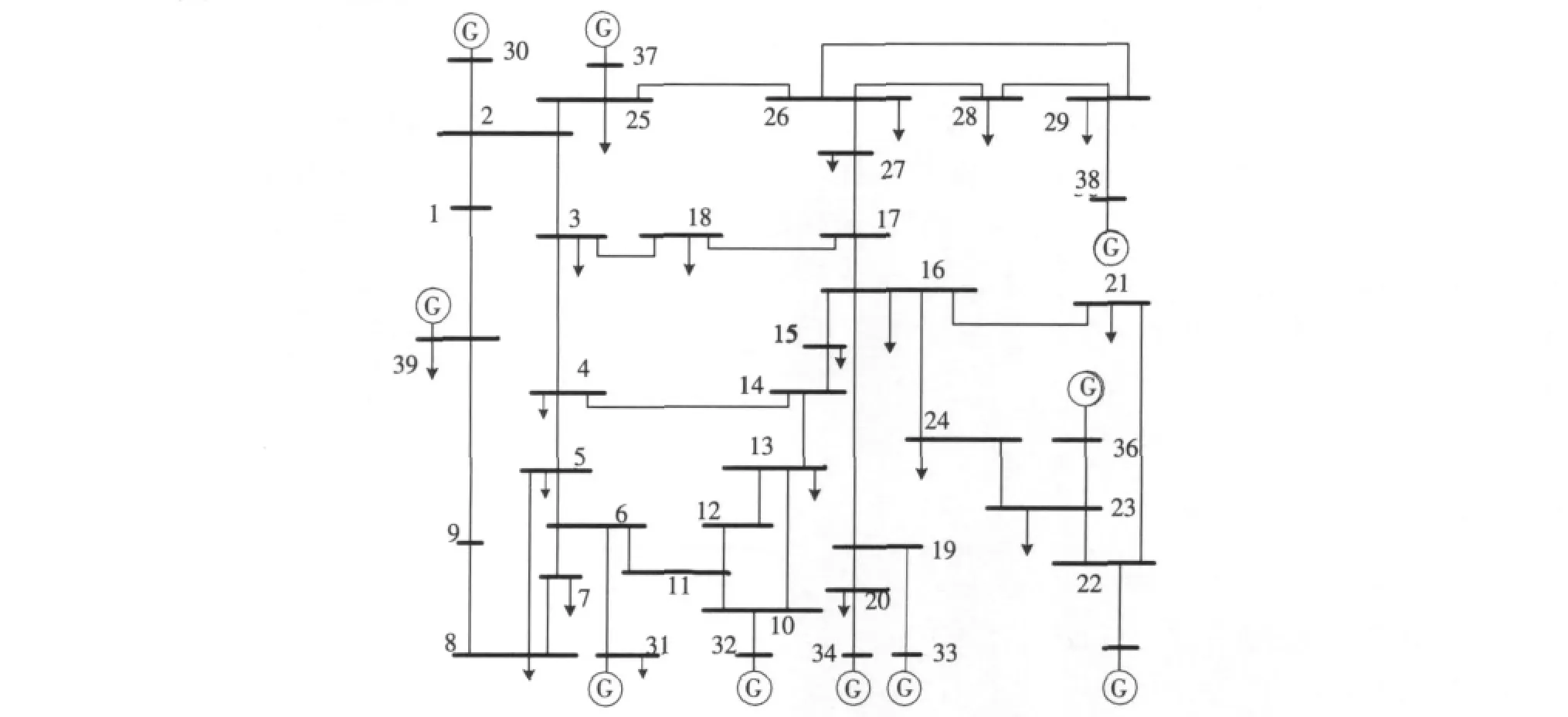
图2 IEEE 39节点系统接线图Fig.2 Diagram of IEEE 39 system
按照前述的算法流程,一共设了6组初始故障支路集,其中前5组(编号分别为G1G2G3G4G5分别列在了表1中。
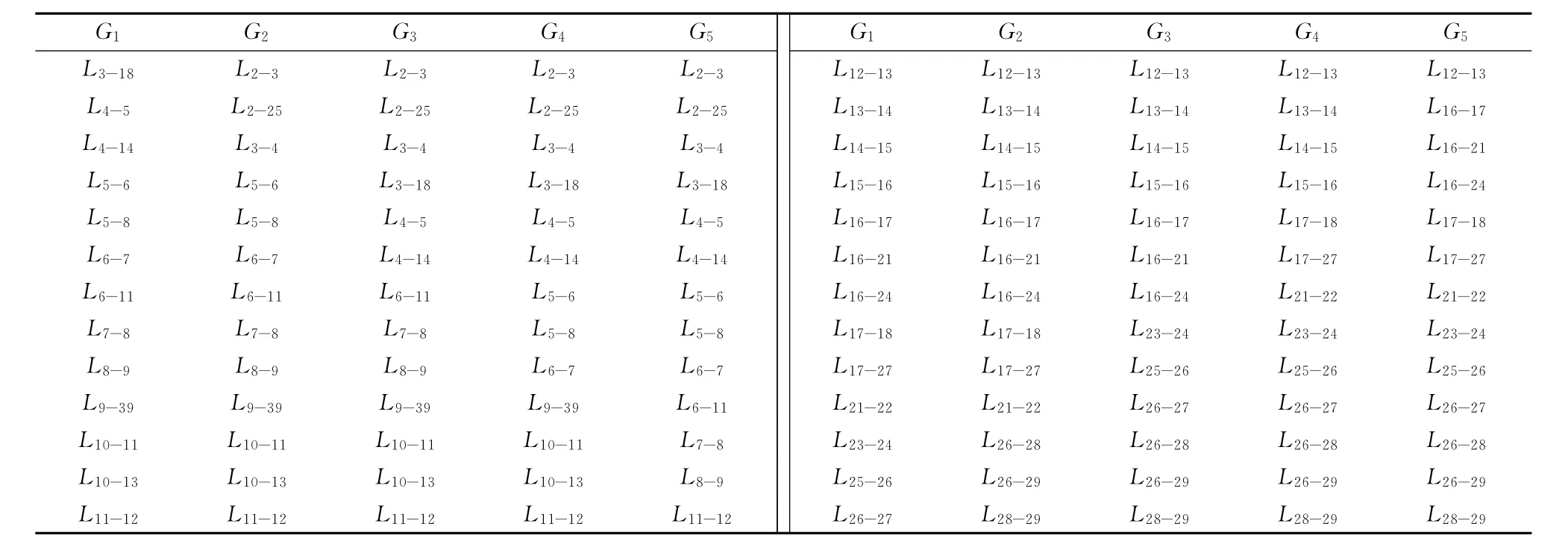
表1 IEEE 39节点系统上的初始故障支路集Tab.1 Sets of initial failure branches in IEEE 39 system
为了能清晰表示,同时又便于比较,这里将分析结果分2次画出。其中,图3画出了G1,G2和G33组的分析结果。图4画出了G4,G5和另外一组(编号为G,其初始故障支路集是前5组的组合)的结果。
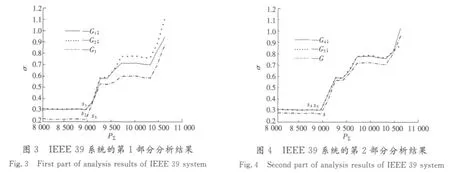
在图3和图4中,横轴为系统的总有功负荷,纵轴为电网在各组初始故障支路集作用下的σ值。由图3和图4可见,此6组分析结果具有相似的表现形式,在此6组初始故障支路集合的作用下,随着系统总负荷水平的提高,σ的值总体呈上升趋势,而且存在着明显的临界点,如图3中的s1,s2和s3以及图4中的s4,s5和s点所示。这说明随着系统总有功负荷的增加,电网的完整性在统计意义下出现了涨落,并呈涨落放大的趋势。
4 进一步的验证
为了进一步验证前述的规律,首先采用IEEE 14节点系统做进一步分析。IEEE 14节点系统见图5。
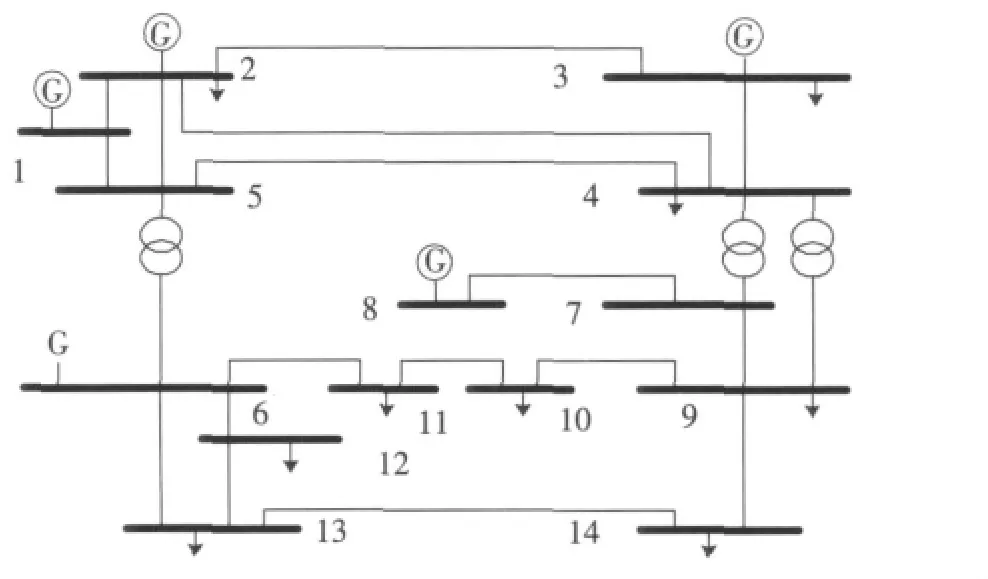
图5 IEEE 14节点系统接线图Fig.5 Diagram of IEEE system
在计算中,初始故障发生前的潮流和支路开断模拟均通过自行编制的程序调用BPA软件来完成,连锁过载的形式也主要考虑功率越限的形式,且只考虑有功功率。在该算例中,各支路有功极限Pimax 的数据取其为BPA典型工况下的功率的2.5倍。在逐渐增加节点功率时,Δλ的值取为0.03。
此外,和IEEE 39节点系统的分析类似,为了便于在后面的表中列写数据,采用支路两端的节点表示形式。IEEE 14节点系统的节点编号可参见图5。
按照前述的流程,此算例一共设置了5组初始故障集合,和IEEE 39节点系统的算例类似,此5组初始故障集合的编号分别为G1,G2,G3,G4,G5,其具体情况可参见表2。
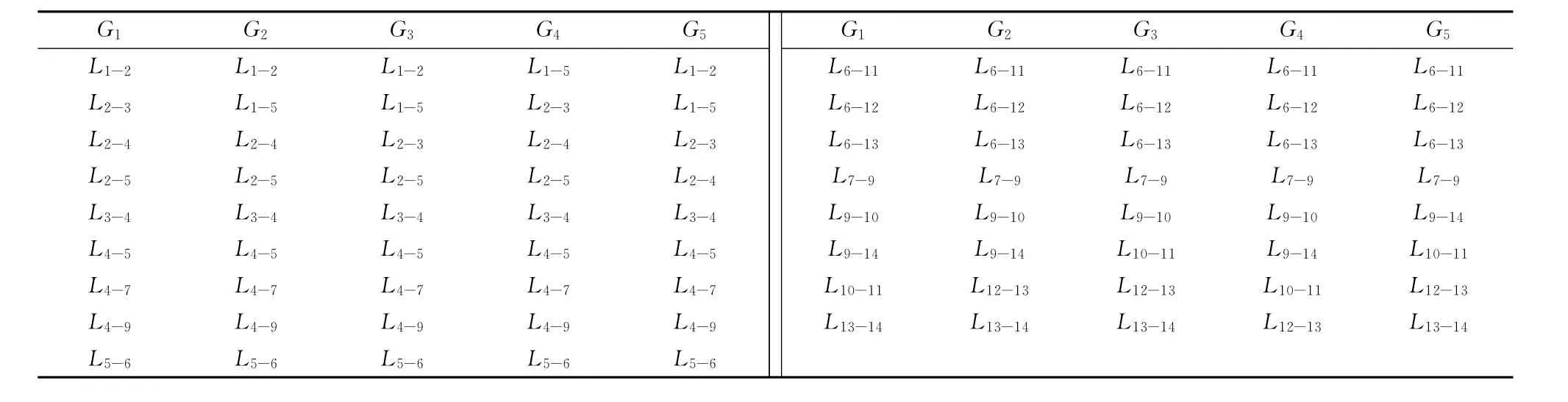
表2 IEEE 14节点系统上的初始故障支路集Tab.2 Sets of initial failure branches in IEEE 14 system
设定初始故障集合之后,按照图1所示的流程分别针对各个初始故障集合进行计算。和IEEE 39节点系统的算例处理办法类似,为了能较为清晰地表示计算结果,这里将G1,G2,G3的计算结果和G4,G5的计算结果分2次画出。
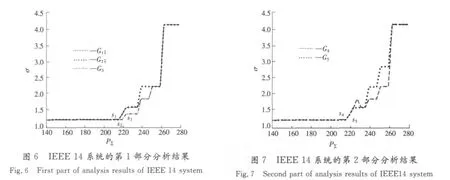
图6给出了G1,G2,G3的计算结果,其坐标轴的含义和IEEE 39系统的算例相同。
由图6可见,在每一组初始故障的作用下,随着系统总负荷水平的提高,σ值总体呈上升趋势,而且存在着明显的临界点,如图6中的s1,s2和s3所示。这和IEEE 39系统上得到的规律是相似的。
图7给出了G4,G52组初始故障支路集合下的计算结果。虽然G5的计算结果在上升阶段有一定的波动,但总体趋势仍然是上升的,和图3、图4以及图6中的结果基本一致。
除了上述算例以外,通过在其他的一些典型系统上进行模拟分析,可以发现,上述图3、图4、图6和图7所示的曲线变化趋势是比较普遍存在的。为了进一步说明,图8给出了IEEE 57节点系统上的一组分析结果。
图8的算例中,各支路有功极限Pi(max)的数据和Δλ的取值与IEEE39节点系统上的算例相同,同时,该算例在分析时将IEEE 57节点系统的80条支路依次作为初始故障支路按照前述的分析流程进行计算,故此不再给出IEEE 57节点系统的接线图。由图8可见,随着电网潮流水平的增加,在同一组初始故障集合的作用下,其统计量σ值的变化趋势和上述图3、图4、图6及图7中是类似的。
总之,通过上述算例可见,在一定的初始故障支路集合的作用下,从统计意义上来说,潮流水平的增加对电网能否保持完整性的影响,存在着临界的情况,当系统的总负荷超过此临界值时,会出现统计涨落放大的现象。按照系统科学的观点 涨落对于系统结构的演化起着重要作用;外部的作用和涨落的放大是促使系统演化的重要原因。
5 结 语
电网连锁过载是在大停电事故中削弱电网结构的常见形式,在深入研究电网连锁过载现象对于电网的安全是比较重要的。本文利用涨落指标,从统计意义上研究了潮流水平对于电网结构的涨落变化的影响,取得一定的规律性认识,可为进一步研究提供一定的借鉴。
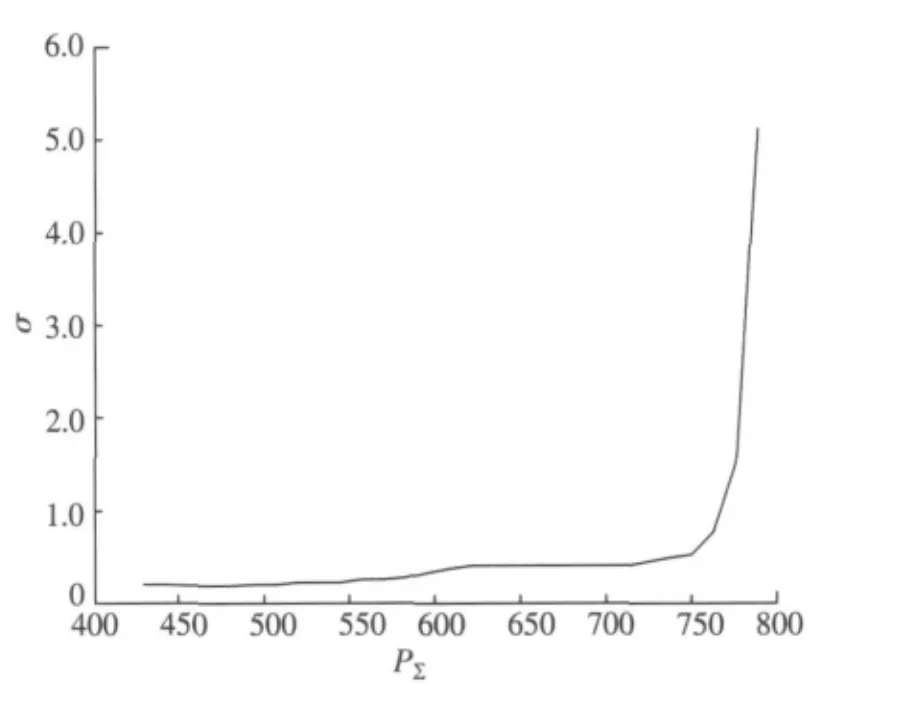
图8 IEEE 57系统的第2部分分析结果Fig.8 Analysis results of an example in IEEE57 system
[1]韩学军,石 磊,朱 岩,等.考虑多重故障的连锁过载分析[J].电网技术(Power System Technology),2008,32(16):86-89.
[2]邓慧琼,李 争,孙丽华,等.电网连锁故障的激发因素研究[J].河北科技大学学报(Journal of Hebei University of Science and Technology),2010,31(3):222-226.
[3]许国志.系统科学[M].上海:上海教育出版社,2000.
Research into fluctuation phenomenon of cascading overload with two stages in power network considering power flow level
DENG Hui-qiong,SU Ai-ning,SUN Ke-jun
(College of Electrical Engineering,Hebei University of Science and Technology,Shijiazhuang Hebei 050018,China)
Aiming at cascading overload phenomenon in power network and considering structural integrity,the fluctuation phenomenon is researched into.Firstly,according to the thoughts that a power network is often weakened by cascading failure of branches,a statistical fluctuation model which can represent the structural integrity of a power network is proposed.Then an example in IEEE 39-bus system with continuously increasing of the injection power of nodes is given.The analysis results show that the fluctuation value of the relative parameter increases with the increase of the total load of the power system,and a critical point exists in that course.At last,in order to further prove that regulation,another example with IEEE 14-bus is analyzed.
power system;cascading failure;cascading overload;power flow level;fluctuation
TM732
A
1008-1542(2012)04-0313-06
2011-12-13;责任编辑:陈书欣
邓慧琼(1972-),男,山西大同人,讲师,博士,主要从事电网连锁故障分析方面的研究。
