从光波的波动方程到薛定谔方程①

米斌周 薛永红 刘 迈

(华北科技学院基础部，北京东燕郊 101601)

从光波的波动方程到薛定谔方程①

米斌周②薛永红 刘 迈

(华北科技学院基础部，北京东燕郊 101601)

通过类比分析光波的波动方程建立了物质波的波动方程，即薛定谔方程。同时引入了量子力学中的三个基本假设，给出了力学量算符的本征方程，对于能量算符，就是定态薛定谔方程。最后初步阐明了量子测量的物理含义。

光波，物质波，薛定谔方程

0 引言

在光的波粒二象性理论中，波动性指光是电磁波，粒子性则指光的量子性，这两种性质通过光子的能量与动量公式联系了起来。如何将粒子性和波动性这两个完全不同的概念统一起来，物理学家们进行了大量艰苦探索。1924年，法国的德布罗意对实物粒子和光进行了对称类比，向前迈出了实质性的一步。他注意到:“确定原子中电子的稳定运动涉及到整数，而至今物理学中涉及整数的只是干涉现象和本征振动现象。这使我想到，不能用简单的微粒来描述电子本身，还应当赋予它们以周期的概念。于是我得出了指导我进行研究的全部概念:对于物质和辐射，尤其是光，需要同时引进微粒概念和波的概念。换句话说，在所有情况下，都必须假设微粒伴随波而存在。”据此，他提出了物质波假设，这一科学假设于1927年被戴维逊(Davisson)和革末(Germer)所做的电子衍射实验所证实。1925年玻恩提出了波粒二象性的概率解释，建立了波动性和粒子性的联系。人们认识到光和一切实物粒子都具有波粒二象性。

可见，在从光波到物质波的认识探索过程中，物理学家们运用了类比的方法。类比是科学认识的重要方法。因此，从光波的波动方程出发，通过类比分析去建立物质波的波动方程是有意义的。

1 薛定谔方程的建立

声波(机械波)由牛顿力学方程确定，光波(电磁波)是由麦克斯韦方程确定的，而实物粒子的物质波需要由1926年奥地利物理学家薛定谔(E.Schrodinger)提出的薛定谔方程确定。描述微观粒子运动状态的波函数ψ满足薛定谔方程是量子力学的一个基本假定。薛定谔方程是基本原理，不能从更基本的原理证明或推导。本文将从光波的波动方程出发，通过物理类比法去建立物质波的波动方程，目的是提供一个比较完整的量子物理图像。这里建立薛定谔方程的过程绝不是这个方程的证明或者推导。

人们在认识物质波之前，已经认识了机械波和光波，机械波和光波都有各自满足的波动方程，我们就从光波说起。众所周知，真空中自由传播的电磁波—光波，也就是光子，所满足的波动方程如下:

(1)式的单色平面波特解为:

光子的概念是爱因斯坦于1905年提出来的。在没有光子概念之前，人们对波函数和波动方程的理解是，波函数ψk描写了单色平面波的性质(例如振幅、频率、波长和传播方向等等)，波动方程(1)全面描述了光波的运动规律。有了光子的概念后，根据爱因斯坦—德布罗意关系式:

由(2)、(3)式易见，波函数同时也描述了光子的力学性质，即能量E和动量p。也就是说光子的这两种性质(波动性和粒子性)通过光子的能量与动量公式联系了起来。光子的相对论力学方程为:

现在，对于波函数ψk，也就是(2)式，有以下运算关系:

力学量用算符表示是经典力学中所没有的一个新概念，也是量子力学中的另一项基本假定。在上述理解的基础上，如果以光子的相对论力学公式(4)作为出发点，只要将各个力学量换成(6)式中相应的算符，并作用于波函数ψ(方程两边消去常数ħ)，就得到了光波的波动方程(1)。只是对于电磁波或光波来说，用这种办法建立波动方程确实没有必要，因为在发现光子的相对论力学关系式(4)之前，已经有了光波的波动方程(1)。物理学中常常运用类比分析的观点解决一些未知的问题，例如德布罗意当年提出物质波的假设，就是运用了对称类比法，当然他的出发点是普朗克辐射定律的推导以及爱因斯坦的狭义相对论。下面我们要做的事情是将这种建立波动方程的办法由光子推广到电子。

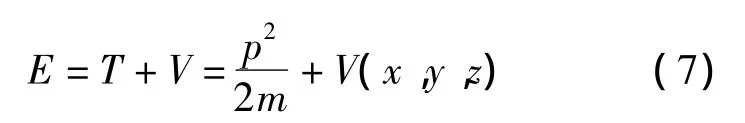
低速电子在保守力场中运动时，基本的力学关系式为:将上式中各个力学量换成相应的算符，并作用于波函数ψ:

这就是物质波的波动方程——薛定谔方程。也就是说，从低速运动粒子的基本力学关系(7)式出发，只要将相应的力学量算符化，并作用于波函数ψ，就很自然地得到了薛定谔方程。

(10)式称为含时薛定谔方程，它在量子力学中的地位相当于经典力学中的牛顿运动方程。至此，运用类比分析的方法建立了物质波的波动方程。同时引出了量子力学中的三个基本假设:

1)微观粒子的运动状态可以用一个波函数ψ来完全描述;

2)描述微观粒子运动状态的波函数ψ满足薛定谔方程;

3)在理论计算中，力学量(实验上可以观测的量)可以用一个算符来表示。

哈密顿量算符(能量算符)的本征方程就是定态薛定谔方程:

在量子力学中，能量E的可能取值由定态薛定谔方程(11)式来决定，ψE(r)则是能量取确定值E的状态的定态波函数。(11)式中的能量算符可以推广到任何力学量A，由力学量算符的本征方程解出的全部本征值，就是相应的力学量A的可能取值。如果用测量仪器测量这个力学量的取值，只能测得其本征值。量子测量会严重干扰被测态。每次测量并且得出结果后，被测状态就会向本次测量所得本征值对应的量子本征态塌缩。而每次测量后系统的状态向哪个本征态塌缩，如同测量会得到哪个本征值一样具有随机性。只有测量后才能知道。这表明微观体系的测量具有不确定性和统计规律。所以量子力学中的测量是对系统状态的破坏。

2 结语

量子力学是现代物理科学中最重要和最成功的理论之一，但其产生的概念和哲学问题及其深奥，犹如一座“迷宫”。就量子理论而言，人们对物理世界仍旧知之甚少。如同爱因斯坦说过的，“量子力学令人印象非常深刻。但是内心的声音告诉我，它还不是真实的东西。这个理论产生了许多东西，但是几乎没有让我们更接近上帝的秘密。无论如何，我坚信上帝不会玩骰子。”

［1］ 钱伯初.量子力学［M］.北京:高等教育出版社，2006

［2］ 张三慧，李椿，滕小瑛，等译.哈里德大学物理学［M］.北京:机械工业出版社，2009

From the light wave equation to the Schrodinger wave equation

MI Binzhou，XUE Yonghong，LIU Mai

(Department of Basic Curriculum，North China Institute of Science and Technology，Yanjiao Beijing-East101601)

Schrodinger’s Equation is established by analogy with the light wave equation，and the three basic hypotheses of quantum mechanics are spontaneously introduced.The eigenvalue equation of mechanical quantity operator is written out，with regard to the energy operator，which is the stationary state Schrodinger equation.Finally，the physical meaning of quantum measurement is initially clarified.

Light wave;Matter wave;Schrodinger’s Equation

0431.2

A

1672-7169(2012)03-0080-02

2012-04-25.基金项目:中央高校基本科研业务费资助(No.JCB1202B)

米斌周(1980-)，男，甘肃庆阳人，硕士，华北科技学院基础部物理教研室讲师。