基于Radon变换和Gabor变换鉴别运动模糊方向角①

加春燕 王 昕

(1.北京工业职业技术学院，北京 100042;2.华北科技学院，北京东燕郊 101601)

基于Radon变换和Gabor变换鉴别运动模糊方向角①

加春燕1②王 昕2

(1.北京工业职业技术学院，北京 100042;2.华北科技学院，北京东燕郊 101601)

对于匀速直线运动的模糊图像，准确鉴别运动方向角是图像复原的关键。分析了运动模糊图像的频谱特征，介绍了Radon变换的数学原理及用其估计运动模糊方向角的思路、步骤和数值实验结果。由于实际拍摄的模糊图像在很多时候频谱特征不够明显，导致用Radon变换鉴别角度出现大的误差，为此，提出了基于Gabor变换的一种改进算法。算法运用“窗口”聚焦频谱图像中心，较好地消除了噪声干扰并克服了Radon变换的弊端，数值实验结果验证了该算法的有效性。

运动模糊方向角鉴别;运动模糊频谱特征;Radon变换;Gabor变换

0 引言

实际成像过程中，因相机与被摄物体之间存在相对运动而造成的运动模糊是一种常见的图像降质现象。在所有运动模糊中，由匀速直线运动造成的模糊图像更具有一般性，这是因为变速、非直线运动在一定条件下可被视为或分解为分段匀速直线运动。匀速直线运动模糊效应主要由两个参数决定:一是运动方向角，二是运动尺度。文献［1-4］中已指出，只要估计出运动方向，则可将二维图像沿该方向降解为一维数据，从中能够较容易地估计出运动尺度。因此，准确鉴别运动模糊方向尤为重要。

现有的运动模糊方向的鉴别方法主要包括:陈前荣等［1］采用3×3方向微分乘子结合双线性插值来鉴别运动方向，鉴别精度较高，但计算量太大不够实用;谢伟等［2］采用求模糊图像倒频谱及分析谱上特征点的方法估计运动方向，该方法简单易行，但对于实际生活中千差万别的图像，大多图像倒频谱上的特征点不够明显，此时该方法失效;Lokhande等［3］根据模糊频谱特性，利用Hough变换来鉴别运动方向，但如果模糊特征不是很明显，利用该方法鉴别运动方向会很困难;M.Ebrahimi Moghaddam 和 M.Jamzad［4］采用 Radon变换估计θ，取得了不错的效果，是目前运用最为广泛的方法，但在图像会受噪声干扰的情况下估计有误差。本文基于运动模糊图像的频谱特征，提出一种基于Gabor变换的改进方法，力图更加准确有效地鉴别运动模糊方向角。

1 匀速直线运动模糊模型简介

对于匀速直线运动模糊，图像的退化过程可近似抽象为以下模型［5］:

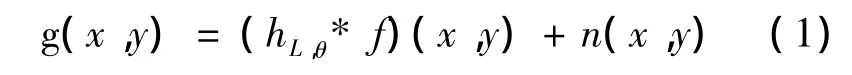
其中，g为运动模糊图像，hL，θ代表运动模糊的点扩散函数(PSF)，f是未降质的清晰图像，n为加性噪声函数，*表示卷积运算。

运动模糊的点扩散函数 kL，θ的一般表达式为［6］:

可见，确定hL，θ的关键在于两个重要参数:一是运动方向角θ，二是运动尺度L，准确鉴别θ和L是运动模糊图像复原的前提和关键。由于L的估计又要依赖于运动方向θ，因此，运动方向θ的准确鉴别具有重要意义。

由卷积原理，对模型方程(1)做 Fourier变换，得到频域上的方程:

其中H(u，v)是一个sinc函数，因此，如果运动模糊图像受噪声污染较小，则相应的Fourier频谱图像中会出现平行的暗条纹，且暗条纹方向与运动方向垂直［3-7］。图1展示了运动模糊图像(L=10，θ=45°)及其频谱图像，从频谱图像中可以清楚看到与运动方向垂直的暗条纹特征，H(u，v)中的平行暗线与sinc函数特征是基于图像频谱信息来估计运动方向θ的最重要依据。

图1 运动模糊图像及其Fourier频谱图像

2 基于Radon变换的运动模糊方向估计

2.1 Radon变换原理

对于函数 G(u，v)，其 Radon 变换为［4］:

图2展示了Radon变换的定义，对于直线l上任意一点 (u，v)，由图 2可知，u= ρcosθtsinθ，v= ρsinθ+tcosθ，t∈(-∞，+∞)，因此，G(u，v)的 Radon变换是沿着距原点(图像中心)ρ且与竖轴夹角为θ的直线的积分。

图2 Radon变换定义示意图

事实上，Radon变换可以理解为图像在ρθ平面上的投影，ρθ平面上的每一点都对应着uv平面上的一条线。由于Radon变换是图像像素点在每一条直线上的积分，因此，图像中一条高灰度值的线就会在ρθ平面上形成一个亮点，低灰度值的线则会形成一个暗点，所以图像平面中直线的检测就转化为在参数平面中对亮、暗点的检测［7］。

2.2 Radon变换鉴别运动模糊方向角

针对一幅图像，当θ一定，ρ取遍图像范围内所有值时，累计得到θ方向所有直线的积分值，令θ从0°～180°变动，则得到所有方向的Radon变换值，由运动模糊频谱图像的平行黑线特征可知，Radon变换的最大值对应的角度即为鉴别出的运动方向角。需要注意的是，Radon变换要计算函数沿各个方向直线的积分，而对于有限的图像(一般是矩形)来说，对角线上的线段最长，积分结果会比较大，因此用Radon变换常常错误的估计出45°或者135°，为了克服这种现象，可以对图像预先归一化，即逐点除以和图像大小相同的全1矩阵，再进行Radon变换。

综上，用Radon变换鉴别运动方向角的一般步骤为:

1)通过二维傅里叶变换，求运动模糊图像g(x，y)的频谱2)归一化

3)对|G(u，v)|取对数，以压缩谱动态范围，使频谱特征更明显;

4)做0°～180°的Radon变换;

5)找出变换后的最大值，此最大值所对应的角度即为鉴别出的运动方向。

图3展示了对图1中的频谱图像做Radon变换的结果，真实的角度是45°，Radon变换的结果对应图3中最亮的地方，角度为45.012°，可见鉴别结果很准确。

图3 Randon变换估计运动方向

2.3 Radon变换存在的问题

实际运动模糊图像千差万别，且易受到噪声干扰，从而导致频谱特征并非都像图1那样明显，当频谱中的暗条纹不够平行和整齐时，用Radon变换来检测角度会出现很大的误差。图4展示了2个频谱图像a和b，真实方向分别是5°和85°，但用Radon变换检测出的角度分别是0°和45°，误差非常大。注意到频谱图像中心存在很亮的白色条带，一个很自然的想法是，能否利用这一特征来估计角度?这需要聚焦图像的局部区域，Gabor变换便可以很好地解决这一问题。

图4 两个运动模糊频谱图像，真实角度分别为5°和85°

3 基于Gabor变换和Radon变换鉴别运动模糊方向角

3.1 理论分析

经典的Fourier变换只能反映信号的整体特性(时域，频域)，不能给出在各个局部时间范围内的谱信息描述，然而在实际应用中很多时候更关心的信号局部范围内的特性，为此，D.Gabor于1946年提出了一种新的变换方法—Gabor变换。设f∈ L2(R)，则 Gabor变换定义为［9］)

事实上，Gabor变换是一种加窗的Fourier变换方法，就是用一个窗函数g(t-b)与信号f(t)相乘实现在b附近开窗和平移，然后进行Fourier变换。针对二维图像，算法中选取Gaussaion函数作为窗函数，定义如下:

3.2 算法实施步骤

由于频谱图像在中心部位的平行条带结构受角度和噪声的影响较小，因此把窗口开在图像中心附近。在数值实验中，取a=625，则窗口宽度为50像素。综上，基于 Gabor变换和Radon变换鉴别运动模糊方向的具体步骤如下:

1)令 b=(mcosα，msinα)，α∈［0，2π］，m∈［-20，20］，则可得到图像中心各个方向小窗口的Gabor频谱图像;

2)对每个Gabor频谱图像做Radon变换检测角度;

3)取所有检测结果的均值作为运动方向角的估计值。

3.3 仿真结果与误差分析

图5是用Gabor变换和Radon变换对图4检测角度的结果，Gabor变换将窗口聚焦在图像中心区域，通过Radon变换检测出的直线标记在图5中，检测结果分别为4.967°和86.026°，与真实角度5°和85°非常接近。高斯函数的Fourier变换仍为高斯函数，这使得Fourier逆变换也是用窗函数局部化，体现了频域的局部化;二是“测不准原理”表明，时间和频率函数的窗口宽高乘积有一个最小值，而这个最小值对应的Gabor变换的最优窗函数恰好为Gaussian函数，且窗口宽为

图5 基于Radon变换和Gabor变换鉴别运动模糊方向角

为了进一步验证算法的准确度，选择matlab自带图像Lena 512×512进行数值实验，实验中先用“fspecial”命令人为设置运动模糊，运动方向从水平正向开始每隔30°取一个值，运动尺度分别为10像素、20像素和40像素，实验结果如表1所示。

表1 Lena 512×512实验结果

从实验结果来看，只用Radon变换估计角度时，部分方向(如60°)的误差绝对值高达15°，而用本文的Gabor变换+Radon变换鉴别角度，对测试的所有方向，小尺度(10像素)时误差绝对值不超过3°，大尺度(40像素)时误差绝对值均为0°，可见用本文的改进算法鉴别运动模糊方向更加有效。此外，小尺度运动模糊时，鉴别误差相对较大，这是因为小尺度对应的频谱图像中暗条纹数目较少，中心主瓣变得很宽，导致鉴别误差较大。

4 结语

运动模糊参数估计是运动模糊图像复原的重要步骤，文中主要研究了运动方向角的估计方法。通过分析运动模糊图像的频谱特征，即平行暗条纹和sinc函数结构，为鉴别运动角度找到突破口。介绍了Radon变换的数学原理及用其鉴别运动方向角的思路和步骤，在数值实验中发现问题，进而提出了基于Gabor变换的改进方法。通过数学原理分析和大量数值实验，验证了该方法的有效性，为后续进行运动模糊图像复原奠定了基础。

［1］ 陈前荣，陆启生，成礼智.基于方向微分的运动模糊方向鉴别［J］.中国图象图形学报，2005，10(5):590-595

［2］ Xie Wei，Qin Qianqing.Estimating blur parameters of point spread function of motion-blurred image based on cepstrum［J］.Geomatics and Information Science of Wuhan University，2008，33(2):128-131.(in Chinese)

［3］ Lok Hande R，Arya K V.Identification of parameters and restoration of motion blurred images［J］.Chinese Journal of Computers，2007，30(4):686-692

［4］ Moghaddam M E，Jamzad M.Finding point spread function of motion blur using Radon transform and modeling the motion length［C］//IEEE 4th International Symposium on Signal Processing and Information Technology(ISSPIT)，2004:14-17

［5］ 孙兆林.Matlab 6.x图像处理［M］.北京:清华大学出版社，2002

［6］ Chan T F，Shen J.Image processing and analysis［M］.Philadelphia:SIAM，2005

［7］ 苏军.基于频谱分析的运动模糊图像的参数鉴别［J］. 电子科技，2011，24(7):77-79

［8］ 王敏，田启川.改进的运动模糊图像复原算法［J］. 图形图像与多媒体，2011，30(6):37-40

［9］ 崔锦泰.小波分析导论［M］.西安:西安交通大学出版社，1995

［10］ 贾朱植，董立文.Fourier变换和Gabor变换与小波变换的研究［J］.鞍山科技大学学报，2005，28(1):12-16

Identification of Motion Direction from Motion Blurred Images Based on Radon Transform and Gabor Transform

JIA Chunyan1，WANG Xin2

(1.BeijingPolytechnic College，Beijing 100042;2.North China Institute of Science and Technology，Yanjiao Beijing-East 101601)

In order to recover the uniform linear motion blurred image，it’s necessary to identify the motion direction.Based on the spectrum characteristics of motion blurred image，the mathematic principle of Radon transform and procedures of using it to identify the motion direction were introduced.Aiming at the spectrum characteristics of the real blurred images taken by digital camera is not obvious，an improved algorithm based on Gabor transform is proposed.The algorithm uses a"window"focusing on the spectrum center of the image to eliminate noise interference and overcome the drawbacks of Radon transform.Numerical experimental results show effectiveness of the presented method.

identification of motion angle;motion blur spectrum characteristics;Radon transform;Gabor transform

TP391.4

A

1672-7169(2012)03-0019-04

2012-04-27

加春燕(1983-)，女，山西临汾人，硕士，北京工业职业技术学院讲师，研究方向:数学教学和数学应用研究。