基于SPOT5影像的杉木胸高断面积估测探讨
2012-12-26陈柏海
陈柏海,林 辉,孙 华
(中南林业科技大学林业遥感信息工程研究中心,长沙410004)
基于SPOT5影像的杉木胸高断面积估测探讨
陈柏海,林 辉,孙 华
(中南林业科技大学林业遥感信息工程研究中心,长沙410004)
采用角规实地调查黄丰桥林场90个杉木人工纯林样地胸高断面积,利用样地SPOT5遥感信息与地理信息,建立了杉木胸高断面积多元线性回归估测模型。首先对样地采用GIS软件进行缓冲处理,缓冲后每个样地的面积为1 hm2;然后提取样地遥感光谱信息与纹理信息等21个因子和4个GIS因子,采用逐步回归分析法筛选出6个因子作为模型自变量;最后分别采用普通最小二乘法(OLS)和偏最小二乘法(PLS)建立了杉木胸高断面积多元回归模型。研究结果表明:OLS回归模型的预测精度为82.2%,均方根误差(RMSE)为5.12 m2/hm2;PLS回规模型的预测精度为83.9%,均方根误差(RMSE)为4.21 m2/hm2,PLS和OLS回归模型在杉木胸高断面积估测中均取得了较好的效果,用中高分辨率遥感影像在估测森林结构参数上是可行的。
胸高断面积;多光谱;SPOT5;多元统计分析
近年来,随着高空间分辨率遥感影像的广泛应用,GIS和GPS技术在森林资源调查和管理中应用的普及,在给外业工作者带来极大方便的同时,也为借助3S技术对森林结构参数进行定量估测提供了所需的必要条件[1]。国外学者对此做了大量的研究[2-6]。研究表明,利用中高分辨率遥感影像各波段的灰度值线性或非线性的组合,能较好地反映森林的生长状况和分布关系,与蓄积量、结构参数都有很好的相关关系,可作为定量因子,建立杉木胸高断面积估测模型。
采用SPOT5影像作为遥感数据源,以研究区域1∶1万地形图经矢量化生成的DEM图作为GIS数据源,对影像数据进行预处理,并提取相应的RS和GIS因子,结合地面实测数据,利用SPSS统计分析软件,用普通线性回归分析方法和偏最小二乘法,建立研究区的杉木胸高断面积估测模型,为快速、高效、准确地估测杉木胸高断面积提供理论依据。
1 材料与方法
1.1 数据获取与处理
1.1.1 研究区概况
研究区位于株洲攸县黄丰桥国有林场内,总面积351.16 km2。林区内森林多样性比较丰富,有木本植物400余种,主要以杉木、马尾松人工林为主,各龄组分布合理。
1.1.2 SPOT5 数据
研究采用的数据拍摄时间为2009年11月28日3时6分13秒,它包含空间分辨率为10 m的4个多光谱波段,即绿波段(500~590 nm)、红波段 (610~680 nm)、近红外波段(780~890 nm)与短波红外波段(1 580 ~1 750 nm)和分辨率为 2.5 m 的全色波段[7]。影像的拍摄太阳高度角和方位角分别为45.11°和158.74°。利用ENVI软件对SPOT5影像进行预处理,主要包括辐射定标、大气校正、几何校正等。
1.1.3 外业调查与内业整理
外业调查时间为2009年10月至2010年11月,采用角规抽样的方法对林分进行调查。在研究区范围内,首先对影像进行初步解译和判读,对杉木人工纯林所在的位置和面积进行分析和计算,以确定样地布设的位置和数量要求。外业调查主要针对杉木中龄林和近熟林,并用带坡度改正的角规调查林分每公顷断面积,用激光测距仪或皮尺测量水平距离来确定边界木;用GPS定位样地坐标。在本次外业调查和相应的数据处理过程中都采用WGS-84坐标系统,以保证样地的位置准确。
外业调查资料录入计算机统计整理,形成与样地相对应的每公顷杉木断面积;然后样点在SPOT5影像上缓冲面积为1 hm2的样圆,以减少因GPS定位所带来的误差。由此,建立了地面调查点对应像元、像元灰度值和胸高断面积之间的一一对应关系,为杉木胸高断面积估测模型的建立提供依据。
1.2 变量设置
利用SPOT 5遥感影像,选取一系列可能与断面积估测相关的RS因子及DEM图中提取的GIS因子,作为断面积估测的自变量因子,以地面实测样点断面积为因变量,建立多元回归模型。原始波段信息有多光谱波 B1,B2,B3,B4(也就是 SWIR,短波红外波段)和全色波段PAN及相应波段的标准差;波段比值有可见光的 B1/B2(GRENRED),B4/(B1+B2)(SVR),B4/B3(MSI),(B3 - B2)/(B3+B2)(NDVI),B3/B2(RVI);纹理信息主要是能量(ASM)、对比度(CON)、相关(COR)、熵(ENT)、逆差距(IDM)、方差(VAR);在GIS因子方面,设置的主要因子有海拔、坡度、坡向、阴影等。共设置25个自变量。
1.3 解算方法
1.3.1 逐步回归分析
多元逐步回归法的基本思路在于,自动地从大量可供选择变量中选取最重要的变量,根据自变量对因变量作用程度的大小,保留作用程度大的变量,剔除作用小的变量[8],变量的引入和剔除是同时进行的。循环反复计算,直到所有该引入的变量都被引入,该剔除的变量均被剔除为止,保留的变量组合即为最优变量组合。
1.3.2 偏最小二乘法
偏最小二乘法是在建模过程中,集主成分分析、典型相关分析和线性回归分析的特点,实现回归建模、数据结构简化以及变量之间的相关性分析。因此,它在分析结果中,可以提供一个更为合理的回归模型[9]。一般情况下,偏最小二乘法回归分析法并不需要选取所有m个成分来建立回归方程,只需选用前h个成分,即可得到满意的回归模型。同时对结果进行交叉有效性检验(Q2),当Q2h≥0.097 5时,可认为引进新成分th会对模型预测能力有明显改善作用。
1.3.3 精度评价方法
确定系数(R2)、均方根差(RMSE)、相对误差(RE)是常用的对模型预测值和实测值之间进行评价和验证的方法,其定义如下[8]:
确定系数(R2)可以用来检验估计值与实测值之间的线性显著程度,变化范围在0≤R2≤1,其中R2越接近于1,表明模型的预测能力越强,模型效果显著。
均方根误差(RMSE)表示实测值与估计值之间的离散程度,其值越小表示模型估计值与实测值之间的相对距离比较接近,即模型预测精度就越高。
相对误差(RE)评价是以相对误差绝对值的平均值作为模型精度评价指标,其值越小,模型的预测精度就越高。
计算公式:

式中:yi为实测值,为模型估计值,为实测平均值,n为样本数。
2 结果与分析
2.1 自变量分析与筛选
自变量的选择是建立回归模型的关键。在建立的回归模型中,应尽可能的剔除那些对断面积估测没有重要解释作用的变量,从而达到简而精的要求。
从总体90个样本中,按断面积大小分段选取70个样本作为建模数据,其中包括最小断面积与最大断面积样本数据;剩余20个样本作为检验数据。计算各因子与断面积之间的相关系数及方差扩大因子(VIF),结果见表1。
分析表1可知:与断面积相关系数较大前3个变量是MSI、SVR、能量,说明这3个变量与断面积有较好的相关性;负相关性方面居前3个变量是GRENRED、坡向、对比度,且这3个变量的绝对值都大于0.1。在所设置的25个自变量中,方差扩大因子(VIF)大于10的有10个,表明它们之间存在多重相关性,若将这些因子全部纳入方程,估测模型的精度将无法保证。
在模型的筛选过程中,采用逐步回归分析方法,以回归系数显著性检验中各自变量的F统计量的临界概率值FSig≤0.05和 FSig≥0.10作为自变量引入或剔出模型的判断标准,即:当Fin≥F0.05,该变量被引入模型,否则不引入;如果 Fout≤F0.10,该变量被剔除,否则保留。共选取了6个自变量:MSI,能量,B3MEAN,B4S,熵,GRENRED。
2.2 最小二乘法分析
2.2.1 基于最小二乘法回归模型的建立
利用逐步回归分析所筛选出的6个自变量,相应的断面积为因变量,用最小二乘法建立多元线性回归模型。模型统计量见表2。

表1 遥感和GIS因子及其相关信息

表2 模型统计量
在表2中,复相关系数R=0.736,确定系数R2=0.542,校正确定系数 R2adj=0.496,估计值标准误 =5.091。
方差分析结果见表3。
在表3中,可知模型回归平方和为1 958.51,剩余平方和为1 634.30,总平方和为3 592.80,检验回归方程的统计量 F值 =12.58,查 F检验表可得临界值F0.05(6,63)=2.25,F > F0.05(6,63)表明模型在显著性水平α=0.05下通过回归方程检验,即所建回归模型有效。也可通过表中显著性值=0.0009<0.05来直接判断回归方程通过F检验(这里显著性表示弃真概率,含义下同)。

表3 方差分析
回归系数表见表4。
在表4中,各自变量的回归系数:B4S=-3.176,B3MEAN=1.621,GRENRED= -0.2541,MSI=19.25,熵=9.214,能量=32.90;同时可知各变量所对应的t值及显著性值,在表中各自变量显著性值均小于0.05,表明在显著性水平α=0.05下模型自变量各个回归系数通过t检验,具有显著性。
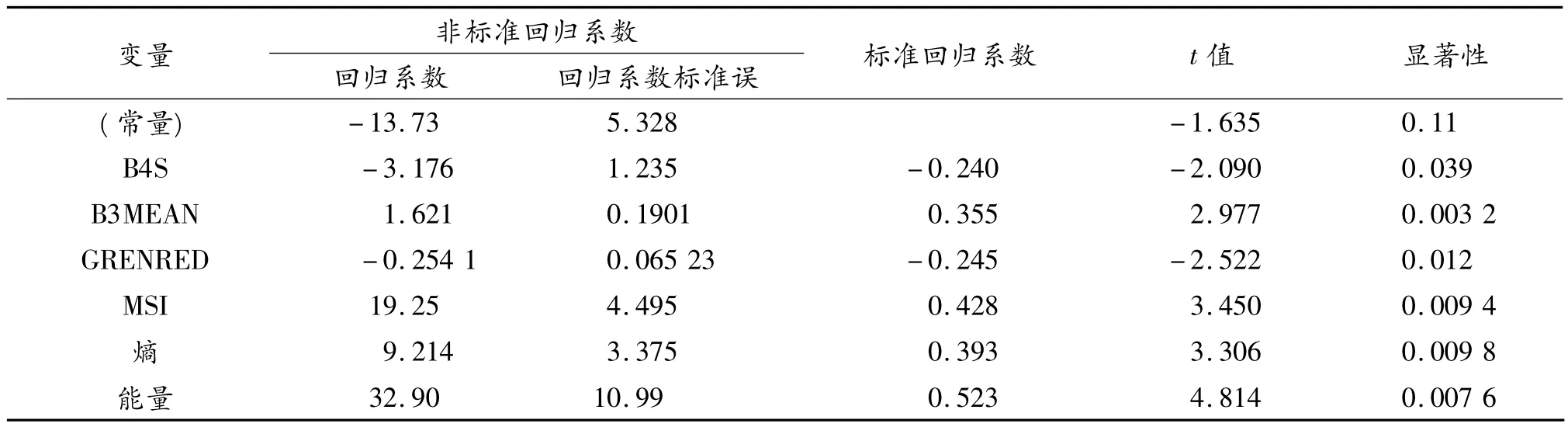
表4 模型回归系数
综上所述,用筛选所得的6个自变量建立的拟合回归方程为:
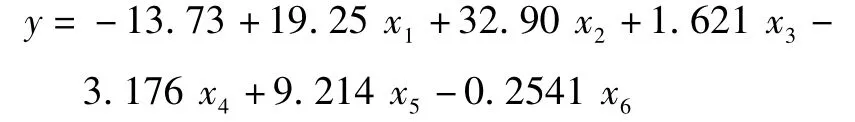
式中:x1表示 MSI,x2表示能量,x3表示 B3MEAN,x4表示B4S,x5表示熵,x6表示GRENRED。
2.2.2 模型精度检验
利用20组检验数据对建立的断面积估测模型进行预测精度检验,检验结果见表5。

表5 模型精度检验结果
以20组检验数据的预测值为横坐标,实测值为纵坐标,绘制散点图,如图1所示。
由表5和图1可知:以多光谱波段的绿红波段比值、水分胁迫指数、纹理信息中的能量、熵、全色波段的标准差为自变量,用最小二乘法建立的杉木胸高断面积估测模型,它的确定系数值为0.673 1,均方根误差值为 5.12 m2/hm2,预测精度达到 82.2% 。

图1 断面积估计值与实测值比较
2.3 偏最小二乘法分析
2.3.1 基于偏最小二乘法回归模型的建立
利用逐步回归分析所筛选出的6个自变量,相应的断面积为因变量,用偏最小二乘法建立多元线性回归模型。
偏最小二乘法的前5个成分的统计信息见表6。
由表6可知:校正确定系数R2adj随着成分的增加而增大,当成分个数为3时,校正确定系数R2adj达到最大,其值为0.515,同时交叉检验因子Q23=0.101 >0.097 5,表明只需提取自变量的前3个成分就可用建立精度较高的回归模型。
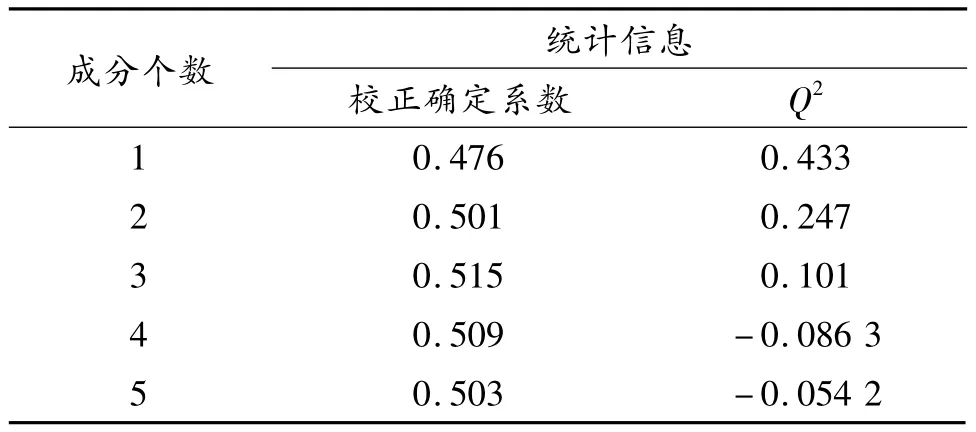
表6 偏最小二乘法统计信息
因此,设定自变量提取成分数为3,其回归系数和变量投影重要性指标见表7。

表7 回归系数与变量投影重要性表
变量投影重要性指每一个自变量对因变量集合的解释能力,可通过变量投影重要指标值来测度。由表7可知:在所提取的3个成分中,按变量投影重要性指标值大小排序,可得6个自变量在估测模型中重要程度次序为:MSI>ASM>GRENRED>ENT>B3MEAN>B4S。同时,由此可得回归模型为:

式中:x1表示 MSI,x2表示能量,x3表示 B3MEAN,x4表示B4S,x5表示熵,x6表示GRENRED。
2.3.2 模型精度检验
利用20组检验数据对建立的断面积估测模型的预测精度进行检验,检验结果见表8。

表8 模型精度检验结果表
以20组检验数据的预测值为横坐标,实测值为纵坐标,绘制散点图如图2所示。

图2 断面积估计值与实测值比较
由表8和图2可知:以多光谱波段的绿红波段比值、水分胁迫指数、纹理信息中的能量、熵、全色波段的标准差为自变量,用偏最小二乘法建立的杉木胸高断面积估测多元线性回归模型,其确定系数0.698 9、均方根误差值为4.21 m2/hm2、预测精度达到83.9%。
3 结论与讨论
本研究是在较小范围内利用中高分辨率遥感影像对杉木胸高断面积进行估测分析,主要是探索利用中高分辨率在森林结构参数建模中的应用能力。
1)利用SPOT5影像灰度值线性与非线性组合等25个自变量因子,经过逐步回归筛选出6个自变量,同时按断面积大小分段选取70个样本作为建模数据,其中最小断面积与最大断面积必取,建立多元线性回归模型;将剩余的20个样本数据代入估测模型进行精度评价。其中最小二乘法估测精度为82.2%、偏最小二乘法为估测精度为83.9%,达到了较为理想的预测效果。
2)在建立回归模型时,通过两种不同的解算方法——最小二乘法(OLS)与偏最小二乘法(PLS),分别建立了两种杉木胸高断面积估测模型。比较可知,用PLS解算方法建立的估测模型比OLS建立的估测模型在估测精度上提高1.7%,每公顷断面积估测的均方根误差提高约1 m2/hm2,说明用PLS建立的回归模型更能接近实测值。
总体来说,用中高分辨率的遥感影像来估测杉木胸高断面积是可行的。同时,研究也存在着一定的不足:首先,因研究区域范围不大,实测的总体样本数据比较少,具有很强的地域性;其次,本研究对杉木胸高断面积估测模型的自变量的筛选,仅使用逐步回归分析来筛选自变量,没有考虑其它可能存在对估测模型影响较大的自变量因子。
[1]李崇贵,赵宪文,李春干,等.森林蓄积量遥感估测理论与实现[M].北京:科学出版社,2006.43 -48.
[2]W Roberts,S Tesfamichael,M Gebreslasie,et al.Forest structural assessment using remote sensing technologies:an overview of the current state of the art[J].Southern Hemisphere Forestry Journal,2007,69(3):183-203.
[3] Ingram JC,Dawson TP and Whittaker RJ.Mapping tropical forest structure in south-eastern Madagascar using remote sensing and artificial neural networks[J].Remote Sensing of Environment,2005(94):491-507.
[4]Maselli F,Chirici G,Bottai L,et al.Estimation of Mediterranean forest attributes by the application of k-NN procedures to multitemporal Landsat ETM+images[J].International Journal of Remote Sensing,2005,26(17):3781 -3796.
[5]Wolter P,P.Townsend,and B.Sturtevant.Estimation of forest structural parameters using 5 and 10 meter SPOT - 5 satellite data[J].Remote Sensing of Environment,2009,113:2019 -2036.
[6]Song,C.Estimating tree crown size with spatial information of high resolution optical remotely sensed imagery[J].International Journal of Remote Sensing,2007,28(15):3305 -3322.
[7]林辉,孙华,熊育久,等.林业遥感[M].北京:中国林业出版社,2011.64 -69.
[8]袁志发,周静芋.多元统计分析[M].北京:科学出版社,2006.138-145.
[9]王惠文.偏最小二乘回归方法及其应用[M].北京:国防工业出版社,1999:200 -220.
Study on Basal Area Estimation of Chinese Fir Based on SPOT5 Images
CHEN Baihai,LIN Hui,SUN Hua
(Research Center of Forestry Remote Sensing& Information Engineering,Central South University of Forestry& Technology,Changsha 410004,Hunan,China)
Abstyact:The surveying of Chinese fir basal area by fielding 90 sample plots with angle gauges had been carried out in Huangfengqiao forest farm,the multiple linear regression estimation model of basal area was set up based on remote sensing and geographic information.First,each sample plot was buffered by GIS software to 1 hectare;Then from which 21 RS index factors such as spectral and texture information and 4 GIS index factors were extracted,in which 6 index factors were screened out as independent model variables through stepwise regression analysis;Last the multiple regression model was built by using OLS and PLS respectively.The results showed that:the model predicted accuracy was 82.2%and RMSE was 5.12 m2/hm2by using OLS;the model predicted accuracy was 83.9%and RMSE was 4.21 m2/hm2by using PLS;The adoption of OLS and PLS services well in basal area estimation,to estimate forest structural parameters can achieve good effects by using high resolution remote sensing images.
basal area;multispectral;SPOT5;multivariate statistical analysis
TP 79;S 757.2
A
1003—6075(2012)01—0044—05
2011—11—21
2011—12—13
湖南省高等学校科学研究项目“高分辨率遥感影像森林结构参数反演研究”(11C1313)。
陈柏海(1987—),男,湖南双牌人,硕士,主要研究方向为遥感与林业信息工程。
