为非厄米情况下的薛定谔方程及其应用
2012-12-25马晓春赵先林刘金海
马晓春,赵先林,刘金海
(1.郑州轻工业学院技术物理系,河南郑州450002;2.河南教育学院物理系,河南郑州 450046)
马晓春1,赵先林2,刘金海2
(1.郑州轻工业学院技术物理系,河南郑州450002;2.河南教育学院物理系,河南郑州 450046)
给出了为非厄米情况下的薛定谔方程,并对其性质、意义及应用进行了讨论.
辐射阻尼;非厄米的;薛定谔方程
0 引言
薛定谔方程是量子力学的一个基本假设,是无法推导和证明的,然而,它可以通过经典的波动方程和德布罗意关系得到[3].根据这一做法,也可以得到为非厄米算符时的薛定谔方程.在阻尼力F=-γ的作用下的波动方程为


2.1 本征值的意义

从以上不难看出,复能量的实部就是通常意义下的能量,其虚部表示该能级的自然宽Γ.
2.2 本征波征函数性质
(1)从(11)式可知,此时系统的定态波函数随时间指数衰减,概率密度也随时间指数衰减.
(2)概率流密度随时间指数衰减,连续性方程需要修改.

3.1 一维线形谐振子

3.2 色散的量子理论
按照洛伦兹的经典理论,原子可以看做谐振子.光作用在原子中的电子上时,相当于引入围绕算符

利用和文献[3]类似的方法,只需作如下替换

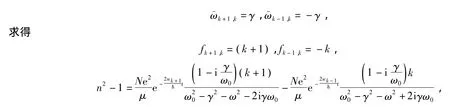
其中第一项表示辐射,第二项表示受激吸收.
该结果表明:考虑到辐射阻尼后,折射率为复数.这一结论已被大量实验所证实.该结果还表明:折射率随时间指数衰减.这一结论有待实验验证.
4 结论
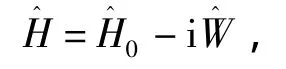
[1]王正行.量子力学原理[M].北京:北京大学出版社,2003:138-144.
[2]李正道.场论与粒子物理学:上册[M].北京:科学出版社,1982:207.
[3]索科洛夫A A.量子力学原理及其应用[M].王祖望,译.上海:上海科学技术出版社,1983:304-309.
Schrödinger Equation and Its Application foras Non-Hermitian
MA Xiao-chun1,ZHAO Xian-lin2,LIU Jin-hai2
(1.Department of Technology and Physics,Zhengzhou University of Light Industry,Zhengzhou 450002,China; 2.Department of Physics,Henan Institute of Education,Zhengzhou 450046,China)
Schrödinger equation foras non-Hermitian is given.Its nature,significance and application are discussed.
radiation damping;non-Hermitian;Schrödinger Equation
O157.5
A
1007-0834(2012)01-0001-04
10.3969/j.issn.1007-0834.2012.01.001
2011-12-14
国家自然科学青年基金项目(11102060);河南教育学院理论物理重点学科资助
马晓春(1962—),女,河南新乡人,郑州轻工业学院技术物理系高级工程师.
