基于非单调技术的ODE型算法
2012-12-23王冠舒
张 军,王冠舒
(海南大学信息科学技术学院,海南海口 570228)
基于非单调技术的ODE型算法
张 军,王冠舒
(海南大学信息科学技术学院,海南海口 570228)
将非单调技术与信赖域ODE算法相结合,提出了一种求解无约束优化的新算法,从而减少了迭代次数以及信赖域子问题的计算次数.并给出在一定条件下算法的整体收敛性,数值试验表明算法有效.
非单调技术;信赖域ODE算法;整体收敛;无约束优化
考虑无约束优化问题

其中,f是Rn→R的连续可微函数.
为了简便起见,在迭代点xk处,用表示欧式空间的,fk,gk分别表示f(xk),f(xk),Bk为Δ2f(xk)或其对称矩阵的一个逼近.
对于问题(1),文献[1]给出了一种信赖域ODE方法.ODE方法是沿着一个常微分方程组初值问题的解曲线寻找光滑函f(x)(xR)的极值点.其他介绍参见文献[2-3].
迄今为止,几乎所有的ODE型信赖域算法都是单调算法.然而,对于许多函数要求目标函数每一步严格单调下降会减缓收敛速率,尤其是当目标函数出现“锯齿”形状时候.文献[4]的数值实验表明,非单调技术比单调技术更具明显优势.
1987年,非单调线搜索方法是由GRIPPO L,LAMPARIELLO F和LUCIDI S[5]首次提出的.步长ak满足

1 算法及收敛性分析
受文献[5]中的算法启发,结合式(2)的非单调技术,提出了ODE改进算法.
算法1
步骤1 x0Rn,ε≥0,h0>0给定正整数M,B0=I,0<ρ0<1,k:=0.
步骤2 计算gk,若≤ε停止.
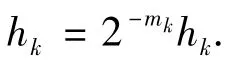
步骤4 求解下面线性方程组获得试探步dk.

步骤5 由式(2)求出fl(k),并计算fk+1及ρk,
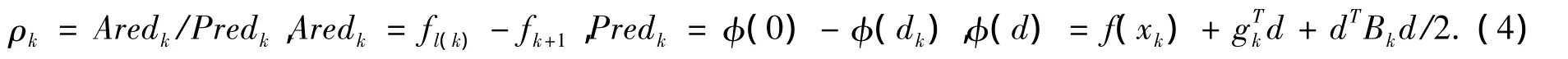
步骤6 若ρk<ρ0,hk=hk/2,转步骤4(内循环),否则转下一步.
步骤7 hk=2hk,xk+1=xk+dk,利用BFGS公式[4]得到Bk+1,k:=k+1(外循环).转步骤2.
为了得到全局收敛性,故作如下假设:
假设1f(x)在水平集L={x|f(x)≤f(x0)}有界.
假设2 Δf(x)是Lipschitz连续函数,即存在正常数L,满足

引理2[6]算法1产生序列{xk},当下降方向dk满足方程组式(3)的解时,有
1)当h<1/M时,此时,hBk+I正定.

定理1 在算法1以及引理2条件下,有
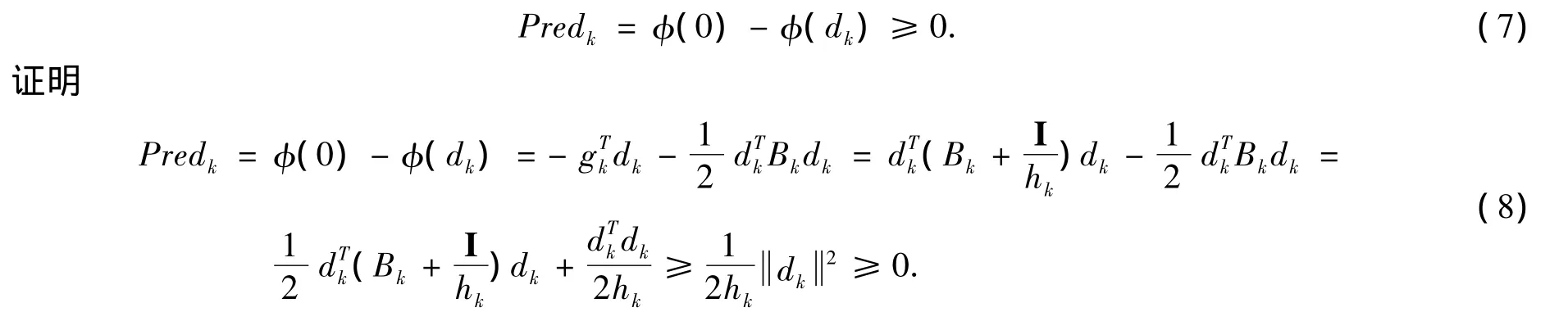
定理2 如果假设2、3成立,算法1的内循环迭代有限步终止,即步骤4、步骤5、步骤6循环是有限的.
由定理1知,

引理4[5]假设2、3成立,fl(k)满足式(2),则序列{fl(k)}单调递减且收敛.
定理3 如果假设1、2、3成立,算法1产生的序列{xk}满足:存在正整数k,gk=0.
情形1 假设存在{hk}的子列{hk}(子列仍然记为{hk}),∃h0>0,∀k>K,hk→0.类似于定理2的证明,可以得到当hk→0+,有pk≥p0,此时必存在某个正常数m,对任意的k>K,hk≥m,这与hk→0+矛盾.故情形1对于原命题成立.
情形2 假设∃h0>0,∀k,hk≥h0.因为
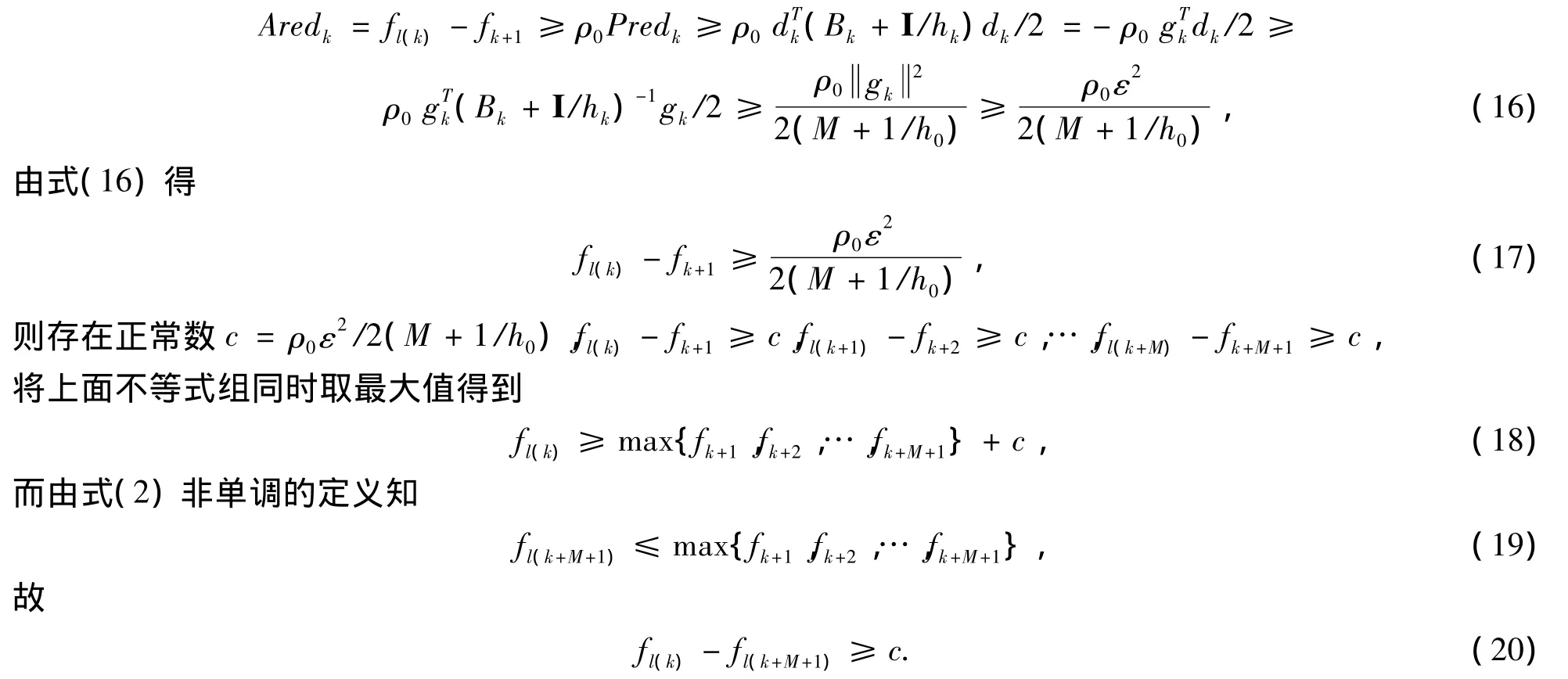
由定理4,将式(20)两端同时取极限得0≥c(矛盾),情形2原命题成立.得证.
2 数值实验
选取了文献[7]的15个标准函数进行了数值试验,并同文献[2]中的算法(M=0,记为TR-ODE)进行了比较,数值实验结果如表1所示,其中算法的程序设计语言是Matlab7.1,终止条件为 gk≤10-6,其余参数选取如下,B0=I(单位矩阵),ρ0=0.75,h0=1.
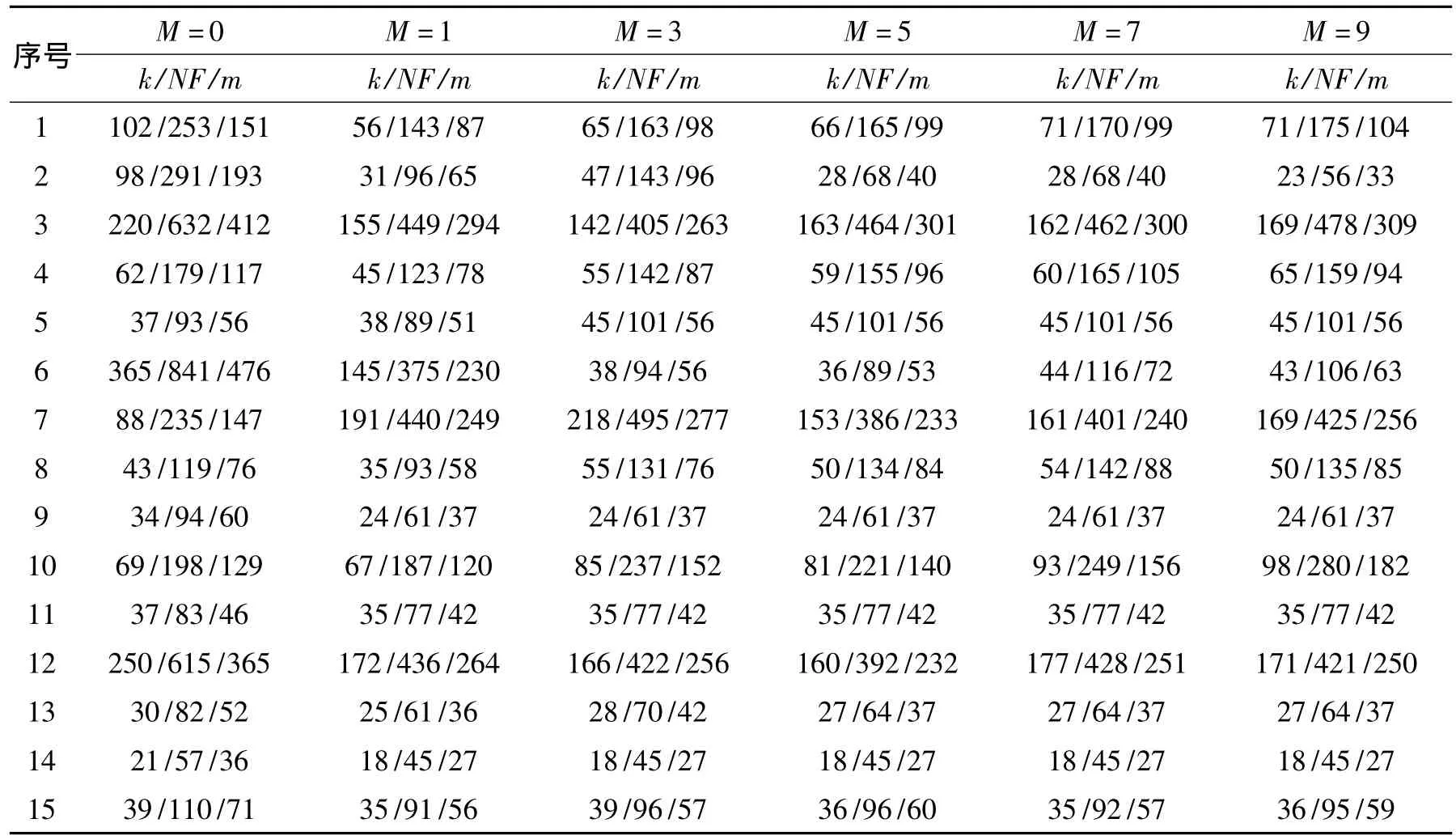
表1 不同M值的数值实验结果比较
表1中的数值结果表明,非单调算法优于单调算法.虽然非单调算法依赖M的选取,但非单调算法不失为一种有效的算法.
[1]BROWN A A,BIGGS M C.Some effective methods for unconstrained optimization based on the solution of systems of ordinary differential equations[J].Optim.Theory Appl,1989,62:211-224.
[2]OU Y G.A hybrid trust region algorithm for unconstrained optimization[J].Applied Numerical Mathematics,2011,61:900-909.
[3]OU Y G.A superlinearly convergent ODE-type trust region algorithm for nonsmooth nonlinear equations[J].Journal of Applied Mathematics&Computing,2006,22(3):371-380.
[4]DENG N Y,XIAO Y,ZHOU F J.A nonmonotonic trust region algorithm[J].Journal of Optimization Theory and Applications,1993,76(2):259-285.
[5]GRIPPO L,LAMPARIELLO F,LUCIDI S.A nonmonotone line search technique for Newton’s method[J].SIAM.Numer.A-nal,1986,23:707-716.
[6]HAN L X.关于无约束规划的一个ODE算法的收敛性质[J].计算数学,1992,15(4):449-455.
[7]ZHOU F J,XIAO Y.A class of nonmonotone stabilization trust region methods[J].Computing,1994,53:119-136.
Non-monotone ODE-type Trust Region Method
ZHANG Jun,WANG Guan-shu
(College of Information Science and Technology,Hainan University,Haikou 570228,China)
Non-monotone technology were combined with traditional trust region ODE-algorithm,and a new algorithm for unconstrained optimization problem were proposed,and which can reduce the number of iterations and trust region sub-problems number of calculation.Under certain assumptions,this paper also proved algorithm’s global convergence.Numerical results indicated that the proposed algorithm is effective and feasible.
non-monotonic technique;trust region ODE-algorithm;global convergence;unconstrained optimization
O 221
A
1004-1729(2012)01-0016-04
2011-10-06
海南省自然科学基金项目(111001)
张军(1986-),男,四川大竹人,海南大学信息科学技术学院应用数学系2009级硕士研究生.
