数学建模素质评估的定量分析
2012-12-23王浩华
王浩华,罗 婷
(海南大学信息科学技术学院,海南海口 570228)
数学建模素质评估的定量分析
王浩华,罗 婷
(海南大学信息科学技术学院,海南海口 570228)
针对海南大学学生参加数学建模竞赛的实际情况,应用层次分析法和动态规划的理论方法对数学建模队员的选拔问题进行了建模和分析.在兼顾公平选拔原则的基础上,对学生素质进行了综合评定,给出了最佳的分组原则.
层次分析法;动态规划;权重;组队原则
全国大学生数学建模竞赛已在各个高校中展开,并成为影响最大、参赛人数最多的大学生课外科技活动.海南大学1992年参赛以来,每次均取得了傲人的成绩.为了形成培训选拔机制,量化管理,优化参赛学生的质量以期取得更好的成绩,放眼未来,有必要对以前的工作做一些整理.为此,对海南大学学生在实际培训和选拔中就参赛队员各方面的素质予以评定,选取了选修笔试、机试、数学竞赛获奖、思维敏捷度、知识面、听课次数、其他情况等方面进行了考察(见表1),经量化评定给出了得分表(见表2).
1 模型假设
海南大学参赛学生主要来自于各个理工科学院,其教育背景和素质起点大致相当,故此,在整个参赛培训过程中假设各个队员遵循以下假设:
1)参赛队员的外部环境相同,且不受其他随机因素影响.在正式比赛的过程中,队员都能发挥正常水平.

表1 选拔学生信息
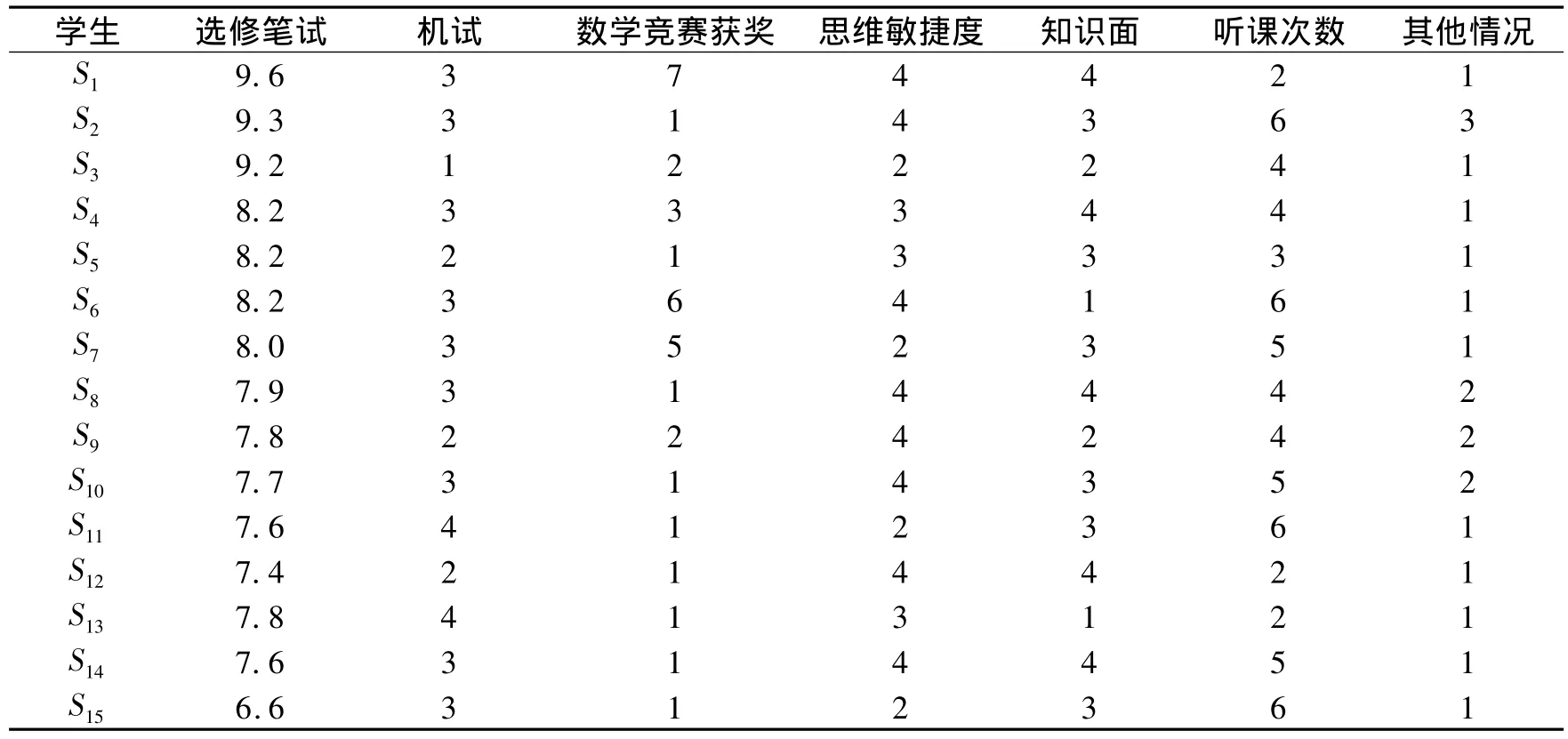
表2 量化评定得分表
2)竞赛水平的发挥只取决于表中所给的各项条件,且认为表2中测量的数据都是客观公正的.
3)数学建模选修成绩、机试成绩、数学竞赛获奖情况、思维敏捷程度、知识面宽广程度、数学建模选修课听课次数以及其他计算机应用情况,这7项对学生数学建模综合能力的影响占主要地位,且影响程度是依次递减的.
4)在组队后各队的发挥是相互独立的,不受其他组的影响.
5)组队后的整体水平由该队每项的最佳队员的指标表征.
2 参赛队员的选取
每个学生的基本条件由表1可知,该问题是半定量半定性、多因素的综合选优排序问题,是一个多目标决策问题.为了从15名队员中选出9名参赛者,主要利用层次分析法,分别计算各指标对选择队员的权重,以及各队员对各指标的权重,然后综合考察每个队员的权重并进行排名.
为了区分各项条件中的档次差异,首先将各指标量化,确定量化原则如下:
选修笔试成绩按照满分10分计;思维敏捷、机试和知识面的A,B,C,D等级分别按4分、3分、2分、1分计算;数学竞赛没获奖按1分来计算,获三等奖1次为2分,获三等奖2次为3分,获二等奖2次为5分,获一等奖1次为6分,获一等奖2次为7分;听课次数按一次1分计;其他情况如选修过MATLAB的加1分,通过计算机三级考试的加2分;班级排名情况由于统计数据不是很全面,所以不能进行量化,因此,这项指标可以不予考虑.
2.1 层次分析法 从15名学生中选拔9名优秀队员作为目标层,记为O;将刻画队员的7个指标作为准则层,记为C;将15名学生作为方案层,记为P;各队员记为Si,i=1,2,3…,15,如图1所示.
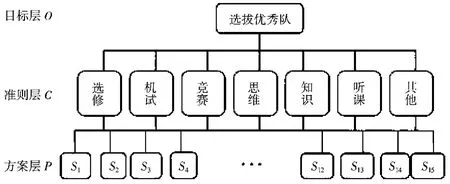
图1 层次结构图
由假设可得,准则层的7项指标依次递减,并认为相邻2项的差距不大,且都假设是相等的,这里都认为相差为1,于是两两对比得如下比较矩阵A.

其计算步骤如下:
步骤1 将A的每一列向量归一化得Vk(Tk,Xk);
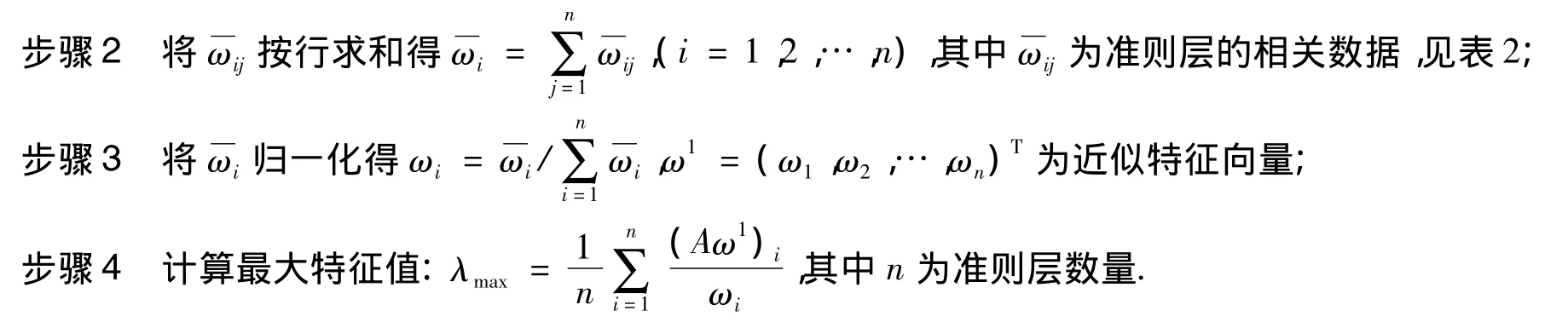
由以上步骤计算可得最大特征值λmax≈7.197 3,对应特征向量
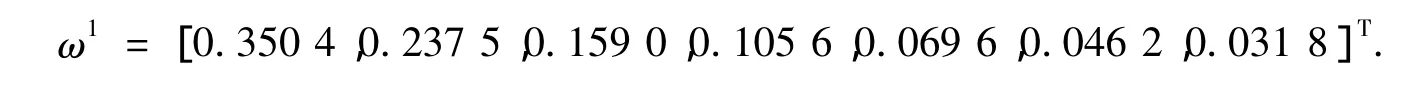
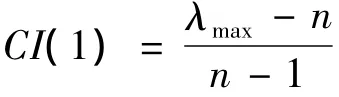

表3 随机一致性指标RI的值
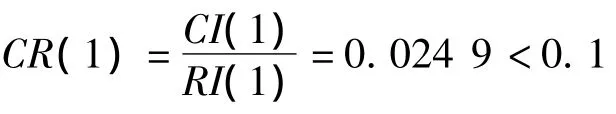

由于准则层C对目标层O的权重为ω1,方案层P对准则层C权重为ω2,则P对O的权重为
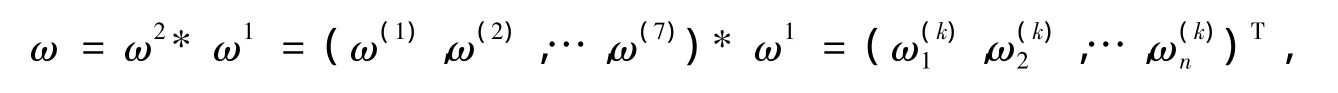
其组合一致性比率指标为
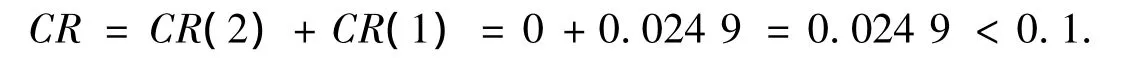
因此,组合权重ω可作为目标决策的依据.根据权重,得到15人的排序结果如表5所示.
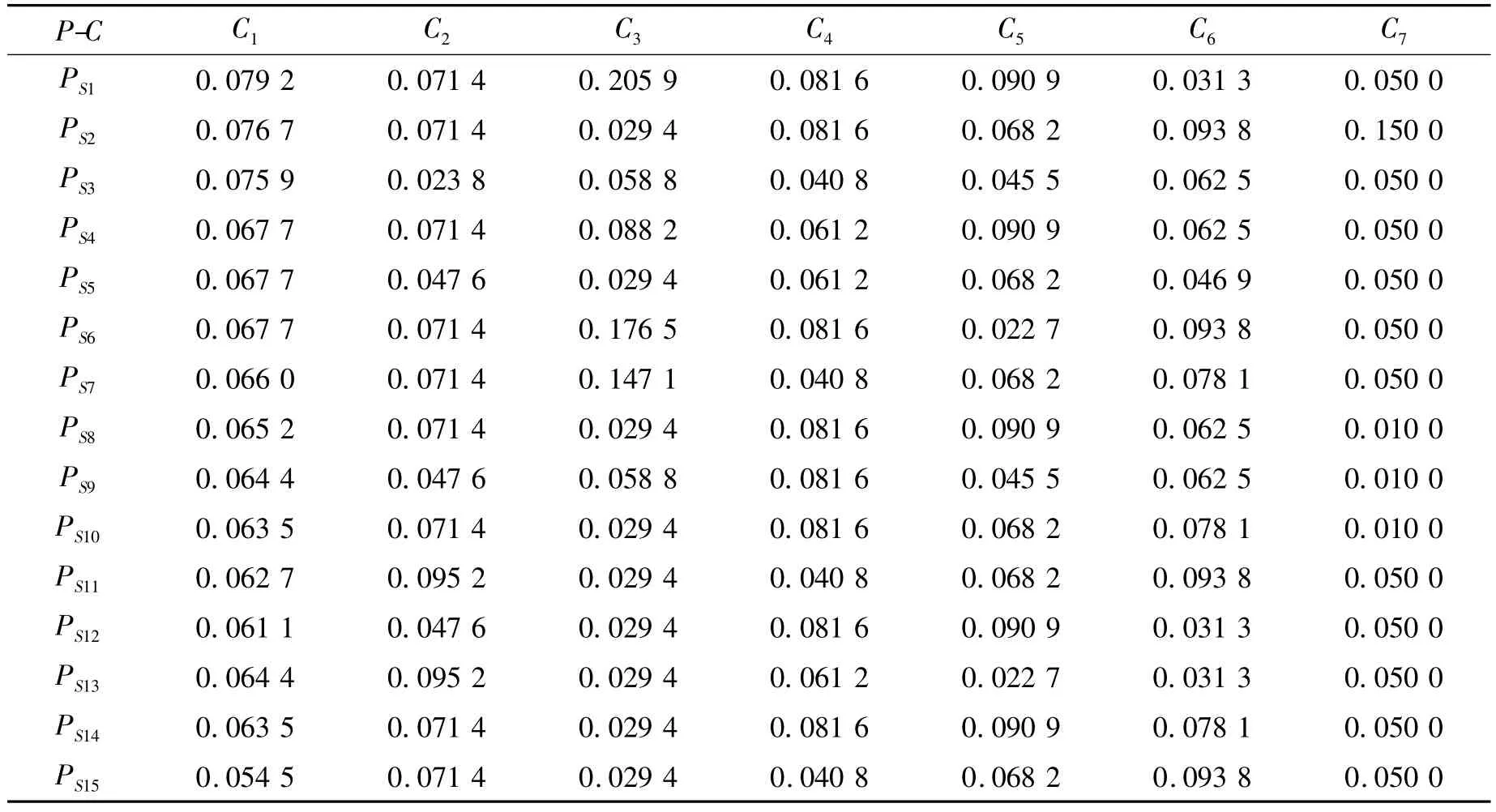
表4 P-C层的特征向量
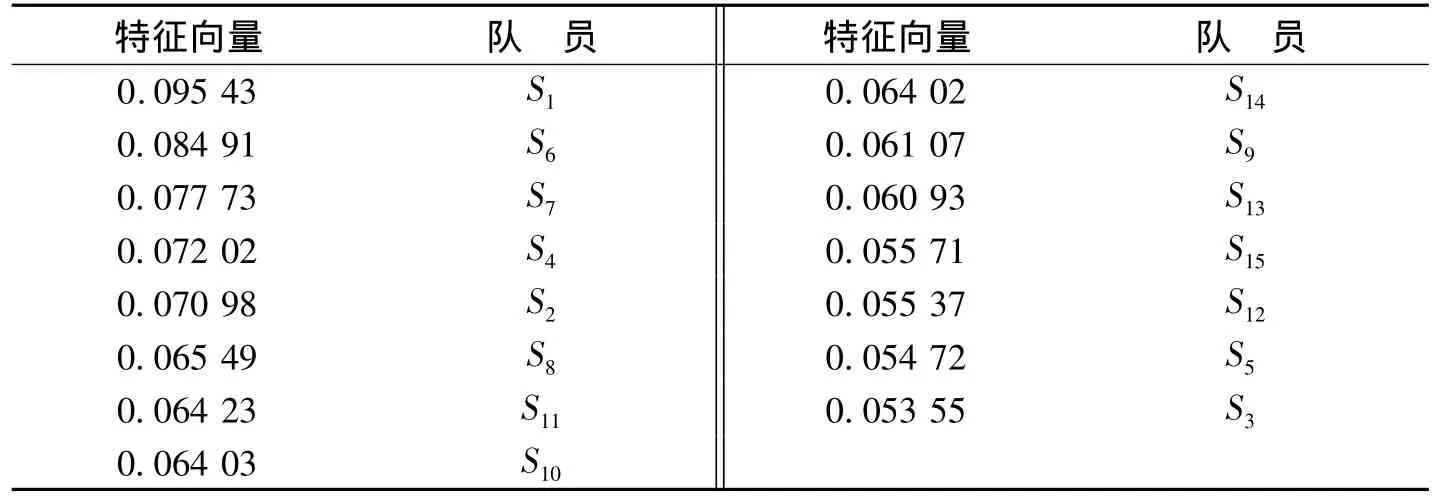
表5 15人的最终排序结果
其权重见图2.

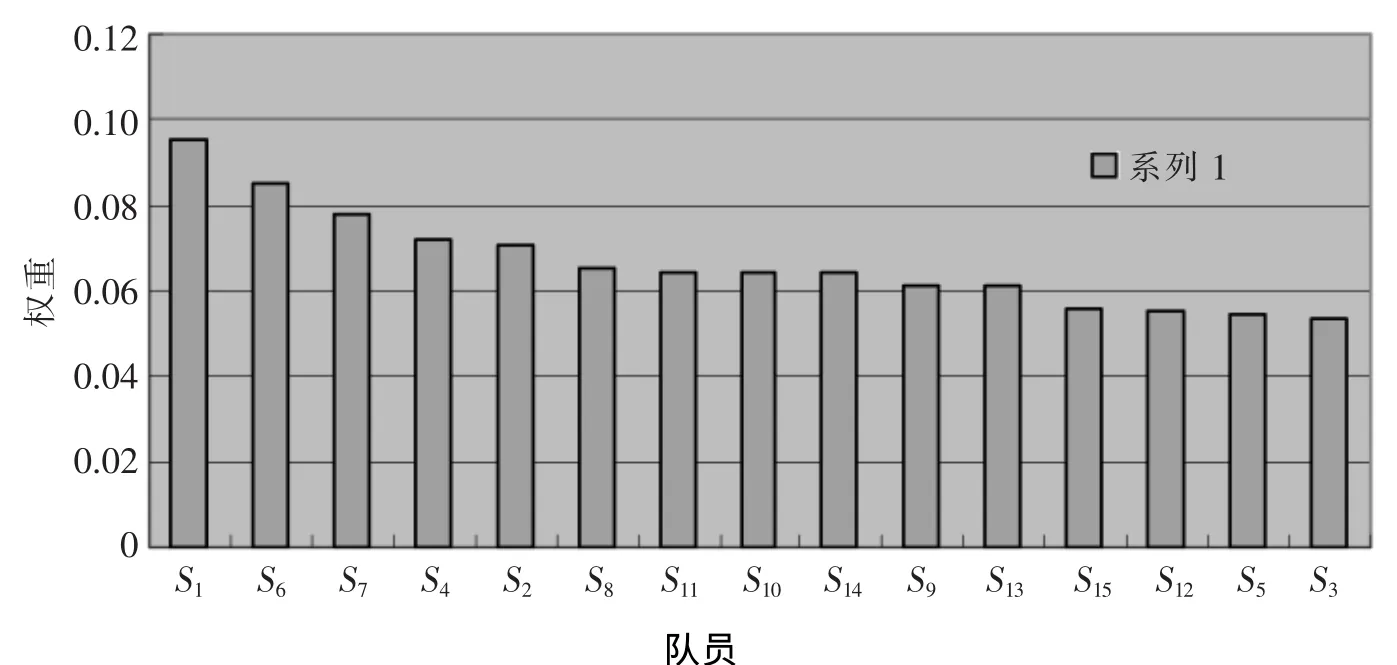
图2 15名队员权重图
故在15名学生中选取9名参赛队员,即可认为是选取权重排前9名的学生.由表5和图2可知,依次为:S1,S6,S7,S4,S2,S8,S11,S10,S14.
3 最佳组队方案的确定
3.1 组队原则
命题1[2]在最佳组队决策方案中,每个队对目标层O的权重一定不小于全体队员(9名)对目标层权重的几何平均值,否则其组队方案就不可能是最佳的.
由模型假设可知,各队员的组队原则遵循:
1)3名队员的技术水平指标可以互补,技术水平最高者为该队的水平指标;
2)按上述命题求出9名队员对目标层O权重的几何平均值,由表4按
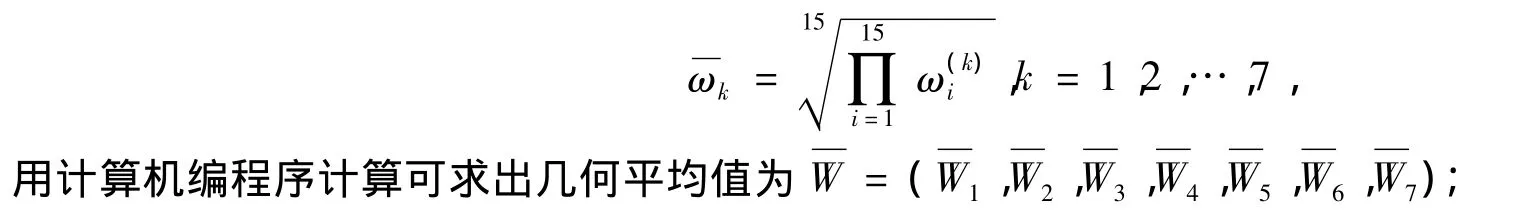
3)任取3名队员组合,求出相应的技术水平指标,取7个技术水平指标之和为最高组队方案.
3.2 最佳组队原则 设(x,y,z)三名队员组成的一个队,则mi(x)为队员x的第i项水平指标;Mi(x,y,
z)为队员x,y,z组队(x,y,z)的第i项水平指标;v(x,y,z)为技术水平指标,则
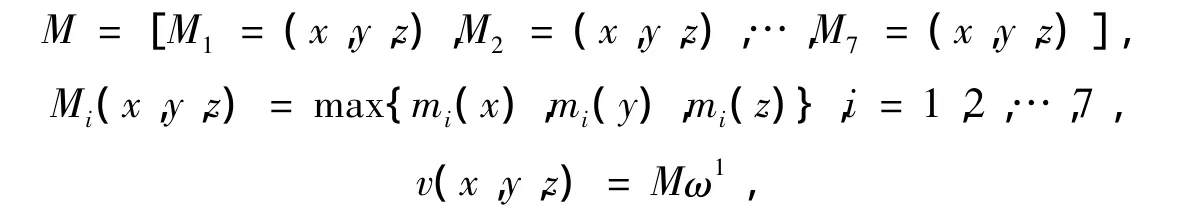
最佳组队是从15名队员中选出x,y,z,使v(x,y,z)最大.
3.3 建立模型 分决策过程为3个阶段,按组队原则完成,每一阶段确定一个队,记:
决策变量:Xk=(x,y,z)k,k=1,2,3;
状态变量:Tk,{k=1,2,3},其中T1={x1,x2,x3,x4,x5,x6,x7,x8,x9},即T1={S1,S2,S3,S4,S5,S6,S7,S8,S9};
状态转移方程:Tk+1=Tk-Xk,k=1,2,3;
允许决策集台:Dk={(x,y,z)∶x,y,z,vk(x,y,z)≥,k=1,2,3};
指标函数:Vk(Tk,Xk)表示决策(一个组队)关于状态的技术水平指标,即Vk(Tk,Xk)=M;
最优值函数:fk(Tk)表示在状态Tk下确定的k(1≤k≤3)个组队的技术水平指标之和的最大值,则有逆序解法的基本方程
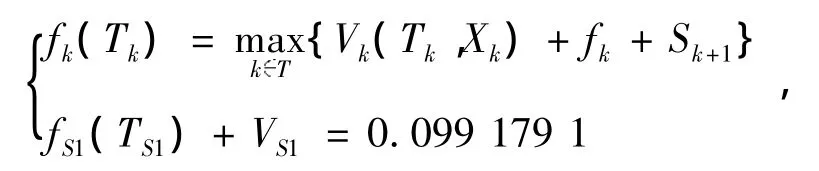
其中,Tk+1=Tk-Xk,k=1,2,3,经计算得出组队结果,见表6所示.

表6 最佳组队原则下组队结果
结合考察分组各队员专业情况,最终分组情况如表7所示.
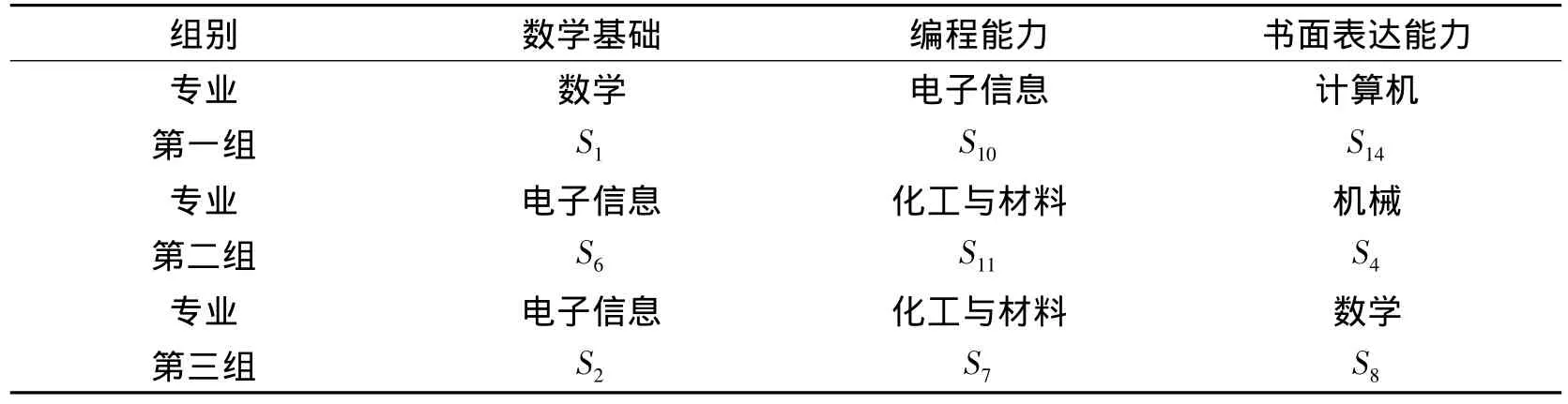
表7 组队结果与队员专业对比
由表7可以看出,此模型选拔和排队都达到了使每组有较好知识结构的目标.
3.4 模型的评价 采用随机挑选原则来组队,在15名队员中共有C315=455种不同的组合方式,目标函数为
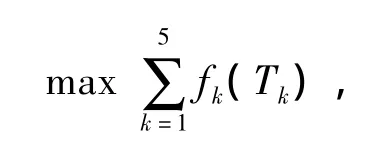
用MATLAB编程统计可知,可能构成组队的方式有448种,分3个阶段求解.
利用计算机将448种组合按权重的大小顺序排序,然后通过模拟枚举实验,得到最优决策方案和每一个队的竞赛水平,结果如表8所示.

表8 枚举法确定组队结果
从表6和表8可以看到,在所有的组队结果中最佳组队原则下的组队结果是最优的.
4 结束语
一年一度的全国大学生数学建模竞赛是高等院校的重要赛事,指导教师应本着对全校学生负责的态度,公平公正地对参赛队员进行选拔.学校要加大宣传力度,进一步扩大选拔范围,使更多的优秀同学参赛,从而更好地优化和完善参赛队伍结构.同时也要加大投入力度,如师资和资金投入等.
学生数学素质的培养不是一朝一夕的事情,因此,教师要始终把数学建模意识贯穿于教学的全过程,尤其是要把数学建模思想和方法渗透到数学主干课程的教学中,只有这样,才能更好地把数学建模教学活动与数学教学改革融为一体,才能真正地提高教学质量,并使广大学生受益.
附录程序1


[1]姜启源.数学模型[M].第3版.北京:高等教育出版社,2003.
[2]韩中庚.最佳组队方案及模型[J].数学的实践与认识,1997,27(2):133-140.
[3]刁在筠.运筹学[M].第3版.北京:高等教育出版社,2007.
[4]李志林,欧宜贵.数学建模及典型案例分析[M].北京:化学工业出版社,2008.
Quantitative Analysis of Quality Assessment about Mathematical Modeling
WANG Hao-hua,LUO Ting
(College of Information Science and Technology,Hainan University,Haikou 570228,China)
Based on the actual situation of mathematical modeling contest of Hainan University,Analytic Hierarchy Process(AHP)and the dynamic programming theory were used to construct the mathematical model for selecting the team member.Based on the principle of fairness,the students were evaluated and the best grouping principles were proposed.
AHP;dynamic programming;weight;grouping principle
O 221.3
A
1004-1729(2012)01-0009-07
2011-06-17
海南省教育厅高校科研资助项目(Hjsk2011-23);海南大学教育教学科研资助项目(hdjy1005)
王浩华(1981-),男,湖北天门人,海南大学信息科学技术学院讲师,硕士.
