双种群进化粒子群算法求解地下水管理模型

吴睿奇，朱国荣，王 佩

(南京大学地球科学与工程学院，江苏 南京 210093)

双种群进化粒子群算法求解地下水管理模型

吴睿奇，朱国荣，王 佩

(南京大学地球科学与工程学院，江苏 南京 210093)

为避免粒子群算法(PSO)早熟的缺点，设计了一种双种群进化粒子群算法(DE-PSO)。DE-PSO是基于PSO，引入选择、交叉及差分变异操作，并结合合理有效的粒子评价方法及越界处理方法之后形成的。将DE-PSO应用于两个地下水管理模型算例，第一个算例DE-PSO解的总抽水量分别比遗传算法(GA)、模拟退火算法(SA)和PSO减少了64、256、207 m3/d，第二个算例DE-PSO解的总治理成本分别比GA、SA和PSO减少了57.74、151.93、76.59万元。两个算例中DE-PSO都表现出稳定的进化趋势，寻优效率好于GA、SA和PSO，可以有效求解地下水管理模型问题。

地下水管理模型;粒子群算法;双种群;差分变异

0 引言

地下水管理模型是实现地下水科学管理的有力工具(于福荣等，2010)，其实质是寻求以最少的社会经济环境成本(包括安装井、抽水和治理污染等方面)来满足既定管理目标(Wanger，1995)。目前，求解地下水管理模型的方法包括传统优化算法和智能算法。传统优化方法包括线性规划(LP)和非线性规划(NLP)，前者只能求解目标函数和约束条件都是关于决策变量的线性函数的问题，后者要求目标函数和约束条件连续、可导，而且容易陷入局部最优;智能算法包括遗传算法(GA)、模拟退火算法(SA)、禁忌搜索(TS)等，这些智能算法具有启发式寻优特点，已被应用于地下水优化管理中，但由于所有智能算法都基于随机搜索，无法确保获得全局最优解，因此如何提高全局寻优能力仍是这些智能算法的改进方向。

粒子群算法(PSO)由 Kenney和 Eberhart于1995年提出，是基于群智能的随机全局优化技术，具有控制参数少、收敛快、原理简单等优点。然而，PSO容易早熟且在处理约束优化时存在粒子越界飞行问题。目前，许多学者进行了传统PSO的改进研究，提出了下列具体改进方法。①基于PSO公式中控制参数的改进。② 借鉴遗传算法，引入选择、交叉、变异(高斯变异、柯西变异、差分变异等)操作。③设立不同层次、功能的子种群。④ 将PSO与GA、SA、TS、模式搜索等算法嵌套成混合智能算法。⑤将PSO模型看成一种热力学系统，引入热力学思想。⑥基于粒子评价方法和越界处理方法的改进(针对约束优化)。⑦ 以上方法的综合。综合考虑不同改进方法的复杂程度及有效性，笔者对PSO作了3个方面的改进。①设立2个平行的子种群进行优化，2个子种群通过粒子更新公式及选择、交叉操作交流信息。②对粒子更新公式作了调整，舍弃了惯性项，使粒子速度不再有继承性，修正了粒子学习机制，使其不仅可以向自身个体历史极值和整个群体的历史极值学习，同时也向粒子所在子种群的历史极值学习，并接受邻群粒子的随机差分变异扰动。③采用合理的粒子评价方法和越界处理方法，使其更适于求解约束优化。经过上述改进的算法借鉴了GA中生物进化(选择、交叉、变异)思想，称为双种群进化粒子群算法(DE-PSO)，DE-PSO避免了PSO的早熟缺点，提高了全局寻优能力。

1 地下水管理模型

地下水管理模型由水流模型、溶质运移模型及优化模型耦合而成。前者用来不断更新状态变量，包括地下水流运动模型和溶质运移模型;后者用来选择最优决策变量。状态变量通常指水头和溶质浓度;决策变量包括抽水量(注水量)、井的数目、井的位置、治理周期末污染物的总量，还可能包括每口井的“开/关”状态等(杨蕴等，2009)。

1.1 水流模型和溶质运移模型

假设水的密度为常数，当各向异性介质的主方向与坐标轴的方向一致时，三维地下水流的运动方程可表示为：

不考虑吸附作用及化学反应，描述三维非稳定渗流系统中的溶质运移的方程可表示为：

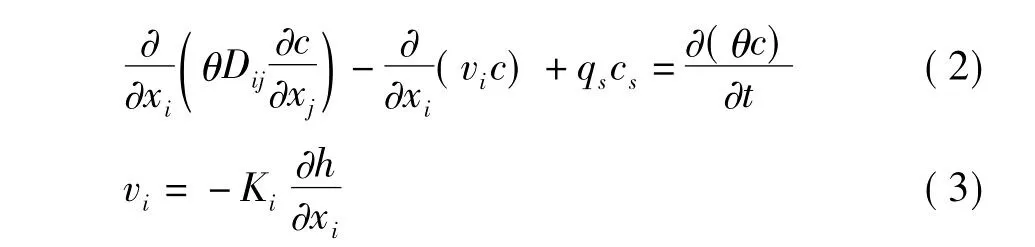
式(1)、(2)、(3)中：Ki为渗透系数张量在 i方向的主值(LT-1);b为含水层饱和带厚度(L);h为水头(L);qs为源汇项(LT-1);μ为给水度(无量纲);t为时间(T);c为溶质体积质量分数(ML-3);Dij为水动力弥散系数(L2T-1);cs为源或汇组分中的溶质体积质量分数(ML-3);θ为含水介质的孔隙度;νi为地下水沿不同方向i的达西流速(LT-1)。

式(1)与相应边界条件及初始条件结合构成水流模型。式(2)为溶质运移基本方程，其中的达西流速vi通过式(3)求得，而式(3)中的水头h通过式(1)求得。因此，溶质运移模型是由式(1)—式(3)与相应边界条件及初始条件构成。

1.2 优化模型

优化模型由目标函数及约束条件组成，目标函数通常是总的价格、总的抽水量或总的抽出污染物质量等。约束条件通常包含水位约束、水力梯度约束、浓度约束和流量约束等(杨蕴等，2009)。

2 双种群进化粒子群算法(DE-PSO)求解地下水管理模型

2.1 粒子群算法(PSO)

粒子位置和速度根据以下公式进行更新：

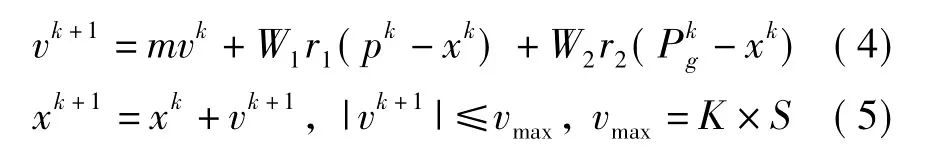
式(4)、(5)中：vk为第k次迭代的粒子速度，xk为第k次迭代的粒子位置;Pk为第k次迭代粒子历史最优解，P为第k次迭代群体历史最优解;m为惯性权重，W1、W2为学习因子1和学习因子2，常取W1=W2=2.0;vmax表示粒子最大速度，K为系数，一般取0.1～1.0;S为粒子位置最大变化幅度，其值等于上下边界值之差;r1和r2为0～1均匀分布的随机数。

2.2 双种群进化粒子群算法(DE-PSO)

基于子种群思想，DE-PSO设置两个平行的子种群1和2进行优化，子种群1和2的群体规模一致，两个子种群的粒子同步进化，其粒子更新公式、粒子评价方法及越界处理方法一致。子种群间通过粒子更新公式和选择、交叉操作交流信息。

2.2.1 引入差分变异的粒子更新公式 PSO中惯性权重的确定没有普适的方法，对于复杂的非线性优化问题，即使采用自适应方法调整惯性权重，搜索精度提高效果也不明显(罗德相，2009)。许多研究者发现PSO算法中速度的概念并不是必须的，徐星等(2011)取消了粒子速度的概念，保留了PSO的学习机制。笔者设计的DE-PSO虽保留了粒子速度概念，但取消了惯性权重;粒子速度无需初始化，且不再具有继承性。差分变异算子对粒子群算法性能的改进有很大的促进作用。因此，DE-PSO将其引入到粒子更新公式中，改进后的DE-PSO粒子更新公式为：

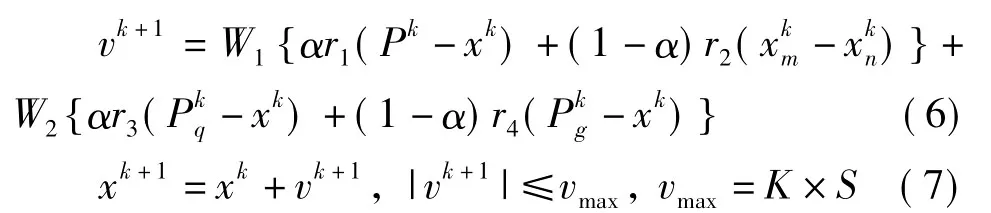
式(6)、(7)中：α为分配系数，取值在0～1之间，经实验α取0.5较合适;X、X为从邻群中随机选择的两个不同粒子;P表示第k次迭代整个群体(包含两个子种群)的历史最优解，P表示第k次迭代粒子所在子种群的历史最优解;r1、r2、r3、r4为0～1均匀分布的随机数;其余符号含义同式(4)、式(5)。

2.2.2 选择与交叉操作 选择操作可以不断淘汰较差的粒子，使算法对于当前较好区域有更好的开发能力;而交叉操作与子种群结合，可以使粒子受益于父母双方，增强搜索能力，易于跳出局优(汪定伟等，2007)。DE-PSO在每次粒子评价结束后，分别对两个子种群的粒子进行排序，选择两个子种群中较好的一半粒子作为父代粒子。设子种群的群体规模均为N，按公式(8)进行N次交叉操作，所得2N个子代粒子最后放回子种群1和2，取代原来粒子构成新种群。

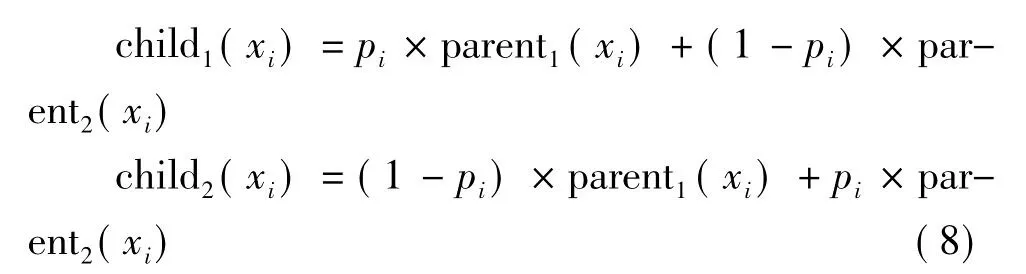
式中：parent1和parent2表示父代粒子，分别随机选自子种群1和2，且是所在子种群排名前N/2的粒子;child1和child2表示由父代粒子 parent1和 parent2交叉产生的两个子代粒子，分别被放回子种群1和2;xi表示粒子第i维的值;pi为0～1均匀分布的随机数。

2.2.3 粒子评价与越界处理 当粒子违反约束条件时，一般可以采用罚函数法或拒绝策略，罚函数法会限制算法求解精度，拒绝策略则很难执行，因为对于一个复杂问题，即使重复多次初始化也很难获得较多的可行解，完全摒弃或不评价不可行解将导致优化难以进行(汪定伟等，2007)。刘衍民等(2011)根据粒子违背约束条件的程度，提出一种新的粒子间比较准则，DE-PSO借鉴其思想进行粒子评价。设有两个粒子X、Y，则在以下两种情况下DE-PSO判定X比Y更优：①约束条件的满足个数相同，但X的目标函数值比Y小(最小值问题);②X约束条件的满足个数比Y多。

PSO在处理约束问题时，决策变量越界是经常发生的，目前，处理粒子越界主要有吸收墙、反射墙、不可见墙3种方法，吸收墙和反射墙能使粒子达到边界值，但同时会加大算法在边界附近陷入局优的风险，不可见墙降低了算法在边界附近的早熟风险，但会导致边界值不可到达，也会导致额外升级和进化不均。DE-PSO对越界粒子作如下处理：若粒子在某维越界前的取值与边界的差值很小，则判定粒子原本就处于边界附近，采用吸收墙办法，将其值设为边界值，反之判定粒子在该维的更新无效，粒子在该维与当前群体历史最优解进行交叉操作，具体越界处理公式为：

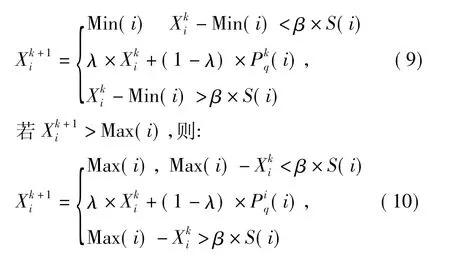
2.2.4 DE-PSO算法步骤 ①初始化粒子位置、个体极值、子种群极值及群体极值。②分别对两个子种群的粒子进行排序，按式(8)执行选择、交叉操作(完成一次迭代)。③按式(6)—(7)更新粒子位置(进入新的迭代)，如有越界按式(9)—(10)处理。④评价粒子，更新个体极值、子种群极值及群体极值。⑤判断是否满足迭代终止条件(或达到最大迭代次数)，如满足，算法终止，输出群体极值，否则转②继续优化。

3 算例研究

3.1 水头约束问题

3.1.1 问题概述 算例改编自文献(于福荣等，2010)，如图1所示，某均质、各项同性承压含水层中拟设9口抽水井用于疏干建设区内的地下水，使得建设区范围内的地下水位降至50 m以下。含水层底板水平;南北部为隔水边界;东西部为一类边界，给定水头值分别为60 m和80 m;地下水流为二维稳定流，含水层导水系数为 50 m2/d，采用MODFLOW模拟水流。每口井的最大抽水量为3 000 m3/d。用边长为100 m的正方形网格将研究区剖分为20行、30列的网格。

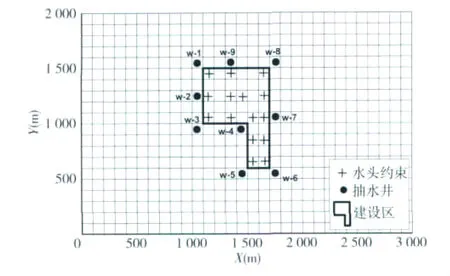
图1 水头约束问题研究区示意图

约束条件：

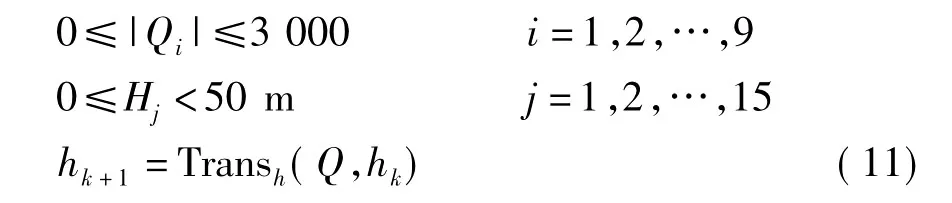
式中，J为目标函数，为总抽水量(m3/d);Qi为井i的抽水量(m3/d);Hj表示水头约束点j的水头;hk+1表示研究区地下水在k+1时段的水头分布;Transh代表水头由k时段到k+1时段的状态转移函数;Q为决策变量，Q=［Q1，Q2，Q3，…，Q9］。

分别用GA、SA、PSO及笔者提出的DE-PSO求解算例，其中PSO对约束条件及越界的处理与DE-PSO一致。GA参数为：编码长度45，交叉概率0.5，变异概率0.01，种群规模100，最大迭代次数100。SA参数为：每个变量的离散化区间数为32，邻域搜索决策变量单步长中增加量为1，初始温度e10，衰减因子0.75，每个T值的迭代次数为100，外循环最大迭代次数为100。PSO参数为：W1=W2=2.0，m=0.5，K=0.1，β =0.01，种群规模 100，最大迭代次数为100。DE-PSO参数为：W1=W2=2.0，α=0.5，K=0.1，β=0.01，两个子种群规模均为50，最大迭代次数为100。

3.1.2 优化结果对比 表1为优化结果对比表，其中，与GA、SA及PSO解相比，DE-PSO解得到的总抽水量最少，分别比GA、SA和PSO减少了64、256、207 m3/d。将几种智能算法解代入水流模型，发现所有解均满足约束条件。图2为相应的地下水位等值线优化结果图，其中，DE-PSO地下水位等值线图中50 m等水位线所包围的区域集中在建设区附近。图3对比了各智能算法运行时，10～100代最优解总抽水量的变化趋势。由图3可知，PSO进化缓慢，近于停滞;GA、SA在相同迭代次数下的总抽水量总体高于DE-PSO;DE-PSO曲线呈较稳定的下降趋势，寻优效率最好，分析其原因在于DE-PSO引入的选择、交叉及差分变异操作避免了PSO的早熟现象。

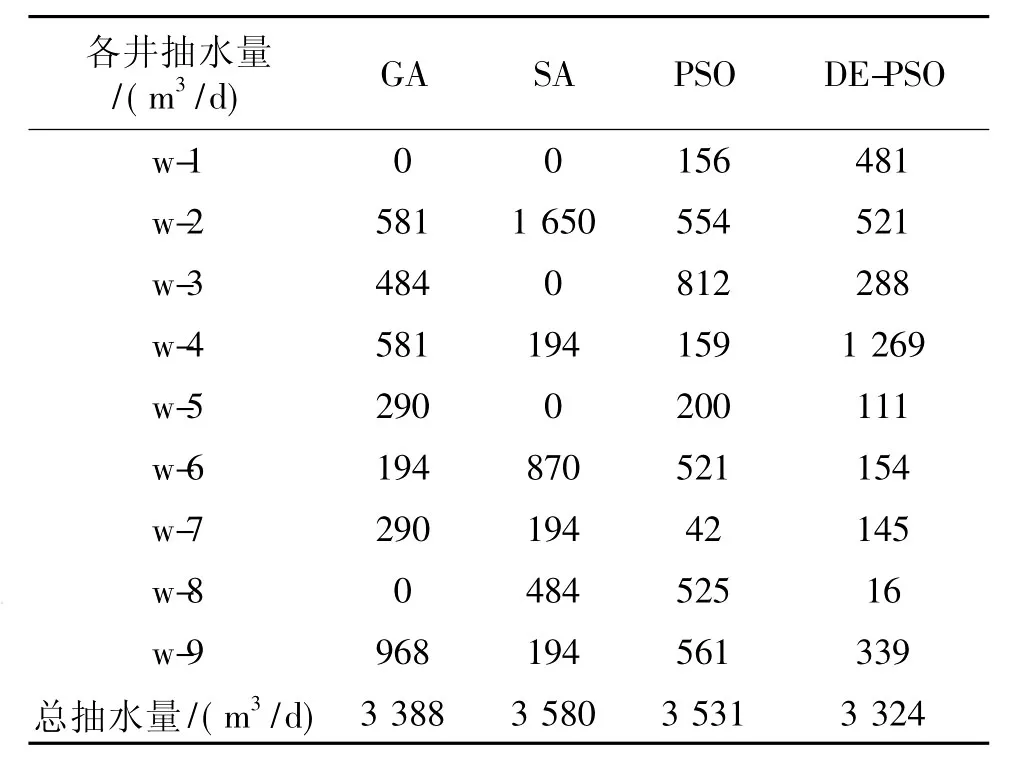
表1 水头约束问题优化结果对比

3.2 质量分数约束问题

3.2.1 问题概述 算例选自文献(徐星等，2011)如图4所示，一承压含水层存在硝酸盐(以氮计)污染，拟用抽出处理方法治理，治理周期为5 a，4口预选治理抽水井的位置已在图中标出。水流模型为二维非稳定流模型。研究区南北部为隔水边界，东西部为定水头边界，水头值分别为25 m和35 m;研究区西部、北部和南部为溶质零通量边界，东部为溶质对流给定通量边界。用边长为150 m的正方形网格将研究区剖分为17行23列有限差分网格，采用MODFLOW模拟流场，MT3DMS模拟质量分数场。模型设1个应力期，5个时间步长，每个时间步长进一步被分解为若干个运移步长。模型用到的水文地质参数：孔隙度为0.2，导水系数为500 m2/d，贮水系数为0.000 1，纵向弥散度为50 m，横向弥散度为10 m。管理模型为：

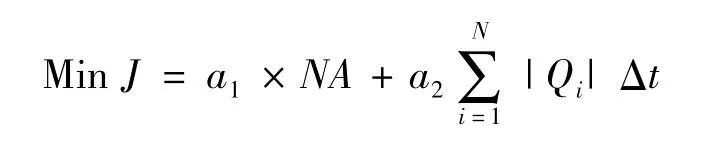
约束条件：

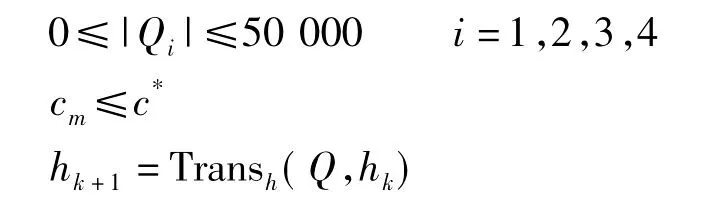
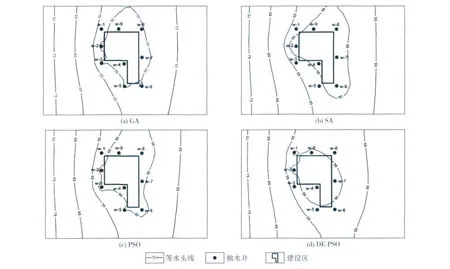
图2 水头约束问题地下水位等值线优化结果图

图3 水头约束问题各智能算法的迭代运行

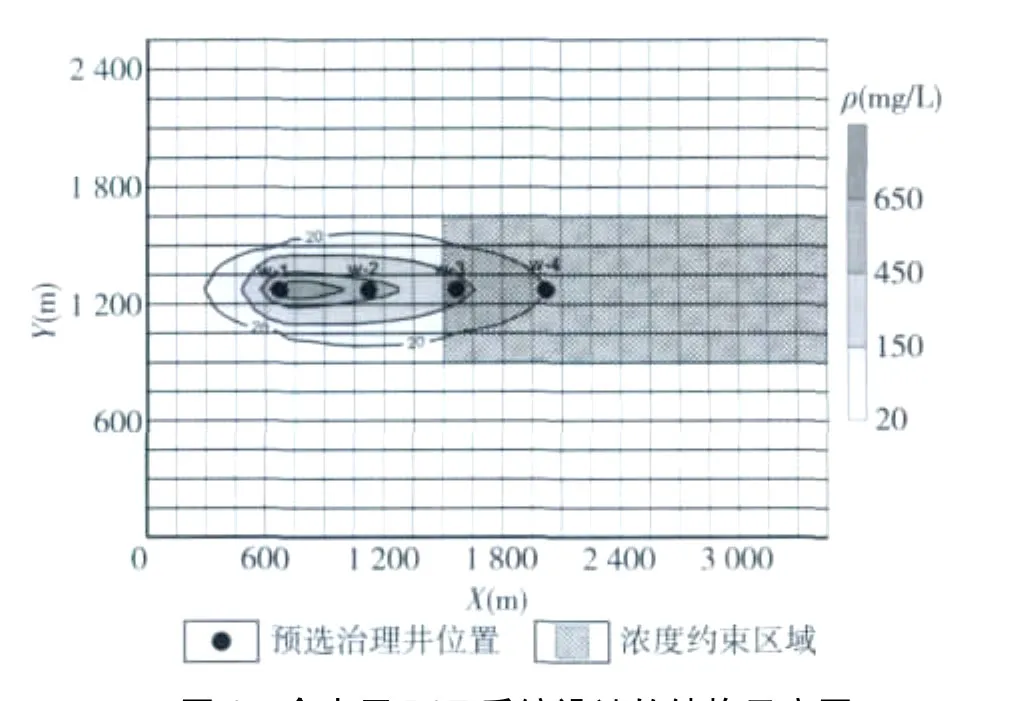
图4 含水层PAT系统设计的结构示意图

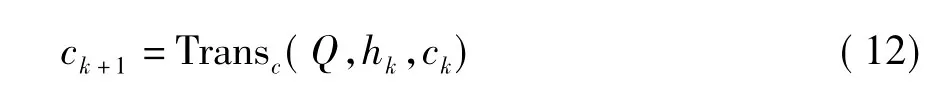
式中，J为目标函数，为总治理成本;NA为非零流量井的数目;N为总的优选井的数量;a1为安装井的费用系数，算例中单口井安装费用10万元;a2为处理费用系数，算例中取0.8元/m3;Qi为井i的抽水量(m3/d);cm是治理周期末体积质量分数约束区域任意一点的溶质体积质量分数(mg/L);c*为治理周期结束后体积质量分数约束区域的体积质量分数约束条件(mg/L)，算例中设置为20 mg/L，即达到地下水III类水标准;hk+1、ck+1分别表示研究区地下水在k+1时段的水头和溶质体积质量分数分布;Transh，Transc分别代表水头和溶质体积质量分数由k时段到k+1时段的状态转移函数;Q为决策变量，Q=［Q1，Q2，Q3，Q4］。

分别用GA、SA、PSO及笔者提出的DE-PSO求解算例，其中PSO对约束条件及越界的处理与DE-PSO一致。GA参数为：编码长度20，交叉概率0.5，变异概率0.025，种群规模40，最大迭代次数50;SA参数为：每个变量的离散化区间数为32，每个T值的迭代次数40，外循环最大迭代次数50，其他参数值同算例1;PSO参数为：种群规模40，最大迭代次数50，其他参数值同算例1;DE-PSO参数为：两个子种群规模均为20，最大迭代次数50，其他参数值同算例1。

3.2.2 优化结果对比 表2为优化结果对比。其中，DE-PSO解得到的总治理成本最少，分别比GA、SA和PSO减少了57.74、151.93、76.59万元。

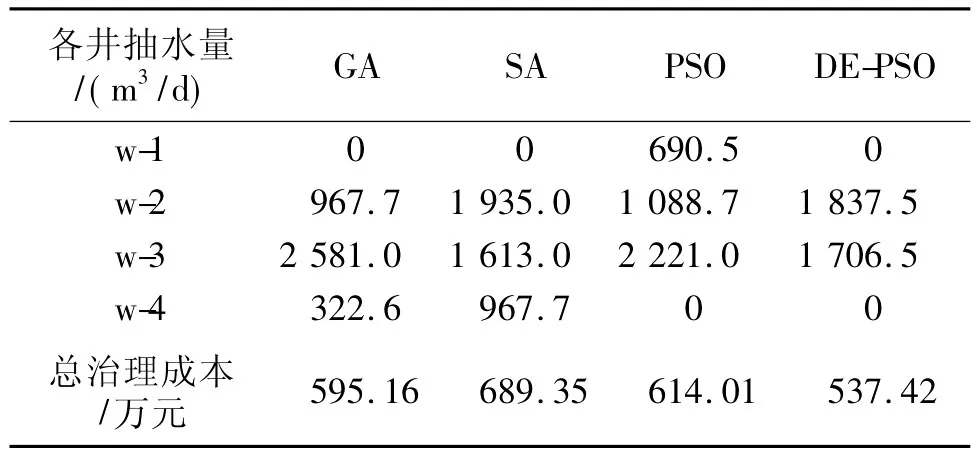
表2 浓度约束问题优化结果对比

图5对比了各智能算法运行时，10～50代最优解总治理成本的变化趋势，其中GA、SA、PSO在相同迭代次数下的总治理成本总体高于DE-PSO，DE-PSO曲线呈较稳定的下降趋势，寻优效率最好，避免了PSO的早熟现象。

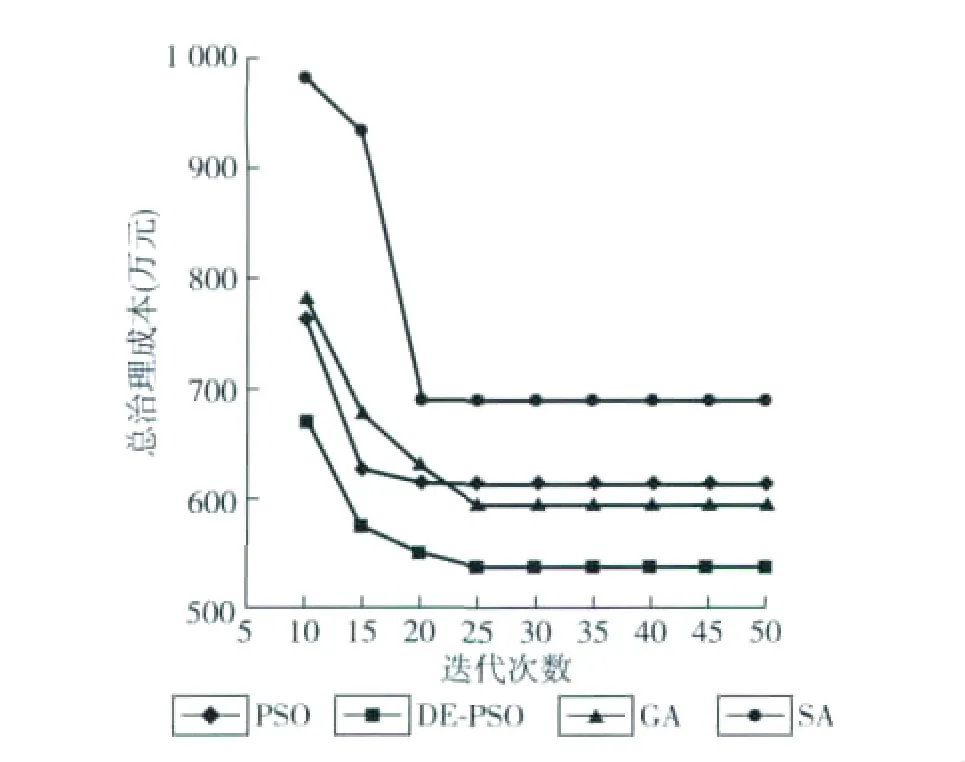
图5 质量分数约束问题各智能算法的迭代运行

4 结论

(1)基于PSO算法，设立了两个平行子种群进行优化，增加选择、交叉操作，在粒子更新公式中引入差分变异操作，并采用有效的粒子评价、越界处理方法，提出DE-PSO算法。

(2)算例模拟结果表明：DE-PSO对PSO作改进后，增强了全局寻优能力且进化稳定，克服了PSO的早熟缺点，优化结果及寻优效率优于GA、SA及PSO，适于求解地下水管理模型。

李相勇，田澎，孔民.2007.解约束优化问题的新粒子群算法［J］.系统管理学报，16(2)：120-129.

刘衍民，隋常玲，牛奔.2011.解决约束优化问题的改进粒子群算法［J］.计算机工程与应用，47(12)：23-26.

罗德相.2009.粒子群算法改进方法研究［D］.广西：广西民族大学.

汪定伟，王俊伟，王洪峰，等.2007.智能优化方法［M］.北京：高等教育出版社.

吴蓉，周志芳.2002.改进的前馈型神经网络模型在承压水漏斗水位预报中的应用［J］.地质学刊(原《江苏地质》)，26(1)：19-21.

徐星，李元香，吴昱.2010.基于扩散机制的双种群粒子群优化算法［J］.计算机应用研究，27(8)：2882-2898.

徐星，吴昱，李元香.2011.基于布朗运动的改进粒子群算法［J］.计算机应用研究，28(7)：2439-2442.

杨蕴，吴剑锋，吴吉春.2009.两种智能算法在求解地下水管理模型中的对比［J］.吉林大学学报：地球科学版，39(3)：474-481.

于福荣，卢文嘉，李平，等.2010.地下水管理模型求解方法综述［J］.水文地质工程地质，37(2)：27-31.

AHLFELD D P，MULLIGAN A E.2000.Optimal management of flow in groundwater systems［M］.San Diego：Academic Press.

MCKINNEY D C，LIN M D.1995.Mixed-integer nonlinear programming methods for optimal aquifer remediation design［J］.Water Resources Research，31(3)：731-740.

WANGER B J.1995.Recent advances in simulation optimization groundwater management modeling［J］.Review of Geophysics，(Suppl)：1021-1028.

Double-population evolution-particle swarm optimization algorithm for solving groundwater management model

WU Rui-qi，ZHU Guo-rong，WANG Pei

(School of Earth Sciences and Engineering，Nanjing University，Nanjing 210093，China)

To solve the premature convergence problem of Particle Swarm Optimization(PSO)，a new algorithm named DE-PSO(Double-population Evolution-Particle Swarm Optimization)was designed.DE-PSO introduced selection，crossover and differential mutation into PSO，and adopted a new evaluation method to evaluate swarms and a new control method to ensure all swarms can fly inside search space.DE-PSO was applied to solve two groundwater management cases.In the first case，DE-PSO produced a design with respectively 64，256 and 207 m3/d less pumping rate than those of GA 、SA and PSO;in the second case，DE-PSO produced a design with respectively ¥577，400，¥1，519，300 and ¥765，900 less remedial design cost than those of GA，SA and PSO.Two case studies indicated that DE-PSO could evolve steadily，the searching efficiency was better than GA，SA and PSO.DE-PSO could solve groundwater management model problems effectively.

Groundwater management model;Particle swarm optimization;Double population;Differential variation

TP18;P641.8

A

1674-3636(2012)01-0037-07

10.3969/j.issn.1674-3636.2012.01.37

2011-10-26;编辑：陆李萍

国家自然科学基金项目(J0830522)资助

吴睿奇(1988— )，女，硕士研究生，水文与水资源专业，E-mail：gwflow@nju.edu.cn