基于物理模型的水泵寿命评估
2012-12-21刘锐,黄政,白云
刘 锐,黄 政,白 云
(海军工程大学船舶与动力学院,湖北 武汉 430033)
离心泵是船舶辅机的重要组成部分,以其转速快、体积相对较小、净质量小、效率高等特点,在现代船舶上有着十分广泛的应用。但随着高流量、高扬程离心泵的应用,对离心泵的可靠性提出了更高的要求。因此研究离心泵的可靠性,合理评估其寿命,对制定适宜的维修策略非常重要,有利于最大限度发挥其经济效益。
离心泵常常因流量不足而发生故障。流量过小,泵内温升过大,使介质过早气化而导致气蚀。气蚀会使材料损坏,振动和噪声加剧,流量、压头和效率明显下降,甚至发生断流现象。因此本文基于流量与间隙的物理关系模型,以保证离心泵运行时不发生气蚀的最小流量为可靠度指标,根据影响间隙变化的退化因素,建立了离心泵的寿命评估模型。
1 寿命评估模型的建立
对于离心水泵,其流量公式为[1]
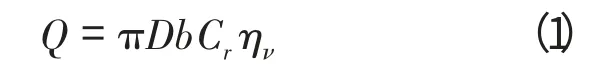
其中,
D为叶轮外径;
b为叶轮出口宽度;
Cr为径向分速度;
ην为离心泵的容积效率。
又由几何关系可以推出
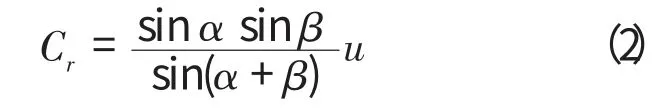
其中,
u为叶轮外缘线速度,且u=(πDn)/60;
n为叶轮转速。
由此可知,Cr是一个与转速有关的物理量。在转速一定的情况下,影响离心泵流量的主要因素是离心泵的容积效率。容积效率取决于容积损失,而容积损失是由于运动部件与固定部件之间的间隙而导致的在泵内由高压部位(出口)向低压部位(入口)的漏泄。叶轮间隙是容积损失发生的主要部位。间隙常常由初始条件及运行过程中的磨损所决定。
离心泵的容积效率可以表示为
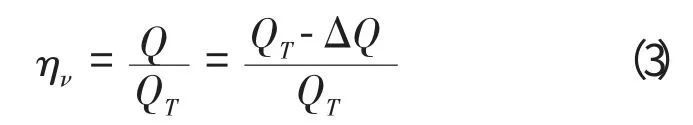
其中,
QT为水泵的理论流量,ΔQ为泄露损失流量。
这里主要考虑叶轮密封环的泄漏量,叶轮密封环泄漏量为
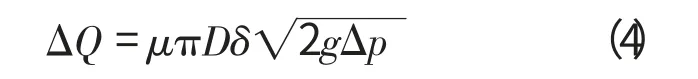
其中,
μ为流量系数,
δ为径向的密封环间隙,
g为重力加速度,
Δp为间隙两端压力降。

由式(1)、式(3)和式(5),可得到流量与间隙的物理关系式为

由式(6)可得
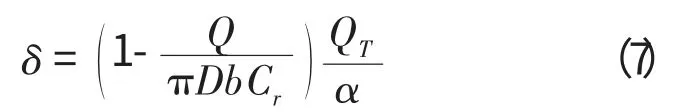
为保证离心泵不发生气蚀,泵的流量必须大于气蚀点所对应的最小流量Qmin。将最小流量代入式(7),可得间隙的极限允许值δmax。
当δ=δmax时,水泵就达到了极限状态。而这段过程所经历的时间,就是离心泵故障前使用时间T。依据可靠度理论,离心泵无故障工作概率为[2]
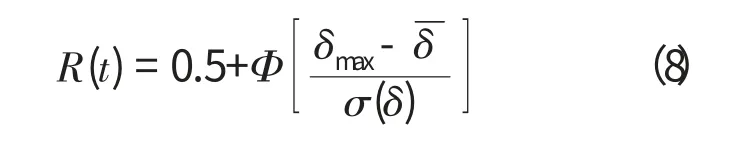
工程经验表明,进入正常磨损期的磨损项目,在磨损面上的正压力保持不变时,磨损量与工作时间之间的关系一般为线性。其他退化机理,例如冲蚀、腐蚀、表面结垢等,在退化机理的应力保持不变时,也大部分被认为是线性退化[3]。
本文中由磨损造成的间隙变化规律为

其中,
a为初始间隙;
γ为磨损速率;
t为产品的工作时间。
实际上,由于材料、工艺、装配等过程的不均匀性,初始间隙和磨损速率均是随机变量,工程上通常认为该随机变量服从正态分布。这时,使用时间是两个独立随机变量a 和γ的函数
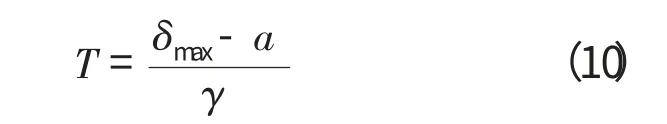
对于每一个t =T的值,参数δ 也服从正态分布,所以有
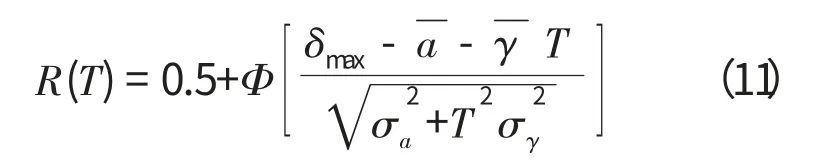
由式(11)就可以求出给定可靠度下的水泵寿命。
2 实例应用
某单级单吸离心泵,流量Q=2.79 m3/s,转速n=495 r/min,叶轮外径D=1 215 mm,叶轮出口宽度b=800 mm。
根据泵出厂时的最小流量Qmin=1.3 m3/s,可以求得δmax=4.24 mm。
通过对实际水泵的统计结果,可以得到水封环间隙与工作时间的关系。
本例中,初始间隙为服从
a~N(0.22,0.0152)的随机变量,磨损速率为服从
γ~N(0.000 220 6,0.000 0742)的随机变量。
由于T 2σy2的值比σa2的值小得多,故可取T 2σy2的值为零,可以得到
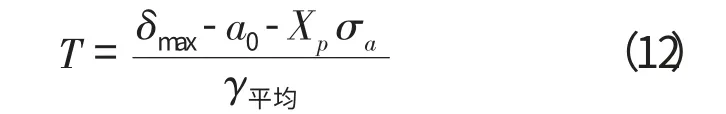
其中,Xp为给定概率下正态分布的分位数,计算结果如表1所示。

表1 水泵可靠度计算结果
从计算结果可以看出,应精确选择寿命,因为寿命时间的变化会显著影响无故障工作概率,而且产品还存在一个无故障工作概率接近于1的高可靠性区域。
3 结束语
本文模型是根据离心泵运行时可能的极限状态,并结合离心泵的初始运行条件,对离心泵工作能力耗损的强度进行评价,并推导出相应可靠度下产品的寿命计算公式。由于离心泵运行状况较为复杂,易受环境、运行载荷及人为操作的影响,评估其故障前使用时间具有一定的难度。
本文仅从造成离心泵故障的原因之一——流量不足出发,通过理论分析,得出寿命与磨损量之间的关系,从而简化了寿命评估的程序,具有一定的实际意义,且对离心泵的使用、维护和保养具有一定的指导作用。如果能考虑其他因素的影响,会进一步提高模型的准确性。
[1]姚寿广.船舶辅机[M].哈尔滨:哈尔滨工程大学出版社,2004.
[2]四川省机械工程学会设备维修专业委员会.机器可靠性[M].成都:四川人民出版社,1983.
[3]康 锐,李瑞莹.可靠性与维修性概论[M].北京:清华大学出版社,2004.
