蛋白质结构类预测方法研究
2012-12-19渤海大学数理学院数学系
渤海大学 数理学院 数学系 王 宇
蛋白质结构类的概念最初是由Levitt 和Chothia 在1976年提出的,他们根据蛋白质序列中二级结构片段的排列和拓扑结构的不同,将蛋白质序列分为4 个主要的类:一是all-α类,序列中主要包含α螺旋;二是all-β类,序列中主要包含β折叠;三是α/β类,序列中α螺旋和β折叠交替出现,而且β折叠是平行结构;四是α+β类,序列中α螺旋和β折叠被大距离地分开,而且β折叠是反平行结构。自此以后,蛋白质结构类预测得到了广泛发展。
目前,多数预测方式是基于蛋白质的一级结构序列——氨基酸序列来进行预测,主要是用氨基酸组成来表示蛋白质序列,无法反映蛋白质的其他信息。本文,笔者提出了一种新的基于氨基酸的12 种重要的物理化学性质和氨基酸的17 种分类的蛋白质序列表示方法,以及氨基酸在蛋白质序列中出现的位置来构造特征向量,然后利用贝叶斯决策作为分类工具,对同源性不超过25%的包含640 个蛋白质的数据集进行结构类型预测。
基于氨基酸在蛋白质序列中出现的位置和氨基酸的12 种重要的物理化学性质,以及氨基酸的17 种分类,构造出77-D特征向量来表示蛋白质序列,然后借助于贝叶斯决策对于同源性不超过25%的数据集进行蛋白质结构类型的预测研究,正确率达到 81.24%。
一、蛋白质的向量表示
1.提取氨基酸位置记数矩阵的不变量。对于任一氨基酸序列,要在蛋白质序列中考察某个氨基酸,当遇到该氨基酸时就需要对其在蛋白质序列中出现的位置进行计数,从而得到一个计数序列。对于某氨基酸序列:GKGDPKKPRGKMSSYAFFVQTSREEHKKKH,以K 为例,位置计数序列pk=(2,6,7,11,27,28,29)。对于蛋白质序列中每一个氨基酸都这样操作,从而一个蛋白质序列本质上就可以对应19 个计数序列。对每个氨基酸的计数序列,建立一个矩阵,其元素aij=|pjpi|。这样得到的矩阵是一个实对称的矩阵,通常称为线性矩阵。这样得到的19 个矩阵能反映序列中氨基酸前后的相关性。有了矩阵,就可以从中提取不变量,这里选用矩阵的最大特征值作为序列不变量。相应于19 个的最大特征值就可以构造一个19 维的向量。该氨基酸序列中,字母K 的线性矩阵见表1。
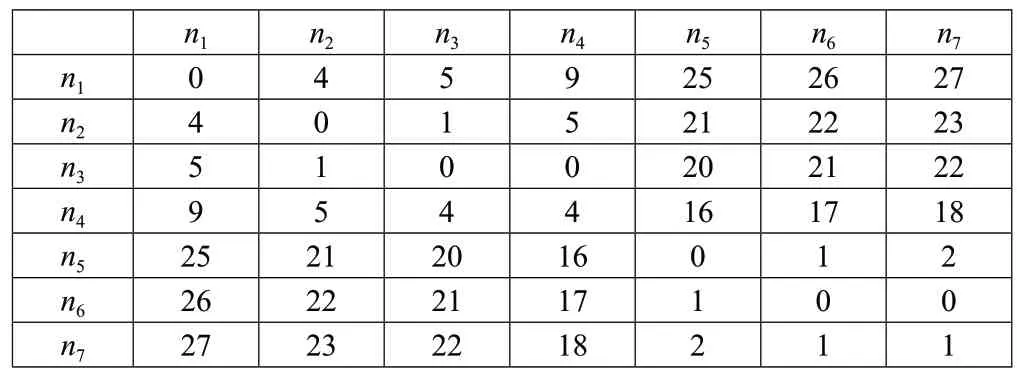
表1 字母K 的线性矩阵
2.基于氨基酸的12 种重要性质的(0.1)序列构造的向量。氨基酸是蛋白质的基本组成单位,其自身的特性必然会对蛋白质产生重要的影响。表2给出了20 种氨基酸的12 种重要性质。

表2 20 种氨基酸的12 种重要性质
对于一条长为n的蛋白质序列S=x1,x2,…,xn,根据氨基酸间的先后位置和以上12 种性质可以定义12 个映射(φ1,…,φ12),得到12 条(0,1)序列 (l1,l2,…,l12),构造如下映射。
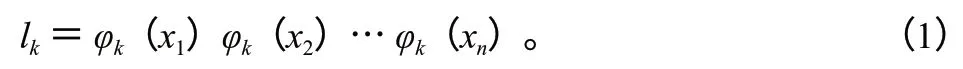
式(1)中,若Sk(xi)>Sk(xi+1),φk(xi)=0;反之,φk(xi)=1。特别的,当i=n时,φ(xn)=1;Sk为第K种性质(k=1,2,…,12),xi为蛋白质序列中的氨基酸。对于每条(0,1)序列,计算其LZ 复杂度及反LZ 复杂度,这样每条氨基酸序列就会有24 个特征向量。
3.基于17 个不同分类模型构造的向量。后34 维是基于20种氨基酸的17 个不同分类模型,结合生物信息学中LZ 复杂度和相对熵的相关理论构造而成的34 维特征向量V,表示如下。
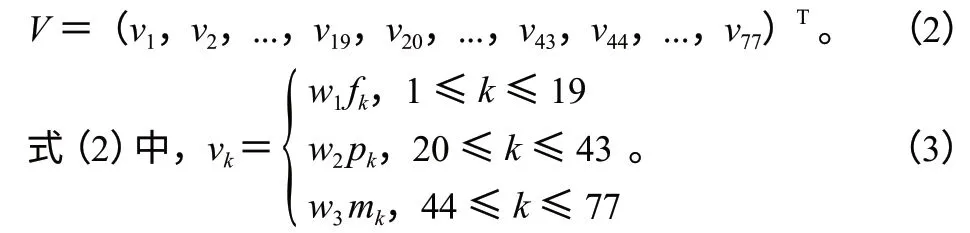
式(3)中,fk(k=1,2,…,19)表示位置矩阵的最大特征值,pk(k=20,21…,43)表示蛋白质序列转化成(0,1)序列的LZ 复杂度和反LZ 复杂度,mk(k=44,45,…,47)表示由17 种分类得出的34-D 向量,w1,w2和w3为权重系数。依据上述方法可将这640 条长度不同的氨基酸序列转化成640 个34-D 向量。
二、方法和数据
贝叶斯统计理论是贝叶斯在1763年创立的,是将归纳推论法用于概率论基础理论实现的。贝叶斯统计理论方法是统计模型决策中的一个基本方法,其基本思想为:根据已知类条件概率密度参数表达式和先验概率,利用贝叶斯公式转换成后验概率,根据后验概率大小进行决策分类。
据此,对于给定的一个未知类别样本,可先计算出其属于每类的概率,然后选择概率中最大的那个值所对应的类别作为这个未知类别样本的类别。对all-α类的138 个向量、all-β的154 个向量、α/β的177 个向量、α+β的171 个向量分别平均分成5 份,然后依次以这5 份中的一份作为测试集,其余作为训练集。这样分5 次算出预测的结果,然后再取平均值,这个平均值作为这次的最后结果。基于上述的分类方法,随机做20次试验,试验的准确度见表3。同时,将该方法与其他其他方法进行了比较,比较结果见表4。

表3 随机20 次试验的准确度

表4 多种方法预测准确度的比较
对于方法2,3,4,在all-α类上差距比较大;在all-β类上的精度比方法2,3,4 高出很多;在α/β类上与方法(2)比较接近,与方法3,4 分别相差2.63%,3.74%;在α+β类精度上比法2,3,4 分别高出8.62%,3.92%,1.05%。在总精度上我们比法2 高出0.44%,与法2,3 相差1.86%,2.20%。与方法5,6,7,8,9,10,11 相比,除了方法比9,11 的all-α类上略低了一点,其余无论是在总精度,还是在各个分类的精度都有较大挺高。
