中国月度婴儿出生率预测

河南大学 数学与信息科学学院 王文静

针对中国现阶段老龄化趋势不断增加，笔者认为，有必要分析一下中国目前婴儿出生率的状况，选择了《应用时间序列分析》课本上的某城市月度婴儿出生率数据，经过用软件对这些数据分析发现，分析结果符合中国现在的情况，即我国从过去的实行计划生育政策鼓励一个家庭要一个孩子，到现在的准许部分家庭要两个孩子，从政策的放宽可以发现我国的月度婴儿出生率在不断地增加。根据这些数据对中国月度婴儿出生率确定一个模型，可以预测未来中国婴儿的出生情况。运用时间序列知识来解决实际中的问题，从某城市月度婴儿出生率数据找出其规律，来推测未来月度婴儿出生率的问题。

一、绘制序列时序

图1为某城市月度婴儿出生率序列时序。

图1 某城市月度婴儿出生率序列时序

时序图显示该序列具有长期递增趋势和一年为周期的季节效应。根据时间序列的处理方法，要对其数据进行平稳性处理，因此下面一步要进行差分平稳化处理。

二、差分平稳化

对原序列作阶步差分，希望提取原序列趋势效应和季节效应，差分后序列时序如图2所示。

图2 某城市月度婴儿出生率阶步差分后序列时序

该时序图显示差分后序列类似平稳。下面就要根据时间序列的相关知识进行模型定阶。

三、模型定阶

考察差分后序列自相关图的性质，进一步确定平稳性判断，并估计拟合模型的阶数，如图3所示。

图3 某城市月度婴儿出生率阶步差分后序列自相关情况

自相关图显示延迟步自相关系数显著大于倍标准差范围，这说明差分后序列中仍蕴含着非常显著的季节效应。延迟步的自相关系数也大于倍标准差，这说明差分后序列还具有短期相关性。这时，通常假定短期相关性和季节效应之间具有乘积关系，尝试使用乘积拟和序列的发展。乘积模型的构造原理如下：

当序列具有短期相关性时，通常可以使用低阶ARMA（P，Q）模型提取。

当序列具有季节效应，季节效应本身还具有相关性时，季节相关性可以使用以周期步长为单位的ARMA（P，Q）模型提取。

由于短期相关性和季节效应之间具有乘积关系，所以拟合模型实质为ARMA（P，Q）和ARMA（P，Q）的乘积。综合前面的d阶趋势差分和D阶以周期S为步长的季节差分运算，对原观察值序列拟合的乘积模型完整的结构如下：

考虑到差分后序列短期相关性显著，尝试拟合乘积模ARMA（0，1，3）×（0，1，1）12，

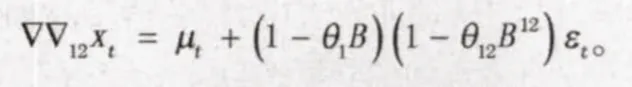
下面，运用SAS程序进行参数的估计。

四、参数估计

使用条件最小二乘估计方法，确定该拟合模型的口径为：

该模型适用显著性水平大于0.1 的情况。下面对模型的准确性进行检验。

五、模型检验

对拟和模型进行检验，检验结果显示该模型顺利通过残差白噪声检验和参数显著性检验。

将序列拟合值和序列观察值联合作图，可以直观地看出该乘积模型对原序列的拟合效果良好，如图4所示。

图4 某城市月度婴儿出生率序列拟合效果

图4中，点为序列观察值；曲线为序列拟合值。在模型合适的情况下进行预测，观察预测图是否合适。

六、预测

从上面的分析结果可以知道，根据某城市月度婴儿出生率的数据的得到婴儿出生率的预测模型是合理的。故月度婴儿出生率的预测模型为：

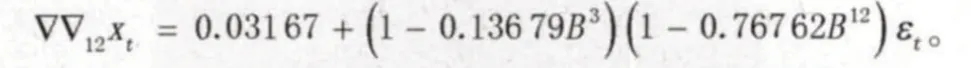
模型适用显著性水平大于0.1的情况。