双层黏弹介质模型条件下地震应力扰动的时空特征

蒋海昆，吴 琼，宋 金，李 金，曲均浩

1 中国地震台网中心，北京 100045

2 中国地震局地震预测研究所，北京 100036

3 中国地震局地质研究所，北京 100029

双层黏弹介质模型条件下地震应力扰动的时空特征

蒋海昆1，吴 琼1，宋 金1，李 金2，曲均浩3

1 中国地震台网中心，北京 100045

2 中国地震局地震预测研究所，北京 100036

3 中国地震局地质研究所，北京 100029

基于简化双层黏弹介质模型及其变形过程的时间属性，考虑震后地壳上层（黏滞性相对较弱）短时间的弹性扰动及后续较长时间内下层（黏滞性相对较强）黏性变形对上层应力扰动的联合作用，研究地震应力扰动的时空变化.结果显示，地震应力扰动在震后一段时间内逐渐增大，之后缓慢衰减.并且模型参数越接近真实地体，应力扰动增大及衰减过程就越缓慢，持续时间越长，即地震活动具有较长时期的时间“记忆”特性.因而，在地震活动及库仑应力变化研究中，长时期的应力扰动影响不宜忽略.地震应力扰动有一定的空间作用范围，在此范围内应力扰动随距离衰减明显，距离震源较近处衰减较快、距离震源较远处衰减相对较慢，此范围之外应力扰动可忽略不计.在本文所取与实际地壳相对较为接近的模型参数条件下，应力扰动的空间作用范围大体是震源线性破裂尺度的2.5倍.地震应力扰动随震级增大而逐渐增大，在本文模型参数条件下，震级大于6级之后，应力扰动随震级快速增加.地震破裂尺度测量误差所导致的应力扰动计算误差的相对大小，与时间无关，与破裂尺度（震级）及震源距有关，随震源距的增大而增大，但对应力扰动的总体变化趋势及变化范围影响甚微.当距离足够远时，应力扰动计算误差的相对大小趋于常数，就6、7、8级地震而言，最大应力扰动计算误差分别小于应力扰动值本身的22%、30%及38%.

双层黏弹介质地壳模型，地震应力扰动，持续时间，作用范围，主震震级

1 引 言

一次地震发生后，地震断层永久位移产生的小的“静态”应力变化，可以改变附近断层上发生地震的可能性，或者说可能触发地震［1］.许多近场的触发地震、特别是触发余震的研究，将这种静态应力变化视为触发因素，并认为其与断层上的负载变化等价［2－3］.已有研究表明，大多数余震发生在库仑破裂应力增加的区域［1］，地震活动率在库仑破裂应力增加的区域增大、在库仑破裂应力减小的区域降低［4］，即大地震导致的区域应力变化是区域地震活动增强的原因.例如，1992年Landers7.3级地震后，余震分布在库仑破裂应力增加大于0.03MPa的区域［4］，震后在距离Landers地震主断层5～75km的范围内，85%的余震事件与静应力增加相一致［5］.事实上，关于断裂之间相互作用、以及与地震活动之间的关系，早在1960～1980年代即已进行过深入的探讨［6－14］，当时已知一次较强地震的位错在周围区域产生的静态库仑应力变化一般是10－2～10－1MPa量级，但认为这很难导致或触发另一次地震的发生，因为根据岩石摩擦实验结果，地壳中、上部最大摩擦强度可能是几千兆帕［15］.但1980年代以来，随着非线性动力学的发展，认为地球动力系统处于自组织临界状态［16］，而临界状态下微小的应力扰动即可触发地震活动.

存在的问题是，具有有效触发影响的库仑应力变化量值及影响范围究竟如何？关于前者，全球研究结果的综述表明［17］，库仑破裂应力变化大于10－1～10－2MPa即有可能触发余震或后继地震，这一应力变化量值，比月相潮汐应力（约10－3MPa）大约101～102倍.关于后者，检测应力扰动有效范围的最理想方法，是在足够大的区域开展应力的直接测量，但这实际上无法实现.理论上，一般认为应力场空间结构的时间演化，是由相对稳定的远场背景应力与局部应力扰动的叠加，同时耦合有非常复杂的地壳流变响应.为合理估计应力扰动及其随时间的演变，需要局部岩石圈的精确流变学模型，包括黏滞层弹性常数及松弛时间等数据，这些数据在大尺度上可由地球物理学调查、推论得到，但由于结构的复杂性，确定精确的模型参数仍存在诸多困难［18］.幸运的是，依据临界点理论，只要背景应力变化在时间尺度上足够缓慢，应力扰动即可视为仅与地震发生有关，而不属于大尺度边界力学条件产生的影响.因而，针对不长的研究时间段内（数月至数十年）的地震活动过程，可以暂不考虑应力场远场边界条件的影响.根据这一特点，为研究有限时空尺度内应力场的波动问题，Ouillon等提出一种简化的地壳流变学模型［19］，它突出了黏弹性分层介质内部应力传播和松弛这一本质特征，而对其他可能的影响因素则进行了简化.事实上，我国20世纪八、九十年代在大陆构造应力场和应变传播的数值模拟研究中，也已开始引入弹塑性或黏弹性理论［20－21］，从地幔及下地壳塑性流动特性出发，对壳幔力学行为、大尺度塑性流动网络构造及其应力、应变特性等开展了许多理论、物理模拟及数值模拟实验研究［22－24］，近期部分关于库仑应力触发的研究也开始引入黏弹性质［25－28］.

本文将基于文献［19］模型，考虑双层黏弹介质及其变形过程的时间属性，假定地震对某处的应力扰动包含短时间的弹性扰动及较长时间的黏性变形扰动两部分，在简化模型的前提下，讨论地震应力扰动的时、空变化及与主震破裂尺度的关系等问题.

2 双层黏弹介质模型中地震导致的应力扰动

Ouillon等［19］给出双层黏弹介质模型中标量格林函数形式的应力扰动表达式.

假定震源辐射各向同性，且围绕震源呈半径对称分布，则均匀弹性介质中点源产生的应力扰动（stress perturbation）随震源距r衰减［19］：

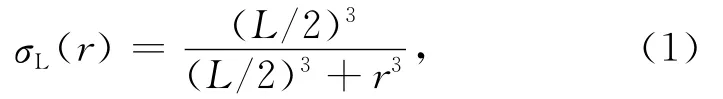
L为震源线性尺度.由于柱对称的应力扰动σL（r）始终为正，因而σL（r）不是真实的应力，但可理解为一种影响函数，表征一次地震事件对应力场的可能影响，影响范围由L控制.

进一步考虑最简单的双层黏弹介质模型，下层为半无限空间，上、下层黏弹介质松弛时间分别为τ1、τ2，τ1＞τ2.松弛时间的物理含义是，由于模型中黏性元件的黏滞作用，延缓了弹性元件的应力松弛或应变恢复，在应力松弛或应变恢复过程中，当应力或应变降低到初始值的1／e时所经历的时间称为松弛时间.因而从力学作用方式及应变松弛过程来看，该模型上、下层可简单理解成剪切模量和剪切黏度不同的Maxwell体，上层还串联有滑块以模拟突然滑动的地震过程，模型上、下两臂之间并行联结（图1）.

图1 简化的双层黏弹介质模型示意图Fig.1 Sketch map of the simplified two－layer viscoelastic medium model

假定地震发生在相对脆性的上层，地震导致的应力场瞬间的弹性解由式（1）给出.地震瞬间的弹性变形在上层产生一个直接的弹性应力加载，由于上层的黏弹性质，之后将在上层导致弹性应力松弛.与此同时，地震时介质瞬间弹性变形所导致的应力传递，亦将激发对下层的应力加载，同样导致下层介质的黏滞松弛过程.由于下层黏滞性强于上层，其介质流动较上层更为容易，因而下层的黏滞松弛过程反过来对上层产生延迟加载，下层黏滞松弛过程对上层的加载影响表达为［19］

此处σL（r）是由式（1）给出的弹性各向同性解，C是表征上层应力迁移最大量值的常数，与模型几何结构有关，若C＝0则没有应力转移.H（t）为Heaviside函数，其作用是确保一旦地震发生，其应力波动不为零.t是自地震之后的流逝时间.这一时期，上层应力也按exp（－t／τ1）方式松弛.当上、下两层黏弹介质松弛过程同时发生时，则上层总的应力扰动来源于两部分的贡献：其一是地震在上层产生瞬间弹性应力加载之后所导致的应力松弛σL（r）exp（－t／τ1），其二是地震后下层黏滞松弛在上层所导致的应力加载f（r，t）时间导数的卷积，f（r，t）具有指数形式exp（－t／τ1）的松弛特征.第二部分贡献汇聚了由于下层松弛而在上层每单位时间所导致的应力源增加df（r，t）／dt.经过一定的数学处理之后，由于地震所导致的、总的应力扰动为［19］

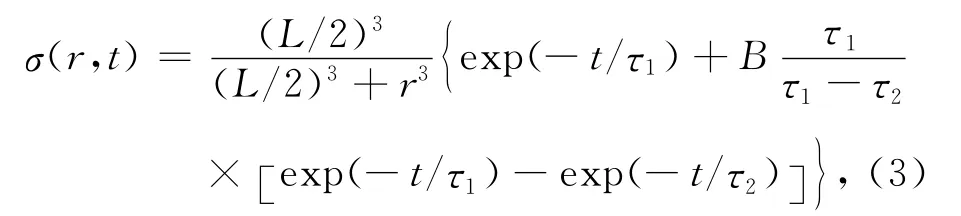
r和t分别是震源距和地震之后的流逝时间.参数B是表征下层松弛对上层应力延迟加载作用强弱的常数，B强烈依赖于双层黏弹介质模型各层的几何及流变性质，其真实数值难以确定.B＝1意味着上、下两层介质震后松弛过程所导致的应力扰动贡献，与震级具有相同的量级；B＝0则表明仅考虑上层松弛过程而忽略下层的影响.如果研究点附近区域起算震级以上地震之间的平均时间间隔大于下层松弛时间τ2，则这种忽略对最终结果的影响非常小［19］.由于本文力图研究双层黏弹介质模型条件下的地震应力扰动，因而取B＝1.

式（1）及式（3）中的震源线性尺度L与地震破裂尺度或余震分布尺度相当.本文使用依据中国大陆143次主余型序列得到的统计关系［29］，经由震级M计算得到：

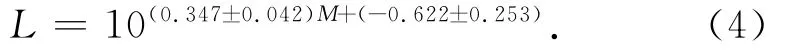
3 结果及讨论

在实际地壳介质状况下，上地壳松弛时间τ1介于数千至数十万年之间，下地壳松弛时间τ2介于数年至数百年之间，主要与剪切模量G及剪切黏度η有关（表1）［22］.为从概念上探讨简化双层黏弹介质模型条件下，上、下层介质黏滞性质对地震应力扰动的影响，以下选择三种τ1、τ2组合进行讨论（单位为“月”），分别是：（1）τ1＝1200、τ2＝120；（2）τ1＝120、τ2＝12；（3）τ1＝12、τ2＝4.三种情形地壳上、下层的流变性均大大高于实际，其中第一种情况在量级上与实际相对接近.

已有研究表明，地震库仑破裂应力变化大于10－1～10－2MPa即有可能触发地震［17］.一般而言，小震应力降可粗略地视为常数［30］，但对破裂尺度明显大于震源深度的大地震，在记录频段确定的情况下，应力降与震级、震源深度定性正相关［31－33］，与破裂类型也有一定关系［34］.总体而言，不同区域、不同时段、不同震级范围地震应力降分布于10－2～102MPa，绝大多数介于100～101MPa之间（中位值）.例如，利用地下2.5km深井地震仪记录的圣安德列斯断层附近100多次ML1.0～5.0级地震资料计算的应力降中位值约为3MPa［35］，旧金山湾1998—2007年间529次M1.0～4.2级地震的应力降中位值约为8.7MPa［33］；1900—1998年全球7400余次MS4.0～8.2级地震应力降中位值约为2.3MPa［36］，等等.由于震时（t＝0）震源地方（r＝0）的应力扰动与地震应力降相当，因而10－1～10－2MPa这一能够触发地震活动的库仑应力变化量值，粗略地相当于大多数地震应力降的10－1～10－2倍.另一方面，τ1＝1200、τ2＝120条件下，由无量纲标量函数式（3）得到的震时震源地方的应力扰动等于1（参见图2a线（1）及图3a中最下边一条曲线所示），对比上述库仑应力变化触发地震的研究结果，为方便问题讨论，本文简单地取0.01为应力扰动的“有效”值，0.01大体相当于τ1＝1200、τ2＝120条件下震时震源地方应力扰动的10－2倍.

表1 地壳介质的松弛时间［22］Table 1 The relaxation time of crust medium［22］

3.1 地震应力扰动随时间的变化

图2 不同距离地震应力扰动随时间的变化（a）r＝0；（b）r＝50km；（c）r＝100km.（1）τ1＝1200、τ2＝120；（2）τ1＝120、τ2＝12；（3）τ1＝12、τ2＝4；τ1、τ2单位为“月”；M＝7.0.Fig.2 Variation of earthquake stress perturbation with the distance

为简化讨论，统一取式（4）中主震震级M＝7.0.图2给出不同区域地震应力扰动随时间的变化，可见对与实际较为接近的τ1、τ2组合（τ1＝1200、τ2＝120），震源地方（r＝0）应力扰动在震后随时间缓慢增加，这一过程大体上可持续20年（约220个月），之后缓慢减小，减小过程亦可持续数十年（图2a线（1））；若增大双层黏弹介质的黏滞性质，取τ1＝120及τ2＝12（图2a线（2）），则震后不长的时间内（约22个月），震源地方应力扰动增强明显，之后随时间持续减小，减小速率亦逐渐变小，50多年后（约643个月）应力扰动小于0.01；进一步增大双层黏弹介质的黏滞性质，取τ1＝12及τ2＝4（图2a线（3），这是一种远离实际的情形），这种条件下，震后极短的时间内（约4个月），震源地方应力扰动快速增长，之后随时间快速降低，大约5.5年（约66个月）后应力扰动已趋于0（＜0.01）.

r＝50km及r＝100km处应力扰动随时间的变化分别如图2b及图2c所示，图中曲线（1）、（2）、（3）含义与图2a相同，可见不同τ1、τ2组合条件下应力扰动随时间的变化趋势与图2a类似，应力扰动最强的时间T1也与图2a震源地方的相同，但应力扰动强度有显著差异（图2，表2）.对相同的震源距r，双层黏弹介质模型黏滞性越强，应力扰动衰减到小于0.01所需的时间T2越短.例如就震源地方（r＝0）而言，对与实际较为接近的τ1、τ2组合（τ1＝1200、τ2＝120），应力扰动随时间衰减缓慢，T2远大于本文的最大模拟时间（60年）；增大双层黏弹介质模型的黏滞性质，当τ1＝120、τ2＝12时，T2≈54年；继续增大模型的黏滞性，取τ1＝12、τ2＝4，则T2≈5.6年.对相同的双层黏弹介质模型（相同τ1、τ2组合），应力扰动衰减到小于0.01的时间T2随震源距r的增大而减小，例如对τ1＝120、τ2＝12的模型参数组合，r＝0、50及100km所对应的T2分别约为54、38及19年（表2第5列）.

表2 不同模型参数及震源距条件下应力扰动最强的时间（T1）及应力扰动趋于0的时间（T2）Table 2 The time of maximum stress perturbation and the time of stress perturbation tends to 0，with different model parameters and in different distance

3.2 地震应力扰动随空间距离的衰减

取双层黏弹介质模型上、下两层松弛时间τ1＝1200月、τ2＝120月.假定地震在上层发生，分别选取t＝0、t＝6月、t＝12月及t＝24月等四个震后时间点，研究震后不同时刻地震应力扰动随震源距r的变化，结果如图3所示，图3a、3b分别为震级M＝7.0和M＝6.0时的结果.在所选定的黏弹介质模型条件下（τ1＝1200、τ2＝120），当主震震级M＝7.0时（图3a），50km范围内应力扰动随距离衰减较快，之后逐渐变缓，大约150km范围之外，应力扰动趋于0（＜0.01）；降低主震震级至M＝6.0（图3b），30km范围内应力扰动随距离衰减较快，之后逐渐变缓，大约60～70km范围之外，应力扰动趋于0（＜0.01）.简言之，①震后同一时刻应力扰动随震源距r的增加而快速减小；②较大地震应力扰动的有效作用距离相对较大；③同一地方应力扰动随时间增加而略有增大，震源距r越小的地方增加越明显.

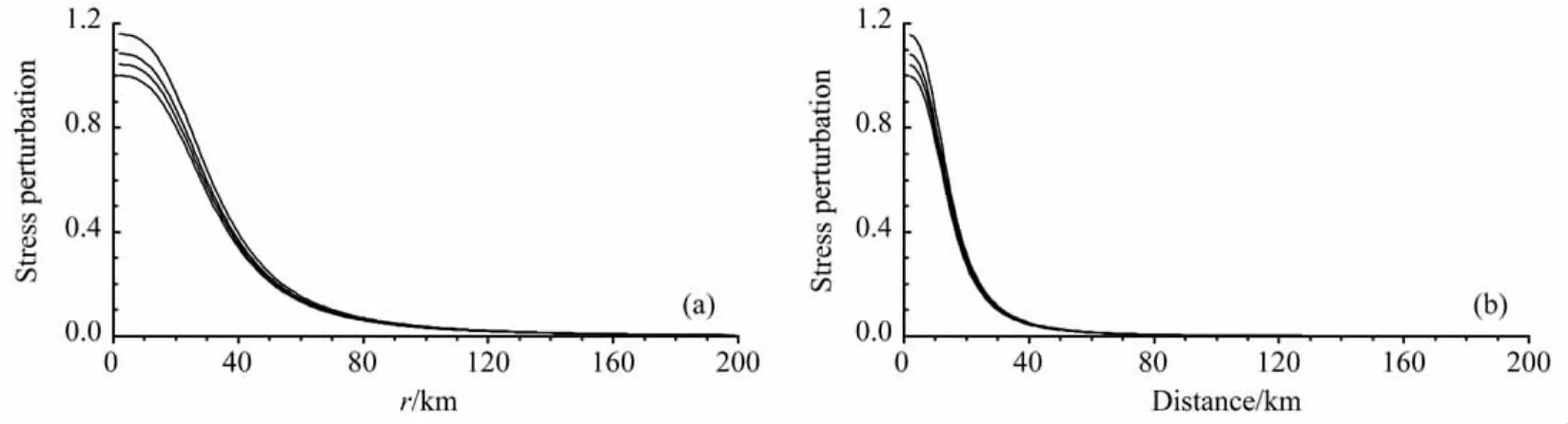
图3 不同时刻地震应力扰动随距离的变化（τ1＝1200、τ2＝120；τ1、τ2单位为“月”）（a）M0＝7.0，曲线从上到下依次对应t＝24、t＝12、t＝6及t＝0的结果（t单位为“月”）；（b）M0＝6.0，曲线从上到下依次对应t＝24、t＝12、t＝6及t＝0的结果（t单位为“月”）.Fig.3 Variation of stress perturbation with distance in different time（τ1＝1200，τ2＝120；The unit ofτ1andτ2is month）

3.3 地震强度对应力扰动的影响

参考上述关于应力扰动随时间和距离变化的研究结果，取双层黏弹介质模型上、下两层松弛时间τ1＝1200、τ2＝120（单位为“月”），考察震后220个月时（t＝220）空间上不同距离处应力扰动随震级的变化，220个月大体上相当于τ1＝1200、τ2＝120条件下应力扰动达到最大的时间（参见图2及表2），结果如图4所示.可见震源地方（r＝0，线（1））应力扰动不随地震震级大小而变化，这从式（3）亦可看出，时间t确定之后，应力扰动决定于线性震源尺度L（L∝10M，M为地震震级）及震源距r，r＝0时应力扰动为常数，这与常应力降模型或不同震级地震应力降差异不大这一观测事实定性一致［37－38］.对远离震源地方的区域（r＞0），应力扰动（线（2）、（3）、（4））总体上随震级增大而增大，与破裂尺度随震级的变化趋势（空心圆）大体类似.对相同大小的地震，距离越近（r越小）应力扰动越大、距离越远（r越大）应力扰动越小；对距离固定的区域，较低震级地震（例如M＜6）应力扰动非常弱，震级大于6级之后，应力扰动随震级快速增加，但当震级非常大的时候（例如M＞8），应力扰动随震级的增幅逐渐变缓.具体来看，对τ1＝1200、τ2＝120的模型参数，震后220个月的时候，震源距r分别为50、100及200km的地方，所导致应力扰动大于0.01的地震震级分别应大于5.5、6.4和7.2级.由式（4）可知，上述三个震级对应的线性震源尺度大约分别为19、43及88km，因而50、100及200km距离分别约为上述破裂尺度的2.5～2.6倍.为对比，取t＝20进行类似计算，所得上述比例大约介于2.2～2.4之间，而τ1＝1200、τ2＝120这一模型参数条件下，地震应力扰动在t＝20时并未达到最大.换言之，在所取与实际较为接近的双层黏弹模型参数条件下，最大的有效应力扰动范围约为震源线性破裂尺度的2.5倍，对更远地方的应力扰动可忽略不计.

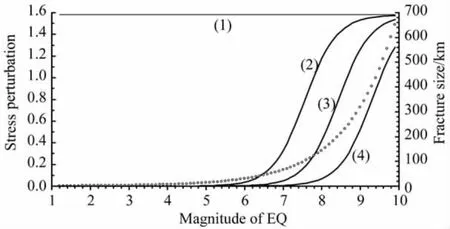
图4 不同距离处应力扰动（左，震后220个月的结果）、破裂尺度（右，空心圆）随震级的变化τ1＝1200、τ2＝120，t＝220.（1）r＝0；（2）r＝50km；（3）r＝100km；（4）r＝200km.Fig.4 Variation of stress perturbation（left，the results of 220months since the mainshock）and fracture size（right，empty circle）with the magnitude

3.4 地震破裂尺度测量误差对应力扰动的影响

除少数大地震震后有较为深入的野外考察外，地震破裂尺度大多依据余震分布范围或依据统计关系粗略得到.由于震级测量及余震定位等因素的不精确性，以往地震破裂尺度与主震震级的统计关系（4）式存在较大的离散（参见文献［29］），由此导致破裂尺度测量存在误差，近似条件下，这种误差或离散体现在（4）式回归参数的变化上.

为讨论破裂尺度测量误差对应力扰动计算的影响，将（4）式写为

分别求L对a、b的偏导数：

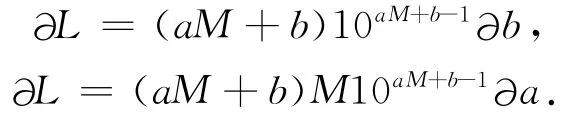
两式相加有：

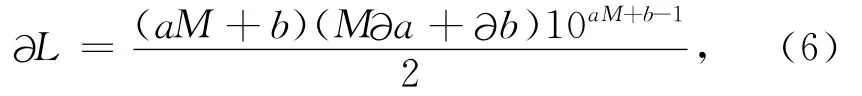
（6）式中∂L可理解为由于回归系数a、b的误差∂a、∂b所导致的L的误差.

利用式（3）求σ（r，t）对L的偏导数：

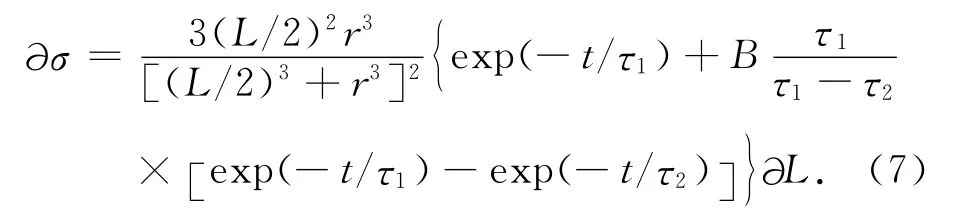
∂σ是由于L的测量误差∂L所导致的σ的计算误差.考虑∂σ对σ的相对变化，并将（5）、（6）式代入（7）式有

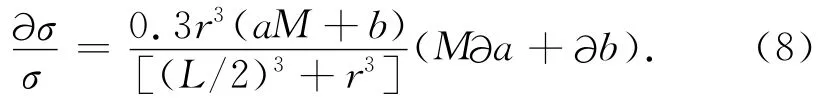
（8）式给出由于破裂尺度测量误差（以∂a、∂b表达）所导致应力扰动计算误差的相对大小（∂σ／σ），可见（∂σ／σ）与时间无关，与破裂尺度L（主震震级）及震源距r有关.若震源距r足够大，则（∂σ／σ）→0.3（aM＋b）（M∂a＋∂b），此即应力扰动计算误差的极限.

将（4）式中有关参数a＝0.347、∂a＝0.042，b＝－0.622、∂b＝0.253代入（8）式，并设定其中M＝7.0，数值计算结果显示，应力扰动计算误差的相对大小（∂σ／σ）随震源距r的增大而增加，r小于30km时，应力扰动的计算误差小于应力扰动值的10%，r小于40km时小于20%，r小于200km时小于30%.关于应力扰动计算误差相对大小的极限值，对6、7、8级地震而言，r→∞＋时，（∂σ／σ）分别趋于0.221、0.297及0.381.

取M＝7.0、t＝0、以及τ1＝1200、τ2＝120，图5给出图3a中最下面一条曲线的结果，其中误差棒表示由于破裂尺度的测量误差所导致的应力扰动计算误差∂σ，可见对应力扰动的总体变化趋势并无影响.并且，尽管应力扰动计算误差的相对大小（∂σ／σ）随震源距r的增大而增加，但由于应力扰动本身随震源距快速衰减，因而绝对误差∂σ并不随距离增大而无限制地增大.

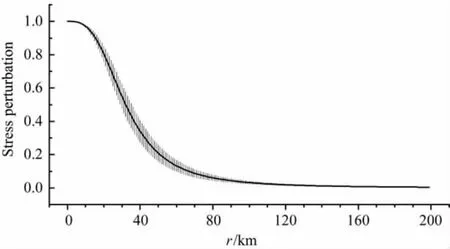
图5 t＝0时刻地震应力扰动随距离的变化（τ1＝1200、τ2＝120；τ1、τ2单位为“月”）误差棒表示由于破裂尺度的测量误差所导致的应力扰动计算误差.Fig.5 Variation of stress perturbation with the distance at the time of t＝0（τ1＝1200，τ2＝120；The unit ofτ1andτ2is month）

4 结 论

引入简化的双层黏弹介质模型及其变形过程的时间属性，考虑震后应力扰动为短时弹性应力扰动及后续较长时间下层黏性变形对脆性层（上层）应力扰动的累积，研究地震应力扰动的时空变化.主要结论如下：

（1）地震应力扰动在震后不长的时间内逐渐增大，之后缓慢衰减，并且双层黏弹介质模型上、下层松弛时间越接近真实地体，地震应力扰动逐渐增大及之后的缓慢衰减过程就越缓慢，作用持续时间越长.这意味着，地震活动具有较长时期的时间“记忆”特性.这与Ouillon等提出的多分形应力激活模型（multifractal stress activation model）［39］相吻合，这一模型有两点重要预期，一是引发地震破裂的激活过程与当地应力的指数增长有关，二是应力扰动具有长效记忆性.

（2）地震应力扰动随地震震级增大而逐渐增大，在本文假定的与实际相对接近的模型参数条件下，震级大于6级之后，应力扰动随震级快速增加.

（3）地震应力扰动随距离衰减明显，距离较近处衰减较快、距离较远处衰减相对较慢.地震应力扰动有一定的空间作用范围，粗略来看，在本文所取与实际地壳较为接近的模型参数条件下，应力扰动的空间作用范围大体上是震源线性破裂尺度的2.5倍，超过此范围的区域，应力扰动已经非常小（趋于0），可忽略不计.

需要指出的是，这一认识是基于点源模型、假定所有能量均在破裂起始点处释放得到的结果，其应力扰动有效的空间影响范围限于破裂尺度的数倍.对大地震而言，例如5·12汶川8.0级地震，其地表破裂尺度已近240km［40］，震源时间函数接近60s［41］，这时再把整个地震过程看作点源显然不当.一种变通的考虑是，可把破裂过程离散化，整个破裂过程作为一系列移动点源的积分，点源的强度参考震源时间函数确定.可以预见，如此处理所得到的应力扰动影响范围，在量级上与前述结果相比不会有明显的变化.上述结果及认识可得到实际观测结果的定性验证［42］.在2008年5月12日汶川Ms8.0级大震前一周，采用水压致裂技术在龙门山断裂带北段ZK1测点地下300～400m深度上测得的最大水平主应力值为21～22MPa，与其附近下盘ZK4测点最大水平主应力值之差高达8～10MPa；汶川地震后原地重复测量结果表明，发震断裂带上ZK1测点的最大、最小水平主应力值分别降低了29%和23%，而下盘ZK4测点的地应力状况并无变化，ZK1与ZK4测点之间距离不过40多公里.尽管地震应力扰动的作用时间不足够长，并且下盘ZK4测点不在破裂的传播方向上，但作为一次8级巨大地震，其应力扰动随距离的衰减可谓相当明显.

（4）由于震级测量及余震定位等因素的不精确性，破裂尺度的测量或计算存在误差，由此导致的应力扰动计算误差的相对大小与时间无关，与破裂尺度L（主震震级）及震源距r有关，随震源距r的增大而增加，但对应力扰动的总体变化趋势及变化范围影响非常小.当r趋于无穷时，应力扰动计算误差的相对大小趋于常数.就6、7、8级地震而言，应力扰动计算误差的最大值分别小于应力扰动值本身的22%、30%及38%.

（5）由于真实地体中地震产生的应力扰动衰减缓慢、持续时间长、显示较长时期的时间“记忆”特性，因而地震活动及库仑应力变化研究中，此前长时期的地震应力扰动影响不能忽略；由于地震产生的应力扰动随距离衰减明显，因而在开展静态库仑应力变化触发地震活动研究时，应重点关注震中附近区域，较远处则可能触发作用不再明显.由于震级不高时的应力扰动非常弱，因而通过库仑应力变化研究未来地震区及其地震危险性时，以研究强震的库仑应力变化为宜.

（References）

［1］ Harris R A.Introduction to special section：stress triggers，stress shadows，and implications for seismic hazard.J.Geophys.Res.，1998，103（B10）：24347－24358.

［2］ Toda S，Stein R S，Reasenberg P A，et al.Stress transferred by the 1995 Mw＝6.9Kobe，Japan，Shock：effect on aftershocks and future earthquake probabilities.J.Geophys.Res.，1998，103（B10）：24543－24565.

［3］ King G C P，Stein R S，Lin J.Static stress changes and the triggering of earthquakes.Bull.Seism.Soc.Am.，1994，84（3）：935－953.

［4］ Reasenberg P A，Simpson R W.Response of regional seismicity to the static stress change produced by the Loma Prieta earthquake.Science，1992，255（5052）：1687－1690.

［5］ Hardebeck J L，Nazareth J J，Hauksson E.The Static stress change triggering model：constraints from two southern California aftershock sequences.J.Geophys.Res.，1998，103（B10）：24427－24438.

［6］ Chinnery M A.The stress changes that accompany strike－slip faulting.Bull.Seism.Soc.Am.，1963，53（5）：921－932.

［7］ Smith S W，Van de Lindt W.Strain adjustments associated with earthquakes in southern California.Bull.Seism.Soc.Am.，1969，59（4）：1569－1589.

［8］ Rybichi K.Analysis of aftershocks on the basis of dislocation theory.Phys.Earth Planet Inter.，1973，7（4）：409－422.

［9］ 陈运泰，林邦慧，林中洋等.根据地面形变的观测研究1966年邢台地震的震源过程.地球物理学报，1975，18（3）：164－182.Chen Y T，Lin B H，Lin Z Y，et al.The focal mechanism of the 1966Hsingtai earthquake as inferred from the ground deformation observations.Chinese J.Geophys.（in Chinese），1975，18（3）：164－182.

［10］ Yamashina K.Induced earthquakes in the Izu Peninsula by the Izu－Hanto－Oki earthquake of 1974，Japan.Tectonophysics，1978，51（3－4）：139－154.

［11］ 黄福明，王廷韫.倾斜断层错动产生的应力场.地震学报，1980，2（1）：1－20.Huang F M，Wang T Y.The stress field of a dislocating inclined fault.Acta Seismologica Sinica（in Chinese），1980，2（1）：1－20.

［12］ 王仁，何国琦，殷有泉等.华北地区地震迁移规律的数学模拟.地震学报，1980，2（1）：32－42.Wang R，He G Q，Yin Y Q，et al.A mathematical simulation for the pattern of seismic transference in north China.Acta Seismologica Sinica（in Chinese），1980，2（1）：32－42.

［13］ 郭增建，秦保燕.大震重复性与减震作用.／／国家地震局科技司.近期强震危险性研究.北京：地震出版社，1989：455－456.Guo Z J，Qin B Y.Repeatability and weakening action of the large earthquakes.／／Department of Science ＆Technology，National Seismological Bureau.Study on the Recent Seismic Risk of Large Earthquakes（in Chinese）.Beijing：Seismological Press，1989：455－456.

［14］ Das S，Scholz C H.Off－fault aftershock clusters caused by shear stress increase？Bull.Seism.Soc.Am.，1981，71（1）：1669－1675.

［15］ Byerlee J D.Friction of rocks.PAGEOPH，1978，116（4－5）：615－626.

［16］ Bak P，Tang C.Earthquakes as a self－organized critical phenomena.J.Geophys.Res.，1989，94（B11）：15635－15638.

［17］ 万永革，吴忠良，周公威等.几次复杂地震中不同破裂事件之间的“应力触发”问题.地震学报，2000，22（6）：568－576.Wan Y G，Wu Z L，Zhou G W，et al.“Stress triggering”between different rupture events in several earthquakes.Acta Seismologica Sinica（in Chinese），2000，22（6）：568－576.

［18］ Sornette D，Pisarenko V F.Fractal plate tectonics.Geophys.Res.Lett.，2003，30：1105，doi：10.1029／2002＿GL＿015043.

［19］ Ouillon G，Sornette D.Search for direct empirical spatial correlation signatures of the critical triggering earthquake model.Geophys.J.Int.，2004，157（3）：1233－1246.

［20］ 高祥林，罗焕炎，诺依格鲍尔H J.大陆碰撞动力学的三维数值模拟.地震地质，1987，9（2）：65－73.Gao X L，Luo H Y，Neugebauer H J.Three dimensional numerical modeling for the dynamics of the continental collision.Seismology and Geology（in Chinese），1987，9（2）：65－73.

［21］ 张东宁，许忠淮.青藏高原现代构造应力状态及构造运动的三维弹粘性数值模拟.中国地震，1994，10（2）：136－143.Zhang D N，Xu Z H.Three dimensional elasto－visco numerical simulation of Qinghai－Xizang Plateau′s recent tectonic stress field and its motion.Earthquake Research in China（in Chinese），1994，10（2）：136－143.

［22］ 王绳祖，张四昌，田勤俭.大陆动力学：网状塑性流动与多级构造变形.北京：地震出版社，2001：15－20.Wang S Z，Zhang S C，Tian Q J.Continental Dynamics：Netlike Plastic－Flow and Hierarchical Tectonic Deformation（in Chinese）.Beijing：Seismological Press，2001：15－20.

［23］ 臧绍先，宁杰远，景志成.俯冲带流变性质的研究.中国科学（D辑），2001，31（9）：705－711.Zang S X，Ning J Y，Jing Z C.Study on plastic－flow characteristics in subduction belt.Science in China（Series D）（in Chinese），2001，31（9）：705－711.

［24］ 于泳，洪汉净，刘培洵等.粘弹性有限元与弹簧滑块耦合模型——断层与地块相互作用的数值模拟.中国科学（D辑），2003，33（增刊）：82－90.Yu Y，Hong H J，Liu P X，et al.The viscoelastic finiteelement and the coupling model of the spring－sliding black——numerical simulation on the interaction between faults with the plate.Science in China（Series D）（in Chinese），2003，33（Suppl.）：82－90.

［25］ 沈正康，万永革，甘卫军等.东昆仑活动断裂带大地震之间的黏弹性应力触发研究.地球物理学报，2003，46（6）：786－795.Shen Z K，Wan Y G，Gan W J，et al.Viscoelastic triggering among large earthquakes along the east Kunlun fault system.Chinese J.Geophys.（in Chinese），2003，46（6）：786－795.

［26］ 沈正康，万永革，甘卫军等.华北地区700年来地壳应力场演化与地震的关系研究.中国地震，2004，20（3）：211－228.Shen Z K，Wan Y G，Gan W J，et al.Crustal stress evolution of the last 700years in North China and earthquake occurrence.Earthquake Research in China（in Chinese），2004，20（3）：211－228.

［27］ 万永革，沈正康，曾跃华等.唐山地震序列应力触发的粘弹性力学模型研究.地震学报，2008，30（6）：581－593.Wan Y G，Shen Z K，Zeng Y H，et al.Study on visco－elastic stress triggering model of the 1976Tangshan earthquake sequence.Acta Seismologica Sinica（in Chinese），2008，30（6）：581－593.

［28］ 邵志刚，周龙泉，蒋长胜等.2008年汶川Ms8.0地震对周边断层地震活动的影响.地球物理学报，2010，53（8）：1784－1795.Shao Z G，Zhou L Q，Jiang C S，et al.The impact of Wenchuan Ms8.0earthquake on the seismic activity of surrounding faults.Chinese J.Geophys.（in Chinese），2010，53（8）：1784－1795.

［29］ 蒋海昆，郑建常，吴琼等.中国大陆中强以上地震余震分布尺度的统计特征.地震学报，2007，29（2）：151－164.Jiang H K，Zheng J C，Wu Q，et al.Statistical features of aftershock distribution size for moderate and large earthquakes in Chinese mainland.Acta Seismologica Sinica（in Chinese），2007，29（2）：151－164.

［30］ Aki K.Earthquake mechanism.Tectonophysics，1972，13（1－4）：423－446.

［31］ Hanks T C，Bakun W H.A bilinear source－scaling model for M－logA observations of continental earthquakes.Bull.Seism.Soc.Am.，2002，92（5）：1841－1846.

［32］ Venkataraman A，Kanamori H.Observational constraints on the fracture energy of subduction zone earthquakes.J.Geophys.Res.，2004，109：B05302，doi 10.1029／2003JB002549.

［33］ Hardebeck J L，Aron A.Earthquake stress drops and inferred fault strength on the Hayward fault，east San Francisco Bay，California.Bull.Seism.Soc.Am.，2009，99（3）：1801－1814.

［34］ McGarr A，Fletcher J B.Mapping apparent stress and energy radiation over fault zones of major earthquakes.Bull.Seism.Soc.Am.，2002，92（5）：1633－1646.

［35］ Abercrombie R E.Earthquake source scaling relationships from－1to 5 MLusing seismograms recorded at 2.5km depth.J.Geophys.Res.，1995，100（24）：15－24，36.

［36］ Bayrak Y，Yilmazturk A.Stress drop and classification of global earthquakes.／／Second Balkan Geophysical Congress and Exhibition.Istanbul，1999.

［37］ Shaw B E.Constant stress drop from small to great earthquakes in magnitude－area scaling.Bull.Seism.Soc.Am.，2009，99（2A）：871－875.

［38］ Moghaddam H，Fanaie N，Motazedian D.Estimation of stress drop for some large shallow earthquakes using stochastic point source and finite fault modeling.Transaction A：Civil Engineering，2010，17（3）：217－235，Sharif University of Technology，June 2010.

［39］ Ouillon G，Sornette D.Magnitude－dependent Omori law：Theory and empirical study.J.Geophys.Res.，2005，110：B04306，doi：10.1029／2004JB003311.

［40］ 徐锡伟，陈桂华，于贵华等.5.12汶川地震地表破裂基本参数的再论证及其构造内涵分析.地球物理学报，2010，53（10）：2321－2336.Xu X W，Chen G H，Yu G H，et al.Reevaluation of surface rupture parameters of the 5.12Wenchuan earthquake and its tectonic implication for Tibetan uplift.Chinese J.Geophys.（in Chinese），2010，53（10）：2321－2336.

［41］ 王卫民，赵连锋，李娟等.四川汶川8.0级地震震源过程.地球物理学报，2008，51（5）：1403－1410.Wang W M，Zhao L F，Li J，et al.Rupture process of the Ms8.0Wenchuan earthquake of Sichuan，China.Chinese J.Geophys.（in Chinese），2008，51（5）：1403－1410.

［42］ 郭启良，王成虎，马洪生等.汶川Ms8.0级大震前后的水压致裂原地应力测量.地球物理学报，2009，52（5）：1395－1401.Guo Q L，Wang C H，Ma H S，et al.In－situ hydro－fracture stress measurement before and after the Wenchuan Ms8.0 earthquake of China.Chinese J.Geophys.（in Chinese），2009，52（5）：1395－1401.

The spatio－temporal features of earthquake stress perturbation based on the simplified two－layer viscoelastic medium model

JIANG Hai－Kun1，WU Qiong1，SONG Jin1，LI Jin2，QU Jun－Hao3
1 China Earthquake Networks Center，Beijing100045，China
2 Institute of Earthquake Science，China Earthquake Administration，Beijing100036，China
3 Institute of Geology，China Earthquake Administration，Beijing100029，China

Based on the simplified two－layer viscoelastic medium model and its temporal characteristics of the deformation process，considering the joint action of the instantaneous elastic stress perturbation in the upper layer（more elastic）and the delayed and long－term load on upper layer due to the viscous relaxation deformation in lower layer（more viscous），the spatio－temporal variation of the earthquake stress perturbation has been studied.The results show that the stress perturbation increases quickly during a short time since the earthquake and then decays slowly for a long time.And when model parameters approach to real data more and more，the increasing anddecay process of the stress perturbation is slower，and the duration becomes gradually longer.In another word，the earthquake activity has a long－term‘memory’feature.Therefore，the longterm influence of stress perturbation could not be ignored in the study of earthquake activity or Coulomb stress changes.The stress perturbation has a limited acting range in space.It decreases obviously with distance inside the range，the decay is quick nearby the epicenter and is slow far away from the epicenter.The stress perturbation could be ignored outside the range.For the model parameters used in this paper，which approach to the real status for some extent，the effective acting range of the stress perturbation is about 2.5times of the linear fracture size of the earthquake.The stress perturbation increases gradually with the mainshock magnitude，for the assumed model parameters in this paper，it increases more quickly when magnitude is larger than M6.The relative error of stress perturbation，resulting from the measurement errors of the fracture size，is relational to the fracture size（magnitude）and epicenter distance，and there is no relationship with the time.The relative error increases with the epicenter distance，but its total influence on changing tendency and numerical range of the stress perturbation are very small，it tends to constant when distance is large enough.For earthquake with magnitude M6，M7and M8，the maximum relative errors of stress perturbation are smaller than 22%，30%and 38%.

Two－layer viscoelastic medium model，Earthquake stress perturbation，Duration，Acting range，Mainshock magnitude

10.6038／j.issn.0001－5733.2012.04.019

P315

2011－02－14，2011－09－07收修定稿

国家“十一五”科技支撑计划项目（2008BAC38B03）资助.

蒋海昆，男，1964年生，博士，研究员.主要从事统计地震学研究.E－mail：jianghaikun＠sohu.com

蒋海昆，吴琼，宋金等.双层黏弹介质模型条件下地震应力扰动的时空特征.地球物理学报，2012，55（4）：1240－1248，

10.6038／j.issn.0001－5733.2012.04.019.

Jiang H K，Wu Q，Song J，et al.The spatio－temporal features of earthquake stress perturbation based on the simplified twolayer viscoelastic medium model.Chinese J.Geophys.（in Chinese），2012，55（4）：1240－1248，doi：10.6038／j.issn.0001－5733.2012.04.019.

（本文编辑 何 燕）