起伏地表采集数据的三维直接叠前时间偏移方法

张 浩，张剑锋

1中国科学院地质与地球物理研究所中国科学院油气资源研究重点实验室，北京 100029 2中国科学院研究生院，北京 100049

起伏地表采集数据的三维直接叠前时间偏移方法

张 浩1，2，张剑锋1

1中国科学院地质与地球物理研究所中国科学院油气资源研究重点实验室，北京 100029 2中国科学院研究生院，北京 100049

提出一种可对起伏地表采集的三维地震资料直接进行偏移成像的叠前时间偏移方法和流程．它用两个等效速度描述近地表和上覆层对地震波传播的影响，可对炮、检点不在同一水平面的三维地震资料直接进行叠前时间偏移处理．该方法不对近地表地震波传播做垂直出、入射假定，因此可适应高速层出露等不存在明显低、降速带情况．描述近地表和上覆层的两个等效速度参数可依据偏移道集的同相轴是否平直来确定，避免了确定近地表速度的困难；而对已知近地表速度的情况，则可进一步修正近地表速度，获得更好的成像效果．用三维起伏地表的理论数据和中国东部某工区实际数据验证了所发展方法和处理流程的有效性和实用性．

起伏地表，三维成像，近地表速度，叠前时间偏移

1 引 言

随着我国陆上油气勘探向西部和南方地区的深入，复杂地表已成为制约地震资料处理的关键因素．由于地表起伏较大、高速的老地层出露，现行的以静校正处理为基础的陆上地震资料处理方法和流程遇到困难．浮动基准面技术［1－2］可解决地表起伏较大问题，但高速层出露导致垂直入射和出射的静校正应用条件不成立，继续使用静校正方法将带来较大的误差［3］．基于波场延拓的基准面重建方法［4］可同时解决地表起伏和高速层出露问题，但这一方法是以获得准确的近地表速度模型为基础的；由于起伏地表采集的地震资料信噪比较低，获得准确的近地表速度模型是一个相当困难的任务［5］．此外，基于波场延拓的基准面重建方法导致重建数据的地震道数激增，极大地增加了后续偏移处理的计算量．

就实际中遇到的大量地质目标而言，尽管地表复杂、断层等构造断裂发育，但除近地表以外的上覆地层的速度横向变化并不是很剧烈，这就给叠前时间偏移的应用提供了可能性．叠前时间偏移的主要优点是只用一个等效速度（即均方根速度）描述地震波传播，可对一类倾角、断层较为复杂，但速度横向变化不是很剧烈的构造较好的成像［6］．独立的、单一等效速度使得叠前时间偏移的速度建模变得简单．本文进一步发展叠前时间偏移方法，通过引入第二个等效参数描述近地表地震波传播，发展可对炮、检点不在同一水平面的三维地震资料直接进行叠前时间偏移处理的成像方法，以此避免高速层出露和近地表速度建模这两个困难．

现行的直接对起伏地表采集数据进行偏移、避免使用静校正技术的直接偏移方法主要是基于叠前深度偏移算法［7－8］．这一方法需要准确的近地表速度和地下构造的层速度模型，而这两类速度又相互影响，与海上或水平地表情况下确定深度偏移的层速度模型相比，这类方法的速度建模更加困难．文献［9］尽管在计算地震波走时时引入了平均速度和均方根速度，但这两个速度是由层速度计算得到的，它们是成像点和炮点（或检波点）的函数；由于在同一成像点有多个均方根速度存在（随炮点或检波点变化），这一速度是不能如叠前时间偏移那样通过简单的扫描方式得到的，只能通过先求取层速度模型，进而解析计算得到．因此，文献［9］仍属于叠前深度偏移范畴，面临着与叠前深度偏移相同的困难．董春晖等［10］发展了一个基于双速度参数的二维直接叠前时间偏移方法，有效地将叠前时间偏移技术推广应用于起伏地表问题．此外，实际起伏地表问题总是三维的，炮、检点不在同一方位角平面，导致走时、等效偏移距（浮动基准面上的偏移距）的计算较二维情况的更复杂．本文则在确定两个等效速度参数、处理三维起伏地表这两方面提升了文献［10］的方法，并且将这一方法应用于三维起伏地表采集的实际地震资料．

本文的关键有两点，一是从叠前深度偏移的单程波方程出发，解析给出了三维情况下由描述近地表和上覆层速度的两个等效速度表达的地震波走时、幅值和等效偏移距，并发展了基于表插值的快速算法；二是发展了基于偏移道集同相轴的双曲弯曲和局部微弯曲，分别确定两个等效速度参数的方法和算法流程．文中也应用了随方位角和构造倾角变化的三维时变偏移孔径，这使得本文叠前时间偏移方法即有效地压制了偏移噪音，也减少了偏移计算量．三维起伏地表的理论数据和实际地震资料证明了本文方法和处理流程的正确和有效性．

2 走时、振幅与等效速度参数

假设三维非均匀介质可近似为层状介质，不失一般性，令炮点或检波点在坐标原点；在波数－频率域，基于三维深度偏移的相移法，该炮点或检波点的波场深度延拓可用时间深度表示为

若将第m层介质界面作为基准面，可近似式（1）中右端指数项中的相移量为

将式（2）代入（1）式并做空间傅里叶反变换，可得到空间－频率域波场：

式（3）是一个二重震荡积分，可利用稳相点原理［11］求得渐进解为

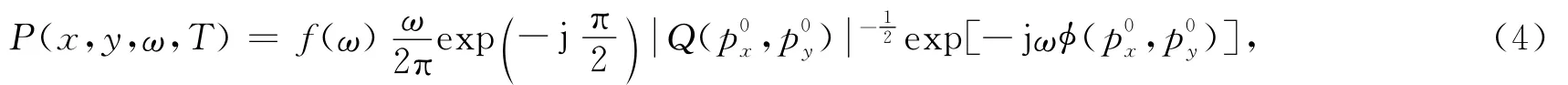
式（4）中，定义

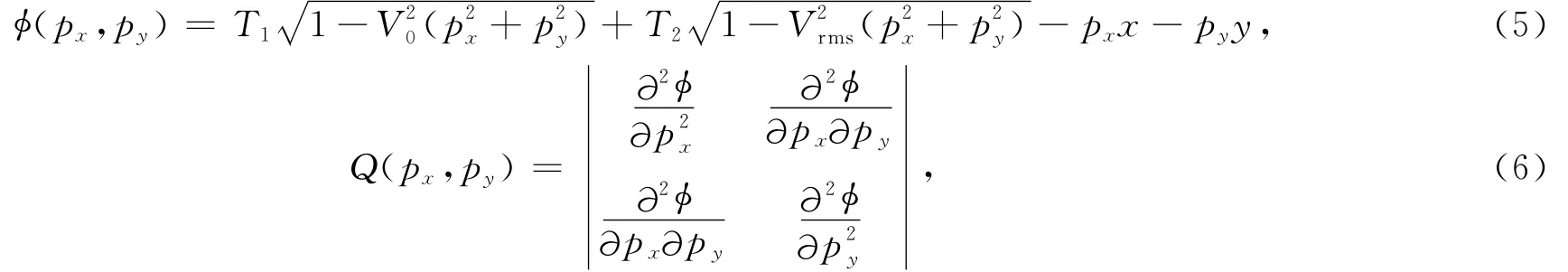
其中px和py是射线参数的零点，可由下式解得：

引入新的变量pr，定义p0x＝prcosφ，p0y＝prsinφ，其中φ是坐标点（x，y）的方位角，则（7）和（8）式可转化为单变量的方程：

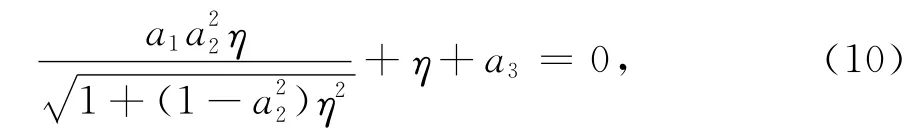
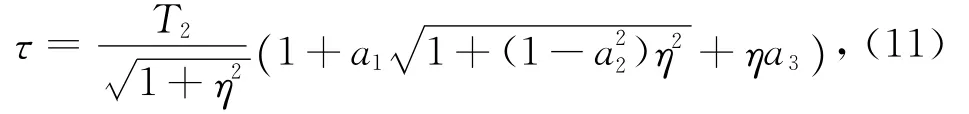
而代入式（6），则可进一步得到地震波的幅值．

令a2＝0，即假设基准面以上是明显的低速带，则式（11）简化为

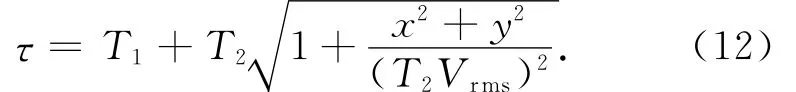
这就是应用静校正技术的走时公式．这表明式（11）涵盖了现行的静校正方法．若假定介质为上、下层速度分别是V0和Vrms的双层介质，式（9）和（11）则可由Snell定律直接导出，这从另一个角度证明了式（9）和（11）的正确性；式（9）和（11）既扩展了Snell定律的结果，也给出了非均匀介质情况下等效速度参数的物理含义．

尽管可解析求解［12］式（9），但对三维偏移过程中大量的成像点、炮点、检波点组合而言，直接计算涉及了太多的计算量．既然3个无量纲系数完全决定了式（9）的四次方程，我们发展了基于表插值的快速算法．3个无量纲系数均有明确的物理意义，就叠前时间偏移方法而言，其对大于70°角度传播的高角度波场是不感兴趣的，因此可令0≤a3≤tan70；即使高速层出露，近地表等效速度也不可能大于深层速度，因此可定义0≤a2≤1．0；叠前偏移成像更多的是关心中、深层，若假定从T2≥T1开始成像计算，则可定义0≤a1≤1．0．这样，若对这3个无量纲系数等间距离散采样，预先求解对应的η并建立一个三维表，就可在偏移过程中通过计算3个无量纲系数，直接在表中拾取对应的η．炮点至成像点和检波点至成像点可用同一个表．这一基于表的算法可极大提高三维偏移的计算效率．

尽管（9）、（11）以及（6）式的走时和振幅值是基于（1）式的层状介质假设推出的，但通过允许两个等效速度V0和Vrms以及基准面横向变化，式（9）、（11）以及（6）式的解可代表三维横向弱非均匀介质中地震波的走时和振幅值；对较强的速度横向变化情况，只能采用基于层速度模型的深度域延拓方法；文献［13］通过引入速度梯度等信息，对较强横向变速情况下的走时计算进行了讨论．

等效速度参数Vrms和基准面深度的横向变化是由成像点的横向坐标（x，y）决定的．这样，Vrms将与基准面上的等效偏移距构成常规叠前时间偏移的双曲走时关系；如果令a2＝0，则本文算法可退化为浮动基准面叠前时间偏移方法．另一个等效参数V0即可随炮、检点横向变化，也可随成像点横向变化．

3 等效速度参数估计与等效偏移距计算

第2节的研究表明，可用两个等效速度参数描述地震波在近地表和上覆层中的传播；而如何准确获得这两个等效参数，是本文方法实际应用的关键问题．本文的两个等效速度参数在每个成像点是惟一的，这两个参数完全决定了该成像点处共反射点道集（CRP）的表现，因此可在偏移过程中根据该CRP道集的表现来决定它们；不同于文献［9］的双速度参数，它们是成像点和炮点（或检波点）的函数，若干个不同的参数决定了该成像点处CRP道集的表现，因此不能由单个CRP道集来决定该速度参数．实际上，文献［9］中的双速度参数只是用于近似计算地震波的走时，它们是由已知的层速度模型解析计算得到的．

从偏移成像的角度出发，CRP道集中同相轴是否平直是确定两个等效速度的标准，这也是本文确定等效速度的出发点．但两个等效速度参数共同影响了同相轴的平直，只有区分这两者对同相轴弯曲的独特影响，才能有效地确定这两个参数．

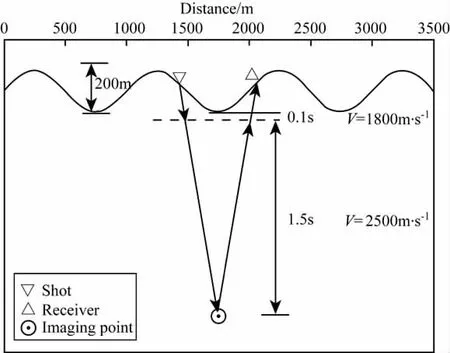
图1 等效速度参数对走时影响分析示意图Fig．1 Illustration of equivalent velocity parameter analysis using 2Dmodel including topography

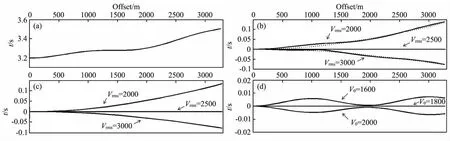
图2 等效速度参数对走时残差影响Fig．2 Influence of equivalent velocity parameters on residual traveltime

本文用一个简单的二维模型来考察两个速度参数变化对走时的影响．如图1所示，起伏地表按正弦函数变化，其波长为1000m，波锋与波谷间的高程为200m；成像点在模型中心，对应该成像点的基准面如图1中虚线所示，较地表高程曲线的波谷低0．1s（时间深度），而成像点在基准面下1．5s处；基准面上、下的介质是均匀的，速度分别为1800m／s和2500m／s．图2a给出了由（11）式求得的地面上炮点至成像点再反射到地表检波点的地震波走时随偏移距（水平距离）的变化曲线．若令V0＝1800m／s，Vrms＝2000，2500，3000m／s，利用式（11）做动校正，可得剩余走时曲线（如图2b），而图2c则给出了随基准面上的等效偏移距变化的剩余走时曲线；图2b中的点线是最佳拟合剩余走时的双曲线，而图2c的点线与剩余走时曲线的实线重合．观察图2b和图2c可发现，速度参数Vrms影响了同相轴的整体弯曲程度，而等效偏移距使得这种弯曲更好地展现了如常规时间偏移的双曲特征．若令V0＝1600，1800，2000m／s，Vrms＝2500m／s，利用式（11）做动校正，可得剩余走时曲线（如图2d）．观察图2d可发现，不准确的速度参数V0在产生同相轴的小幅度弯曲的同时，导致了同相轴的局部绕曲．因此，CRP道集中同相轴的局部微弯曲是确定V0的指标，而整体的双曲弯曲可指示速度参数Vrms的正确与否．实际应用中，同相轴的局部微弯曲可通过叠加道波形的宽窄来判断，而双曲弯曲使得可用常规的NMO方法拾取剩余速度．

上述讨论表明，基准面上的等效偏移距对确定速度参数是重要的；而三维起伏地表情况，特别是炮、检点不在同一方位角平面上时，等效偏移距的计算较二维情况变的更复杂．图3给出了三维情况下等效偏移距的示意图，图中S和G点分别代表起伏地表上的炮点和检波点，AOB平面代表基准面，I代表成像点．采用常规静校正方法时，地震道的偏移距不变，如图中的PQ；而本文方法考虑了地震波的实际传播路径，基准面上的真实（等效）偏移距应是MN．

已由式（9）或（10）求得由S传至M再传至I点的地震波的射线参数pr．对M传至I点的地震波应用式（10）（可认为T1为零），地震波的射线参数pr不变，则简单得到

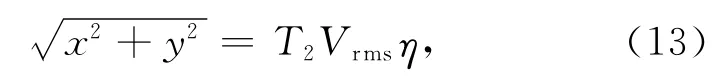
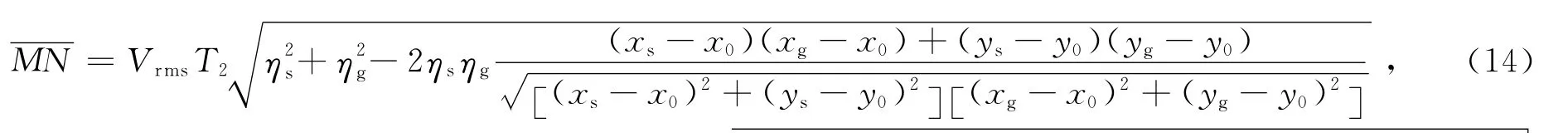
式中（xs，ys）是炮点水平坐标，（xg，yg）是检波点水平坐标，（x0，y0）是成像点水平坐标，ηs和ηg分别是根据炮点和检波点信息由表中拾取的η．式（14）表明利用基于表插值的快速算法可在得到走时和幅值的同时，得到等效偏移距；图3中曲线SMI和GNI代表非均匀介质中地震波的传播路径，因此式（14）可适用于非均匀介质．

图3 等效偏移距示意图Fig．3 Illustration of equivalent offset on the datum

实际应用中等效参数V0的估计有两种情况：一是地表调查、微测井、折射或层析静校正等方法已给出了较准确的近地表速度场；二是尚没有做上述工作．对于第一种情况，令等效参数V0横向通过较小的百分比扫描，根据各水平位置处剩余动校后叠加道波形的宽窄和道集的情况综合确定各水平位置处的最佳百分比参数，对百分比参数横向平滑，用平滑后的百分比参数修正近地表速度，即得到等效参数V0．对第二种情况，可以估计几个近地表速度对最小偏移距数据进行偏移，观察最小偏移距的成像情况确定一个初始的等效参数V0，再将等效参数V0做速度百分比扫描，根据各水平位置处剩余动校后叠加道波形的宽窄和道集情况确定各水平位置处新的V0，横向平滑后即是最终的近地表速度场．评估叠加道波形的宽窄时应综合考虑几个不同深度的同相轴．

等效参数Vrms可根据求得的等效偏移距，在偏移形成的CRP道集上，利用常规的NMO技术拾取．详见第5节的数据处理流程．

4 三维偏移与成像幅值权系数

基于式（10）的查表法仅给出炮点至成像点和检波点至成像点的走时和振幅值；而偏移的目的是进一步得到地下界面的反射系数图像．若将单个地震道看作是仅有一个接收道的单炮记录，则根据（4）式和基于（10）式的表插值算法，可分别得到炮域偏移的下行波场和反传波场：

式中假设震源是一时间脉冲，f（ω）是接收信号的傅里叶变换．将式（15）代入波动方程叠前深度偏移的反褶积成像条件［14］，有成像结果

式中F′（t）是f（ω）对应的时域函数的一阶导数．式（16）的成像结果表明，对任一单道数据，对数据求一阶导数；对成像区域的每一成像点，计算走时ts＋tg和成像权系数Ag／As；在数据的一阶导数上拾取ts＋tg时刻的振幅值并乘上权系数，即完成该道数据的成像．

对全部地震道做上述操作，将成像结果累加，即完成了全部数据的成像．不同于忽略权系数的现行方法，式（16）的权系数Ag／As实现了正确补偿地震波的几何扩散效应，使得深层成像更清晰．

5 偏移流程

本文偏移流程的关键是在偏移过程中确定两个等效速度V0和Vrms，偏移流程如下：

1．综合地表起伏情况、可能的地表信息和最小偏移距剖面，确定一个光滑的定浮动基准面；

2．对地表调查、微测井、折射或层析静校正等方法已给出了较准确的近地表速度场情况，使用该速度场作为初始V0；对无此类信息情况，根据经验确定一均匀速度作为初始；

3．根据V0，在几个典型CDP位置，将CMP道集静校正到浮动基准面，利用NMO确定初始；

4．对未经静校正处理的数据，依据初始V0和Vrms做式（16）的偏移计算，计算等效偏移距，形成等效偏移距下的共反射点道集；

5．利用初始Vrms，对共反射点道集做反动校，再做NMO动校拾取速度，对拾取的速度做空间平滑，作为新的Vrms；

6．利用初始V0和新的Vrms，对V0做百分比扫描，对较疏的CDP位置和主要的同相轴区域做局部偏移计算，利用第3节讨论的方法确定新的V0；

7．在新的V0和Vrms下重新进行偏移计算，形成等效偏移距下的共反射点道集．若剩余动校正量较小，进行剩余动校正、切除和叠加，得到最终偏移剖面；若剩余动校正量较大，利用Vrms做反动校，再做动校，形成再次更新的Vrms，对V0和Vrms重复上述过程，得到最终偏移剖面；

8．由于浮动基准面一般是非水平的，基于浮动基准面的偏移成像将扭曲地下构造图像．计算浮动基准面与选定的水平基准面的垂直走时，用这一时间修正偏移图像，可得到基于水平基准面的偏移剖面．

6 数值算例

为了验证本文方法的正确性和工业应用的可能性，分别应用本文方法处理了三维起伏地表采集的理论模型数据和我国东部某工区的实际三维起伏地表采集资料，前者证明了本文理论和方法的正确性，后者表明了本文方法具有实际工业应用价值．

6．1 三维起伏地表模型数据

三维起伏地表模型数据由东方地球物理公司提供．该数据近地表高程变化明显，地表不存在明显的降低速带，图4是模拟该数据集用到的速度模型在inline和crossline方向的切片，实线表示地表高程，最大高差达到590m，虚线是本文采用的浮动基准面．该理论数据集共3940炮，每炮10条线接收，每条线201道，每炮共2010道，中间放炮，两边接收．inline方向道间距40m，crossline方向线距100m，最小偏移距50m，最大偏移距5100m，记录总长度为5s，采样率为4ms．图5是该三维数据的典型单炮记录，从中可以看到：炮记录中的波场已被严重扭曲，同相轴不再是水平地表情况下的双曲线．图6给出了使用本文方法得到的最终偏移结果．5个界面的反射同相轴被很好的成像，成像结果与速度模型在形状上不完全对应是因为成像结果是时间剖面，这也是时间偏移的特点．由于利用了成像权系数，不用AGC深层构造也得到了较好的成像；第5个同相轴较弱是该层的速度对比很小（见图4速度模型），陡界面成像不好是因为地震记录的偏移距较小，导致不能接收到陡界面的反射信号所致．

图4 三维理论数据速度模型，地表高程（实线），浮动基准面（虚线）Fig．4 Velocity model，surface elevation（solid）and floating datum（dot）of 3Dsynthetic data

图5 三维理论数据典型单炮记录Fig．5 Typical shot record of 3Dsynthetic data

图6 三维理论数据直接叠前时间偏移剖面Fig．6 Direct prestack time migration result of the 3Dsynthetic data

该理论模型尽管简单，但由于地表不存在明显的降低速带，应用常规的静校正加浮动基准面方法是不能正确成像的．

6．2 三维起伏地表实际数据

本节进一步给出了应用本文方法处理某工区三维实际数据的例子．图7是该工区地表高程的等值线图，可见地表起伏变化是较剧烈的．三维资料共1710炮，每炮16线接收，每线142道，道距40m，线距120m，中间放炮，记录长度为6s，采样率为4ms．该三维资料经过压制面波等去噪处理，但没有进行静校正处理．图8显示了典型的单炮记录，地表起伏导致的同相轴错动明显可见．图9给出了在两个等效速度参数进行更新过程中，典型共反射点道集中同相轴的变化情况，随着速度参数的更新，同相轴变得更加平直和清晰．

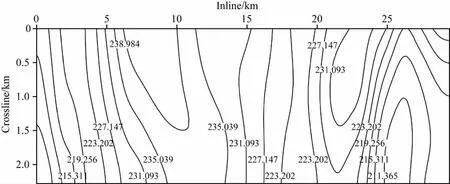
图7 三维实际数据地表高程Fig．7 Surface elevation of the 3Dfield data

我们没有得到该工区地表速度的任何资料，因此凭经验选取1800m／s作为初始．图10是更新前后在一条inline线上的速度对比情况，图11是最终得到的在一条inline线上的分布图．图12是在一条inline线上的偏移叠加剖面，同相轴连续性较好，断层断点清晰，原始资料中的同相轴错动被消除，这表明本文方法在偏移过程中正确地处理了起伏地表影响，实现了直接偏移．

本文偏移处理是在没有任何近地表速度资料的情况下进行的，这表明本文方法具有了自主建立近地表和上覆层速度的能力．

7 结 论

图8 典型三维单炮记录中单条测线的接收信号Fig．8 Seismic signature of one receiver line with respect to 3Dfield data

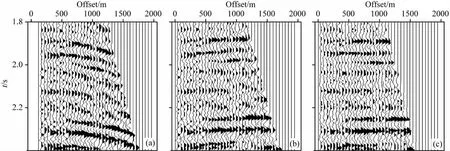
图9 CRP道集随着速度更新的变化情况Fig．9 Changes in CRP gather while updating the velocities

图10 Inline方向速度参数V0更新情况Fig．10 Comparison between initial and updated V0parameter in inline

图11 Inline方向速度参数Vrms更新结果Fig．11 Updated parameter Vrmsin inline

本文提出了一种可对起伏地表采集的三维地震资料直接进行偏移成像的叠前时间偏移方法和流程．该方法可适应高速层出露等不存在明显低、降速带的情况，能在偏移过程中自主建立（或修正）近地表速度模型和偏移使用的叠加速度模型．三维理论模型数据证明了方法的正确性和其处理近地表不存在明显低、降速带情况的能力．未经静校正处理的三维实际陆上资料的直接偏移结果表明，本文方法具有很好的工业化应用能力．即使不考虑高速层出露，仅从避免了初至拾取、近地表速度建模等繁杂的静校正流程而言，本文方法就有很好的实用价值．本文方法为我国陆上油气勘探面临的复杂地表问题指示了一个具有工业应用价值的有效途径．

图12 实际数据直接叠前时间偏移叠加剖面的inline切片Fig．12 Stack section of direct prestack time migration in inline of 3Dfield data

（References）

［1］ Sun C W，Jing P G，Pu Y．Seismic imaging in the mountainous area of Southern China：Statics correction compared with migration from topography．SEG expanded abstract，2009．

［2］ 刘国峰，刘洪，李博等．山地地震资料叠前时间偏移方法及其GPU实现．地球物理学报，2009，52（12）：3101－3108．Liu G F，Liu H，Li B，et al．Method of prestack time migration of seismic data of mountainous regions and its GPU implementation．Chinese J Geophys．（in Chinese），2009，52（12）：3101－3108．

［3］ Cox M．Static Corrections for Seismic Reflection Surveys．Tulsa：Society of Exploration Geophysics，1999．

［4］ Bevc D．Flooding the topography：Wave－equation datuming of land data with rugged acquisition topography．Geophysics，1997，62（5）：1558－1569．

［5］ Kelamis P G，Erickson K E，Verschuur D J，Berkhout A J．Velocity－independent redatuming：A new approach to the near－surface problem in land seismic data processing．The Leading Edge，2002，21（8）：730－735．

［6］ Black J L，Brzostowski M A．Systematics of time－migration errors．Geophysics，1994，59（9）：1419－1434．

［7］ Reshef M．Depth migration from irregular surfaces with depth extrapolation methods．Geophysics，1991，56（1）：119－122．

［8］ Rajasekaran S，McMechan G A．Prestack processing of land data with complex topography．Geophysics，1995，60（6）：1875－1886．

［9］ Wiggins J W．Kirchhoff integral extrapolation and migration of nonplanar data．Geophysics，1984，49（8）：1239－1248．

［10］ 董春晖，张剑锋．起伏地表下的直接叠前时间偏移．地球物理学报，2009，52（1）：239－244．Dong C H，Zhang J F．Prestack time migration including surface topography．Chinese J．Geophys．（in Chinese），2009，52（1）：239－244．

［11］ 李世雄．波动方程的高频近似与辛几何．北京：石油工业出版社，2001．Li S X．Wave Equation with High Frequency Approximation and Symplectic Geometry（in Chinese）．Beijing：Petroleum Industry Press，2001．

［12］ Zhang J F，Verschuur D J，Wapenaar C P A．Depth migration of shot records in heterogeneous，transversely isotropic media using optimum explicit operators．Geophysical Prospecting，2001，49（3）：287－299．

［13］ 张廉萍，刘洪，李幼铭．单程波李代数深度积分的精度分析和算法改进．地球物理学报，2010，53（11）：2739－2746．Zhang L P，Liu H，Li Y M．The precision analysis and algorithm improvement in Lie algebra depth integral of oneway seismic wave．Chinese J．Geophys．（in Chinese），2010，53（11）：2739－2746．

［14］ 张宇．振幅保真的单程波方程偏移理论．地球物理学报，2006，49（5）：1410－1430．Zhang Y．The theory of true amplitude oneway wave equation migration．Chinese J．Geophys．（in Chinese），2006，49（5）：1410－1430．

3Dprestack time migration including surface topography

ZHANG Hao1，2，ZHANG Jian－Feng1

1 Key Laboratory of Petroleun Resources Research，Institute of Geology and Geophysics，Chinese Academy of Sciences，Beijing100029，China 2 Graduate University，Chinese Academy of Sciences，Beijing100049，China

We present a 3Dprestack time migration scheme and workflow that can image land seismic data without datum static corrections．The scheme mimics the influences of the nearsurface and overlay on wave propagation using two equivalent velocities．As a result，it is not necessary for wave path to be vertical incidence in the near－surface，as in conventional static corrections．This leads to the proposed scheme which can handle the more complex surface cases，such as the exposure of high velocity in the near－surface．The proposed scheme can update the two equivalent velocities with respect to the flats and consistency of the events．A synthetic 3D dataset and a field 3Ddataset without datum static corrections are used to demonstrate the scheme and the workflow．

Topography，3Dimaging，Near－surface velocity，Pre－stack time migration

P631收修定稿2010－12－16，2012－01－17收修定稿

国家自然科学基金重点项目（40930422）和国家科技重大专项（2011ZX05008－006）资助．

张浩，男，1983年生，中国科学院地质与地球物理研究所博士研究生，主要从事叠前偏移成像研究．E－mail：zhanghao＠mail．iggcas．ac．cn

张浩，张剑锋．起伏地表采集数据的三维直接叠前时间偏移方法．地球物理学报，2012，55（4）：1335－1344，

10．6038／j．issn．0001－5733．2012．04．029．

Zhang H，Zhang J F．3Dprestack time migration including surface topography．Chinese J．Geophys．（in Chinese），2012，55（4）：1335－1344，doi：10．6038／j．issn．0001－5733．2012．04．029．

10．6038／j．issn．0001－5733．2012．04．029

（本文编辑 汪海英）