电性参数分块连续变化二维MT有限元数值模拟
2012-12-15王绪本
刘 云,王绪本
油气藏地质及开发工程国家重点实验室,成都理工大学,成都 610059
电性参数分块连续变化二维MT有限元数值模拟
刘 云,王绪本*
油气藏地质及开发工程国家重点实验室,成都理工大学,成都 610059
为了易于模拟野外复杂地形和地下任意形状地电体模型,将有限元单元网格设计为三角单元;并考虑到野外实际勘探中,地球介质的电性参数均是连续变化的情况,单元内的场值和电性参数被设计为双线性变化;推导出二维起伏地形条件下大地电磁法有限元数值模拟算法;根据单元节点主场值和线性插值形函数间的关系,计算出单元节点的辅助场值;在二维起伏地形情况下,定义TE、TM模式视电阻率和阻抗相位.4个模型的计算的结果与解析法的均方根误差小于1%,地形模拟与前人的计算结果相符,模拟倾斜界面异常体,能有效的反映出其异常形态.
大地电磁法,起伏地形,三角单元网格,电性参数分块连续变化,有限元
1 引 言
大地电磁法(MT)已广泛应用于地球物理探测各个领域.我国的山区面积比较大,在起伏地形条件下开展MT工作时,地形的影响产生电磁场畸变,这给资料处理和解释工作带来很大困难,因此有必要研究带地形的MT数值模拟算法.
目前,在二维起伏地形和地电模型条件下,国内外学者采用过多种有限元剖分方式的二维MT有限元数值模拟.在有限元电性参数(如电导率、传播系数 等)分 块 均 匀 的 前 提 下,Wanna maker[1]、Mauriello等[2]采用矩形三角网格剖分、双线性插值有限元进行数值模拟,陈小斌[3-4]、谢飞[5]用自适应地形三角网格剖分、双线性插值有限元数值模拟,周熙襄[6]、王绪本[7]、刘云等[8]采用自适应地形四边形网格剖分、双二次插值有限元数值模拟,对斜坡型地形产生的地形影响做模拟和分析;认为电性参数分块均匀的模拟方式,在单元块内的电性参数分布是均匀的,单元块与单元块之间的电性参数分布则不一定是连续的.但是在野外实际中,岩石、矿物的电性参数往往是变化的,因此采用电性参数分块连续变化的数值模拟方法,更符合野外实际.徐世浙、李予国等[9-10]采用矩形网格剖分,进行电性参数分块连续变化、双线性插值、双二次插值等有限元数值模拟;对于矩形网格剖分,如果在有限元矩形单元块内或单元节点处填入空气介质,从而形成台阶型地形模拟地形影响[11-12],是有其局限性的[4,13].
阮百尧[14]在起伏地形二维直流电阻率法正演数值模拟中,采用矩形内三角网格剖分、电导率分块连续变化、双线性插值有限元数值模拟.本文在此基础上,导出了起伏地形三角单元网格剖分电性参数分块连续变化的二维MT有限元数值模拟方法.
2 二维MT变分问题
如图1所示,假设三维地质模型的电、磁等参数沿构造方向(x方向)上无变化,这时可将三维模型问题转化为二维模型问题进行处理.此时,与二维MT边值问题相应的变分问题[13]是
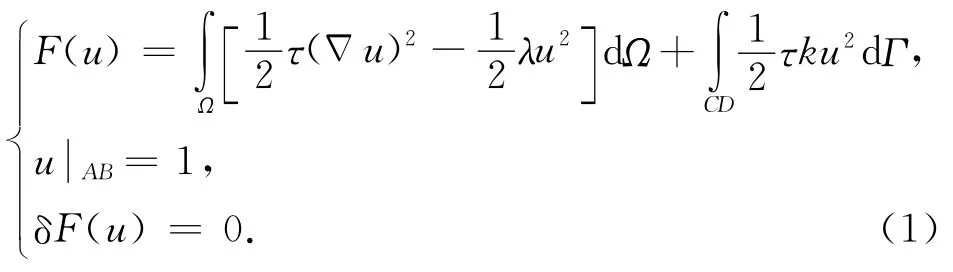
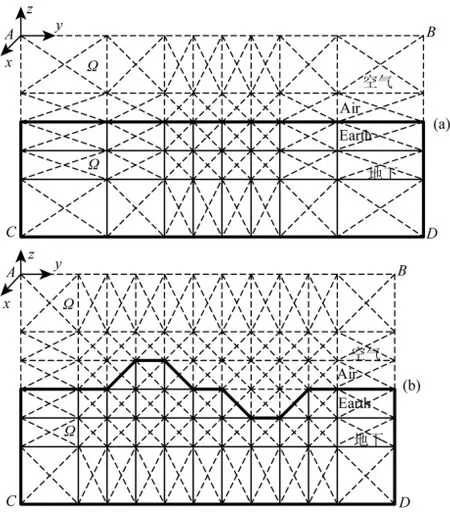
图1 区域Ω有限元网格剖分Fig.1 Division of region Ω with FEM grids
式(1)中,u为Ex或Hx,Ω为二维研究区域.
对于TE模式(Ex型):上边界AB处离地面足够远.则
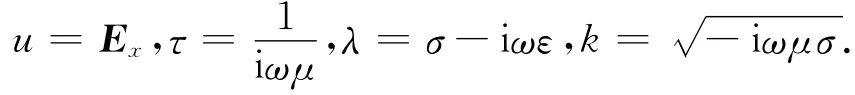
对于TM模式(Hx型):上边界AB在地面上.则

其中,σ和μ分别为介质电导率和磁导率,ω为圆频率,ε为介电常数.下边界CD处离目标区域足够远,这时σ为CD 处均匀介质电导率;左、右边界AC、BD离目标区域足够远.
3 有限单元法
用有限单元法求解式(1)的二维 MT变分问题,具体步骤如下:
3.1 网格剖分
对于TE模式,在高频时,空气介质中位移电流的影响不可忽略[3],因此研究区域为空气和地下;对于TM模式,场值Hx在空气中近似为常数(在y和z方向的偏导数近似为零),即不考虑空气介质中位移电流的影响,此时AB边界设在地面上,研究区域为地下.
如图1所示,研究区域Ω用三角单元进行网格剖分.如图1a所示,当模拟水平地形时,考虑到地下介质体形状的任意性,首先对研究区域进行矩形网格剖分,再在每一个矩形网格内剖分出4个三角单元网格.这样,一方面,避免了三角网格过于尖锐的情况;另一方面,可利用三角形的斜边模拟地形线和任意介质体倾斜的界面;如图1b所示,当模拟起伏地形时,在图1a网格剖分的基础上,地空边界采用沿实际地形线进行网格剖分.
3.2 线性插值
如图2所示,假设三角单元e内电磁场u和电性参数τ,λ,k呈线性变化,则在每一个单元中:
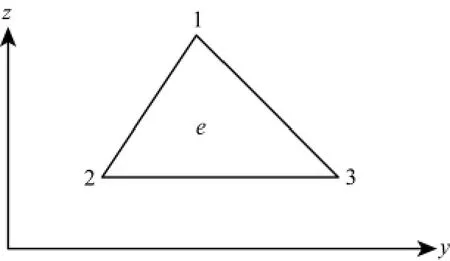
图2 三角单元eFig.2 Triangle element e

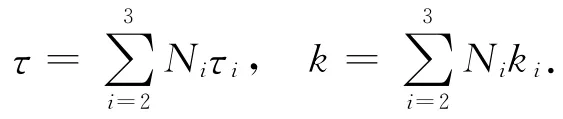
这里,ui为三角单元节点处的电磁场,τi、λi、ki为三角单元节点处的电性参数,(i)、1、2和3为三角单元的三角节点号.是关于y和z的 线 性 插 值 形 函 数 (i=1,2,3),其 中Δ =是三角单元的面积,其中
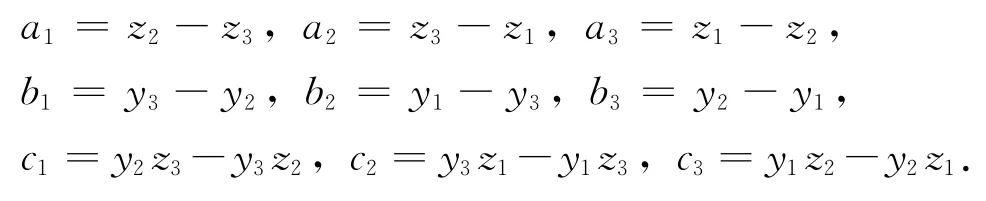
其中,(y1,z1)、(y2,z2)和(y3,z3)是三角单元节点号的坐标.
3.3 单元分析
在整个研究区域Ω中,将泛函(1)式离散化,表示为所有三角单元e的线性组合,即

3.3.1 单元分析1
u对y求偏导数,有
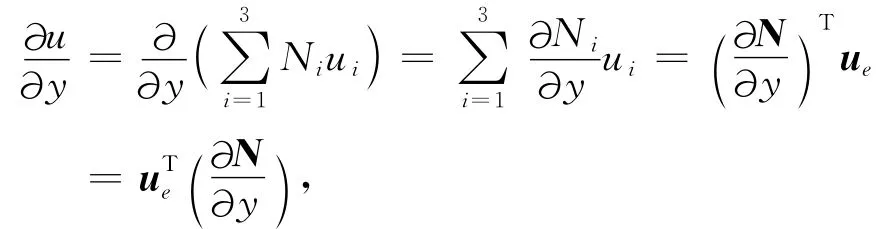

3.3.2 单元分析2
因此,对于(2)式中第二个积分项,有
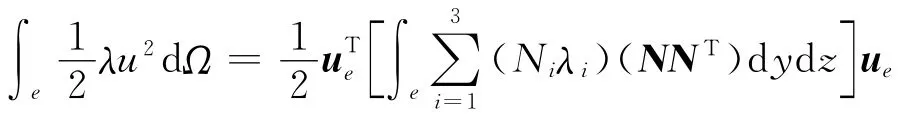
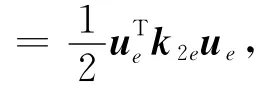
其中,c11= (6 22)λ,c12= (2 21)λ,c13=(2 12)λ,c21= (2 21)λ,c22= (2 62)λ,c23= (1 22)λ,c31= (2 12)λ,c32= (1 22)λ,c33= (2 26)λ,λ= (λ1λ2λ3)T.
3.3.3 单元分析3

3.4 系数矩阵总体合成及求变分
将研究区域Ω内每个单元系数矩阵ke按照总体节点号进行扩展,得到,相加得到总体系数矩阵K,即
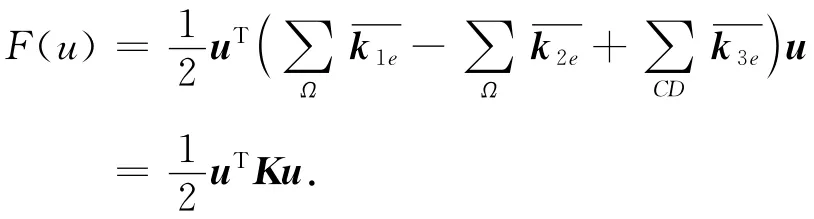
如图3所示,采用矩形内三角网格剖分方式,比较矩形网格剖分来说,增加了一个中间节点5,大大增加了计算量.但是节点5只与该矩形内4个角点有关系,而与其它不相邻的矩形网格没有任何直接联系,所以在单元分析中,运用高斯消元法事先可消去这个节点.节点5只是一个虚设的节点,并不包含在总体节点数中.到解方程结束后,亦可根据矩形网格内4个角点的已知场值和节点系数之间的关系,直接计算出节点5的场值.这样,一方面不增加节点总数,节省了计算量,另一方面每个三角单元仍具有
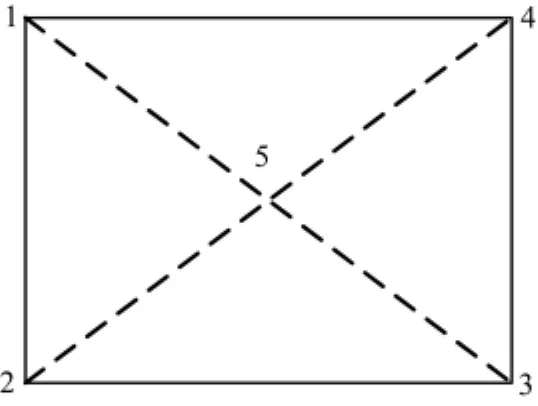
图3 矩形内节点间的关系Fig.3 Relationship of nodes in the rectangle
各自的不同物性.具体做法为:节点5的消除,将ki,j(i,j = 1,2,3,4,5)替 换 为节 点 5 的 恢 复,u5=
4 辅助场、视电阻率和阻抗相位的计算
4.1 辅助场的计算
辅助场是通过计算主场值沿某方向的方向导数得到的[17-19].当各节点主场值求出后,由3.2节可知,单元内场值u可表示为则u对y求偏导数,得
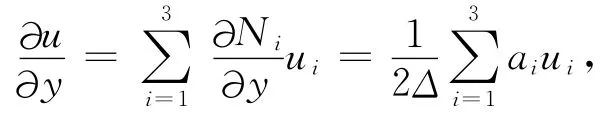
其中a1、a2、a3,是与三角单元的三顶点坐标有关的常数,所以在单元内,u的偏导数是常数.
同理可得

在大地电磁法的数值模拟中,常以地面三角单元边上任意点或三角单元的节点为实际测量点,此时要考虑到相邻单元间场值偏导数的不连续性问题[13].对于彼此相邻的单元、相同单元边或节点上场值的偏导数,可以在所属不同单元中予以分别计算,再取平均值.本文以地面三角单元的节点为实际测量点.不难发现,对于TE模式,需要计算同一测点的地表和地表上一空气层所有单元的场值偏导数,再取平均值;而对于TM模式,则只需求出同一测点的地表所有单元的场值偏导数,再取平均值即可.
4.2 视电阻率定义和阻抗相位的计算
对于TE模式:u=Ex,辅助场在二维起伏地形条件下,Ex、Hy在野外实际中均可测得,因此,视电阻率的定义仍采用普遍形式的阻抗定义方式,即
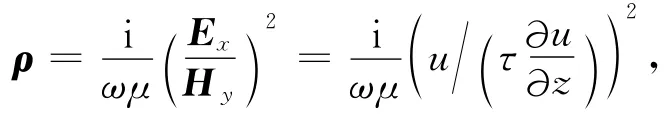
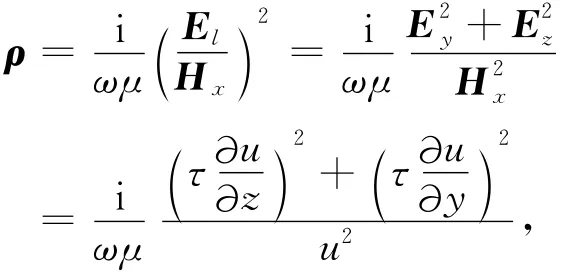
5 模型计算
为验证本文正演算法的有效性,首先与水平层状一维连续介质理论模型的解析法、以及前人已有地形模型做计算分析,之后用该算法对倾斜界面异常体模型做计算分析.
在以下所有模型的计算中,有限元网格的剖分方法如下:如图1所示,在横向网格中,目标区域采用等间隔网格,间隔距等于点距.左、右稀疏网格数各为18个,网格大小等于点距乘以系数,其中18个系数依次分别为1,1,1,1,1,2,2,2,2,4,4,4,8,8,16,32,64,128;在纵向网格中,空气稀疏网格坐标(TM模式无空气网格,单位为m)14个,依次分别为100000,50000,10000,5000,1000,500,200,100,55,35,25,15,10,5.地下网格的剖分,从1~10层的网格大小(单位为 m)依次分别为5,5,5,5,10,10,10,15,15,20,第1层网格大小的默认值为5m.当然,也可以任意设置第1层网格大小,这样,从1~10层的网格大小则相应地等比例放大或缩小.从11层及以下的网格剖分为等比网格,该层的网格大小等于上一层网格大小乘以等比系数,等比系数一般为1.1或1.2.这样,横向网格数则取决于测点数的多少,纵向网格数则取决于探测深度的选择;当模拟起伏地形时,上、下地表附近还要加上地形网格,地形网格数等于所有测点的高程数(对于重复的高程,只计1个),地形网格大小等于相邻高程之差.
5.1 一维连续介质模型
如图4所示,三层一维连续介质地电断面模型,第一层电阻率为100Ωm、层厚度为1000m;第二层为连续介质层,介质电阻率随深度线性减小,其变化关系如图中所示,层厚度为1000m;第三层电阻率为1Ωm;测点区域为0~4km,点距为100m,共41个测点,频率范围为103~10-3Hz,以10为底的对数间隔采样,共51个频点.
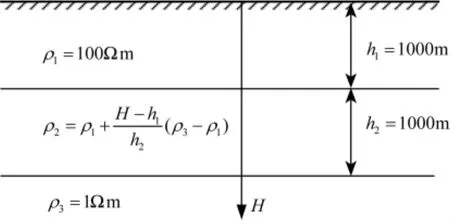
图4 三层地电断面模型Fig.4 Schematic diagram for geoelectric section of model 3 layers
在一维层状介质的解析法中,将中间的连续介质层剖分为10层进行模拟.在二维有限元数值模拟中,取测线中心处第21号点测点为研究对象.则解析法与二维数值解法的结果对比如图5所示.
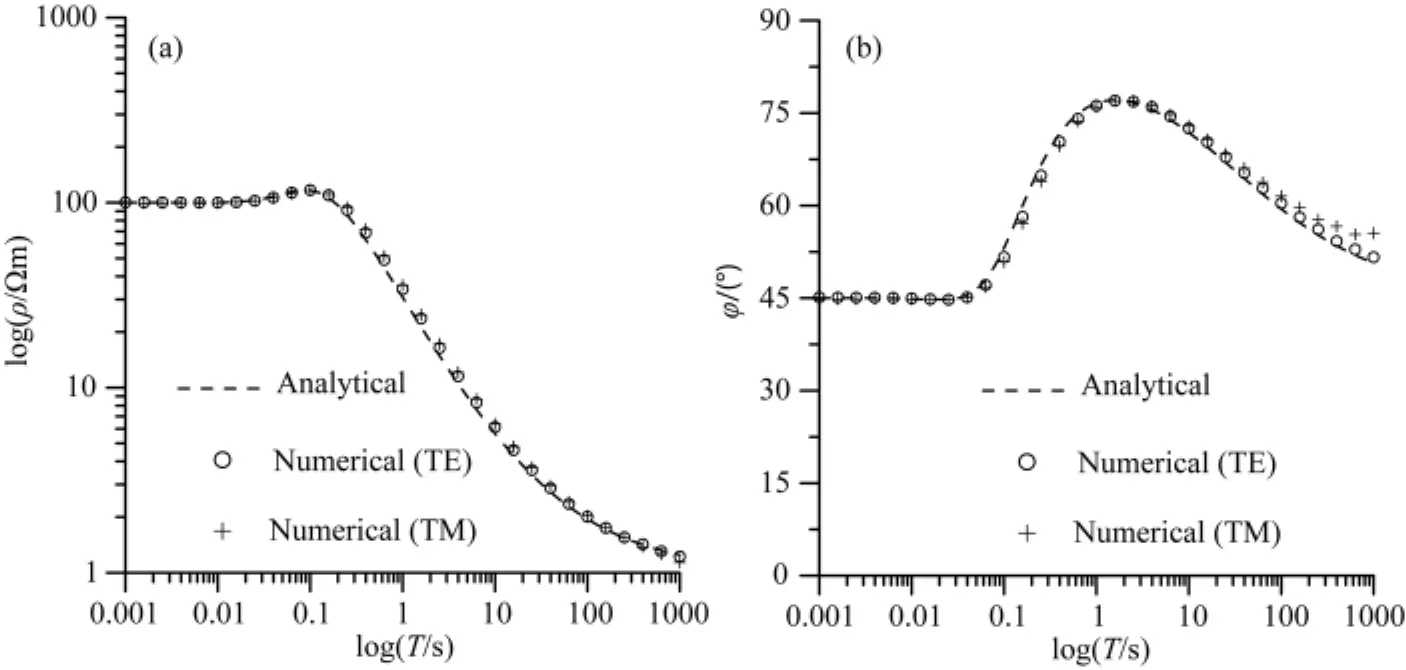
图5 有限元数值解与解析法结果比较Fig.5 Comparison between analytical and numerical solutions by FEM
在TE、TM视电阻率曲线图和阻抗相位曲线图上,解析法和数值解曲线形态、值的大小基本一致,这表明本文方法能够有效地模拟连续介质模型.正演结果的数据统计表明,视电阻率、阻抗相位的解析法结果和数值模拟结果均方根误差均小于1%.本文的数值模拟结果与解析法结果之间的误差分析主要为:一方面,与有限元数值模拟的网格剖分有关系,如高频网格和低频网格的剖分方式是不一样的;另一方面,解析法是基于电性参数分层均匀的计算方式,而本文的数值模拟方法是基于电性参数分块连续变化的模拟.
5.2 地形模型
如图6下部所示为圆柱凹陷地形模型,Wanna maker等[1]和徐世浙等[20]在文献中对这个模型做过模拟.测点区域为0~0.4km,点距为10m,共41个测点,圆半径为50m,频率为0.01Hz,计算TM模式下视电阻率.
本文数值模拟结果如图6上部曲线图所示,对照文献[1,20]中模拟结果,在0.01Hz频点处,TM模式下,三种模拟方法与地形测点对应的视电阻率起伏形态和值的大小基本一致.
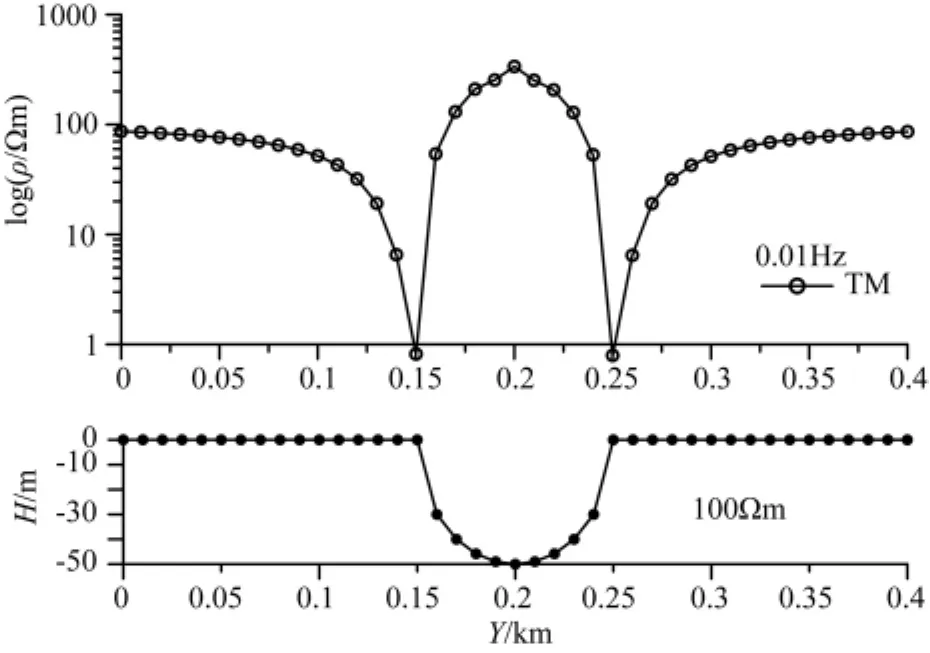
图6 圆柱凹陷地形模型与TM模式计算结果Fig.6 Topography of columnar sunken model and Result of TM
图7所示为山脊地形模型,在文献[1,20]中对这个模型做过模拟.测点区域为0~4km,点距为50m,共81个测点,起伏落差为100m,山底宽度为2.4km,频率为10Hz.
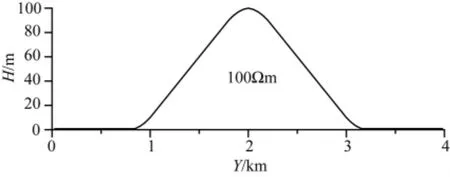
图7 山脊地形模型Fig.7 Chine terrain model
本文数值模拟结果如图8所示.对照文献[1,20]中的模拟结果,在10Hz频点处,TE、TM模式下,三种模拟方法与地形测点对应的视电阻率、阻抗相位起伏形态和值的大小基本一致.
通过对以上两例均匀大地起伏地形模型的模拟,得到了与前人研究相符的结论.分块均匀法认为地面或地下单元内节点之间的电性参数是均匀分布的,而本文的分块连续法则认为地面或地下单元内节点之间的电性参数是连续变化的(空气介质除外).显然,分块均匀法是分块连续法的特殊形表现形式,分块连续法更具有普遍性.用三角网格模拟起伏地形、分块连续变化的剖分方式且更加符合野外实际地质情况.
5.3 倾斜界面异常体模型
如图9所示为“W”字形倾斜界面异常体模型,背景电阻率为100Ωm,异常体电阻率为20Ωm,其上顶面距地面100m,下底面距地面500m,异常体上顶面外宽4800m,下底面外宽2400m.测点区域为0~8km,点距为100m,共81个测点,频率为103~10-1Hz,以10为底的对数间隔采样,共41个频点.
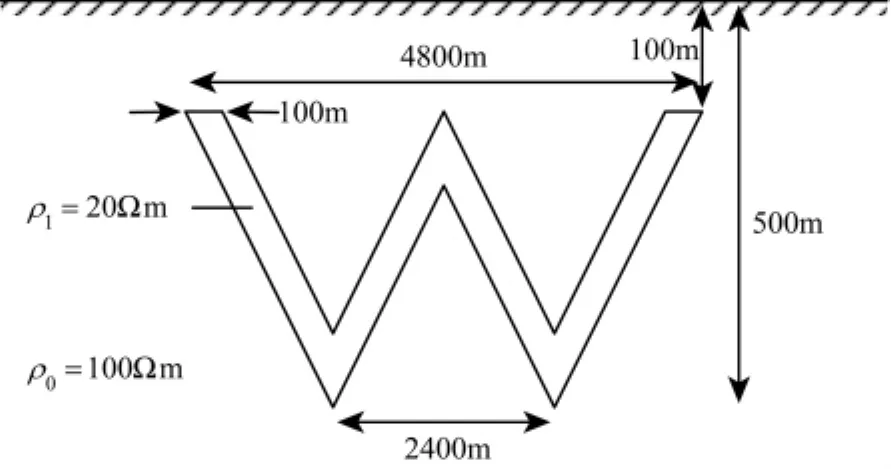
图9 倾斜界面异常体模型Fig.9 Model of slopeing interface abnormity body
有限元数值模拟网格剖分为:最大探测深度选择为10km,等比网格系数选择为1.1;TE模式,网格数为116×66(横向网格数为116,左、右稀疏网格数各为18;纵向网格数为66,其中包括空气稀疏网格数为14);TM模式,网格数为116×52(横向网格数同TE模式;纵向网格数为52,没有空气网格).大型稀疏矩阵的存储方式均按文献[13,15]中变带宽方式存储,用不带平方根的Cholesky分解法求解线性方程组[13,16].
本文数值模拟方法的结果剖面图如图10所示,计算每一个频点的时间为0.78s(TE和TM模式同时计算).在TE、TM两种极化模式下,视电阻率、阻抗相位剖面上都出现明显低阻异常,“W”形异常形态清晰可见,表明采用三角网格模拟任意倾斜界面异常体的方法是有效的.
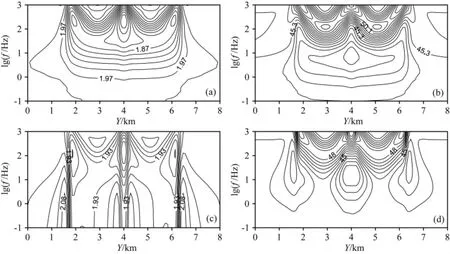
图10 (a)TE视电阻率剖面(单位:Ωm);(b)TE阻抗相位剖面(单位(°));(c)TM视电阻率剖面(单位:Ωm);(d)TM阻抗相位剖面(单位(°))Fig.10 TE profile of apparent resistivity(a);TE profile of impedance phase(b);TM profile of apparent resistivity(c);TM profile of impedance phase(d)
6 结 论
本文提出三角单元网格剖分、电性参数分块连续变化二维MT有限元数值模拟方法,比较矩形单元剖分、电性参数分块均匀的模拟方法,这样既不增加节点,节省了计算时间,又能很好模拟野外实际地形和任意地电体模型.通过对一维连续介质模型模拟计算,与解析法计算结果对比,验证了本文算法的可靠性;对前人地形模型模拟计算,结果与前人结果相符;对任意倾斜界面异常体模型进行模拟,结果表明本方法是有效的.同时指出,本方法仍然是考虑各向同性介质情况,对各向异性介质分块连续变化的数值模拟方法将是本文的后续研究工作.
致 谢 在本文程序的编制、有限元网格剖分方法以及辅助场的计算中,陈小斌研究员和作者进行多次坦诚交流和讨论,并提出许多宝贵意见,谨在此表示衷心感谢.
(References)
[1] Wanna maker P E,Stodt J A,Rijofi L.Two-dimensional topographic responses in magnetotellurics modeled using finite elements.Geophys.,1986,51(11):2131-2144.
[2] Mauriello P,Patella D.Principles of probability tomography for natural-source electromagnetic induction fields.Geophys.,1999,64(5):1403-1417.
[3] 陈小斌,张翔,胡文宝.有限元直接迭代算法在MT二维正演计算中的应用.石油地球物理勘探,2000,35(4):487-496.Chen X B,Zhang X,Hu W B.Application of finiteelementdirect iteration algorithm to MT 2-D forward computation.Oil Geophysical Prospecting (in Chinese),2000,35(4):487-496.
[4] 陈小斌.MT二维正演计算中地形影响的研究.石油物探,2000,39(3):112-120.Chen X B.On the research of the influence of terrain to MT 2D forward computation.Geophysical Prospecting for Petroleum (in Chinese),2000,39(3):112-120.
[5] 谢飞.带地形大地电磁场二维有限元数值模拟研究.北京:中国地质大学,2006.Xie F. Two-dimension Topographic Numeric Simulation Research in Magnetotellurics Using Finite Elements(in Chinese).Beijing:China University of Geosciences,2006.
[6] 周熙襄,钟本善.电法勘探数值模拟技术.成都:四川科学技术出版社,1986.Zhou X X,Zhong B S,et al.Numerical Modeling for Electrical Exploration (in Chinese).Chengdu:Sichuan Science and Technology Press,1986.
[7] 王绪本,李永年,高永才.大地电磁测深二维地形影响及其校正方法研究.物探化探计算技术,1999,21(4):328-332.Wang X B,Gao Y N,Gao Y C.Two dimentional topographic responses in magneto telluric sounding and its correction methods.Computing Techniques for Geophysical and Geochemical Exploration (in Chinese),1999,21(4):328-332.
[8] 刘云,王绪本.大地电磁二维自适应地形有限元正演模拟.地震地质,2010,32(3):382-391.Liu Y,Wang X B.FEM using adaptive topography in 2DMT forward modeling.Seismology and Geology (in Chinese),2010,32(3):382-391.
[9] 徐世浙,于涛,李予国等.电导率分块连续变化的二维MT有限元模拟(Ⅰ).高校地质学报,1995,1(2):65-73.Xu S Z,Yu T,Li Y G,et al.The finite element method for modeling 2-D MT field on a geoelectrical model with continuous variation of conductivity within each block.Geological Journal of Universities (in Chinese),1995,1(2):65-73.
[10] 李予国,徐世浙,刘斌等.电导率分块连续变化的二维MT有限元模拟(Ⅱ).高校地质学报,1996,2(4):448-452.Li Y G,Xu S Z,Liu B,et al.The finite element method for modeling 2-D MT field on a geoelectrical model with continuous variation of conductivity within each block.Geological Journal of Universities (in Chinese),1996,2(4):448-452.
[11] 朴化荣.电磁测深法原理.北京:地质出版社,1990.Piao H R.Theory of Electro magnetics(in Chinese).Beijing:Geology Press,1990.
[12] 曾国.大地电磁二维有限元正演数值模拟.湖南:中南大学,2008.Zeng G.FEM in 2-D Forward Modeling (in Chinese).Hunan:Central South University,2008.
[13] 徐世浙.地球物理中的有限单元法.北京:科学出版社,1994.Xu S Z.FEM in Geophysics(in Chinese).Beijing:Science Press,1994.
[14] 阮百尧.三角单元部分电导率分块连续变化点源二维电场有限元数值模拟.广西科学,2001,8(1):1-3.Ruan B Y.2-D electrical modeling due to a current point by FEM with variation of conductivity within each triangular element.Guangxi Sciences(in Chinese),2001,8(1):1-3.
[15] 阮百尧,熊 彬.大型对称变带宽方程组的Cholesky分解法.物探化探计算技术,2000,22(4):361-368.Ruan B Y,Xiong B.A cholesky decomposition method for large-scale symmetrical system of equations with varying band-width.Computing Techniques for Geophysical and Geochemical Exploration (in Chinese),2000,22(4):361-368.
[16] 刘德贵,费景高,于泳江等.FORTRAN算法汇编(第一分册).北京:国防工业出版社,1980.Liu D G,Fei J G,Yu Y J,et al.FORTRAN Algorithm Collection (Volume 1) (in Chinese).Beijing:National Defense Industry Press,1980.
[17] 马为.MT二维正演中辅助场计算新方法研究.北京:中国地震局,2007.Ma W.A Study of New Algorithm for the Calculation of Auxiliary Field in MT 2D Forward Modeling (in Chinese).Beijing:China Earthquake,2007.
[18] 马为,陈小斌,赵国泽.大地电磁测深二维正演中辅助场的新算法.地震地质,2008,30(2):525-533.Ma W,Chen X B,Zhao G Z.A new algorithm for the calculation of auxiliary field in MT 2D forward modeling.Seismology and Geology (in Chinese),2008,30(2):525-533.
[19] 史明娟,徐世浙,刘斌.大地电磁二次函数插值的有限元法正演模拟.地球物理学报,1997,40(3):421-430.Shi M J,Xu S Z,Liu B.Finite element method using quadratic element in MT forward modeling.Chinese J.Geophys.(in Chinese),1997,40(3):421-430.
[20] 徐世浙,王庆乙,王军.用边界单元法模拟二维地形对大地电磁场的影响.地球物理学报,1992,35(3):380-388.Xu S Z,Wang Q Y,Wang J.Modeling 2-D terrain effect on MT by the boundary element method.Chinese J.Geophys.(in Chinese),1992,35(3):380-388.
The FEM for modeling 2-D MT with continuous variation of electric parameters within each block
LIU Yun,WANG Xu-Ben*
State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation,Chengdu University of Technology,Chengdu610059,China
To model arbitrarily shaped two-dimensional topography and structures in field work,triangular element grid was used in the finite element method (FEM).In view of the fact of continuous variation of the subterranean rock-mineral electric parameters,the electromagnetic field and some electric parameters of models are designed to bilinear variation within each triangular element in our numeric modeling method,and which is developed for modeling two dimensional magnetotelluric (MT)under the field topography condition.The calculation for mulae of the auxiliary field,and the definition of apparent resistivity and impedance phase are deduced according to the relationship between the main fields of the three nodes and the linear shape function within each element.By calculating a continuous medium model and two topography models set up by other scholars to test our method,the result of our method shows a high accuracy (the mean square error is less than 1%),and the results of modeling two topography models accord with other scholar′s,too.Through modeling a sloping interface abnormity body,we find that our method can model arbitrarily complicated terrain and geoelectric bodies preferably.
MT,Topography,Triangle grids,Continuous variation of electric parameters within each block,FEM
10.6038/j.issn.0001-5733.2012.06.029
P631
2011-06-17,2012-05-08收修定稿
国家高技术研究发展计划重点项目子课题(2009AA06Z108)资助.
刘云,男,1973年生,博士研究生,主要从事电磁场数值模拟及反演成像技术研究.E-mail:liuyun0077@163.com
*通讯作者 王绪本,男,教授、博士生导师,主要从事电磁场数值模拟及反演成像技术研究.E-mail:wxb5501@yahoo.com.cn
刘云,王绪本.电性参数分块连续变化二维 MT有限元数值模拟.地球物理学报,2012,55(6):2079-2086,
10.6038/j.issn.0001-5733.2012.06.029.
Liu Y,Wang X B.The FEM for modeling 2-D MT with continuous variation of electric parameters within each block.Chinese J.Geophys.(in Chinese),2012,55(6):2079-2086,doi:10.6038/j.issn.0001-5733.2012.06.029.
(本文编辑 汪海英)
