3维干旱变量联合概率分布研究

晁智龙

(陕西省水文水资源勘测局，陕西 西安710068)

干旱一般是指长期少降水或无降水的现象，一般分为气象干旱、农业干旱、水文干旱和社会经济干旱 。由于干旱的特性是随机的，因此，概率方法成为描述干旱特性的重要方法之一。继Yevjevich(1967)提出游程理论以来，单变量干旱特性(干旱历时、干旱烈度、干旱强度和到达间隔)概率分布研究取得了显著的成果。与其他水文变量一样，单变量干旱特性一般被认为是独立的、同分布的。然而，干旱特征一般表现为多个相依变量组成的复杂水文事件，单变量只是描述干旱的一种特征属性，无法全面反映干旱事件的真实特征。20世纪90年代以来，多变量的联合分析成为水文分析的研究热点。但是，多变量联合分布要求各变量的边际分布属于同一类型分布，而实际的水文变量可能服从不同类型的分布;随着分析变量数的增加，需要较多的数据，数学模型复杂，求解困难。一些学者采用两变量正态分布、指数分布、Gamma分布和极值分布描述多变量的联合分布［1-13］。近年来，Copula函数被引入多变量联合分布分析，克服上述多变量联合分布构建的缺点，被广泛地应用于洪水、暴雨等极值水文事件的联合概率分布分析，成为水文计算领域的一个研究热点，研究表明，Copula函数能有效地描述水文事件的内在规律和反映特征属性之间的相互关系［3］。目前，采用3维变量copula函数研究干旱特性较少，多变量的频率分析大多采用两变量Copula函数进行推求联合分布。本文在吸收国外Copula函数研究成果的基础上，以渭河流域北洛河状头站的径流序列为例，采用游程理论选择干旱历时、干旱烈度和烈度峰值为水文干旱特性变量(以下简称干旱变量)，应用3维Archimedean copula研究单变量分布的拟合度检验、相依变量的度量、Copula函数的拟合度检验以及干旱变量的联合概率分布，通过数学推导，给出了3维条件概率和重现期的计算公式，阐述3维ArchimedeanCopula函数研究干旱特性联合分布的方法。文中方法同样适用于其他水文变量的联合分布计算。

1 干旱定义

根据游程理论，一个干旱事件是指在一定时间段内，径流小于或等于截取水平值。本文选择干旱历时(D)、干旱烈度(S)和烈度峰值(P)来描述干旱事件。截取水平值(Threshold level)选取年径流或月径流序列(t=1，2，…，12)的均值。干旱历时即负游程长度，指径流连续低于截取水平值的年或月份数。干旱烈度为干旱事件在干旱历时内低于截取水平值的亏缺水量和，也称负游程总量。烈度峰值表示干旱事件在干旱历时内的最大亏缺水量。

2 3维Archimedean copulas

Copula的定义和性质可参见有关文献，这里不再叙述。对于1个参数的Archimedean Copula函数，Copula可以表示为

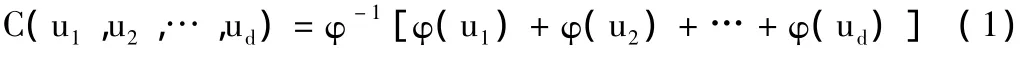
式中，φ(t)称为Archimedean Copula的生成函数(generator function)，它完全决定了Archimedean Copula的形式。

3 应用实例

本文选用渭河流域北洛河状头站(1937-2006年)的月径流序列，截取水平取各月的平均流量值。

3.1 边际分布和参数计算

干旱变量的经验分布采用Gringorten position-plotting formula公式计算。干旱历时假定服从2参数Weibull分布，干旱烈度和烈度峰值服从2参数Gamma分布。采用矩法(MOM)、极大似然法(MLM)，概率权重法 (PWM)和遗传算法(GA)进行参数估计(见表2)。根据均方根误差(Root Mean Square Error—RMSE)，Akaike信息准则 (Akaike Ⅰnformation Criteria—AⅠC)和 Bayesian信息准则 (Bayesian Ⅰnformation Criteria—BⅠC)进行最优参数选择。经计算，GA法对应的AⅠC、BⅠC和RMSE值均为最小，所以，3种干旱变量的边际分布参数选择GA法估算的参数。

干旱历时采用χ2检验。干旱烈度和烈度峰值分别采用Kolmogorov-Smirnov(K—S)检验 Dn、Cramer-von Mises(C—M)检验、Aderson-Darling(A—D)检验、修正权重Watson检验和 Liao—Shimokawa检验 Ln［6，24］。取模拟样本数NB=3000，5种样本统计检验值均小于相应的检验临界值;所以，本文接受干旱烈度和烈度峰值服从 2参数Gamma分布。

3.2 变量相依性的度量与Copula参数计算

采用Pearson’s古典相关系数 γ，Spearman秩相关系数ρ，Kendall’sτ，Chi-Plots，and K-Plots进行干旱变量相依性的度量［25］。γ、ρ 和 Kendall’sτ均大于 0.5，表明了干旱历时、干旱烈度和烈度峰值间有较强的相依性。

3维干旱变量的联合经验分布仍采用Gringorten position-plotting公式计算。对于3维Archimedean Copula，采用极大似然法进行参数估算。似然函数两边取对数，求θ的导数，并令其导数表达式等于0，有:

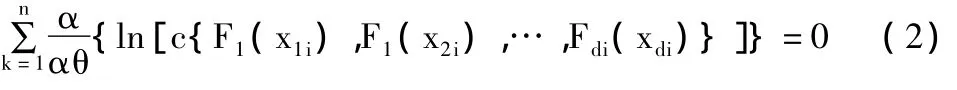
根据 Gumbel Copula、Frank Copula、Clayton Copula 和 Ali-Mikhail-Haq Copula参数的取值范围，本文采用二分法求解式(2)所示的非线性方程组，见表1。

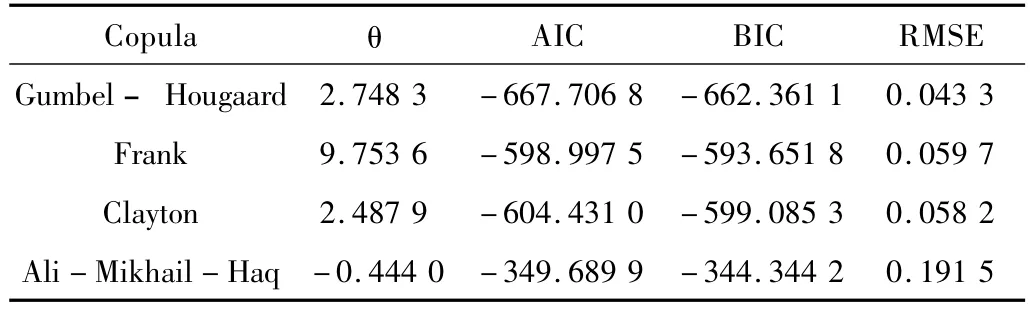
表1 三变量Archimedean copulas联合分布参数和拟合评价计算结果

表1表明 Gumbel Copula的 AⅠC、BⅠC和 RMSE值最小。因此，本文选用3维Gumbel Copula描述干旱变量的联合分布特性。

3.3 条件概率和重现期计算

干旱变量是按照截取水平获得的，这实际上是一个部分历时序列(Partial duration series，PDS)，对于给定的截取水平(Threshold level)，边际分布为FX(x)的重现期TX应按下式进行计算。

对于2维联合分布 F(X≤x，Y≤y)=C(u1，u2)和条件分布 F1(X≤x|Y=y)，F2(Y≤y|X≤x)，边际分布 u1=FX(x)，u2=FY(y)，2维重现期T(X≤x，Y≤y)和条件重现期 T(X≤x|Y=y)、T(X≤x|Y≤y)计算为:

3维重现期T(X≤x，Y≤y，Z≤z)和条件重现期T(X≤x|Y=y，Z=z)、T(X≤x，Y≤y|Z=z)、T(X≤x|Y≤y，Z≤z)有类似计算式，本文不再列举。

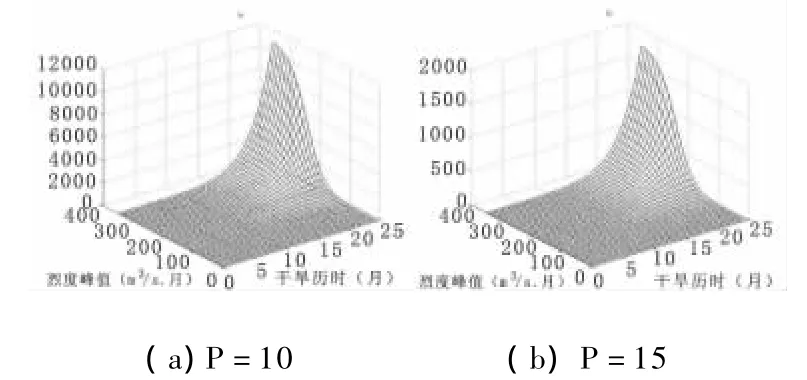
图1 给定P=p条件，D≤d，V≤v出现的重现期

所以，上式条件重现期关键在于如何计算相应的条件概率。由概率论原理，我们可以推导出这些条件概率的计算公式。

图1分别给出了在P=10、P=15条件下，(D≤d，V≤v)事件发生的重现期。

4 结语

本文以干旱变量联合分布为例，在吸收当前copula函数研究成果的基础上，系统地阐述了单变量分布的拟合度检验，相依变量度量，copula参数估算，最优 copula选择以及copula拟合度检验等方法和步骤。上述这些问题均为copula函数在多变量水文频率分析中的几个关键技术问题。最后，通过数学推导，给出了多变量条件概率计算以及相应的重现期计算公式，更正了Zhang L，Singh VP(2007)给出给定两变量值(X=x，Y=y)条件下，事件Z≤z发生的条件概率计算公式。采用截取水平获得的水文序列实际上是一个部分历时序列(PDS)，其重现期应采用Kim(2003)给出的公式进行计算。文中实例应用表明:copula函数能够推求变量不同组合条件下的概率分布，是推求干旱多变量联合分布和其他水文多变量联合分布的有效途径，文中方法同样适用其它水文变量的联合分布计算。

［1］袁超，宋松柏，荆萍.极限水文干旱历时概率分布解析法研究［J］.西北农林科技大学学报(自然科学版).2008，36(7):212-218.

［2］郭生练，闫宝伟，肖义，等.Copula函数在多变量水文分析计算中的应用及研究进展［J］.水文.2008，38(3):1-7.

［3］熊立华，郭生练，肖义，等.Copula联结函数在多变量水文频率分析中的应用［J］.武汉大学学报(工学版).2005，38(6):16-19.

［4］冯平，毛慧慧，王勇.多变量情况下的水文频率分析方法及其应用［J］.水利学报.2009，40(1):33-37.

［5］许月萍，李佳，曹飞凤，等.Copula在水文极限事件分析中的应用［J］.浙江大学学报(工学版).2008.