BP神经网络PID控制在稀土永磁无刷直流电动机伺服系统中的应用

刘 伟 ,周俊敏 ,李景红

(1.周口师范学院物理与电子工程系,河南周口466001;2.河南济源供电公司,河南济源454650)

稀土永磁无刷直流电动机是一种比较典型的机电一体化产品,具有体积小、质量轻、效率高、转动惯量小和响应快等特点,同时还保留有直流电动机优良的控制特性。电动机的转子上粘有已充磁的永磁体,目前采用的永磁材料主要是铁淦氧、铝镍钴、钕铁硼等合金,应用最为广泛的为钕铁硼(Nd-Fe-B)。它的磁感应强度和磁场强度线性关系范围最大,被称为第三代稀土永磁合金。为检测电动转子的极性,在电动机内装有位置传感器。驱动器由功率电子器件和集成电路等构成。无刷直流电机具有低电压特性好、转矩过载能力强、堵转特性好、启动电流小等优点。由于无刷直流电动机是以自控式运行的,所以不会像变频调速下重载启动的同步电机那样在转子上另加启动绕组,也不会在负载突变时产生振荡和失步。本文介绍一种基于BP算法的PID控制算法,针对某直线伺服作动系统,采用稀土永磁无刷直流电动机,并对此系统在MATLAB平台上进行了仿真[1]。

1 系统的结构及数学模型

永磁无刷直流电动机是由无刷直流电动机本体、转子位置传感器和驱动控制器组成的机电一体化系统。图1中的位置检测是BLDCM特有的转子位置信号,用于电机功率电子换向。该电机具有普通直流电机优良的机械特性,其单通道转速、电流双闭环控制系统结构如图1所示。

一般,无刷直流电动机的动态方程为:

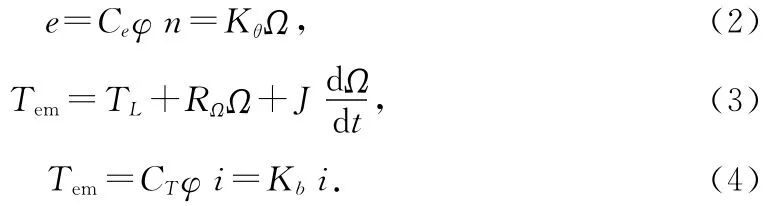
式中u,ia,e,Tem分别为电机动态过程中的电压(V)、电流(A)、感应电动势(V)、电磁转矩(N.m)的瞬时值;La为电枢电感(H);Ra为电枢电阻(Ω);Tem为负载转矩,包括电动机轴上输出转矩和恒定阻力转矩(N.m);TL为输出转矩(N.m);Kθ为转矩系数;RΩ为阻力系数;Ω为转子机械角速度(rad/s);J为转子转动惯量(kg.m2);n为转子瞬时转速(r/min)。对式(1)～(4)进行拉普拉斯变换,并且转化为另一种数学模型——方框图,如图2所示。

2 基于BP神经网络的PID整定原理

2.1 算法原理

基于BP(Back Propagation)神经网络的PID控制器由两部分组成:

1 )传统的PID控制器。直接对被控对象进行闭环控制,并且在线调整三个参数kp、ki、kd。

2 )神经网络。根据系统的运行状态,调节PID控制器的三个参数,使其达到某种性能指标的最优化。即使输出层神经元的输出状态对应于PID控制器的三个可调参数kp、ki、kd,通过神经网络本身的自学习、加权系数自调整,从而使其稳定状态对应于某种最优控制规律下的PID的控制器参数。基于BP神经网络自整定PID控制系统方框图如图3所示[2,3]。

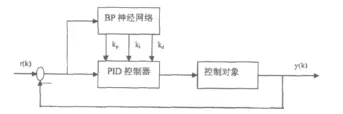
图3 基于BP神经网络自整定PID控制系统原理图

2.2 基于BP网络的PID控制器控制的算法流程

基于BP网络的PID控制器控制算法可归纳如下[4,5]:

1 )确定BP神经网络的结构包括输入层节点数M及隐含层数目Q,并给出各层权系数的初值w(0)和w(0)、选定学习率η、惯性系数α;

2 )采样得到r(k)、y(k),计算该时刻误差e(k)=r(k)-y(k);

3 )计算神经网络各层神经元的输入、输出,其输出层的输出即为PID控制器的三个可调参数kp、ki、kd;

4 )计算PID控制器的输出u(k);

6 )置k=k+1,返回到第一步。

2.3 基于BP神经网络的PID控制MATLAB仿真

控制器中的加权系数采用BP神经网络学习算法进行自整定,加权系数初始矩阵区间为[-0.5,0.5]。按照上面的算法用MATLAB编程,仿真直流伺服电机位置控制如图4、图5、图6所示。

图4 BP神经PID控制下的个参数变化曲线

3 结语

从以上仿真结果分析,基于BP神经网络的自整定PID控制能依据被控对象的情况自适应地调整PID的三个参数,依据一定的最优准则以求满足不同负荷下的控制要求。实现了基于BP神经网络的PID控制算法,并用于直流伺服电机调速的实际中。结果表明:采用BP神经网络的PID控制系统具有超调量小、调节速度快、准确率高等特点,得到了较理想的控制效果。

[1]刘金琨.智能控制[M].北京:电子工业出版社,2005: 185-187.

[2]程启明,陈刚,王勇浩.电厂过热汽温神经PID控制系统的仿真研究[J].上海电力学院学报,2005,21(2): 38-41.

[3]王新亚.基于MEA-BP神经网络的主汽温控制系统的研究[J].山西焦煤科技,2009(3):13-15.

[4]王亚斌.基于BP神经网络PID控制及其仿真[J].江苏冶金,2008,36(2):33-25.

[5]薛阳,叶建华,钱虹,等.火电机组过热汽温神经网络控制的研究[J].上海电力学院学报,2009,25(1):33-38.