复合管柱初始压缩量计算分析

侯兴华，杨 辉，薛世峰，朱秀星

（中国石油大学（华东）储运与建筑工程学院，山东青岛266555） ＊

复合管柱初始压缩量计算分析

侯兴华，杨 辉，薛世峰，朱秀星

（中国石油大学（华东）储运与建筑工程学院，山东青岛266555）＊

复合管柱在油气井封隔器完井工艺中应用广泛，由于其结构复杂，初始压缩量的计算不能单纯地采用单一管柱的计算方法。针对三级复合管柱，分析了坐封后中和点的位置，并依据此位置分4种情况推导了管柱初始压缩量的计算公式。以某油井复合管柱结构为例，计算了井筒流体作用下管柱的初始压缩量，为现场施工提供参考。

复合管柱；初始压缩量；封隔器；中和点

1 问题的提出

复合管柱在油田生产过程中应用广泛，但目前初始压缩量的计算方法未考虑管柱结构影响及变形后作用力作用方式的改变等因素的影响，误差较大，使得施工人员很难获得准确的管柱初始压缩量，导致重复施工甚至坐封失败，带来巨大的经济损失。

目前，对管柱初始形变的分析多数运用鲁宾斯基经典方法［1］，忽视了管柱变形后作用力作用方式的变化。李钦道［2］等人对单一管柱初始压缩量进行了研究，但由于复合管柱结构的复杂性，不能单纯地运用单一管柱初始压缩量的计算方法。本文针对复合管柱结构特点，在力学分析的基础上建立了更为准确的初始压缩量计算公式。

2 复合管柱初始压缩量的计算

基本假设条件：①油管和套管为2种尺寸；②每一级管柱都有足够的长度，忽略2级之间对弯曲的影响；③井内充满液体；④不考虑油管与套管之间的摩擦。

现有1根三级复合油管柱悬挂在有流体的井中，根据油管柱的管径把管柱分为2段。坐封前的管柱形态如图1所示。

坐封前的油管在流体作用力和自重作用下产生变形。将坐封后的管柱划分为2段进行计算，即弯曲段和直线段。初始管柱压缩量等于坐封后的变形减去坐封前的变形。由于各段油管自重引起的变形在坐封前后都存在且不变，本文中计算不再考虑［3］。

图1 坐封前的管柱形态

2.1 管柱坐封前的变形

坐封前，管柱全部处于直线状态，则第1段底部（封隔器处）的实际力（活塞力）（压缩为正，拉伸为负，下同）为［1］

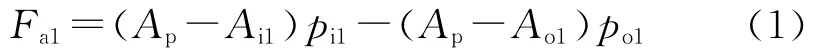
式中，Fa1为第1段管柱底部的实际力，N；Ap为封隔器密封腔孔的面积，mm2；Ai1为第1段油管的内面积（以内径算），mm2；Ao1为第1段油管的外面积（以外径算），mm2；pi1为封隔器处油管内压，Pa；po1为封隔器处油套环形空间压力，Pa。

由于在初始状态下油管内外压力相等，令

将式（2）代入式（1），得

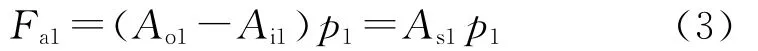
式中，As1为第1段管柱横截面积，mm2。

第2段底部（如图1中的第3级底部）的实际力（不再考虑第1段油管重力）为

式中，Fa2为第2段管柱底部的实际力，N；F′a1等于式（3）计算出的Fa1，N；F′a2为油管肩部受液压产生的作用力，N；Ai2为第2段油管的内面积（以内径算），mm2；Ao2为第2段油管的外面积（以外径算），mm2；pi2为第2段油管底部内压，Pa；po2为第2段油管底部环形空间压力，Pa。

同理可令

将式（3）、（5）、（6）代入式（4），得

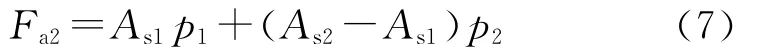
式中，As2为第2段管柱横截面积，mm2。

根据虎克定律［4］，坐封前整个管柱的变形（缩短为正，伸长为负，下同）为

式中，ΔLq为坐封前的管柱变形量，m；ΔL1为坐封前的第1段管柱变形量，m；ΔL2为坐封前的第2段管柱变形量，m；L1为第1段油管的长度，m；L2为第2段油管的长度；E为钢材的弹性模量，N／m2。

将式（3）和式（7）代入式（8），得

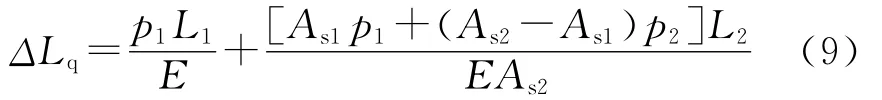
2.2 管柱坐封后的形变

坐封后管柱会发生弯曲，由于内外压相等，则“虚构力”等于零，此时管柱在封隔器处只受到封隔器的作用力［5－8］。

2.2.1 中和点位置的确定

假设中和点在第1段管柱上，则中和点距管柱底部的长度为［9］

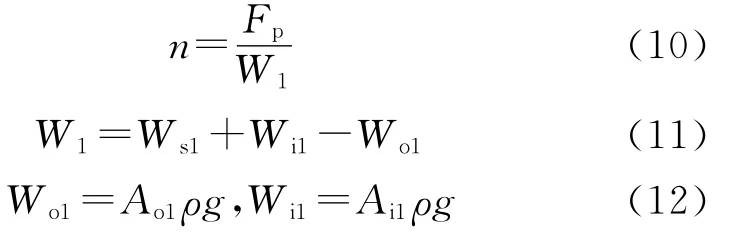
式中，n为中和点距油管底部的长度，m；Fp为第1段油管底部的压缩力，即坐封时井口释放的油管重力，N；ρ为井中流体的密度，kg／m3；W1为第1段油管单位长度在流体中的重力，N／m；Ws1为第1段油管单位长度在空气中的重力，N／m；Wi1为第1段单位长度油管内流体的重力，N／m；Wo1为第1段单位长度油管体积（以外径计算）排开套管内流体的重力，N／m；g为重力加速度，m／s2。

将式（12）代入式（11），得

若n值小于第1级油管的长度L′1，则中和点在第1级管段（如图2a）；若n值大于第1级管段长度而小于第1级L′1和第2级管段长度L′2之和（L′1＜n＜L′1＋L′2，L′1＋L′2＝L1），则中和点在第2级管段（如图2b）；若n值大于第1级和第2级管段长度之和（n＞L1），此时可用式（14）进行第2段（第3级）的计算，即

式中，W2为第2段管柱单位长度在流体中的重力，N／m；Ws2为第2段单位长度管柱在空气中的重力，N／m。

若n＜L1＋L2，则中和点在第3级管段（如图2c），否则中和点在管柱外（如图2d），管柱处于全部弯曲状态。

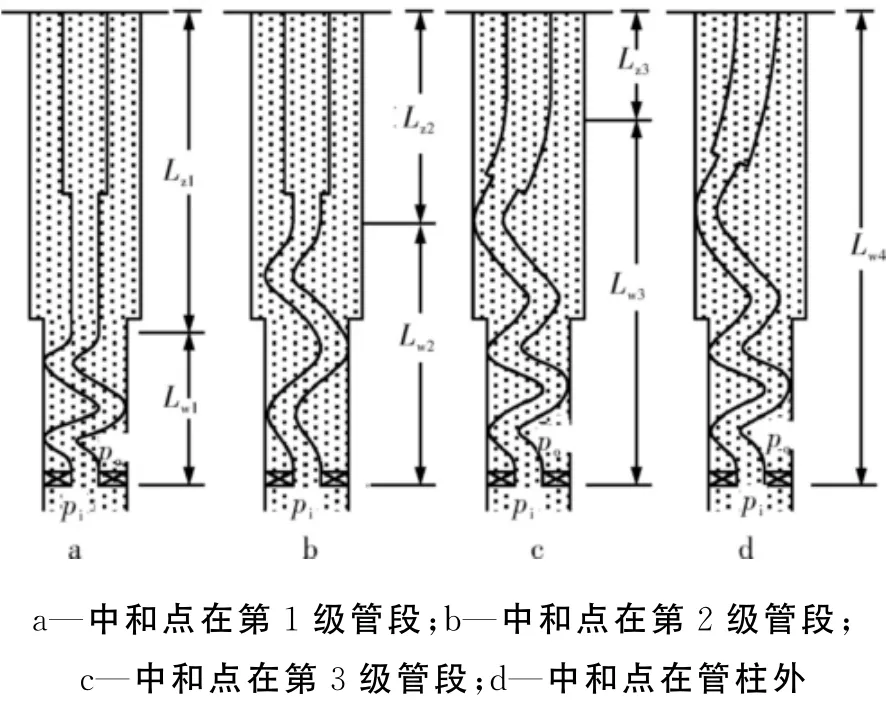
图2 坐封后不同中和点位置时的管柱形变

2.2.2 坐封后弯曲段的变形

坐封后管柱发生弯曲，流体在竖直方向上的作用力演变为沿长度均匀分布的分散力。因此，油管弯曲段的变形包括3个部分，即封隔器对油管的作用力引起的变形、沿长度线性分布的浮力引起的变形和螺旋弯曲引起的变形［9］。

1） 封隔器对油管的作用力引起的变形。

根据虎克定律［4］，封隔器对油管的作用力引起的变形为

式中，ΔLp为封隔器对油管作用力引起的变形，m；F′p为各级管柱底部受封隔器的作用力，N；Lw为弯曲管段长度，m；As为油管管壁的横截面积，mm2。

根据中和点的位置，分别代入相应的F′p、Lw和As值。

①第1种情况（如图2a）。

②第2种情况（如图2b）。

③第3种情况（如图2c）。

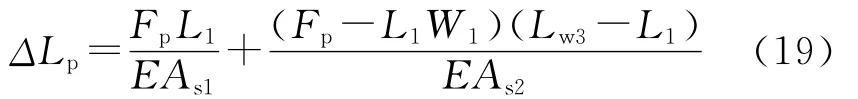
④第4种情况（如图2d）。

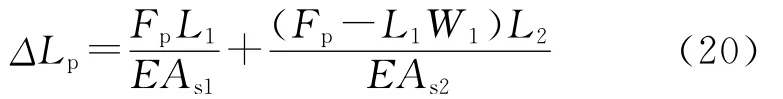
2） 沿线性分布的浮力引起的变形。

根据工程流体力学，单位长度油管受到的浮力为Wo－Wi。下面就中和点位置的不同分为4种情况给出浮力引起的变形［10］。

①第1种情况。

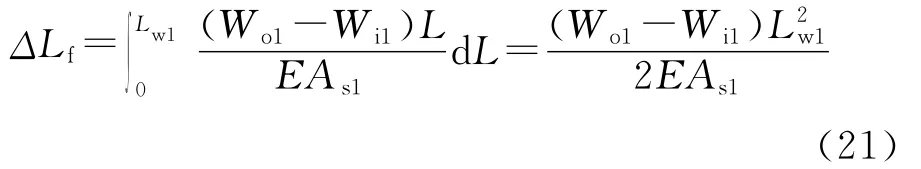
式中，ΔLf为浮力引起的变形，m；Wo为单位长度油管受到的管外流体作用力，N／m；Wi为单位长度油管内流体的重力，N／m。

将式（12）代入式（21）可得

②第2种情况。

③第3种情况。

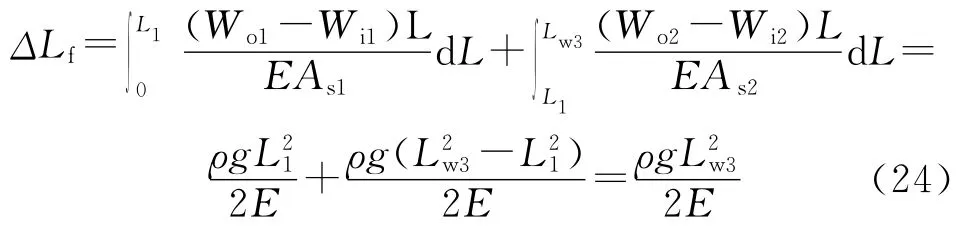
④第4种情况。

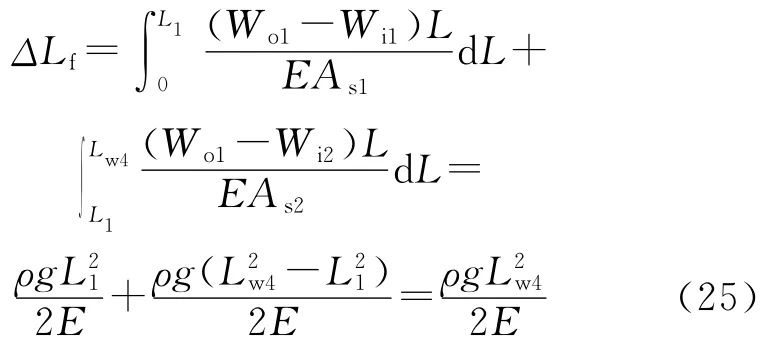
在式（17）～（25）中，弯曲段长度等于中和点距油管底部的距离n。

3） 螺旋弯曲引起的变形。

管柱弯曲后会发生螺旋弯曲变形。中和点以下的全部管柱都是弯曲的，而中和点所在的那一级管柱只有部分弯曲。对于完全弯曲的管柱都可以用式（26）确定［11］，即

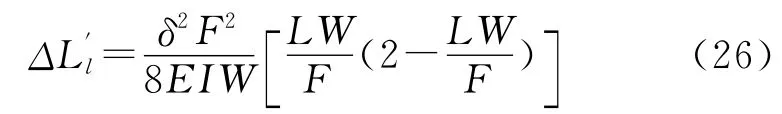
式中，ΔL′l为完全弯曲的管柱因螺旋弯曲引起的变形，m；δ为油套环空径向间隙，m；L为当前计算管段的长度，m；W为当前计算管段的单位长度在流体中的重力，N／m；F为当前计算管段下端的受力，N；I为当前计算管段的管段横截面积对其直径的惯性矩，m4。

对于只有部分变形的那一级管段，则可由式（27）计算，即

式（26）～（27）中的δ、F、E、I、W等值都是相应各级管柱的参数，所有各级长度变化的代数和即为因螺旋弯曲而引起的总的变形［12－13］。

①第1种情况。

式中，ΔLl为螺旋弯曲引起的管柱变形，m。

②第2种情况。

③第3种情况。

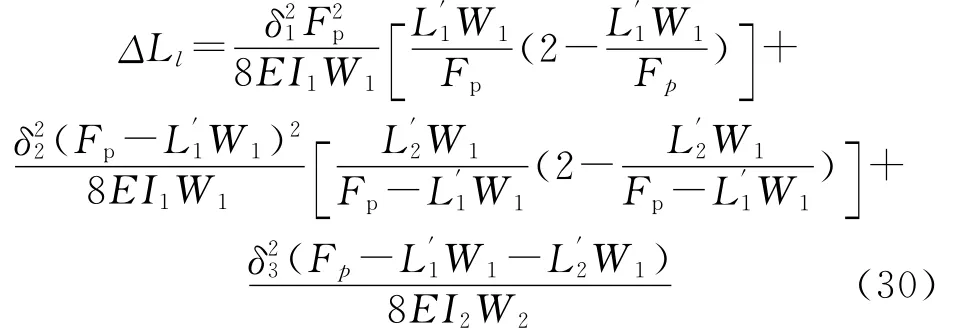
其中，L′1＋L′2＝L1。

④第4种情况。

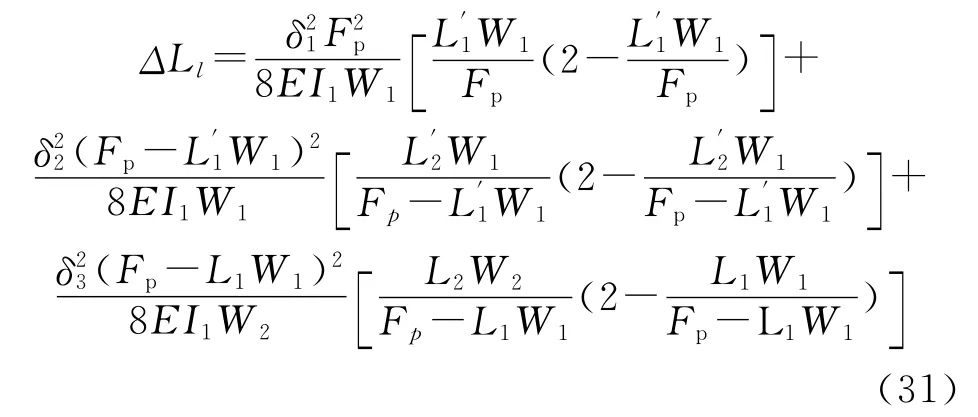
4） 弯曲段变形。

在分别求出上述变形之后，弯曲段变形为上述3个变形之和，即

式中，ΔLw为坐封后弯曲段变形，m。

其中，ΔLp、ΔLf、ΔLl根据中和点的位置分别取对应情况的值。

2.2.3 坐封后管柱直线段变形

1） 弯曲临界力引起的变形。

井内有流体时，在弯直界面上管柱的弯曲临界力为［9］

式中，FLjy为有流体时的弯曲临界力，N；Ao为油管外径包围的截面积，m2；Ai为油管内径包围的截面积，m2；poL为弯直界面管外压力，N／m2；piL为弯直界面管内压力，N／m2；FLjw为无流体时的弯曲临界力，N。

当直线段管段很长（大多数情况都满足）时，FLjw可以忽略不计，此时弯直界面受力为

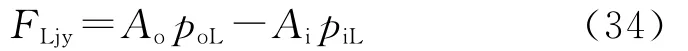
初始状态下，有

根据工程流体力学，有

将式（35）～（36）代入式（34），得

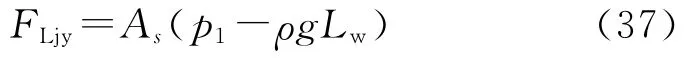
根据虎克定律，有

式中，ΔLz1为存在流体时的弯曲临界力引起的变形，m；Lz为直线段长度，m；Lw为弯曲段长度，m。

2） 释放的弯曲段油管在空气中的重力引起直线段的变形。

坐封后由于弯曲段管柱的重力被加在了封隔器上，则会引起直线段管柱的缩短变形，该变形为

式中，ΔLz2为释放弯曲段压重引起直线段变形，m；Ws为单位长度管柱在空气中的重力，N／m2。

3） 直线段变形。

坐封后直线段变形为

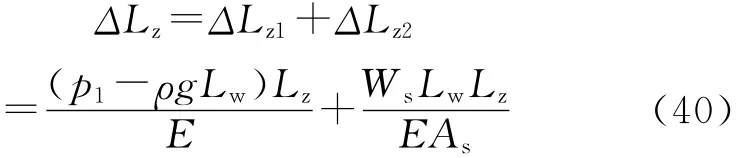
式（40）中，Lz、Lw、Ws、As根据中和点位置的不同取相应的值即可计算出不同情况下直线段的变形。

2.2.4 坐封后管柱的变形

坐封后，管柱的变形等于弯曲段变形与直线段变形之和，即

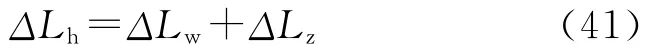
式中，ΔLh为坐封后的管柱变形量，m。

2.3 初始管柱压缩量的计算

由上述推导，初始管柱压缩量为坐封后的变形减去坐封前的变形，即

式中，ΔLcs为初始管柱压缩量，m。

根据中和点位置不同，代入前述相应的计算式可以分别求得4种情况下的初始管柱压缩量。

3 算例计算

某油井复合管柱计算参数如表1所示，井内充满液体，ρ＝1 000kg／m3；坐封时释放的压重Fp＝1.2×105N。

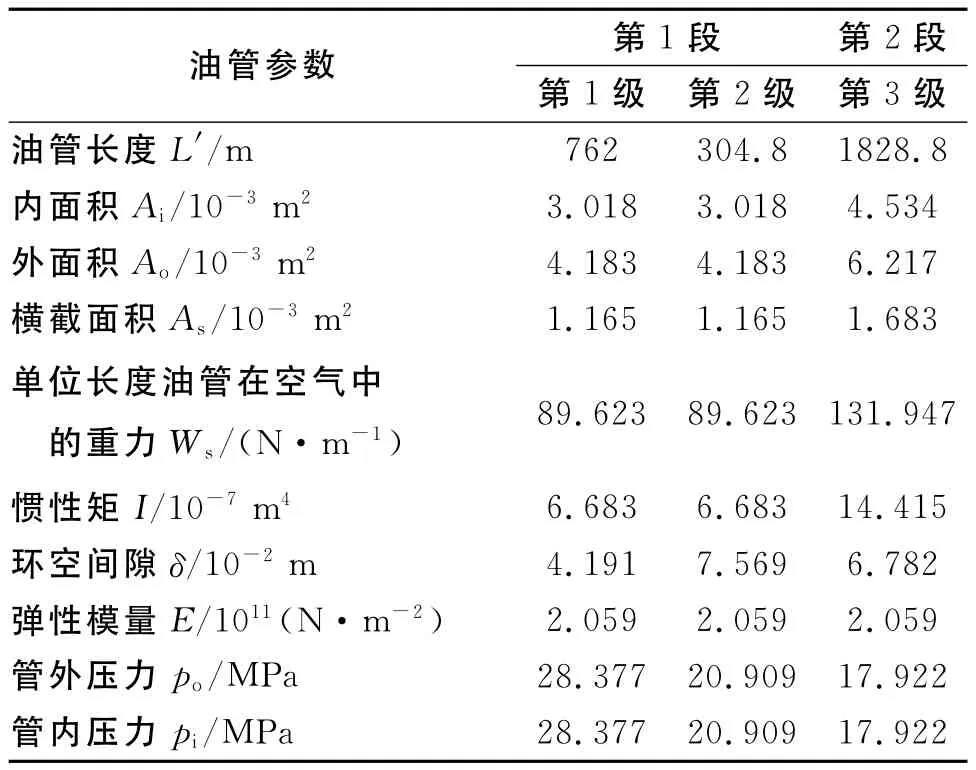
表1 油管计算参数

3.1 坐封前的变形计算

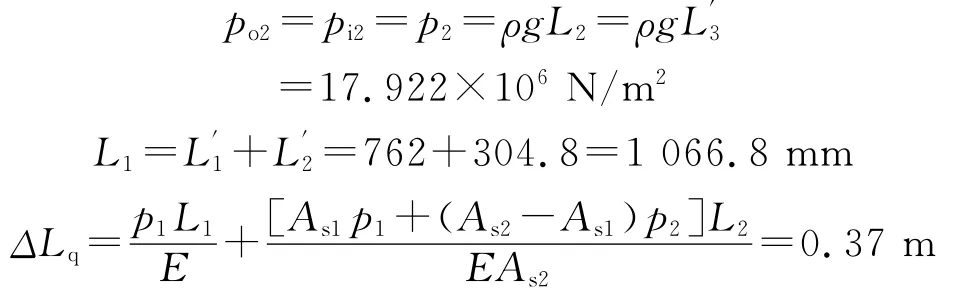
3.2 坐封后的变形计算

1） 确定中和点的位置。

由于n＞L1，则进行第2段计算，有

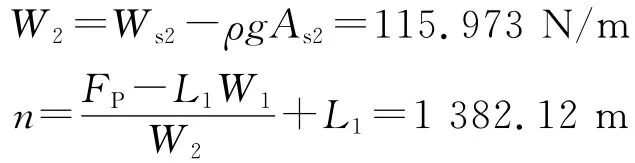
由此可知，中和点在油管第3级（第2段），距油管底部1 382.12m，属于第3种情况。

2） 弯曲段变形。

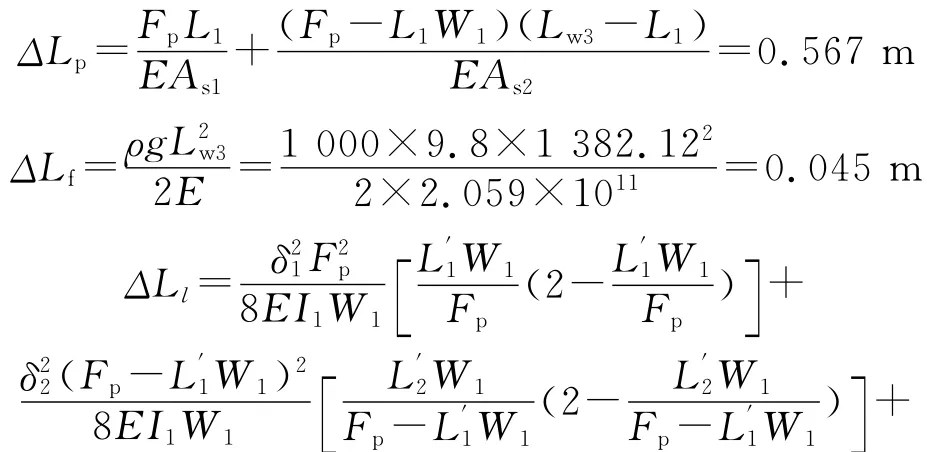
3） 直线段变形。

4） 坐封后管柱变形。

3.3 初始管柱压缩量

计算得封隔器坐封时管柱的初始压缩量为

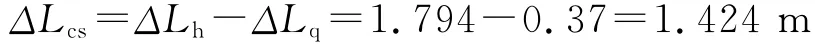
4 结论

1） 本文计算出弯曲管段的长度，以此来确定中和点的位置。根据中和点位置的不同分别给出了4种不同情况下初始管柱压缩量的计算方法，并推导了计算公式。

2） 在计算中考虑了弯曲前后流体作用力作用方式的改变而引起的变形（这是鲁宾斯基经典方法的一个缺陷），因此计算结果将更为准确。

3） 从实例计算结果可以看出，螺旋弯曲引起的变形在总的变形中占有较大比重，若不考虑螺旋弯曲将带来很大的误差。

4） 由于将螺旋弯曲的管柱与套管之间存在的摩擦未予考虑，故计算出的变形偏大，其计算结果认为是个极限值。

［1］ 江汉石油管理局采油工艺研究所，江汉石油学院采油教研室.封隔器理论基础与应用［M］.北京：石油工业出版社，1983：201－209.

［2］ 李钦道，谢光平，张 娟.初始管柱压缩量计算分析［J］.钻采工艺，2001，24（6）：48－51.

［3］ 赵广民，任 勇，张丽娟，等.组合封隔器分压管柱使用条件分析［J］.石油矿场机械，2009，38（12）：83－85.

［4］ 吕英民，陈海亮，仇伟德.材料力学［M］.东营：中国石油大学出版社，2007：18－20.

［5］ 李钦道，谢光平，张 娟.“虚力”产生的原因及特点分析［J］.钻采工艺，2001，24（5）：67－74.

［6］ 张丽娟，赵广民，赵粉霞，等.Y241型封隔器分压管柱可靠性分析［J］.石油矿场机械，2010，39（7）：25－28.

［7］ 赵广民，王艳华，任 勇，等.Y241型封隔器分压管柱及在长庆气田的应用［J］.石油矿场机械，2009，38（10）：78－80.

［8］ 马 勇，陈 平，刘中兴，等.分层压裂管柱技术在吐哈油田的应用［J］.石油矿场机械，2011，40（2）：79－83.

［9］ 李钦道，谢光平，张 娟.井内有流体时管柱弯曲临界力分析［J］.钻采工艺，2001，24（4）：44－46.

［10］ 朱洪征，姬 园，吕 旭，等.分层采油工艺管柱受力分析及优化［J］.石油矿场机械，2010，39（10）：47－50.

［11］ Lubinski A，Althouse W S，Logan J L.Helical buckling of tubing sealed in packers［J］.Journal of Petrole－um Technology，1962，14（6）：655－670.

［12］ 杜现飞，王海文，王 帅，等.深井压裂井下管柱力学分析及其应用［J］.石油矿场机械，2008，37（1）：48－50.

［13］ 岳欠杯，刘巨保，胡宝华.深井分层压裂管柱受力计算及结果分析［J］.石油矿场机械，2011，40（8）：23－28.

Analysis of Initial Quantity of Compression of Combined String

HOU Xing－hua，YANG Hui，XUE Shi－feng，ZHU Xiu－xing
（College of Pipeline and Civil Engineering，China University of Petroleum，Qingdao 266555，China）

Combined string is widely used in oil and gas well completion by packer，but the computing method of initial quantity of compression of single string is unsuited to the complex structure of combined string simply.This paper focuses on tri－combined string to calculate and locate the neutral point，and then deduces the computational formula of initial quantity of compression in four cases classified by the different location of the neutral point.Finally takes combined string structure in some oil well for example，calculates initial quantity of compression of string affected by wellbore fluid，and provides data reference to field construction.

combined string；initial quantity of compression；packer；neutral point

1001－3482（2012）07－0047－06

TE931.2

A

2012－01－22

侯兴华（1983－），男，山东莱芜人，工程师，主要从事建设规划工程技术研究，E－mail：xinghua＠upc.edu.cn。