模糊度降相关应用中的整数正交化过程研究

范 龙，翟国君，柴洪洲

(1．信息工程大学地理空间信息学院，河南郑州450052;2．海军海洋测绘研究所，天津300061)

一、引 言

GNSS定位应用中，整周模糊度能否正确解算是获得高精度位置结果的关键。模糊度解算技术经过多年的发展大体上可分为基于观测域、基于位置域和基于模糊度域等3个大类。其中，基于模糊度域的模糊度解算方法，近年来得到了广泛的研究与应用。该类方法首先在忽略模糊度整数约束的情况下获得其实数解，但由于实数解之间存在相关性，所以对实数解直接取整的方法不能获得正确模糊度值，需要基于实数解及其协方差矩阵构造相应的搜索空间对模糊度的整数解进行搜索，最后对所有整数候选值进行确认检验，从而得到最终的模糊度整数解。当各实数解之间相互独立时，基于实数解及其协方差矩阵构造的搜索空间呈标准的球体，然而由于相关性的存在，其搜索空间实为椭球体，并且相关性越强，椭球体的形状越扁长。模糊度搜索的效率和成功率受到搜索空间形状的影响，甚至可能造成搜索固定失败。为保证效率和成功率，在模糊度搜索之前需要对实数解进行降相关变换。文献[1]基于整数高斯变换，提出了LAMBDA算法;文献[2]对LAMBDA算法的整个过程进行了详细介绍，并提出了系统配对的策略来构造Z变换矩阵;文献[3-4]提出了基于Cholesky分解的模糊度降相关算法;文献[5]提出了多次整数三角分解降相关的方法;文献[6]提出了用递归的方法直接最小化转换矩阵的对角线元素的方法;文献[7]提出了对模糊度协方差矩阵的对角线元素进行排序的降相关算法。以上几种算法均是利用数学领域中的矩阵变换算法，使模糊度协方差矩阵能够尽可能地对角化。文献[8]将数学领域中为解决格理论的相关问题而提出的著名的LLL规约算法进行了转化，并将其应用到模糊度降相关中;文献[9]对整数高斯变换、整数Cholesky分解及LLL算法进行了分析比较;文献[10]针对LLL降相关算法在取整过程中会引入较大的舍入误差的问题，提出了基于矩阵整体进行取整的改进的LLL算法;文献[11]提出了基于修正的Gram-Schmidt正交化(MGS)变换[12]的 LLL 算法。

LLL算法通过利用整数GS正交变换对模糊度矩阵进行降相关处理，本文对该算法的正交变换过程进行了分析，并依照标准的GS正交变换过程，指出了LLL算法采用的正交变换过程在降相关应用中会在舍入误差的基础上引入新的误差，且该误差会随着算法的迭代而累积，最终甚至可能造成降相关失败。为此，本文依照标准GS变换，对LLL算法的整数正交变换过程进行了改进，利用随机模拟的数据进行了计算分析，结果表明对整数正交变换过程改进后，LLL算法的降相关效果有了明显的改善，并且变换后的协方差矩阵更加有利于模糊度的搜索固定。

二、LLL降相关中整数正交化过程的分析与改进

对于通用GNSS定位模型

式中，L为观测向量;A为位置参数的设计矩阵;x为三维的位置、大气延迟等未知的改正参数;a为模糊度参数;B为其相应的系数矩阵。考虑观测值权矩阵为P，在取消模糊度向量a的整数约束的情况下，利用标准的最小二乘平差，可得其实数解 ^a，及其相应的方差阵

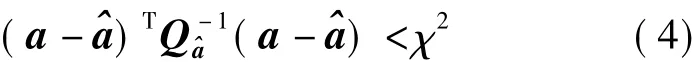
式中，χ2是人为设定的，该值会影响到搜索空间的大小，而模糊度实数解的方差阵则会影响到搜索空间的形状，实数解之间较强的相关性，使得搜索空间又扁又长，影响到模糊度的搜索效率，甚至搜索不到整数值[1]。为改善这种情况，可以对模糊度的实数解进行一系列变换，降低它们之间的相关性。为了保证转换过程中的整数特性及搜索空间大小的不变性，要求变换矩阵的所有元素必须是整数，且逆矩阵也是整数即变换矩阵的秩为1，同时经过变换后模糊度的方差必须变小[1，9，13]。

为了使Q^a能够对角化，需要通过变换使得H矩阵的列向量之间能够相互正交。LLL算法基于Gram-Schmidt正交化的方法进行处理，利用该正交化算法可将矩阵变换为列向量之间相互的矩阵假设H矩阵的前k-1个向量已经进行了正交变换，得到，则 hk首先与 q1进行正交化变换

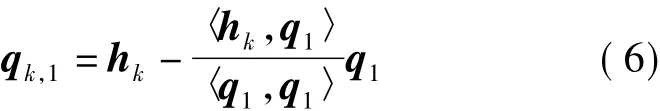
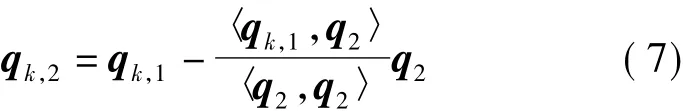
为了保证变换过程不破坏模糊度未知参数的整数特性，LLL算法中的整数正交化变换，对式中系数tik直接取整，采用如下式所示的过程进行处理

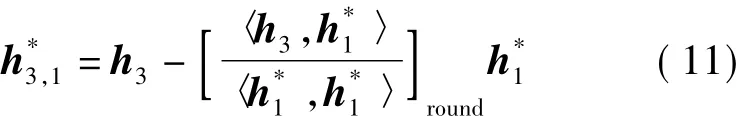
其相当于在取整引入舍入误差的基础上，又引入了新的误差ε3

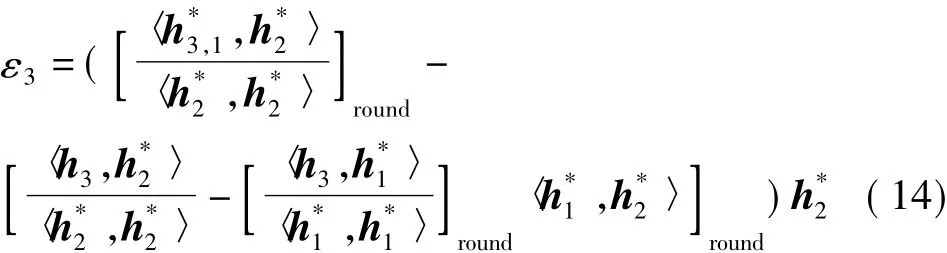
该误差是由于经过整数GS变换后的向量之间不能完全正交而引起的。随着对其余向量逐一进行正交变换，该误差还会累积，越往后影响越大。这就说明在构造整数正交变换过程中，应当依据标准GS正交变换的原理，对于每个向量，应采用如下式所示的正交化过程。对于k=2，3，…，n

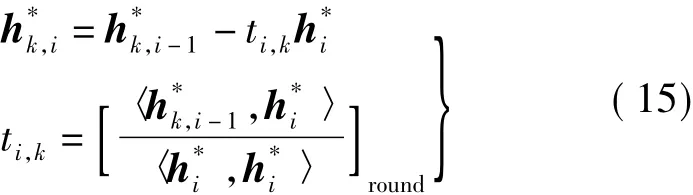
三、计算分析

由于每一对模糊度未知参数都对应一组观测值及相应的卫星和测站之间的几何结构，若只用一个模糊度实数解的方差协方差矩阵来进行计算分析，就会陷入到该特殊情况之中，由该例子反映出的每种方法降相关方法的优劣，不具有绝对的说服力。为不失一般性，本文采用随机模拟的方法计算出模糊度实数解的协方差矩阵，分别利用LLL降相关算法和整数正交化过程经过改进的LLL算法进行计算分析。

笔者模拟了100组模糊度协方差矩阵，为了显示各算法的降相关效果，以降相关变换前后的平均相关系数γ和条件数c作为依据，通过降相关变换可得如图1所示的结果。

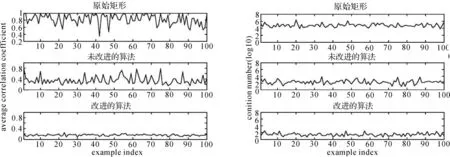
图1 变换前后的平均相关系数和条件数

图1中左边为平均相关系数的变化，右边为条件数的变化。由相关定义可知，平均相关系数反映实数解之间的平均相关性，该值越接近1说明相关性越强。如图1所示，未进行降相关变换之前，原始协方差矩阵的平均相关系数基本都在0．5～1的范围内变化，说明原始协方差矩阵具有较强的相关性，同时矩阵的条件数也很大，在1．0e4～1．0e6的范围变化，矩阵呈现出病态性。经过变换后无论平均相关系数还是条件数都有所改善，从图1中可以看出对于这100组数据，改进算法对于两种指标的改善效果明显优于未改进的算法。通过计算，所有数据相关指标的均值见表1。

表1 平均相关系数及条件数的均值

为了进一步验证本文所提算法对于模糊度搜索固定的贡献，笔者从中选取了5组数据，在分析其平均相关系数和条件数变化的基础上，计算其相应的 Bootstrapping算法的成功率[4]，结果见表2。

表2 条件数、相关系数及Bootstrapping成功率的统计

由表2中可以看出模拟的协方差矩阵的相关性很强，从而导致Bootstrapping算法的成功率很低。经过未改进的正交化算法虽然能够改善矩阵的相关性，但是在某些历元由于舍入误差的累积的影响，其降相关的效果不理想，处理后的Bootstrapping成功率虽然有所提高，但是仍不能满足100%成功的要求;改进后的算法无论在平均相关系数还是条件书的改进方面都优于未改进时的情况，其Bootstrapping算法可达到100%的成功率。

四、结 论

本文依照标准的GS正交化过程对LLL降相关算法中的整数正交变换的过程进行了分析，针对算法在变换过程会造成取整舍入误差累积的情况进行了改进，通过比较分析得出如下结论：

1)LLL算法中整数正交变换的向量正交化过程，在取整舍入误差的基础上还会受到向量之间不能完全正交而引起误差的影响，该误差随着正交化的进行会逐渐累积，最终影响降相关的效果。

2)在对该误差分析的基础上，依据标准的GS正交化过程，对向量的整数正交化变换过程进行了改进，通过对模拟数据的计算比较，验证了改进的正交化过程能够较好地改善LLL算法降相关效果不佳的问题。

[1]TEUNISSEN P．The Least-squares Ambiguity Decorrelation Adjustment：a Method for FastGPS Integer Ambiguity Estimation[J]．Journal of Geodesy，1995，70(1-2)：65-82．

[2]JONGE P，TIBERIUSC．The LAMBDA Method for Integer Ambiguity Estimation：Implementation Aspects[R]．Delft：Delft University of Technology，1996．

[3]TEUNISSEN P．A New Method for Fast Carrier Phase Ambiguity Estimation[C]∥ Proceedings of IEEE PLANS’94．Las Vegas：[s．n．]，1994：562-573．

[4]周扬眉，刘经南，刘基余．回代解算的LAMBDA方法及其搜索空间[J]．测绘学报，2005，34(4)：300-304．

[5]HAN S．A New Method for Constructing Multi-satellite Ambiguity Combinations for Improved Ambiguity Resolution[C]∥Proceedings of ION GPS-95．[S．l．]：Palm Springs，1995：1145-1153．

[6]LIZ，GAO Y．A Method for Construction of High Dimension Transformation Matrices in LAMBDA[J]．Geomatica，1998(52)：433-439．

[7]LIU L T，HSU H T，ZHU Y Z，et al．A New Approach to GPSAmbiguity Decorrelation[J]．Journal of Geodesy，1999，73(9)：478-490．

[8]GRAFAREND E．Mixed Integer-real Valued Adjustment(IRA)Problems：GPS Initial Cycle Ambiguity Resolution by Means of the LLL Algorithm[J]．GPSSolutions，2000，4(2)：31-44．

[9]XU Peiliang．Random Simulation and GPSDecorrelation[J]．Journal of Geodesy，2001，75(7-8)：408-423．

[10]刘志平，何秀凤．改进的GPS模糊度降相关LLL算法[J]．测绘学报，2007，36(3)：286-289．

[11]杨荣华，花向红，李昭，等．GPS模糊度降相关LLL算法的一种改进[J]．武汉大学学报：信息科学版，2010，35(1)：21-24．

[12]张贤达．矩阵分析与应用[M]．北京：清华大学出版社，2004．

[13]TEUNISSEN P．The Invertible GPSAmbiguity Transformations[J]．Manuscripta Geodaetica，1995(20)：489-497．

[14]HATCH R，EULER H J．Comparison of Several AROF Kinematic Techniques[C]∥Proceedings of IEEE Symposium on Position，Location and Navigation．Salt Lake City：IEEE，1994：363-370．

[15]FREIE，BEUTLER G．Rapid Static Positioning Based on the Fast Ambiguity Resolution Approach“FARA”Theory and First Results[J]．Manuscripta Geodaetica，1990(11)：325-356．

[16]TEUNISSEN P．The Success Rate and Precision of GPS Ambiguities[J]．Journal of Geodesy，2000，74(3-4)：321-326．

[17]TEUNISSEN P，JONG P，TIBERIUSC C．The Leastsquares Ambiguity Decorrelation Adjustment：Its Performance on Short GPSBaselines and Short Observation Spans[J]．Journal of Geodesy，1997，71(10)：589-602．

[18]LENSTRA A K，LENSTRA H W，LOVASZ L．Factoring Polynomials with Rational Coefficients[J]．Mathe matische Annalen，1982，261(4)：515-534．

[19]赵韬，姜金荣．分块Gram-Schmidt正交化算法及其应用[J]，中国科学院研究生院学报，2009，26(2)：224-229．

[20]JALBYW，PHILIPPEB．Stability Analysis and Improvement of the Block Gram-Schmidt Algorithm[J]．SIAM Journal on Scientific and Statistical Computing，1991，12(5)：1058-1073．

[21]STATHOPOULOS A，WU Keskeng．A Block Orthogonalization Procedure with Constant Sysnchronization Requirements[J]．SIAM Journal on Scientific and Statistical Computing，2002，23(6)：2165-2182．

[22]刘志平，何秀凤，郭广礼，等．GNSS模糊度降相关算法及其评价指标研究[J]．武汉大学学报：信息科学版，2011，36(3)：257-261．