CdnSn(1≤n≤12)团簇结构与电子性质的密度泛函理论研究
2012-12-10楚合营刘朝霞罗华平张景川胡芸莎
楚合营 刘朝霞 罗华平 张景川 胡芸莎
(塔里木大学机械电气化工程学院,新疆阿拉尔 843300)
Ⅱ-Ⅵ族半导体材料由于具有独特的物理和化学性质,一直深受研究人员的关注[1-5]。例如ZnO、ZnS、CdS、CdSe等都是直接带隙半导体,其能隙覆盖了整个可见光范围,因而是一类具有广泛应用前景的光敏材料。随Ⅱ-Ⅵ族半导体量子点实验研究的不断深入,Ⅱ-Ⅵ族半导体材料的理论研究也越来越受到科学家的重视,特别是对Ⅱ-Ⅵ族半导体团簇的理论研究[5-14]。与有机发光材料相比,CdS这种无机量子点不仅具有丰富的颜色,而且能够承受多次的激发和光发射而不会分解,因此CdS这种无机量子点可以作为示踪粒子或分子标签在生物化学、分子生物学、细胞生物学、基因组学、蛋白质组学、药物筛选和生物大分子相互作用等研究中扮演重要角色。对CdnSn半导体团簇进行研究,有助于人们对CdS量子点光学以及电子性质的研究。但是,由于团簇的电子性质对团簇的结构比较敏感,同时随着原子个数的增加,团簇的初始结构成指数增长,计算工作量也越来越大,因此给较大CdnSn半导体团簇的理论研究带来了极大的挑战。根据文献报道,相对其它Ⅱ-Ⅵ族半导体团簇而言,对CdnSn半导体团簇的研究文献报道还比较少。因此,进一步开展对CdnSn半导体团簇的研究对于认识CdS量子点以及CdnSn半导体团簇的生长方式和电子性质都是十分必要的。利用Dmol3模拟软件包对CdnSn(1≤n≤12)团簇的几何构型进行优化,并对其能量、频率以及电子性质进行了模拟分析。
1 计算方法
在Dmol3软件包上,采用密度泛函理论(DFT)下的广义梯度近似(GGA)对CdnSn(1≤n≤12)团簇的几何结构进行优化,并对其电子性质进行计算机模拟。在广义梯度近似下,选用Perdew-Wang(PW91)交换关联泛函。为了获取最精确的计算数据,所有的计算均是在Fine网格下完成的,采用带极化的双数值原子基组(DNP)进行全电子计算,自洽过程以体系的能量和电荷密度分布是否收敛为依据,精度均优于10-5a.u.,梯度和位移的收敛精度优于2.0 ×10-3a.u./nm 和 5.0 ×10-3nm,能量的收敛精度优于1.0 ×10-5a.u.。CdnSn 半导体团簇的初始构型,在借鉴文献[11-14]报道的Ⅱ-Ⅵ族半导体团簇结构的基础上,进行了进一步的扩充。
2 结果与分析
2.1 团簇结构分析
由于团簇的结构决定了团簇的物理和化学性质,所以在团簇研究中团簇的结构就成为团簇研究中的一项主要研究内容。在对CdnSn(1≤n≤12)半导体团簇的初始构型进行几何结构优化的同时对团簇的振动频率进行了计算,把总能量最低且最小振动频率为正值的结构确定为团簇的最低能量结构。团簇的能量越低,团簇也就越稳定。图1给出了CdnSn(1≤n≤12)半导体团簇的最低能量结构。表1列出了CdnSn(1≤n≤12)半导体团簇的最低能量结构下的对称性(Symmetry),Cd-S键长(R),能隙(Egap),平均结合能 Eb=(nECd+nES-ECdnSn)/2n,Cd和S的Mulliken原子电荷数(Q),最低振动频率(ωmin)。
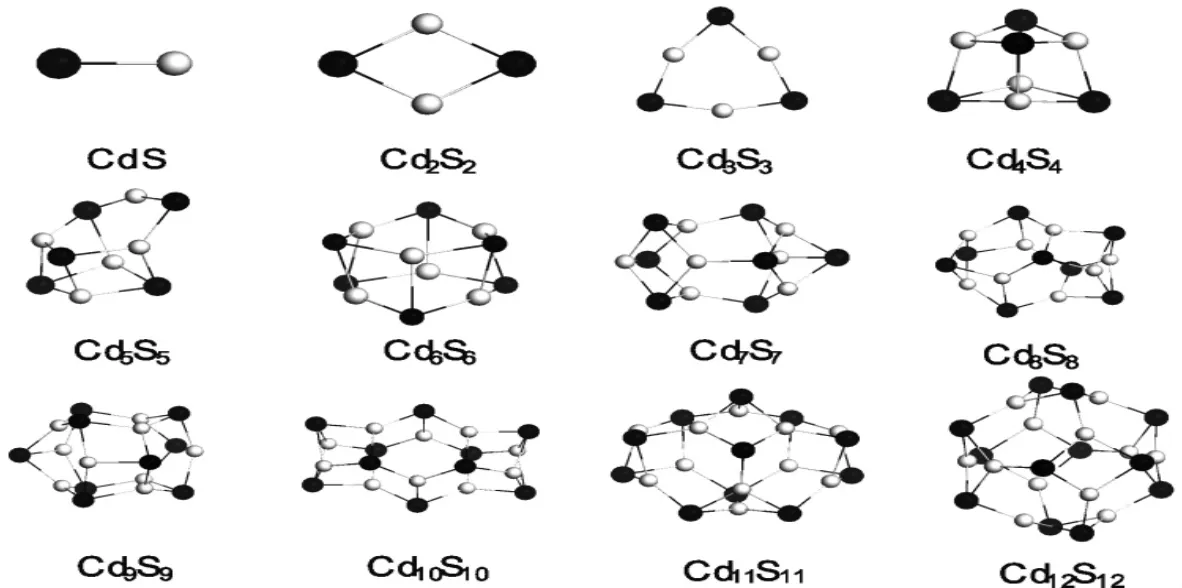
图1 CdnSn(1≤n≤12)半导体团簇的最低能量结构(黑色小球代表硫原子,灰色小球代表镉原子)
如图1所示,n=1时团簇的结构最为简单,计算结果显示CdS团簇的对称性为Cinfv,Cd-S键长为2.36埃,平均结合能和能隙分别为1.010 eV·atom-1和0.233eV,与文献[11]给出 Cd - S 键长的计算结果相一致,并且接近于实验值(2.52埃),这说明选取的计算参数是准确的,而且在Fine网格下对团簇结构及电子性质进行模拟也是必要的。当n=2时,计算结果显示Cd2S2的最低能量结构是平面结构,团簇的对称性为D2h,键长为2.50埃,能隙为1.218 eV。当n=3时,Cd3S3团簇的最低能量结构仍然是平面结构,团簇的对称性为D3h,键长为2.43埃,能隙为2.542 eV。从图1 CdnSn团簇的最低能量结构可以看出,Cd2S2和Cd3S3团簇的最低能量结构可以看成是组成4≤n硫化镉团簇最低能量结构的两个亚单元。
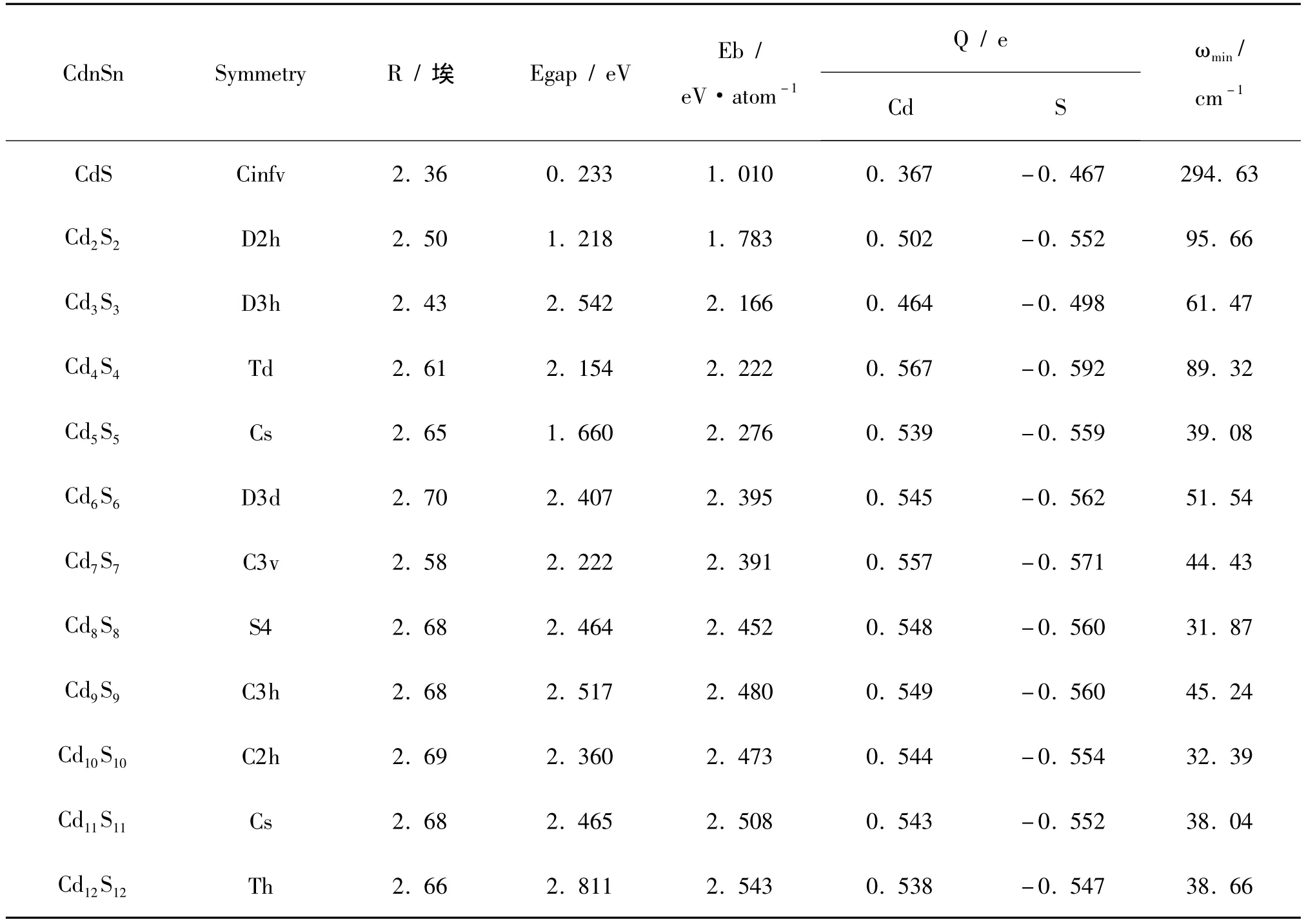
表1 CdnSn(1≤n≤12)团簇最低能量结构下的对称性(Symmetry),Cd-S键长(R),能隙(Egap),平均结合能(Eb),Cd和S的Mulliken原子电荷(Q),最低振动频率(ωmin)
当n=4时,CdnSn团簇的最低能量结构不再是平面结构,而是三维笼状结构,如图1所示。Cd4S4可以看成是由6个Cd2S2单元相互连接而成的多面体,Cd4S4的对称性为Td、键长为2.61埃、能隙为2.154eV、平均结合能为2.222 eV·atom-1。当n=5时,Cd5S5团簇的最低能量结构可以看成是由4个Cd2S2和两个畸变的Cd3S3连接而成。当n=6时,团簇Cd6S6的最低能量结构可以看成是由6个Cd2S2和两个Cd3S3亚单元连接而成。当n=7时,从图1可以看出Cd7S7团簇的最低能量结构可以看成是由6个Cd2S2和3个Cd3S3亚单元构成的一个完美的笼。当n=8时,Cd8S8可以看成是由6个Cd2S2和4个Cd3S3亚单元相互连接而成。当n=9时,团簇Cd9S9可以看成是由Cd2S2和Cd3S3两个亚单元组成的笼型结构。随着团簇原子个数的增加,团簇的初始结构迅速的增多,为了减少计算工作量,在构建团簇初始结构时尽量多的使用Cd2S2和Cd3S3团簇的最低能量结构作为构建团簇的亚单元,结果显示这种尝试是非常有效的。

图2 CdnSn(1≤n≤12)团簇的总能量二阶有限差分△2E(n)=E(n-1)+E(n+1)-2E(n)随n的变化关系
当n=10时,团簇Cd10S10的能量最低能量结构可以看成是由6个Cd2S2和6个Cd3S3团簇亚单元构建成的笼状团簇,显然随着团簇原子个数的增加,团簇的结构越来越复杂。当n=11时,Cd11S11可以看成是由6个Cd2S2和7个Cd3S3团簇基元构建成的。当n=12时,Cd12S12则可以看成是由6个Cd2S2和8个Cd3S3团簇的亚单元组成的球状结构,从而使由Cd2S2和Cd3S3两个亚单元构成CdnSn团簇最低能量结构达到了一个极致。从表1给出的CdnSn(1≤n≤12)团簇最低能量结构下的对称性(Symmetry),Cd-S键长(R),能隙(Egap),平均结合能(Eb),Cd和S的Mulliken原子电荷(Q),最低振动频率(ωmin)不难看出,随着n的增加团簇的性质逐渐向CdS晶体的性质过渡。这说明图1给出的CdnSn(1≤n≤12)团簇的生长规律是合理的。
综上所述,当n≤3时,团簇的最低能量结构为平面结构;当4≤n≤12时,团簇的最低能量结构为三维笼状结构。值得注意的是4≤n≤12团簇的最低能量结构可以看成是由团簇Cd2S2或Cd3S3两个亚单元构成。这和文献[11-14]报道的 ZniSi,CdnSen,CdnSn团簇的最低能量结构相似。从图1 CdnSn(4≤n≤12)团簇的最低能量结构不难看出,镉和硫每个原子的配位数都为3,而镉原子与硫原子的最外层电子排布分别为4d105s2和3s23p4,因此CdnSn(4≤n≤12)团簇的最低能量结构里的镉原子与硫原子最外层电子容易形成SP2杂化,从而降低了硫化镉团簇的总能量。
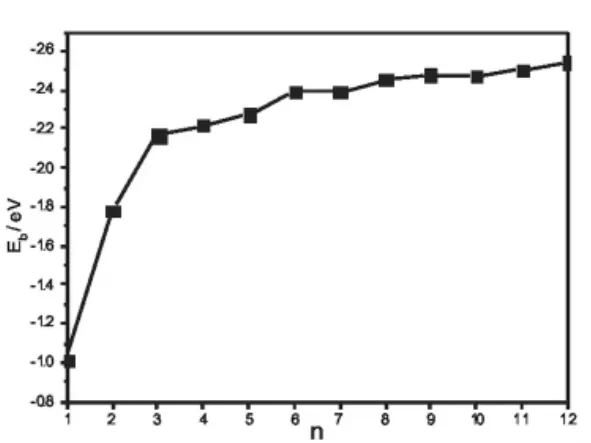
图3 CdnSn(1≤n≤12)最低能量结构团簇的平均结合能Eb=(nECd+nES-ECdnSn)/2n随n的变化曲线
2.2 电子性质分析
为了研究团簇的相对稳定性,图2给出了硫化镉团簇的总能量二阶有限差分(△2E(n)=E(n-1)+E(n+1)-2E(n))随n的变化关系。众所周知,团簇的总能量二阶有限差分是反映团簇的相对稳定性比较灵敏的一个物理量。从图2可以看出,在n=3、6和9处出现了极大值,这表明n=3、6和9为半导体团簇CdnSn(1≤n≤12)的幻数。团簇Cd3S3,Cd6S6和Cd9S9在实验制备时的丰度会相对比较大。
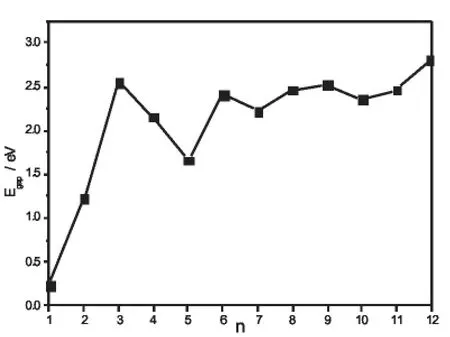
图4 CdnSn(1≤n≤12)半导体团簇的能隙EGap随n的变化规律曲线
图3给出了半导体团簇CdnSn(1≤n≤12)最低能量结构的平均结合能Eb随n的变化曲线。团簇的平均结合能Eb是也反映团簇相对稳定性的一个重要物理量。从图3不难看出,随着团簇尺寸的增加,团簇最稳定结构的平均结合能逐渐增大,这说明团簇在生长过程中能继续获得能量。在n=3、6和9处出现了极大值,这进一步表明团簇Cd3S3、Cd6S6和Cd9S9比它们邻近的团簇更稳定。这也从另一个方面说明半导体团簇CdnSn(1≤n≤12)的幻数为n=3、6 和9。
为了更进一步研究团簇的相对稳定性,图4给出了团簇的最高已占据轨道(HOMO)与最低未占据轨道(LUMO)之间的能隙Egap随团簇尺寸的变化规律。能隙反映了电子从占据轨道向未占据轨道发生跃迁的能力,在一定程度上反映了团簇参与化学反应的能力。从图4不难看出,与近邻的团簇相比,团簇 Cd3S3、Cd6S6和 Cd9S9的能隙较大,这表示Cd3S3、Cd6S6和Cd9S9团簇的化学活性比较弱,也就是说团簇Cd3S3、Cd6S6和Cd9S9相对稳定一些。这与前面团簇的总能量二阶有限差分以及团簇最低能量结构下的平均结合能的分析结果相一致。表1给出的Cd3S3、Cd6S6和 Cd9S9团簇的能隙分别为2.542eV、2.407eV和2.517eV,比其相邻的团簇的能隙都要大一些儿。这更进一步说明n=3、6和9为CdnSn(1≤n≤12)半导体团簇的幻数。同时,显示Cd3S3、Cd6S6和Cd9S9可能是构成CdS量子点的重要组成部分,这对于研究小于1nm的CdS量子点的结构以及电子性质具有重要的理论价值。更值得一提的是模拟结果显示硫化镉团簇的能隙Egap与平均结合能Eb随团簇尺寸n的变化规律完全一致,这说明图1给出的硫化镉团簇的最低能量结构是合理的,表1给出的模拟数据也是准确可靠的。
3 结论
采用基于密度泛函理论的广义梯度近似对CdnSn(1≤n≤12)半导体团簇的几何结构进行了优化,并对其总能量、振动频率以及电子性质进行了模拟。结果显示,当n≤3时,团簇的最低能量结构为平面结构;当4≤n≤12时,团簇的最低能量结构为三维笼状结构。4≤n≤12团簇的最低能量结构可以看成是由团簇Cd2S2或Cd3S3两个亚单元构成。CdnSn(1≤n≤12)半导体团簇的总能量二阶有限差分△2E(n),平均结合能Eb以及能隙Egap都表明n=3、6和9为团簇的幻数。CdnSn(4≤n≤12)团簇的最低能量结构里的镉原子与硫原子最外层电子形成SP2杂化,是造成团簇能量较低的主要原因。
[1]Ma Hong,Ma Guo-Hong,Wang Wen -Jun,et al.Size-dependent optical properties and carriers dynamics in CdS,ZnS quantum dots[J].Chin.Phys.B,2008,17:1280.
[2]Wu Si-Xin,Chu He-Ying,Xu Hong-Tao,et al.Oscillation of absorption bands of Zn1-xMnxS clusters:an experimental and theoretical study[J].Nanotechnology,2008,19:055703.
[3]Antonietta Tomasulo,Mushti V.Ramakrishna.Quantum confinement effects in Smiconductor clusters.II[J].J.Chem.Phy.,1996,105:3612-3626.
[4]Claudia Troparevsky M,Leeor Kronik,James R.Chelikowsky.Optical properties of CdS quantum dots[J].Phys.Rev.B,2001,65:033311.
[5]Jan - Ole Joswig,Michael Springborg,Gotthard Sifert.Structural Electronic Properties of Cadmium Sulfide Clusters[J].J.Phys.Chem.B,2000,104:2617 -2622.
[6]Trave A,Buda F,Slloni A.CdS Microclusters in Sodalite Frameworks of Different Composition A Density Functional Study[J].J.Phys.Chem.B,1998,102:1522-1527.
[7]Claudia Troparevsky M,James R.Chelikowsky.Structural and electronic properties of CdS and CdSe clusters[J].J.Chem.Phys.,2001,114:943 -949.
[8]Claudia Troparevsky M,Leeor Kronik,James R.Chelikowsky.Ab initio absorption spectra of CdSe clusters[J].J.Chem.Phys.,2004,119:2284 -2287.
[9]李春霞,党随虎,张可言,等.应用第一性原理对CdSe和HgTe团簇结构和电子性质的研究[J].原子与分子物理学报,2008,25:542.
[10]李春霞.中小尺寸CdS和CdTe团簇结构与电子性质的第一性原理研究[J].原子与分子物理学报,2007,24:1060.
[11]Chu H -Y,Liu Z-X,Qiu Guo-Li,et al.Firstprinciples study of structures and electronic properties of cadmium sulfide clusters[J].Chin.Phys.B,2008,17:2478-2483.
[12]CdnSen(1≤n≤12)团簇结构与电子性质的第一性原理研究,刘朝霞,楚合营,胡芸莎,等.原子与分子物理学报,2011,28,0048.
[13]Jon M.Matxain,JoSph E.Fowler,and Jesus M.Ugalde.Small clusters of II-VI materials ZniSi(i=1-9)[J].Phys.Rev.A,2000,61:053201.
[14]Eleonora Spano,Said Hamad,C.Richard A.Catlow.Computational Evidence of Bubble ZnS Clusters J.Phys.Chem.B,2003,107:10337-10340.
