基于Datcom软件的巡航靶弹气动估算*
2012-12-10韩京霖陈光学
韩京霖,王 铮,陈光学
(陕西中天火箭技术有限责任公司,西安 710025)
0 引言
在导弹初步设计过程中,经济而快速地计算其气动参数十分重要。导弹最终气动外形及气动力特性取决于导弹的分系统,如有效载荷的尺寸、动力系统和发射装置等,而这些分系统在导弹设计初期是需要反复修改的,因此设计者必须能够精确而快速的预测大范围变化的导弹气动外形。计算流体力学(CFD)方法可以较准确的计算导弹气动参数,但其计算量太大,导弹每修改一次外形都要消耗较长的计算时间和人力成本,不适合在初步设计过程中使用;而美国空军开发的Missile Datcom软件可在大范围内快速预估一系列导弹气动外形。文中选取某巡航靶弹,在其主要工况下采用Datcom方法对其进行气动特性估算,并对比其CFD的计算结果加以分析。
1 Datcom软件简介
Datcom软件利用美国几十年来的风洞试验数据建立典型气动模型,采用部件组合、数据和方法模块化等方法,针对一般外形的导弹在一定飞行条件下的估算结果具有较高精度。
1.1 Datcom软件对导弹外形要求
Datcom软件适用于以下外形的导弹:
1)轴对称的或椭圆形截面的弹身;
2)沿弹身从头锥到尾部有一到4组气动力面装置,每组气动力面装置可以由1~8个相同的面板组成,这些面板具有相同的纵向位置,每个气动力面可以独立的偏转,或以全动偏转或以平面后缘襟翼偏转。
1.2 气动力估算方法
Datcom在估算中使用了经验与理论相结合的方法,并基于导弹的几何布局和飞行条件对方法进行选择。使用时,首先对导弹弹体和弹翼的气动参数分别进行估算,再使用不同的组合系数和方法将它们组合起来,最终得到全弹的气动参数。
1.2.1 单独弹体的方法
对于亚音速的单独弹体,Datcom使用“组合气动估算方法”。在小攻角下(小于5°~10°),采用经验关系以及细长体理论计算法向力和俯仰力矩。
法向力系数计算公式:

式中,CP为压力系数,可由速度势微分得到:

俯仰力矩系数计算公式:

在大攻角下,采用艾伦和帕金斯的粘性流理论,将法向力及俯仰力矩都分为位流项和粘性项,分别计算再线性叠加:

式中:CNα为法向力随攻角变化率;CDc为横流阻力系数。
轴向力的计算也采用了两种不同的方法:在30°攻角以下,采用修正版的艾伦和帕金斯理论;在30°攻角以上,采用约根森的细长体理论,通过降低沿弹身的动压来对轴向力进行修正。不同攻角产生不同的轴向力;而由表面摩擦、波、压力以及底阻产生的轴向力认为与攻角无关,并全部包括在总的轴向力中。轴向力系数计算公式如下:

式中:CA,0为零升轴向力系数;CA,α为有升力时轴向力系数。
1.2.2 单独弹翼的方法
计算单独弹翼气动参数的方法与弹体类似。法向力和俯仰力矩的计算分线性与非线性两部分,分别计算并求和。
法向力系数计算公式:

式中:CNαα为非线性部分法向力随攻角变化率,当攻角较大时,该项在法向力中起主要作用,并随攻角和翼型特性的变化而变化。
俯仰力矩系数计算公式:

式中:CN,p为位势法向力系数,设作用在翼的压心;CN,v为粘性法向力系数,设作用在翼的形心。
弹翼轴向力的计算与弹体一样。攻角独立于表面摩擦、压力、波以及底阻进行计算,不同攻角产生的轴向力将加入到总的轴向力中。计算公式如下:

1.2.3 部件组合方法
计算组合的弹体和弹翼的气动参数时,考虑部件干扰效应。对于线性范围的攻角(如小于5°),由尼尔森、皮特和卡塔利提出的方法计算弹体和弹翼的传递载荷。虽然这个方法只在线性范围内有效,但它可以以合理的置信度推广到10°攻角范围。超过10°攻角时,采用“等效攻角”(假设翼法向力的影响可以表示为攻角增量,并和原攻角加到一起形成一个等效攻角)的方法计算,该方法可计算到30°攻角。对于30°以上攻角,虽然软件仍可运行,但此时该方法的有效性未经校验和证明。
2 计算与分析
该巡航靶弹头锥为半椭球形,弹体为旋成体,采用正常式布局,弹翼和舵面均为六边形,呈×-×配置,如图 1所示。模型结构简单,满足使用Datcom估算的结构要求。

图1 导弹模型
2.1 CFD计算
首先对巡航靶弹进行CFD气动力计算,采用的软件为FLUENT。选取飞行条件为海拔0m,标准大气,马赫数Ma=0.7,攻角 α =4°,分别在舵偏 δ=0°和5°下建模计算。由于靶弹为面对称形,故使用FLUNENT前处理软件Gambit对靶弹建立半模型,而后导入FLUENT,选择基于密度的显式求解器,湍流模型采用k-ω双方程模型及雷诺应力模型。经数天计算,部分计算结果如图2、图3所示。
图2 弹体表面速度矢量

图3 弹体表面压力分布云图
2.2 Datcom计算
选择在5 个马赫数(0.3,0.5,0.7,1.1,2.0)和 8个攻角(-15°,-10°,-4°,0°,1°,4°,10°,15°)状态下计算,耗时很短,最多半天便可完成全部计算。限于篇幅,文中给出部分计算结果。图4、图5分别是舵偏δ=0°和5°下导弹的法向力系数CN,图6是舵偏δ=0°时导弹的轴向力系数CA,图7是舵偏δ=0°时导弹的俯仰力矩系数Cm。
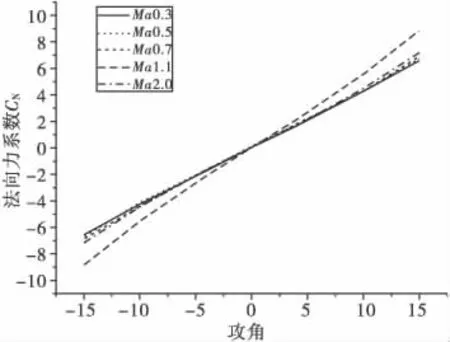
图4 CN与 Ma、α 变化曲线(δ=0°)

图5 CN与 Ma、α 变化曲线(δ=5°)
由图4、图5可以看出,法向力系数随攻角的增大而增大,两者基本呈线性关系;与马赫数关系较小。
由图6可以看出,轴向力系数在正攻角范围内,随攻角增大而增大;在负攻角范围内,随攻角的增大而减小;当攻角为0°时达到最小值。在低马赫数下,轴向力系数随攻角增加较慢;在高马赫数下,轴向力系数随攻角增加较快。

图6 CA与 Ma、α 变化曲线(δ=0°)
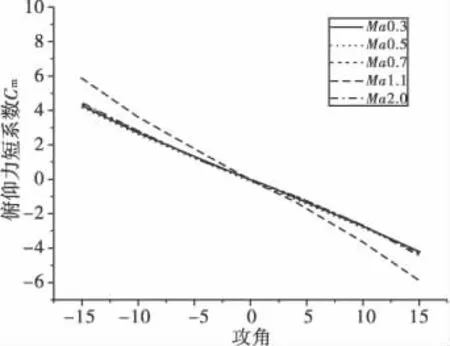
图7 Cm与 Ma、α 变化曲线(δ=0°)
由图7可以看出,俯仰力矩系数随攻角的增大而减小,两者基本呈线性关系,与马赫数关系较小。由于俯仰力矩系数对攻角的导数小于零,所以靶弹静稳定,符合设计要求。
2.3 对比分析
在Ma=0.7,α =4°下,比较CFD与Datcom的计算结果(表1)。由于在方案设计阶段,最重要的是精确估算靶弹的纵向气动特性;而横侧向气动特性值通常不作为选择准则。因此,这里仅针对纵向特性参数(轴向力系数、法向力系数和俯仰力矩系数)进行计算和对比分析。

表1 计算结果及比较
从表1可以发现,法向力系数CN、俯仰力矩系数Cm和相对压心pCFD与Datcom的计算吻合较好,误差在10%以内,满足工程估算精度要求;但轴向力系数CA有一定偏差,尤其在有舵偏的情况下偏差较大。
轴向力系数与导弹阻力密切相关。在工程计算中,导弹阻力一般分为零升阻力和诱导阻力两部分。对称外形的战术导弹和巡航靶弹零升阻力对应零攻角时总阻力;诱导阻力是指由于升力存在而增加的那部分阻力,与升力有密切关系,因此阻力计算是比较复杂的,这也是Datcom计算轴向力系数时出现误差较大的原因。CFD方法理论上可以直接对全弹进行N-S方程计算,从而得出较精确的阻力值,但此方法要求有较高的计算能力,成本较高。从工程经济效益考虑,此方法缺乏竞争力。Datcom在计算阻力时有较好的应用价值,但出现的偏差有待通过部件组合法逐项分析软件中各部分轴向力,再依据导弹外形做修正,从而找出更精确的计算方法。
3 结论
文中利用了某巡航靶弹的CFD计算数据和Datcom软件估算数据进行了比较,结果表明在一定范围内Datcom能够提供较高精度的估算值,基本满足初步设计的要求,具有一定工程应用价值。同时,Datcom避免了CFD软件计算周期长、建模复杂等缺点,大大节约导弹初步设计成本,对导弹初步设计及优化设计具有重要意义。部分精度不够的结果有待通过模型分析,发现不足之处再加以改进和完善。
[1]Blake W B.Missile datcom:user's manual[R].USAF Research Laboratory,Report AFRL2VA2WP2TR219982 3009,Wright-Patterson AFB,OH,3009,1998.
[2]Blake W B.Missile datcom:1997 status and future plans,AIAA-1997-2280[R].1997.
[3]James M Simon,William B Blake.Missile datcom:High angel of attack capabilities,AIAA-1999-4258[R].1999.
[4]William B Blake,Etan D Karni.A cambered body method for missile datcom,AIAA-2005-4971[R].2005.
[5]Eric J Abney,Melissa A McDanel.High angle of attack aerodynamic predictions using missile datcom,AIAA-2005-5086[R].2005.
[6]陈旭.近程反坦克导弹总体/控制一体化设计[D].西安:中国航天动力技术研究院,2010.
[7]纪楚群.导弹空气动力学[M].北京:宇航出版社,1996.
[8]杨维维,陈小前,李晓斌,等.通用导弹气动力计算软件DATCOM的开发与校验[J].固体火箭技术,2006,29(3):161-164.
