捷联惯导寻的导弹自动驾驶仪特性对气动力设计的约束*

李友年，陈星阳

(中国空空导弹研究院，河南洛阳 471009)

0 引言

为了有效拦截目标，寻的导弹自动驾驶仪必需满足制导的要求，具有足够的快速性和一定的阻尼，特别是在飞行过程中气动特性发生变化的时候，系统必须满足上述要求。而由于受到弹上设备、执行机构或其它因素的限制，自动驾驶仪无法允许弹体气动力特性随意变化，需要对其进行一定的约束，以保证寻的导弹能够有效拦截目标[1，4]。

对于没有捷联惯导的导弹，在飞行过程中无法得到迎角和侧滑角信息，因而无法根据弹体气动力特性随迎角和侧滑角的变化关系来调整控制增益，快速性和阻尼的要求又将约束这种变化的范围。对于带有捷联惯导的导弹，能够获得迎角和侧滑角信息，因而能够根据弹体气动力特性随迎角和侧滑角变化的关系来调整控制增益，相对于无捷联惯导的情况，约束又将发生变化[3]。

文中先给出了在无捷联惯导情况下，导弹自动驾驶仪特性对其俯仰通道两个稳定导数Mα和Mδ变化范围的约束，进而讨论了在有捷联惯导情况下，这种约束情况的变化。

1 导弹自动驾驶仪模型

文中导弹俯仰通道自动驾驶仪采用11阶模型[2]，其结构如图1 所示。

图中，导弹空气动力学传递函数如下式所示：

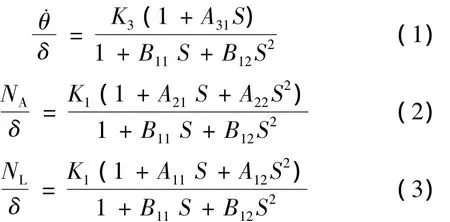
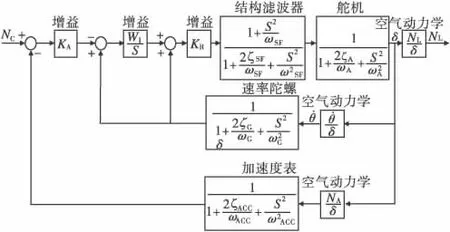
图1 自动驾驶仪模型

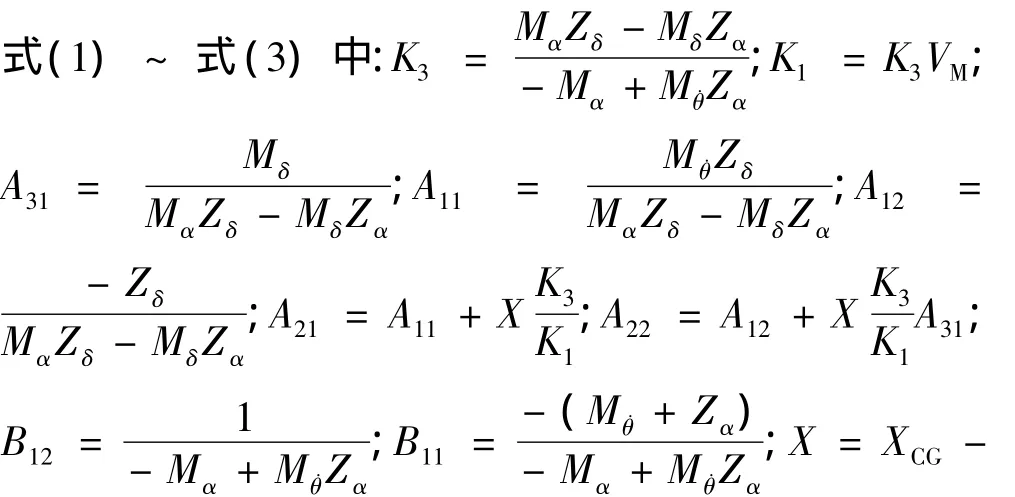
XACC;XCG为导弹质心位置;XACC为加速度表安装位置。

速率陀螺、加速度表和结构滤波器的参数取值如下：ωG=300rad/s;ζG=0.65;ωSF=314rad/s;ζSF=0.5;ωA=220rad/s;ζA=0.65;ωACC=300rad/s;ζACC=0.65。

为了使导弹飞行控制系统的响应满足所期望的要求，可以调整增益KR、KA和WI，考虑到结构滤波器、舵机、速率陀螺和加速度表的频带都比较高，在设计自动驾驶仪时可以不考虑它们的影响[5]，采用三阶模型进行简化，传递函数如下式：

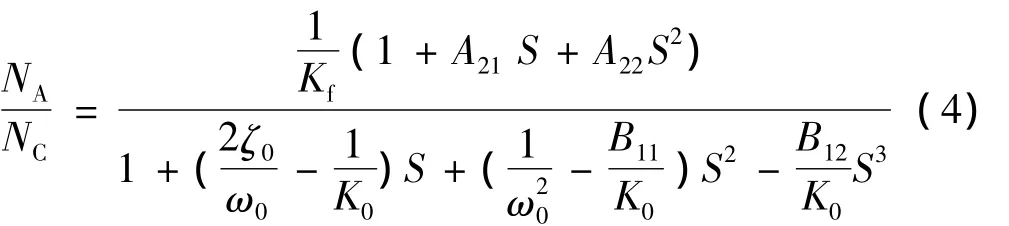
若闭环极点的特征值是一个实根和一对共轭复极点，则可以通过选择增益KR、KA和WI以获得所期望的闭环时间常数(τ)、闭环共轭复根的阻尼(ζ)和开环截止频率(ωCR)。式(4)中的系数由自动驾驶仪增益和弹体动力学特性表示，若按期望的闭环形式表示如下式。

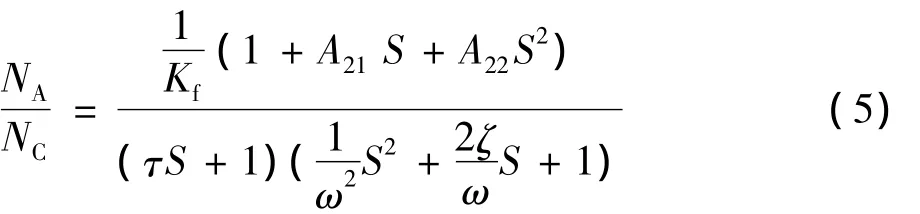
若令式(4)和式(5)对应的系数相等，则通过代数运算可以获得三个增益：

2 无捷联惯导自动驾驶仪特性对气动力的约束

对于没有捷联惯导的导弹，在飞行过程中无法得到迎角等信息，也就无法获知气动力随迎角的变化情况，因而在自动驾驶仪设计时，只能按照气动力的标称值设计一组控制增益，以容忍因迎角变化而带来气动力变化所造成的系统性能的差异。

文中假设导弹在滑行段时，其气动力参数的标称取值如下：M˙θ=－1.5/s;Mα=－250/s2;Mδ=－280/s2;Zα=－1.6/s;Zδ=－0.23/s;XCG=46 in;XACC=53.18 in。

若导弹的开环截止频率ωCR取44rad/s(从δ处断开)，并认为导弹闭环控制系统的时间常数τ取0.2，阻尼ζ取0.9是较好的性能，则利用式(6)～式(8)可以计算出在以上标称气动力参数情况下，自动驾驶仪的3个增益分别为：KR=0.163，WI=9.75，KA=0.00114。

这组增益即为在无捷联惯导情况下，依据已知的弹体气动特性以及自动驾驶仪性能指标所设计的标准增益。而随着Mδ的变化(其余气动力参数不变)，可以按此方法计算出每次Mδ变化后所对应的一系列标准增益值。如果固定每次Mδ变化后对应的标准增益值，并同时改变Mα的值，则闭环系统的性能(闭环系统阻尼ζ和时间常数τ)就会发生改变。

若设定闭环系统性能的边界，就能得出在给定Mδ的情况下，所能允许Mα的变化范围。

图2为在无捷联惯导的情况下，当设定闭环系统阻尼ζ不小于0.3，时间常数不大于0.7时，Mα和 Mδ之间的约束关系。

从图2中可以看出：在给定闭环系统性能边界的情况下，Mα取正值的边界受到闭环系统阻尼的限制，Mα取负值的边界受到闭环系统时间常数的限制。

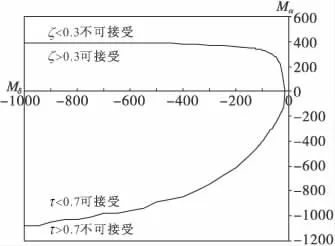
图2 Mα和Mδ之间的约束关系(无惯导)

3 带捷联惯导自动驾驶仪特性对气动力的约束

对于带有捷联惯导的导弹，在飞行过程中能够得到迎角等信息，因而可以推断气动力随迎角的变化情况。在自动驾驶仪设计时，可预先设定增益随迎角的变化，使得闭环系统能够应对因迎角变化所带来的弹体气动特性的变化，进而保持闭环系统性能的稳定。

假定导弹在滑行段时，其气动力参数的标称取值与上节相同。导弹的开环截止频率ωCR取44rad/s(从δ处断开)，并认为导弹闭环控制系统的时间常数τ取0.2，阻尼ζ取0.9是较好的性能。当Mδ发生变化时(其余气动力参数不变)，依然可根据式(6)～式(8)计算出相应的控制增益KR、WI和KA。

固定每次Mδ变化后的值，使Mα的值发生变化，并再次利用式(6)～式(8)计算出相应的控制增益，闭环系统的性能(闭环系统阻尼ζ和时间常数τ)会发生改变。

图3为在有捷联惯导的情况下，当设定闭环系统阻尼ζ不小于 0.3，时间常数不大于0.7时，Mα和Mδ之间的约束关系。

图3 Mα和Mδ之间的变化关系(有惯导)

从图3中可以看出：在有惯导情况下，Mα取值的边界依然受到闭环系统阻尼和时间常数的限制，但不再随Mδ变化，而且可接受的Mα取值范围也要比无惯导时的大。

4 仿真验证

在有捷联惯导的情况下，分别取下面两组气动力参数(质心位置 XCG=46in，惯导位置 XACC=53.18in)。

第一组参数为M˙θ=－1.5/s，Mα=600/s2，Mδ=－400/s2，Zα=－1.6/s，Zδ=－0.23/s。由第一组参数计算得控制增益 KR=0.11，WI=28.7，KA=0.0000116。

第二组参数为M˙θ=－1.5/s，Mα=－600/s2，Mδ=－800/s2，Zα=－1.6/s，Zδ=－0.23/s。由第二组参数计算得控制增益 KR=0.058，WI=2.31，KA=0.00735。

图4为按照图1所示结构，在不同参数下，闭环系统的阶跃响应。

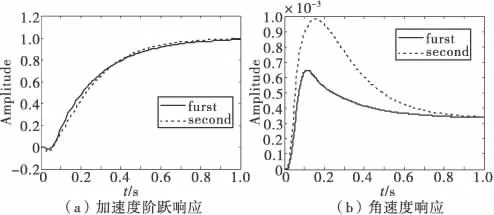
图4 闭环系统阶跃响应

从图4可以看出：对于上面两组参数，闭环系统的时间常数和阻尼能够满足性能要求，并与图3的结果相符合。

5 结论

在无捷联惯导的情况下，文中分析了导弹自动驾驶仪特性对气动力参数Mα随Mδ变化的约束条件及边界。在此基础上，又讨论了在有捷联惯导的情况下，导弹自动驾驶仪特性对气动力参数Mα的约束条件及边界。

通过对比看出：有捷联惯导时，Mα取值的边界依然受到闭环系统阻尼和时间常数的限制，但不再随Mδ变化，而且可接受的Mα取值范围要比无惯导时的大。

[1]F William Nesline，Mark L Nesline.How autopilot requirements constrain the aerodynamic design of homing missile[C]//American Control Conference，1984 Vol.2：716－730.

[2]Nesline F William，Nabbefeld Norman C.Design of digital autpilots for homing missiles[C]//Proceedings of AGARD Flight Mechanics Panel Symposium，1979 Vol.29：1－14.

[3]Garnell P，East D J.Guided weapon control systems[M].Pergamon Press，1977.

[4]Nesline F W，Zarchan P.Miss distance dynamics in homing missiles[C]//AIAA Guidance and Control Meeting，Seattle，Washington 1984.

[5]Ford J T.Missile Aerodynamics，System Simulation and A-nalysis[Z].Raytheon Company，1981.